基于分布分數圖對一元弱酸相關的滴定曲線的討論
李娜
北京大學化學與分子工程學院,北京 100871
分布分數圖是基于物料平衡原理與解離平衡表達式而繪制的,反映了體系中弱酸堿各相關物種的分布分數(濃度相對值)隨pH的變化,在復雜體系的平衡處理中是一個基本且重要的關系式。分布分數在計算溶液pH、不同酸堿型體的濃度、緩沖容量,以及滴定誤差等方面均有很好的應用[1–3]。本文基于分布分數對一元弱酸相關的滴定體系之滴定曲線進行討論,包括一元弱酸的滴定,以及強酸與一元弱酸混合酸的滴定。為不影響討論主線,本文略去一些基本pH計算以及誤差計算過程。
1 一元弱酸的滴定曲線
酸堿滴定曲線是pH–T%函數,其中T%為滴定分數。滴定分數為100% (化學計量點,SP)、99.9%(計量點前0.1%,?0.1% SP)和100.1% (計量點后0.1%,+0.1% SP)是滴定曲線上最重要的三點。滴定分數在從99.9%至100.1%變化時,pH發生突然的改變,稱為滴定突躍,pH變化范圍稱為滴定突躍范圍。下面以0.1 mol·L?1NaOH滴定Ka在10?2–10?7之間的同濃度一元弱酸HA為例,對滴定曲線進行討論。
強堿滴定一元弱酸的滴定分數:

式中:c(NaOH)為滴定劑NaOH的濃度,為0.1 mol·L?1,V(NaOH)為滴定過程中向弱酸溶液中加入0.1 mol·L?1NaOH的體積,ct(HA)為在任意V(NaOH)下,溶液中HA的總濃度,V(HA)為0.1 mol·L?1HA的起始體積。
計量點前,溶液組成為HA-A?,對于計量點前任意滴定分數T%,
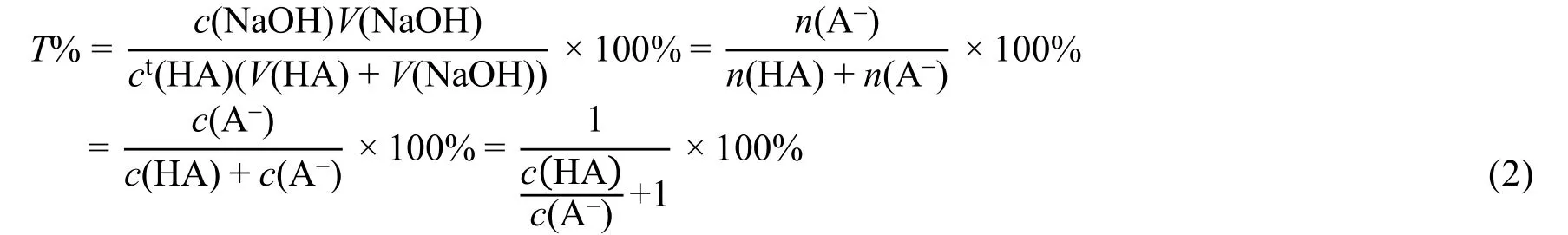
式中:n(HA)與n(A-)分別為HA與A-兩種形態的量,c(HA)與c(A-)分別為HA與A-的分析濃度。
對于一元弱酸HA,A-的分布分數為:

由物料平衡式和電荷守恒式可以導出[1,2]:

計算溶液[H+]的公式為:

根據溶液的酸堿性可以選擇使用:

或者,

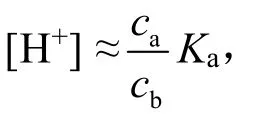

此時,x(A-) × 100%可以表示滴定分數。
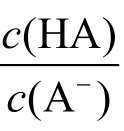
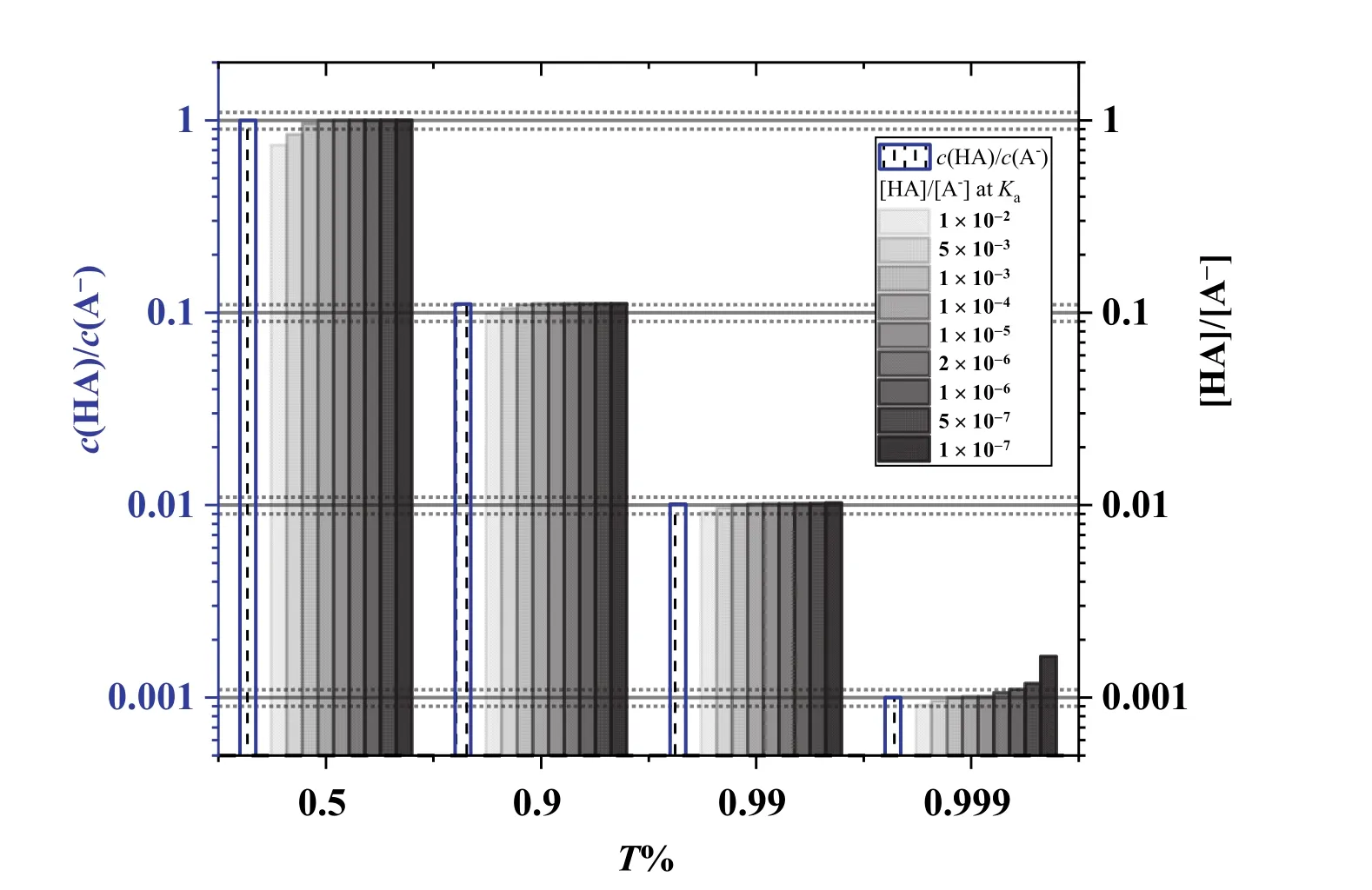
圖1 滴定分數為50%,90%,99%,及99.9%時,不同Ka值的HA的以及由近似式求算的
當Ka>2 × 10?6,T% = 100.1%的pH由過量的NaOH計算,pH = 9.7。
因此,以0.1 mol·L?1NaOH滴定Ka≥ 2 × 10?6的同濃度一元弱酸HA,從分布分數圖(圖2)可以直觀地看出來,滴定突躍范圍為(pKa+ 3) ? 9.7。對于常見的一元弱酸HAc,Ka= 10?4.76,滴定突躍范圍為pH 4.76–9.7。滴定突躍范圍隨著Ka增大而增大,Ka增大10倍,pH (?0.1% SP)向酸性pH擴展1 pH。Ka=2 × 10?6時,滴定突躍范圍為8.68–9.74,對應的[H+]濃度與最簡式結果相比,誤差為~5%,可以近似認為滴定突躍范圍為(pKa+ 3) –9.7,即8.7–9.7。
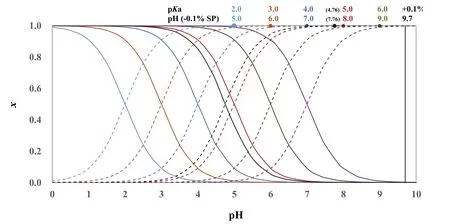
圖2 10?2.0,10?3.0,10?4.0,10?4.76,10?5.0,10?6.0和10?7.0的一元弱酸的分布分數圖
對于Ka為1 × 10?6的一元弱酸,計量點前0.1%的pH為8.96,對應的[H+]與最簡式計算結果相比,誤差~9%;計量點后0.1%時,質子條件式中[HA]與c(NaOH)相比不可忽略(c(NaOH) = 0.30[HA]),pH為9.77,與pH = 9.7相比,[H+]的誤差約為?15%。對于Ka為1 × 10?7的一元弱酸,同樣道理,無法使用最簡式從分布分數圖獲得滴定突躍范圍,由近似計算得滴定突躍范圍為9.70–10.00;假設可以選到正好在化學計量點的pH變色的指示劑,由于人眼觀測滴定終點有±0.3 pH單位的不確定性,終點范圍將是9.85 ± 0.3,即9.55–10.15,對應于±0.2%滴定誤差;此時若把濃度提高至10倍,即1 mol·L?1,雖然?0.1% SP的pH計算仍不能采用最簡式,但是滴定突躍為9.93–10.70,如果選擇恰好在化學計量點的pH變色的指示劑,終點范圍(10.35 ± 0.3)包含在滴定突躍范圍內,滴定誤差在±0.1%范圍。
下面討論分布分數對滴定誤差的影響。當弱酸的酸性不太強時,只能選擇弱堿性范圍變色的指示劑,如酚酞(PP),PP的變色點pH = 9.0。
0.1 mol·L?1NaOH滴定同濃度的HA,根據誤差定義,并經合理近似,可得:

式中:下標ep表示滴定終點,sp表示計量點,csp(HA) = 0.05 mol·L?1。
在以PP指示的滴定終點,pHep= 9.0,[OH-]ep= 104× [H+]ep,[H+]ep與[OH-]ep相比,可被忽略,式(10)簡化為:

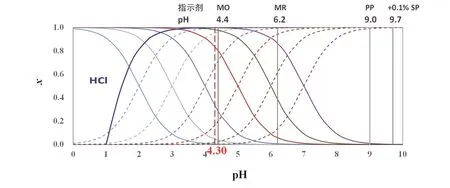
根據式(11),xep(HA)與E隨Ka的變化如表1所示。當HA的酸性較強時,離解度大,xep(HA)較小。當Ka≥ 5 × 10?5時,xep(HA) ≤ 10% × 10-3.7,忽略xep(HA),誤差主要受溶液中的[OH?]ep影響,E= 0.02%;若10% × 10?3.7 表1 0.1 mol·L?1 NaOH滴定同濃度HA的滴定誤差(PP指示劑,pHep = 9.0) 對于強堿滴定強酸和弱酸的混合溶液,以0.1 mol·L-1NaOH滴定同濃度的HCl和HA混合酸溶液(HA的Ka不同)為例進行討論。HCl滴定分數隨pH的變化,以及HA (不同Ka)的分布分數隨pH變化如圖3所示。 圖3 Ka為10?2.0,10?3.0,10?4.0,10?4.76,10?5.0,10?6.0和10?7.0的一元弱酸的分布分數圖,及以0.1 mol·L?1 NaOH滴定同濃度的HCl時滴定分數(T% / 10?2)隨pH變化 首先,我們來討論選擇性滴定HCl的可能性與條件。 以0.1 mol·L?1NaOH滴定同濃度HCl的突躍范圍為pH 4.3–9.7,在?0.1% SP,溶液的pH = 4.30。欲選擇滴定強酸和弱酸混合體系中的強酸,終點為弱酸HA體系,須需選擇酸性pH范圍變色的指示劑。 選擇滴定HCl時,根據誤差定義,經過合理近似,可得: 使用甲基橙作指示劑時,pHep= 4.4,則式(12)為: 如表2所示,當Ka在10?2.0–10?6.0范圍,xepA-≥ 30 × 10-3.1,E主要由xepA-貢獻,xepA-> 0.02,即有超過2%的HA參與反應,消耗NaOH,此時無法以不超過±0.1%的誤差選擇滴定其中的強酸HCl;當Ka= 10?7.0,xep(A-) = 3 × 10-3.1,xep(A?)與10?3.1的貢獻不能忽略,此時誤差由二者之差決定,誤差達到最小值,有0.2%的弱酸被滴定,此時滴定HCl的誤差為0.2%。當Ka為10?7.0時,滴定HCl完成后,如前節討論,可以繼續滴定Ka為10?7.0的弱酸。 若以甲基紅(MR)為指示劑,滴定終點pH為6.2,即使對于Ka為10?7.0的一元弱酸,也有13.7%的酸參與反應,無法實現選擇滴定HCl,也無法實現混合酸總量滴定。 對于Ka≥ 10?7.0的一元弱酸,無法選擇滴定HCl,但是可以滴定混合酸總量。原理如前節所述,在此不作詳細論述。滴定弱酸,需選擇在堿性范圍變色的指示劑,如酚酞,pHep= 9.0。 根據滴定總酸量的誤差定義,并作合理近似,得: 使用酚酞為指示劑時,滴定終點pH為9.0,式(14)近似為: 根據式(15),xep(HA)與E隨Ka的變化如表2所示。當HA的酸性較強時,離解度大,xep(HA)較小。合酸總量的誤差是0.1 mol·L?1NaOH滴定同濃度相同弱酸的一半。根據誤差定義,混合酸的總量是弱酸的2倍,這個結果也是合理的。 表2 0.1 mol·L-1 NaOH滴定同濃度的HCl與HA混合酸的滴定誤差 綜上,本文討論了直接通過分布分數獲得一元弱酸滴定突躍范圍的可行性以及分布分數滴定誤差的影響。由于分布分數受弱酸的Ka以及溶液的pH影響,因此必然影響滴定突躍范圍和滴定誤差,通過這些討論有助于深入理解酸堿平衡與酸堿滴定。
2 強酸和一元弱酸混合溶液的滴定曲線
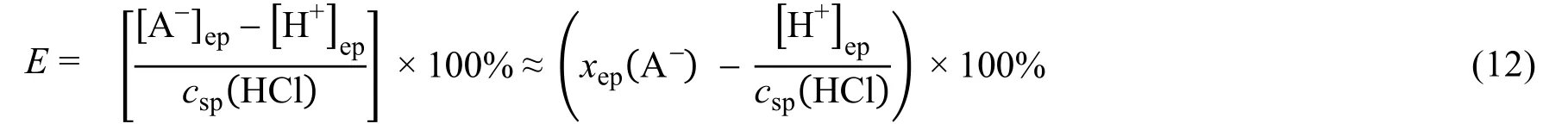





3 結語

