化學分析測量數據處理有關概念的相關商榷

岳宣峰，樊鑫，秦丹，逯昊文，張延妮

1陜西師范大學化學化工學院，陜西省生命分析化學重點實驗室，西安 710062

2陜西師范大學藥用資源與天然藥物化學教育部重點實驗室，西安 710062

1 引言

為了對測量數據進行科學的處理，現行《化學分析》教材中普遍介紹了相關化學計量學基礎知識，并將其應用于對真值的預期。化學測量的基礎理論是化學計量學，它通過數學及統計學方法在研究對象的“表觀狀態”和“真實狀態”之間建立聯系，并通過解析測量數據最大限度地提取被研究對象的有關特征信息。因此，教材中普遍介紹了誤差、絕對誤差、相對誤差、系統誤差、隨機誤差、偏差、準確度、精密度等概念，并對這些概念之間的關聯也做了一定解讀，這些內容涉及化學測量、統計學、數學及語言邏輯等多個學科，給教材的編寫帶來了很大的挑戰，現行主要《化學分析》教材[1,2]在涉及以上知識的編排結構上還不甚合理，一些概念的定義還不夠統一，一些概念的分類還不夠清晰，還有一些知識存在可能的疏漏甚至錯訛，而這些問題都是分析化學專業共同體進行理論研究和教育教學時亟待解決的問題。本文基于概念的分類規則和定義規則，對兩本主要《化學分析》教材中涉及測量數據處理的概念進行了探討，指出有關概念的命名、定義、分類、知識編排等方面存在的問題，并提出了相應的改進建議。

2 概念的分類和概念的定義

2.1 概念分類的屬性及其對概念定義的內在要求

概念分類是一項復雜的工程，涉及所有學科，并且需要在一定的哲學觀念的指導下進行。相對于具體學科，跨學科的概念分類就更為困難，一方面是由于綜合性工程的巨大挑戰，另一方面是眾口難調，要取得一致的分類標準非常困難；另外，哲學思想對這項工程起著綱領性的作用，而至今真正取得不同階層、不同民族、不同國家與文明社會認同的作為科學的哲學還沒有出現。因此，那種全面統一的概念分類及其體系的實現還有一段相當長的道路要走，但這并不妨礙在同一學科內部及交叉學科之間不斷對舊概念進行新分類的嘗試，甚至創立新概念。構建基礎概念類別應該以語言學、形式邏輯、辨證邏輯、數學、系統論等學科所涉及的廣義對象為基點，有關概念分類及構建的注意事項及其與專業術語之間的關聯關系見文獻[3]。概念分類的外延研究要求首先明確概念的定義，定義的合理描述有助于聚焦概念最關心的關系脈絡，從而提高概念運用的效率。

2.2 概念的兩種定義方法

在教育研究中，當在不同的層面、從不同的角度、用不同的定義來探討同一個概念時，往往會產生很多誤解和歧義，很大一部分原因是由于對所探討的概念沒有明確客觀的操作性定義造成的。所謂概念的操作性定義(operational definition)是根據可觀察、可測量、可操作的特征來界定概念含義的方法，從本質上說，下操作性定義就是詳細描述研究變量的操作程序和測量指標，美國的物理學家布里奇的這一觀點和思想在1971年被美國的《科學》雜志列為世界五大哲學成就之一，他認為：科學上的概念如果要想避免曖昧不清，最好能以我們“所采用的測量它的操作方法”來界定。下操作性定義的方法、注意事項等見文獻[4]。所有的實證性研究都必須有測量，并且所有的測量都必須把一般的抽象概念變為具體的行為指標，以便他人重復、驗證和交流，因而在實際研究過程中，操作性定義和抽象性定義都是需要的，應根據研究的性質和目的靈活運用。在給概念下定義的過程中，抽象性定義可涵蓋研究概念所屬的基本特征，解釋范圍較大，具有普遍性，但往往失之籠統，無法據此測量和操縱研究的概念；操作性定義著眼概念的客觀可檢驗性，對概念的界定清楚明確，便于操縱和測量，但往往只能涉及概念的少數特征，具有明顯的排它性；當一個概念同時具有兩個定義時，比較理想的方式是：先用抽象性定義描述概念的基本特征，然后再用操作性定義描述概念的操作程序和測量指標，前者為后者提供方向并指明意義。

3 《化學分析》教材中測量數據處理有關概念的相關商榷

按照以上的概念分類和概念定義規則，對現行兩本主要《化學分析》教材中與測量數據處理有關的概念及相關內容展開商榷，涉及預期真值的方法、準確度的內涵及其與誤差的關系、誤差的抽象性定義、誤差的操作性定義及分類、誤差的構成、測量的正確性及其判斷方法、數值的“精密度”及衡量指標、預期真值的區間表達法等，詳細內容如下。

3.1 預期真值的方法

現狀：教材中有準確度、誤差、置信度和置信區間等概念的介紹，但沒有預期真值方法的明確分類[1,2]。

商榷：以上幾個概念之間的關聯關系不夠明晰(比如：真值→預期值→準確度→誤差，這些概念引入教材時未能做好環環相扣)，各個概念適用的領域并未完全明確(比如：準確度可以用來評價平均值法預期真值的效果，但一般不用于評價區間法預期真值的效果)，涉及的內容在編排上不夠緊湊(將這些概念有機統一起來的起點是：對真值的預期這個目的，然后是預期方法的分類，最后是對這些預期方法效果的評價指標，這些內容在現有教材中并未按照這一邏輯編排)，知識結構呼應性不夠強(“準確度”和“誤差”涉及到真值，而“置信度”和“置信區間”只涉及總體平均值，其實這些概念的展開始終都應該和測量工作的根本目的即預期真值要相呼應)。

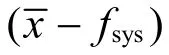
3.2 準確度的內涵及其與誤差的關系

現狀：準確度是指“測量值與真值的接近程度，用誤差來衡量”[1]或“分析結果與真值的相符程度，通常用誤差來表示”[2]。誤差越小，準確度越高；誤差越大，準確度越低[1,2]。

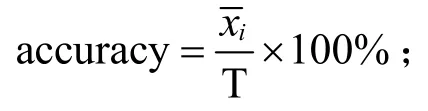
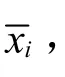
3.3 誤差的抽象性定義

現狀：對于概念“誤差”，教材中并未提供確切的抽象性定義[1,2]。

商榷：相對于“絕對誤差”及“相對誤差”這些低一級的概念，“誤差”這個處于分類體系上一級的概念尚無抽象性定義，顯然有待補充。

建議：誤差指的是研究對象某性質的真實狀況與其預期狀況之間的差別。

3.4 誤差的操作性定義及分類

商榷：“兩種表示方法”暗含“兩種方法的主體是相同的，不同僅存在于外在的表示形式”，然而“絕對誤差”和“相對誤差”卻著眼于不同的角度，在內容和形式上都有差別，因此表述“誤差有兩種表示方法”有誤；表述“誤差可用絕對誤差和相對誤差來表示”既有概念分類的錯誤又有語意表達的錯誤。不同教材中絕對誤差的可操作性定義本質相同，然而表達式中的符號并不統一，對應的抽象性描述也不夠統一，將“分析結果”和“測量值”統一改為“預期值”更為合理；類似的問題也存在于兩本不同教材[1,2]對“相對誤差”的描述中，另外，描述的語言在語法及用語上也都有錯誤。

建議：科學上常用一個數值表示研究對象某性質的具體狀態，“誤差”定義中的兩個狀態對應的兩個值分別稱為真值(T)和預期值()，對于這兩個值的差別，按照關注角度是絕對還是相對的差異，分為絕對誤差和相對誤差，前者(absolute error)用Eab表示，其表達式為后者(relative error)用Ere表示，其表達式為

3.5 誤差的構成

現狀：按照來源和性質的不同，誤差分為系統誤差和隨機誤差[1,2]。系統誤差是由某種固定的原因造成的，具有重復性、單向性，又稱可測誤差。隨機誤差是由某些難以控制且無法避免的偶然因素造成的，大小和正負不定，無法測量、不可避免且無法校正，大量平行測量的隨機誤差服從正態分布，且“用-μ表示”[1,2]。

商榷：如果按照教材[1,2]中的命名及分類原則，“系統誤差”和“隨機誤差”屬于“誤差”的子級概念，那么其應具有母級概念的本質特征(預期值與真值的差別)，然而“隨機誤差”與真值無關，“系統誤差”與預期值無關，顯然，這里存在子級概念外延逾越母級概念的錯誤。另外，“系統誤差”尚無可操性定義；“隨機誤差”的抽象性定義和可操性定義不是聯袂呈現的，不利于認知的合理建構。

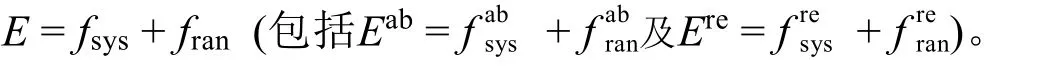
按照絕對誤差的定義：

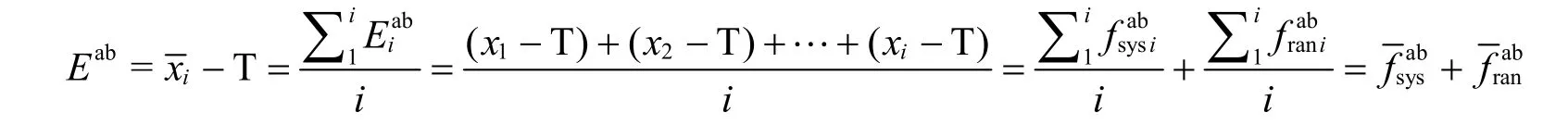
3.6 測量的正確性及其判斷方法

現狀：無測量的正確性這一概念[1,2]。

商榷：眾所周知，測量的重現性高是其準確度高的必要而不充分條件，那么是測量的哪個環節的缺失導致了這個“不充分”呢？是正確性！

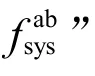
3.7 數值的“精密度”及衡量指標

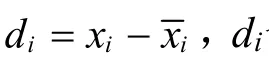
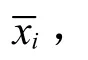
3.8 預期真值的區間表達法

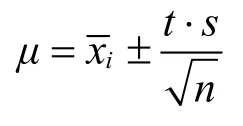
商榷：測量的目的是為了預期真值，預期真值時的誤差等于系統項fsys加上隨機項fran，系統項是固定值，隨機項出現的規律符合正態分布或者t分布，可以在計算總體平均值μ的基礎上再考慮誤差的系統項，就可以直接預期真值T所屬的區間。另外，目前教材中給出的總體平均值μ的置信區間只是各種可能性中的一種，它是在保證優先考慮數值精密性最好的前提下的置信區間，有關這一點我們會另撰文闡述。