依據(jù)BP神經(jīng)網(wǎng)絡(luò)的機(jī)載LiDAR數(shù)據(jù)估算林分平均高1)

周蓉 趙天忠 吳發(fā)云

(北京林業(yè)大學(xué)，北京，100083) (國(guó)家林業(yè)和草原局調(diào)查規(guī)劃設(shè)計(jì)院)

激光雷達(dá)(LiDAR)是通過激光掃描儀發(fā)射的激光脈沖測(cè)定發(fā)射器與目標(biāo)物之間的距離的一種主動(dòng)式遙感技術(shù)。由于激光脈沖對(duì)森林冠層的穿透性，LiDAR技術(shù)被廣泛應(yīng)用于森林結(jié)構(gòu)參數(shù)獲取。林分平均高不僅是評(píng)價(jià)森林生產(chǎn)力、反映林木的生長(zhǎng)狀況、判斷林分立地質(zhì)量的重要指標(biāo)，也是反演森林生物量及蓄積量、研究森林碳儲(chǔ)量等其他森林參數(shù)的基礎(chǔ)[1-3]。

以機(jī)載激光雷達(dá)為技術(shù)依托，結(jié)合機(jī)載LiDAR點(diǎn)云數(shù)據(jù)和樣地實(shí)測(cè)數(shù)據(jù)對(duì)林分參數(shù)進(jìn)行估測(cè)已取得大量的研究進(jìn)展，從點(diǎn)云數(shù)據(jù)中提取相關(guān)特征參數(shù)對(duì)林分平均高估測(cè)，是目前基于LiDAR技術(shù)獲取森林樹高的研究熱點(diǎn)。ERIK et al.[4]提出基于樣地尺度的點(diǎn)云數(shù)據(jù)，提取不同分位數(shù)上的高度和密度變量，并以此構(gòu)建各種林分因子的線性回歸模型；焦義濤[5]、龐勇[6]、尤號(hào)田[7]、穆喜云[8]、顧海波等[9]基于高程歸一化的樣方內(nèi)植被點(diǎn)云數(shù)據(jù)，分別構(gòu)建了以植被點(diǎn)云高度閾值平均值、上四分位數(shù)處高度值、90%分位高度值、75%分位高度值、高度變量與強(qiáng)度變量多變量組合為自變量的林分平均高樹高線性回歸模型，實(shí)驗(yàn)結(jié)果均表明模型對(duì)林分平均樹高的估測(cè)有較好的表現(xiàn)，且不同的樹種之間表現(xiàn)形式有一定的差異性。

雖然線性回歸模型具有簡(jiǎn)單易懂的優(yōu)點(diǎn)，但要求樣本數(shù)據(jù)滿足正態(tài)性、獨(dú)立性等一定的假設(shè)限制，而實(shí)際數(shù)據(jù)往往難以滿足上述假設(shè)條件，同時(shí)線性回歸法也不能全面的解釋各數(shù)據(jù)之間的關(guān)系，因此將非參數(shù)的估測(cè)方法引入森林結(jié)構(gòu)參數(shù)反演中[10-11]。魯林等[12]基于機(jī)載雷達(dá)點(diǎn)云數(shù)據(jù)提取了高度分位數(shù)變量及點(diǎn)云統(tǒng)計(jì)特征值等變量，結(jié)合實(shí)測(cè)林分平均高數(shù)據(jù)，驗(yàn)證了隨機(jī)森林模型估測(cè)林分平均樹高的可靠性；LEE et al.[13]采用3種機(jī)器學(xué)習(xí)算法—SVR、RF、RT分別建立了林分平均高模型，試驗(yàn)表明3種機(jī)器學(xué)習(xí)都能適用于崎嶇地形和樹木種類復(fù)雜的森林；ALBERTO et al.[14]以巴西的火炬松為研究對(duì)象，結(jié)合機(jī)載LiDAR點(diǎn)云數(shù)據(jù)與地面實(shí)測(cè)數(shù)據(jù)，采用K鄰近法構(gòu)建了林分平均高及優(yōu)勢(shì)高的回歸模型，模型估測(cè)精度均在90%以上；TOMPALSKI et al.[15]為了驗(yàn)證模型的通用性及可轉(zhuǎn)移性，基于不同點(diǎn)云特征變量，分別采用線性回歸、隨機(jī)森林、KNN 3種算法構(gòu)建了不同區(qū)域的斷面積加權(quán)平均高模型；趙勛等[16]采用隨機(jī)森林回歸和支持向量機(jī)回歸兩種機(jī)器學(xué)習(xí)方法，建立了廣西壯族自治等區(qū)高峰林場(chǎng)實(shí)驗(yàn)區(qū)的隨機(jī)森林平均高模型、支持向量機(jī)平均高模型、隨機(jī)森林+支持向量機(jī)平均高模型，結(jié)果表明兩種機(jī)器學(xué)習(xí)方法結(jié)合的組合模型對(duì)數(shù)據(jù)的泛化及預(yù)測(cè)能力最佳；郝紅科[17]基于歸一化點(diǎn)云數(shù)據(jù)中提取的43個(gè)變量，分別采用逐步回歸法、支持向量機(jī)、快速人工神經(jīng)網(wǎng)絡(luò)方法，構(gòu)建了林分平均高模型，結(jié)果表明機(jī)器學(xué)習(xí)算法的模型精度均優(yōu)于線性模型；MONNET et al.[18]對(duì)比了支持向量機(jī)和最小二乘法之間的差異性，實(shí)驗(yàn)結(jié)果表明，支持向量機(jī)方法構(gòu)建的林分優(yōu)勢(shì)高模型精度更佳。因此，以機(jī)載LiDAR點(diǎn)云數(shù)據(jù)為基礎(chǔ)，進(jìn)行森林平均高的反演具有一定的可行性，且機(jī)器學(xué)習(xí)方法能夠在一定程度上彌補(bǔ)傳統(tǒng)回歸方法帶來的不足，更好地挖掘多種點(diǎn)云特征變量之間的關(guān)系，為森林參數(shù)的進(jìn)一步探究提供了研究思路。

但這些研究均直接采用斷面積加權(quán)法得到的林分平均高作為樣地實(shí)測(cè)平均高，未設(shè)置參照組對(duì)比分析；且忽略了同一種機(jī)器學(xué)習(xí)算法之間不同訓(xùn)練函數(shù)的差異性。綜上所述，本研究以東北虎豹國(guó)家公園北部區(qū)域?yàn)檠芯繀^(qū)，分析林分加權(quán)平均高和林分算術(shù)平均高之間的差異性，在對(duì)比傳統(tǒng)線性回歸方法與機(jī)器學(xué)習(xí)算法之間優(yōu)劣性的基礎(chǔ)上，研究分析同一種機(jī)器學(xué)習(xí)算法中不同訓(xùn)練函數(shù)之間的差異性，以此探討不同算法在機(jī)載LiDAR點(diǎn)云數(shù)據(jù)反演林分平均高模型中的適用性。

1 研究區(qū)概況

本文以東北虎豹國(guó)家公園范圍內(nèi)針葉純林為研究對(duì)象，東北虎豹國(guó)家公園跨吉林、黑龍江兩省，東起吉林琿春林業(yè)局青龍臺(tái)林場(chǎng)，西至吉林省汪清縣林業(yè)局南溝林場(chǎng)，南自吉林省琿春林業(yè)局敬信林場(chǎng)，北到黑龍江省東京城林業(yè)局奮斗林場(chǎng)，總面積共計(jì)146.12萬hm2，其中森林面積130.66萬hm2，森林覆蓋率達(dá)89.42%，森林蓄積量1.6億m3。研究主要范圍為大興溝、天橋嶺、穆棱、東京城4個(gè)林業(yè)局及地方林場(chǎng)(43°20′～44°3′N，129°20′～129°55′E)，氣候?qū)俅箨憹駶?rùn)性季風(fēng)氣候，地貌多為山地，年平均氣溫4 ℃，降水量400～800 mm，受海洋氣候影響，環(huán)境濕潤(rùn)水系發(fā)達(dá)。植被類型屬長(zhǎng)白山植物區(qū)系老爺嶺亞區(qū)，基本林分類型為溫帶針闊葉混交林，有野生植物約3 890種，其中主要樹種為紅松(Pinuskoraiensis)、云杉(Piceaasperata)、落葉松(Larixgmelini)、椴樹(TiliatuanSzyszyl)、楊樹(Populus)等。

2 研究數(shù)據(jù)

2.1 機(jī)載LiDAR數(shù)據(jù)獲取及預(yù)處理

2018年9月，采用搭載RIEGL VQ-1560i機(jī)載三維掃描系統(tǒng)獲取LiDAR數(shù)據(jù)，飛行實(shí)驗(yàn)于晴朗、無云、無風(fēng)的日期開展，根據(jù)研究區(qū)的地形起伏將整個(gè)攝區(qū)分為2個(gè)區(qū)域，飛行絕對(duì)航高分別為2 300、2 100 m，最大激光脈沖頻率為1 000 kHz，最大掃描頻率為207 Hz。整個(gè)飛行過程的旁向重疊度控制在21%左右，點(diǎn)云密度約為4個(gè)/m2。

本文以LiDAR 360軟件為數(shù)據(jù)處理平臺(tái)，對(duì)點(diǎn)云數(shù)據(jù)進(jìn)行去噪、地面點(diǎn)分類、植被點(diǎn)分類等預(yù)處理工作，如圖1所示為預(yù)處理后樣地尺度的點(diǎn)云數(shù)據(jù)三維效果圖。從預(yù)處理的點(diǎn)云數(shù)據(jù)中提取與點(diǎn)云高程值相關(guān)的統(tǒng)計(jì)變量，如表1所示為提取的32個(gè)垂直結(jié)構(gòu)特征變量，包括22個(gè)高度相關(guān)統(tǒng)計(jì)變量和10個(gè)點(diǎn)云密度相關(guān)統(tǒng)計(jì)變量。

2.2 地面調(diào)查數(shù)據(jù)獲取及預(yù)處理

地面調(diào)查實(shí)驗(yàn)于2018年9月開展，在研究區(qū)內(nèi)分別設(shè)置32塊冷杉樣地、43塊云杉樣地、53塊落葉松樣地，共計(jì)128個(gè)純林樣地。首先觀察周圍林分狀況，確定圓形樣地的中心點(diǎn)，采集中心點(diǎn)GPS處坐標(biāo)，并記錄樣地的基礎(chǔ)信息；其次在設(shè)置的半徑為15 m，面積為0.07 hm2的圓形樣地內(nèi)進(jìn)行每木檢尺，獲取單木的胸徑、樹高、枝下高、冠幅等測(cè)樹因子，采用胸徑尺獲取每株單木1.3 m處的胸徑，采用VL5激光超聲波測(cè)高測(cè)距儀獲得了每木樹高、枝下高信息，采用皮尺測(cè)量獲得了樹木的東西、南北冠幅信息；最后通過差分GPS解算獲得樣木坐標(biāo)。樣地實(shí)測(cè)樣木信息統(tǒng)計(jì)如表2所示。

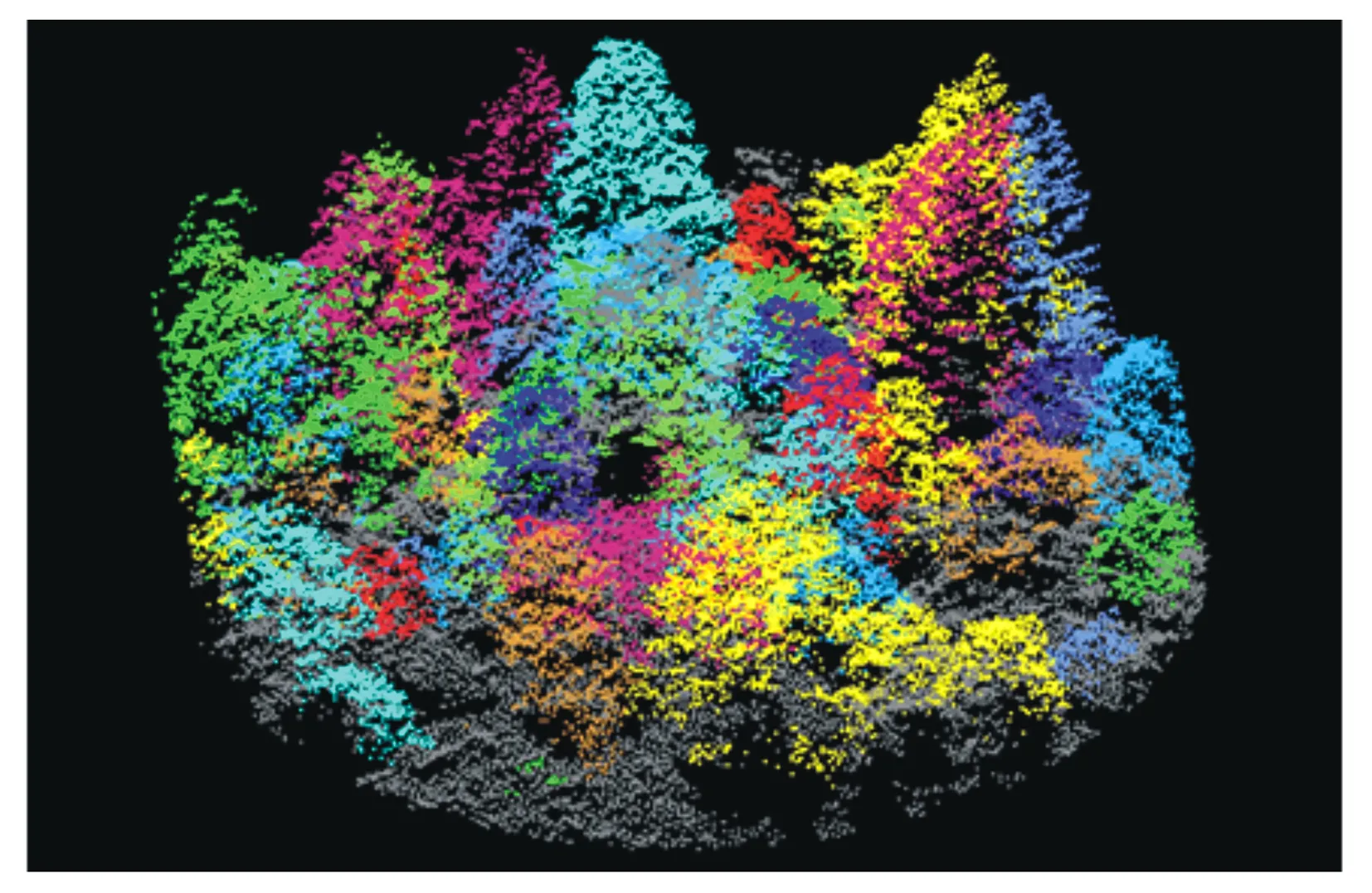
圖1 預(yù)處理后樣地點(diǎn)云數(shù)據(jù)效果

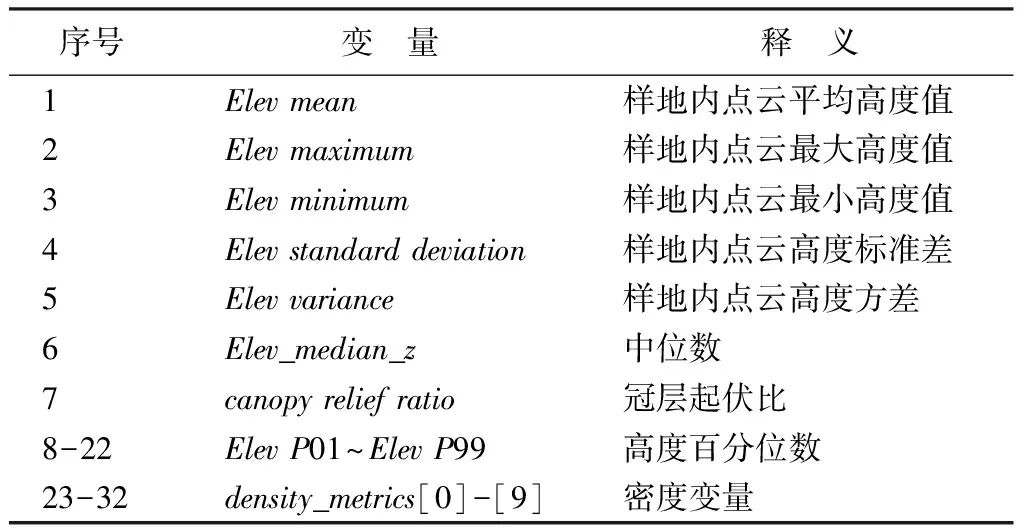
表1 32個(gè)點(diǎn)云特征變量統(tǒng)計(jì)

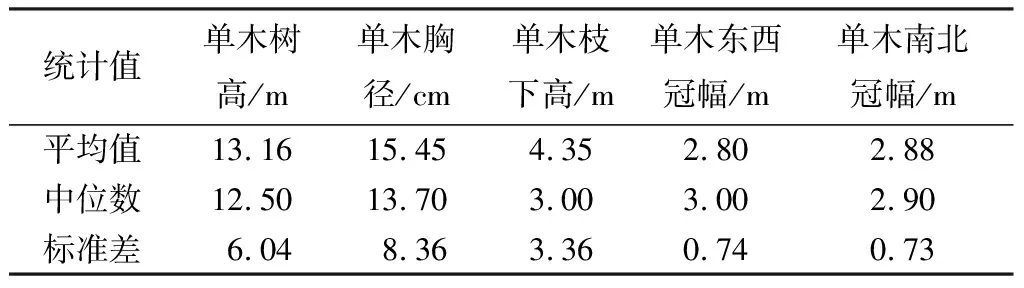
表2 樣木調(diào)查因子統(tǒng)計(jì)

本文擬探究各樣地的算術(shù)平均高、加權(quán)平均高之間的差異性是否會(huì)影響林分平均高反演模型的估測(cè)精度。根據(jù)公式(1)計(jì)算得各樣地算術(shù)平均高，林分加權(quán)平均高采用胸高斷面積加權(quán)法計(jì)算得到，計(jì)算公式如公式(2)所示。

(1)

(2)

式中：Ha為算術(shù)平均樹高；Hd為加權(quán)平均高；hi為第i株立木的樹高；Gi為第i株立木胸高斷面積；n為樣地內(nèi)的立木總數(shù)。

3 研究方法

3.1 基于機(jī)載LiDAR估測(cè)林分平均高基本原理

LiDAR系統(tǒng)通過激光掃描儀發(fā)射激光脈沖，測(cè)量主波射出與地面采樣點(diǎn)激光回波脈沖之間的時(shí)間間隔ΔT[19]，根據(jù)公式(3)可測(cè)算地表各點(diǎn)距傳感器發(fā)射點(diǎn)之間的距離，并通過LiDAR系統(tǒng)自身的GPS信息確定目標(biāo)物的三維坐標(biāo)信息。當(dāng)搭載激光雷達(dá)系統(tǒng)的有人機(jī)在森林上空作業(yè)時(shí)，激光雷達(dá)系統(tǒng)發(fā)射的脈沖信號(hào)穿透植被冠層，并接收森林樹冠層、樹干、地表等地面物反射的激光能量，通過計(jì)算地面和樹冠頂部的激光回波的距離即能獲得樹高[12，20-21]。

(3)

式中：L為傳感器與目標(biāo)物之間的距離；C為光速；ΔT為發(fā)射主波從傳感器到目標(biāo)物的往返傳輸時(shí)間。

3.2 逐步回歸模型構(gòu)建

本研究基于SPSS平臺(tái)開展逐步回歸模型的構(gòu)建，隨機(jī)選擇104個(gè)樣本數(shù)據(jù)進(jìn)行模型的構(gòu)建，剩余24個(gè)樣本數(shù)據(jù)作為測(cè)試樣本驗(yàn)證模型精度。根據(jù)逐步回歸算法的數(shù)學(xué)特性，分別優(yōu)選了不同的變量參與林分算術(shù)平均高、林分加權(quán)平均高模型反演研究，如表3所示，給出了優(yōu)選后參與模型構(gòu)建的變量及具體釋義。

表3 優(yōu)選后參與逐步回歸模型構(gòu)建的因子

3.3 BP神經(jīng)網(wǎng)絡(luò)構(gòu)建模型

BP神經(jīng)網(wǎng)絡(luò)是一種誤差逆向傳播的多層前饋神經(jīng)網(wǎng)絡(luò)，由輸入層、隱含層、輸出層構(gòu)成，本研究中BP神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)圖如圖2所示。分別采用貝葉斯正則化算法和L-M算法對(duì)BP神經(jīng)網(wǎng)絡(luò)進(jìn)行訓(xùn)練，L-M算法使得模型在具有全局收斂性的同時(shí)也具有局部收斂性[22-24]；貝葉斯正則化訓(xùn)練算法能夠有效改善擬合曲線的誤差[25-28]。具體的模型構(gòu)建過程如下：

(1)數(shù)據(jù)劃分及歸一化。本文引入驗(yàn)證樣本數(shù)據(jù)對(duì)模型構(gòu)建過程中的參數(shù)進(jìn)行調(diào)整，訓(xùn)練樣本∶驗(yàn)證樣本∶測(cè)試樣本為6∶2∶2。為了避免數(shù)據(jù)偏移分布帶來的無法收斂，采用mapminmax函數(shù)對(duì)輸入因子和輸出因子進(jìn)行歸一化處理，將數(shù)據(jù)分布映射到[-1,1]區(qū)間。

(2)網(wǎng)絡(luò)結(jié)構(gòu)確定。輸入層節(jié)點(diǎn)為32，輸出層節(jié)點(diǎn)數(shù)為1，根據(jù)公式(4)確認(rèn)隱含層范圍為7～16，確認(rèn)當(dāng)隱含層數(shù)為7時(shí)，模型擬合效果最佳，因此確認(rèn)BP神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu)為32∶7∶1。

(4)

其中：S為隱含層節(jié)點(diǎn)數(shù);n為輸入層的節(jié)點(diǎn)數(shù);o為輸出層節(jié)點(diǎn)數(shù);m為1～10之間任意整數(shù)。

(3)傳遞函數(shù)及參數(shù)確定。設(shè)置tansing函數(shù)作為隱含層的傳遞函數(shù)，以線性傳遞函數(shù)作為輸出層的傳遞函數(shù)；設(shè)置學(xué)習(xí)速率為0.01，最大迭代次數(shù)為1 000，目標(biāo)精度為0.001，最大驗(yàn)證失敗次數(shù)為10次。

3.4 模型評(píng)價(jià)標(biāo)準(zhǔn)

為了便于直觀分析模型的精度，采用R2決定系數(shù)、P樹高估測(cè)精度[5-8，12]作為本研究的模型精度評(píng)價(jià)指標(biāo)，具體計(jì)算方法見公式(5)、(6)。

(5)

(6)

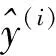
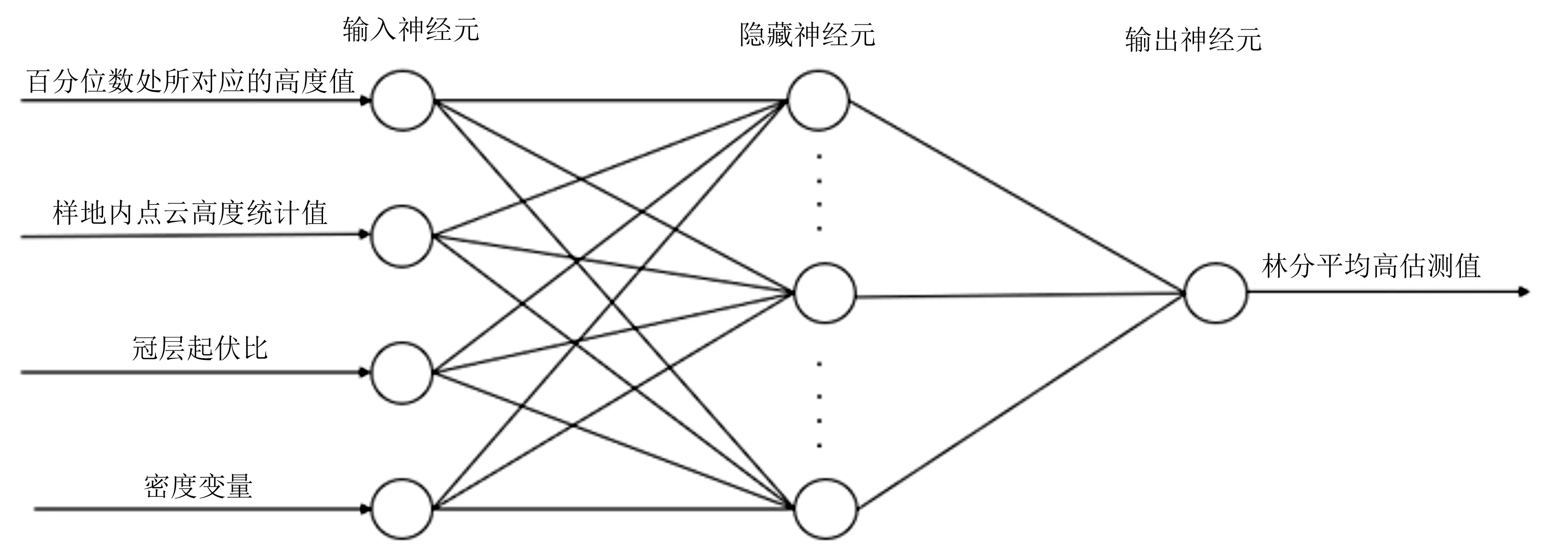
圖2 BP神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)圖

4 結(jié)果與分析

4.1 逐步回歸模型

當(dāng)采用24個(gè)檢驗(yàn)樣本數(shù)據(jù)驗(yàn)證逐步回歸法構(gòu)建的林分平均高估測(cè)模型精度時(shí)，各模型的估測(cè)值與實(shí)測(cè)值相關(guān)關(guān)系如圖3所示。

其中林分算術(shù)平均高模型，以單變量elev_median_z為自變量，圖3(a)表示了該模型估測(cè)的林分算術(shù)平均高與實(shí)測(cè)算術(shù)平均高的相關(guān)關(guān)系，其決定系數(shù)R2為0.809，具體表達(dá)式為：

Ha=3.201+0.847×Elev_median_z。

林分加權(quán)平均高模型是以ElevP70、density_metrics[4]為自變量構(gòu)建的，圖3(b)為模型的估測(cè)值與實(shí)測(cè)值的相關(guān)關(guān)系，決定系數(shù)R2為0.858，具體表達(dá)式為：

Hd=1.884+0.819×ElevP70+1.125×density_metrics[4]。

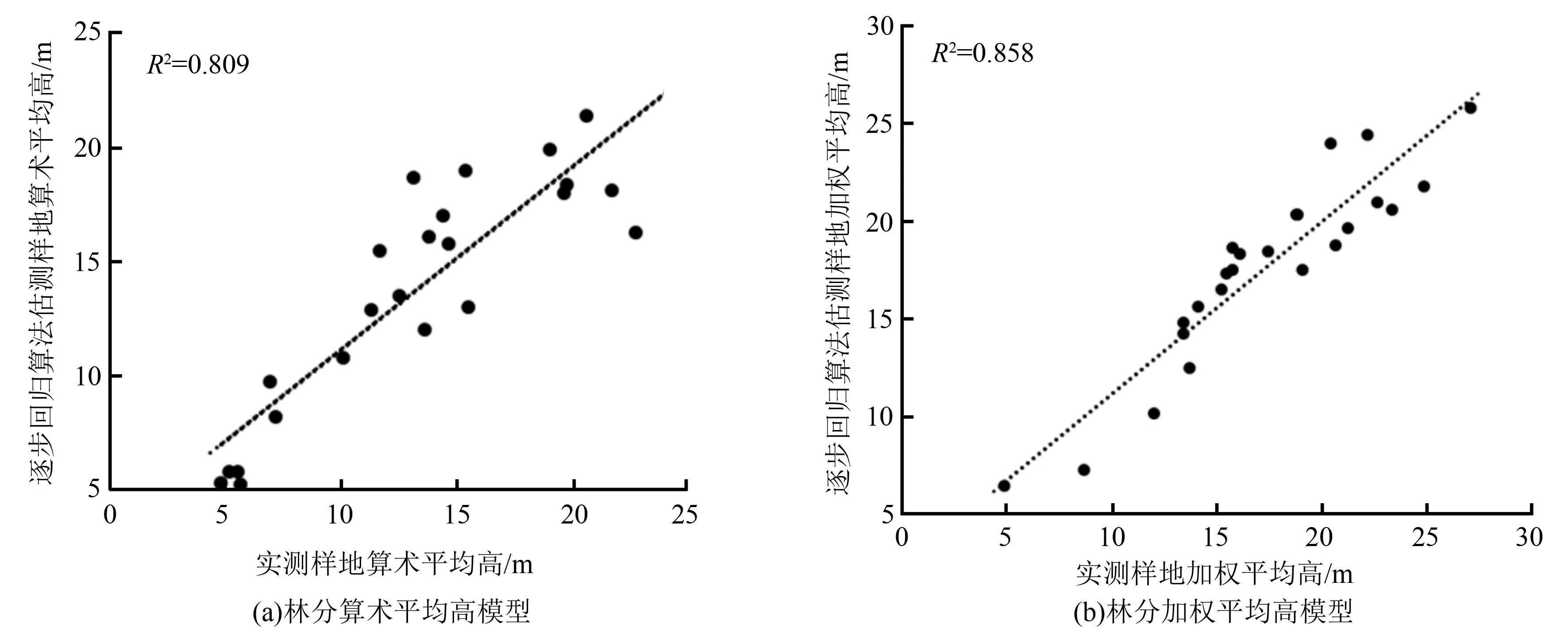
圖3 基于逐步回歸法估測(cè)的林分平均高與實(shí)測(cè)樹高對(duì)比圖

4.2 BP神經(jīng)網(wǎng)絡(luò)模型

根據(jù)獲取的BP神經(jīng)網(wǎng)絡(luò)模型，分別對(duì)樣地算術(shù)平均高、樣地加權(quán)平均高進(jìn)行預(yù)測(cè)。為檢驗(yàn)?zāi)Ｐ偷念A(yù)測(cè)精度，采用24個(gè)檢驗(yàn)樣本數(shù)據(jù)進(jìn)行平均高的估測(cè)，并分析了估測(cè)值與實(shí)測(cè)值的相關(guān)關(guān)系。圖4為基于L-M算法構(gòu)建的林分平均高模型的估測(cè)值與實(shí)測(cè)值的相關(guān)關(guān)系，其中圖4(a)為林分算術(shù)平均高模型，其決定系數(shù)為0.882；圖4(b)為林分加權(quán)平均高模型，其決定系數(shù)為0.919。

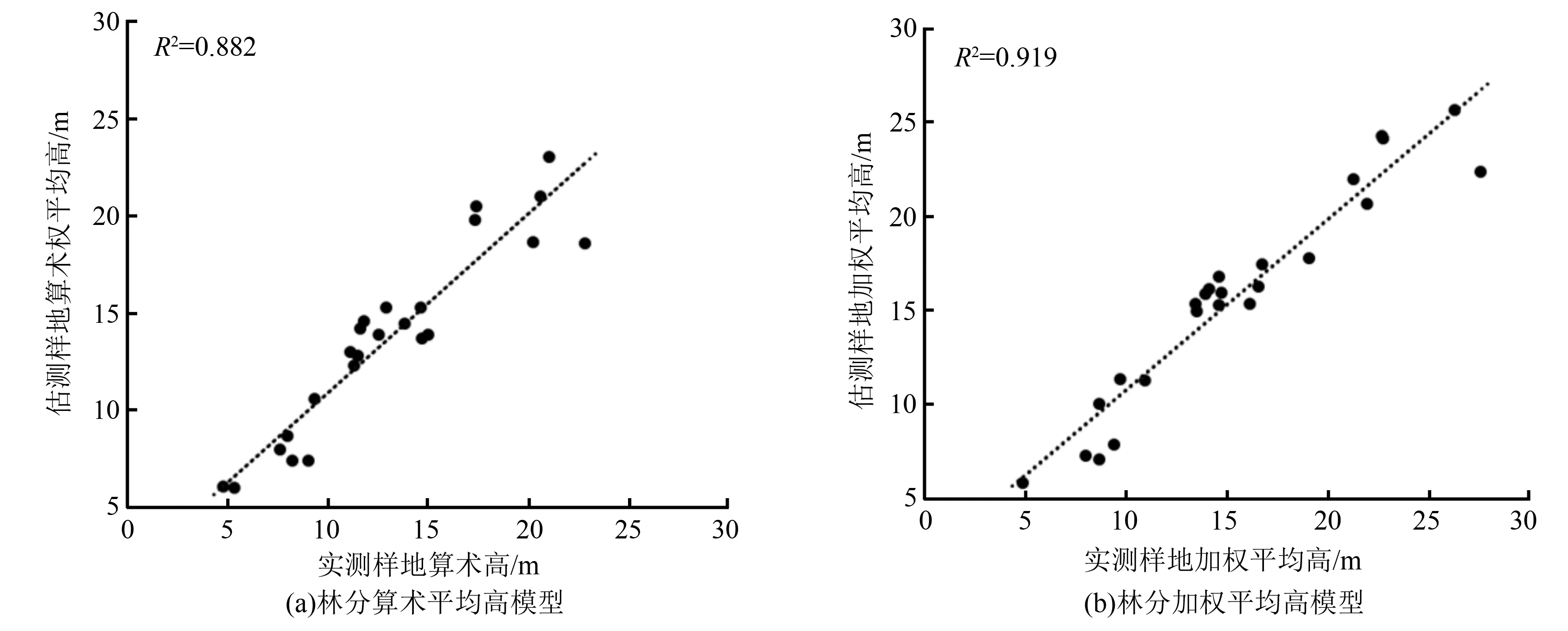
圖4 基于L-M算法估測(cè)的林分平均高與實(shí)測(cè)樹高對(duì)比圖

如圖5(a)、圖5(b)所示，分別為采用貝葉斯正則化訓(xùn)練算法構(gòu)建的林分算術(shù)平均高模型、林分加權(quán)平均高模型的預(yù)測(cè)值與實(shí)測(cè)值的相關(guān)關(guān)系，其決定系數(shù)分別為0.874、0.908。

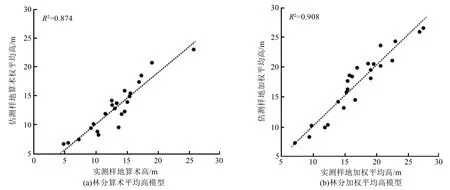
圖5 基于貝葉斯正則化算法估測(cè)的林分平均高與實(shí)測(cè)樹高對(duì)比圖

4.3 模型結(jié)果對(duì)比分析

為了更加直觀的體現(xiàn)實(shí)測(cè)林分平均高與各模型預(yù)測(cè)值之間的差異性，首先據(jù)公式(6)計(jì)算得各樣地的樹高估測(cè)精度P，且將各模型的決定系數(shù)、最高估測(cè)精度、最低估測(cè)精度、平均估測(cè)精度整理得表4；其次圖6描述了逐步回歸法、BP神經(jīng)網(wǎng)絡(luò)L-M算法、BP神經(jīng)網(wǎng)絡(luò)貝葉斯正則化算法分別構(gòu)建的林分算術(shù)平均高模型、林分加權(quán)平均高模型估測(cè)的林分平均高預(yù)測(cè)值和樣地實(shí)測(cè)值的差值。結(jié)合表4及圖6對(duì)模型結(jié)果進(jìn)行對(duì)比分析，具體如下。

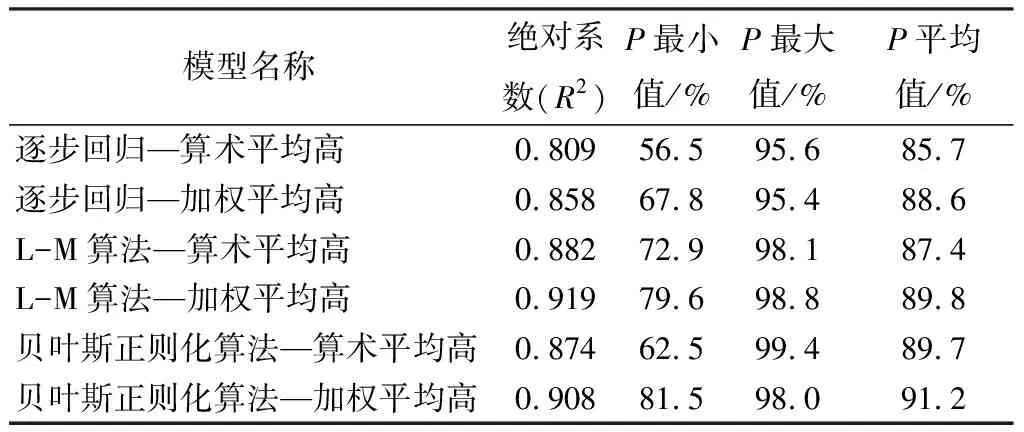
表4 不同算法構(gòu)建的林分平均高模型精度評(píng)價(jià)

(1)BP神經(jīng)網(wǎng)絡(luò)算法對(duì)數(shù)據(jù)的探究能力、模型的擬合效果優(yōu)于逐步回歸法。如圖5所示，樣地預(yù)測(cè)誤差最大為逐步回歸法構(gòu)建的算術(shù)平均高模型中的第15號(hào)樣地，其誤差達(dá)到6.78 m；從表4進(jìn)行分析可知，與逐步回歸法對(duì)比，L-M算法平均精度提升了6.7%、貝葉斯正則化算法平均提升了5.75%。

(2)林分加權(quán)平均高模型整體擬合精度優(yōu)于林分算術(shù)平均高模型。分別采用逐步回歸法、BP神經(jīng)網(wǎng)絡(luò)L-M算法、BP神經(jīng)網(wǎng)絡(luò)貝葉斯正則化法反演林分平均高模型時(shí)，加權(quán)平均高作為目標(biāo)值反演的模型R2比算術(shù)平均高作為目標(biāo)值時(shí)分別提升了4.9%、3.7%、3.4%。

(3)對(duì)BP神經(jīng)網(wǎng)絡(luò)來說，L-M算法、貝葉斯算法在實(shí)驗(yàn)中表現(xiàn)無明顯差異。L-M算法與貝葉斯正則化算法相比，其構(gòu)建的模型的平均R2僅高出0.95%。

(4)檢驗(yàn)樣本數(shù)據(jù)的樹高估測(cè)精度P最高為99.4%，最低為56.5%，總體平均估測(cè)精度均在85%以上，實(shí)測(cè)值與預(yù)測(cè)值無顯著偏離差異，在各模型的預(yù)測(cè)值與實(shí)測(cè)值的散點(diǎn)圖中驗(yàn)證了該結(jié)論。

圖6 各算法下估測(cè)不同林分平均高的樣地實(shí)測(cè)值和預(yù)測(cè)值的差值對(duì)比圖

5 結(jié)論與討論

本文結(jié)合研究區(qū)內(nèi)128塊圓形樣地的機(jī)載LiDAR點(diǎn)云數(shù)據(jù)、野外實(shí)測(cè)的樣地算術(shù)平均高數(shù)據(jù)、樣地?cái)嗝娣e加權(quán)平均高數(shù)據(jù)，提取了樣地區(qū)域內(nèi)的32個(gè)LiDAR點(diǎn)云特征變量，使用逐步回歸法、BP神經(jīng)網(wǎng)絡(luò)L-M算法、BP神經(jīng)網(wǎng)絡(luò)貝葉斯正則化算法對(duì)東北虎豹國(guó)家森林公園范圍內(nèi)的針葉純林的林分平均高進(jìn)行預(yù)測(cè)。

基于BP神經(jīng)網(wǎng)絡(luò)算法構(gòu)建的林分平均高估測(cè)模型的估測(cè)精度較高，優(yōu)于逐步回歸法構(gòu)建的林分平均樹高估測(cè)模型。采用24個(gè)檢驗(yàn)樣本對(duì)BP神經(jīng)網(wǎng)絡(luò)模型進(jìn)行評(píng)價(jià)，模型估測(cè)值與實(shí)際值的相關(guān)性較強(qiáng)，相關(guān)系數(shù)R2均在87%以上，高于逐步回歸法構(gòu)建的林分平均樹高估測(cè)模型。可以驗(yàn)證該算法對(duì)林分平均高估測(cè)的可行性。BP神經(jīng)網(wǎng)絡(luò)不同的訓(xùn)練算法對(duì)林分平均高的估測(cè)結(jié)果具有一致性。研究比較了貝葉斯正則化訓(xùn)練函數(shù)與L-M訓(xùn)練函數(shù)的性能，在不同目標(biāo)值情況下，兩種不同訓(xùn)練方法構(gòu)建的模型均能較好的預(yù)測(cè)林分平均高，雖然不同訓(xùn)練算法的評(píng)價(jià)精度略有差異，但整體相差較小。各樣地的斷面積加權(quán)平均高更適用于林分平均高估測(cè)模型的建立。對(duì)比逐步回歸法及BP神經(jīng)網(wǎng)絡(luò)算法構(gòu)建的估測(cè)模型發(fā)現(xiàn)，采用樣地加權(quán)平均高作為實(shí)測(cè)值時(shí)，模型的精度提升了3.4%～4.9%。

本研究所構(gòu)建的模型雖然能夠較好的估測(cè)林分平均高，但由于數(shù)據(jù)量的限制，未開展區(qū)分樹種的研究；且LiDAR數(shù)據(jù)與其他光學(xué)遙感數(shù)據(jù)源相結(jié)合獲取相應(yīng)的林分參數(shù)變量也有待進(jìn)一步實(shí)驗(yàn)。以機(jī)載LiDAR點(diǎn)云數(shù)據(jù)為依托，開展其他林分結(jié)構(gòu)參數(shù)的研究是筆者今后的努力方向。