超導故障限流器抑制短路電流直流分量的仿真分析

倪 輝， 黎 煒， 蘭潤棟， 項 彬， 丁 培， 喻 婷， 趙 慶， 羅金輝， 姚曉飛

(1. 國網寧夏電力有限公司電力科學研究院， 寧夏 銀川 750002； 2. 西安交通大學電力設備電氣絕緣國家重點實驗室， 陜西 西安 710049)

1 引言

隨著我國社會的發展和國民經濟的持續增長，電網規模越來越大。一方面，電力系統的裝機容量逐年擴大，且隨著特高壓工程的逐步發展、新型能源的不斷接入和電網聯系的進一步加強[1-4]，系統短路電流的水平也隨之增大，短路電流的直流分量也越來越大；另一方面，各種電力設備的X/R正逐漸增大，而為了限制短路電流水平采用的限流電抗器又進一步增加了系統的X/R值，使短路電流中直流分量時間常數不斷增加[5-7]。文獻[8,9]指出若觸頭分離時刻直流分量超過20%，則需考慮直流分量對開斷性能的影響，直流分量會導致短路電流總的有效值增大，電弧能量增大，加大了斷路器開斷短路電流的難度。文獻[10]將KEMA模型引入直流分量開斷仿真，結果表明，當斷路器的額定開斷能力包含20%的直流分量時，氣體燃弧的功率升高，臨界電弧參數如散熱功率常數比不考慮直流分量時大。綜上所述，逐漸增大的直流分量使斷路器的開斷負擔增大，嚴重時會導致開斷失敗，使整個系統崩潰。因此有必要研究抑制短路電流直流分量的方法，解決斷路器開斷能力不足的問題，保證系統的可靠運行。

目前，為解決短路電流超標，電網運行部門被迫采取主變停運、線路斷線、母線分列運行、加裝限流電抗器等方式限制短路電流[11-13]。上述運行方式的調整，或者降低了設備資產利用率，或者降低了電網供電可靠性，而加裝限流電抗器又會使短路電流直流分量衰減時間常數增大，都會對電網的運行造成威脅。超導型故障電流限流器集檢測、限流于一身，系統正常運行時不會產生損耗，系統發生故障時迅速反應，可抑制線路短路電流、降低對高壓斷路器開斷容量的要求，且能自動恢復[14-17]，是保護電力系統最理想的限流裝置之一。

然而，超導故障限流器對于短路電流直流分量和不同直流時間常數下故障情況的影響規律尚不清楚。本文的研究目標為獲得超導故障限流器對于短路電流直流分量的抑制效果和不同直流時間常數下故障的影響規律，為系統選取合適阻值的超導限流器，為斷路器分閘時間提供理論依據。本文通過在Matlab/Simulink中搭建超導限流器模型和系統電路模型，對比仿真了有無電阻型超導限流器、同一直流時間常數下不同阻值的超導限流器、同一阻值超導限流器下不同直流時間常數時系統發生故障的情況，對不同情況下的短路電流直流分量進行了分析，討論了超導限流器失超電阻的選取方法。

2 仿真設置

2.1 仿真電路模型建立

在Matlab/Simulink模塊中搭建圖1所示的模型。圖1(a)模擬電路發生短路的情況，交流系統為330 kV，線路電阻Rline=0.52 Ω，線路電抗Lline=0.023 5 H，負載電阻Rload=7.24 Ω，負載電抗Lload=0.326 5 H，此時線路的直流時間常數為45 ms，額定電流為3.0 kA，短路電流峰值為110 kA，穩定值為63 kA。圖1(b)為模擬系統安裝超導限流器后發生短路的情況。圖1(c)模擬只存在線路阻抗并且超導限流器變化和圖1(b)中短路時一樣，目的為提取圖1(b)系統發生短路時隨著超導限流器電阻變化而變化的交流分量。

圖1 仿真電路圖Fig.1 Simulation circuit diagrams

2.2 超導限流器模型建立

常用的超導限流器模型有：時域模型、基于E-J特性曲線的物理模型、從實際短路故障中的電壓、電流波形計算得到的電阻模型。

時域模型將失超電阻看作一個時變函數。一種典型的超導帶材時域模型的函數如式(1)所示，表示短路故障發生后，超導帶材從超導態過渡到失超態的時間內，電阻從0上升到RSC。

(1)

式中,RSC為失超電阻；TSC為時間常數。在該模型中RSC、TSC需要通過實驗數據擬合[18,19]。

高溫超導帶材滿足超導E-J特性曲線，在失超瞬間，超導失超電阻具有很強的非線性，上升速度快。基于E-J特性曲線建立的超導帶材模型的實現方法為當實際電流I通過超導帶材時，由E-J特性曲線計算出兩端電壓，再根據歐姆定律，求出此時的電阻R。一種典型超導帶材物理模型的電阻變化函數如式(2)所示，電流密度J和溫度T決定超導帶材的電阻值RSFCL，一共分為三個階段。

(2)

式中，Jc為臨界電流密度；Tc為臨界溫度；n為超導體特征參數。

超導帶材E-J對數曲線如圖2所示，超導電阻的轉換過程可以分為四個階段：超導態、磁通蠕動階段、磁通流動階段和正常態。

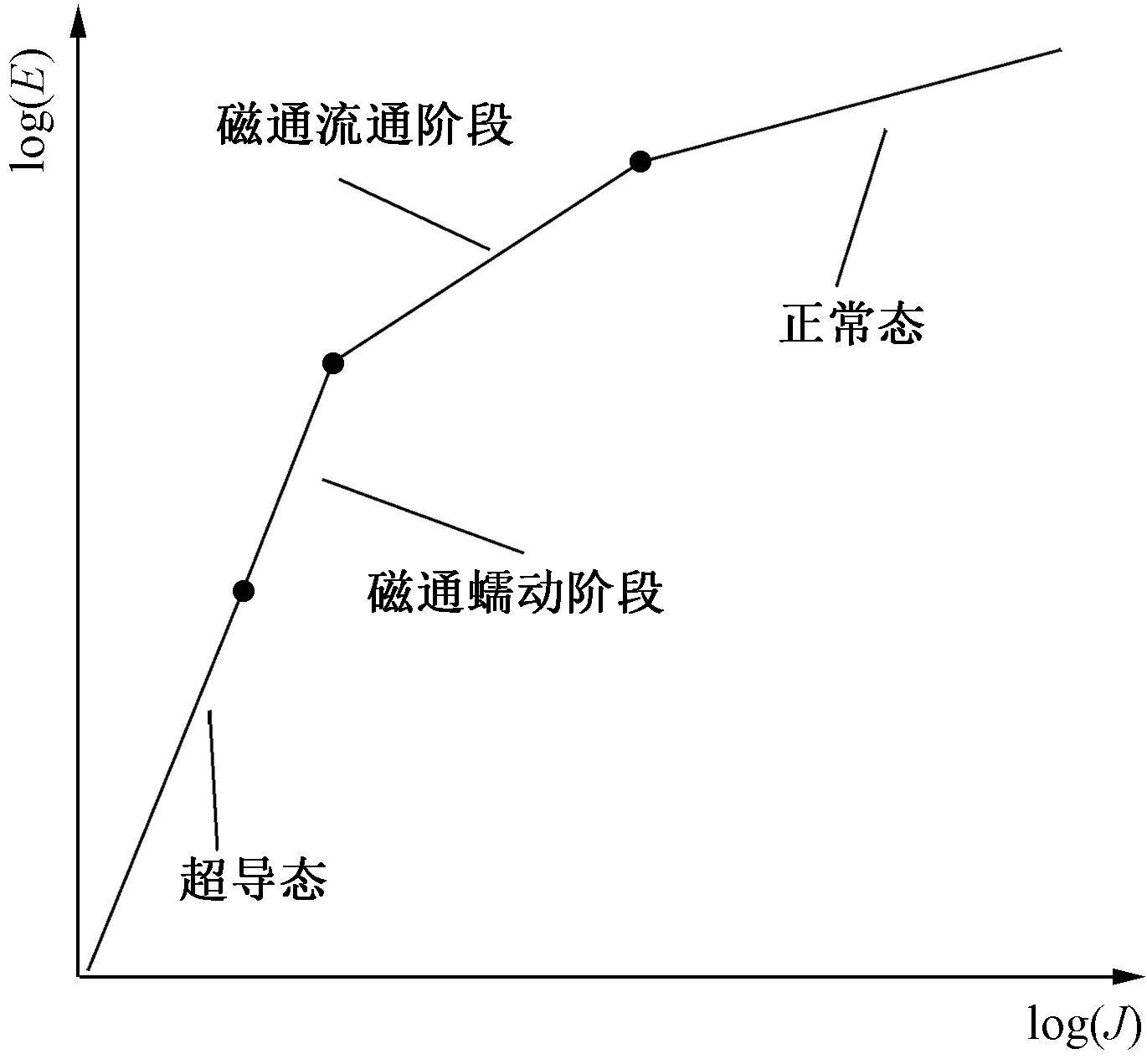
圖2 超導帶材E-J對數曲線Fig.2 E-J log curve of superconducting tape

仿真時考慮斷路器額定開斷容量的情況，因為在額定容量，當系統還有較大直流分量時，斷路器存在開斷失敗的風險。目前高壓斷路器的開斷能力多為63 kA。仿真系統額定電壓330 kV，短路電流峰值110 kA，有效值63 kA。由于該短路電流遠大于超導帶材的臨界電流，超導帶材迅速失超并且在直流分量衰減完畢之后的短路電流仍遠大于超導帶材的臨界電流，因此通過E-J特性曲線計算出的失超電阻與時域模型表示的失超電阻基本一致。本文根據實驗測得數據構造不同穩定失超阻值的失超曲線，使用時域電阻模型，避免了用復雜運算建立E-J特性曲線模型。

實驗選美國超導公司(AMSC)的8602高溫超導帶材，帶材具體參數如表1所示，測量超導帶材失超電阻的實驗電路如圖3所示，圖3中L=0.1 mH，C=100 mF，用高壓探頭測量超導帶材兩端電壓，霍爾傳感器測量流過帶材的電流，根據帶材電壓與電流的比值獲取失超電阻實驗波形，測量結果如圖4所示，用分段線性函數擬合實驗失超電阻波形得到失超電阻擬合曲線。

表1 超導帶材參數Tab.1 Superconducting tape parameters

圖3 失超電阻測試電路圖Fig.3 Quench resistance test circuit diagram

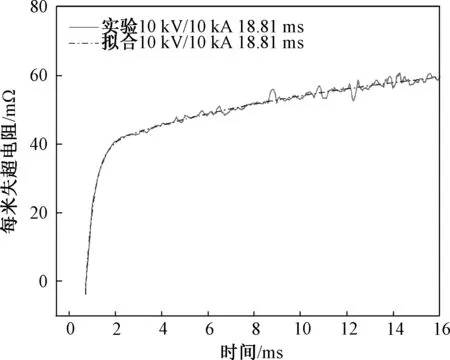
圖4 8602帶材失超特性曲線Fig.4 8602 tape measurement results

3 仿真結果

3.1 短路電流直流分量

仿真結果如圖5所示，圖5為發生短路故障時的短路電流全波形和交直流分量，對于直流時間常數為45 ms的330 kV交流系統，20 ms時發生短路，其短路電流峰值接近110 kA，起始直流分量為58 kA左右，衰減時間很長，在86.4 ms時衰減至12.6 kA(短路電流有效值的20%)。

圖5 短路電流波形圖Fig.5 Short-circuit current waveforms

3.2 不同超導阻值下的直流分量

選取電力系統標準時間常數45 ms，分別仿真了超導限流器穩定阻值為0 Ω、2.5 Ω、5 Ω、7.5 Ω、10 Ω、15 Ω、20 Ω、30 Ω時的短路電流和直流分量，獲得不同阻值的超導限流器對短路電流和短路電流直流分量的抑制效果。

圖6為不同阻值的超導限流器失超電阻R-T特性圖，用時域電阻模型模擬，其中RSC、TSC根據實驗測量數據擬合。以圖4為例，0～1 ms時間內，電阻主要由超導帶材的YBCO超導層決定，失超電阻變化率達到40 mΩ/(m·ms)。由高溫超導的E-J特性可得，電流密度增加使超導內部電場強度呈冪指數增加，失超電阻迅速增大，增加的電阻值將會使超導帶材產生更多熱量，溫度上升導致臨界電流密度進一步減小，電場強度進一步擴大，從而形成正反饋。2 ms之后，超導進入完全失超狀態，電阻主要取決于超導帶材的不銹鋼穩定層，形成第一個拐點。14 ms后，溫度和電流密度對不銹鋼的電阻率影響較小，電阻值增加緩慢。同時，在該時間段內，超導帶材溫度高于臨界溫度，超導產熱和放趨于平衡，失超電阻上升率降低最后趨于平穩，形成第二個拐點，因此時域模型大多具有兩個拐點。

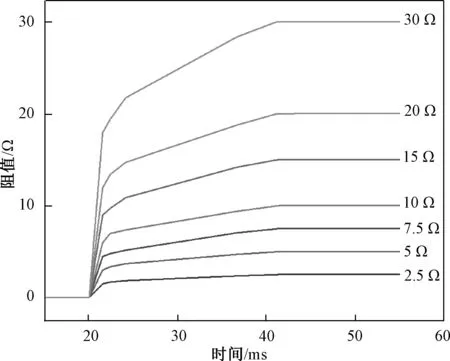
圖6 失超電阻R-T特性圖Fig.6 R-T characteristic diagram of quench resistance

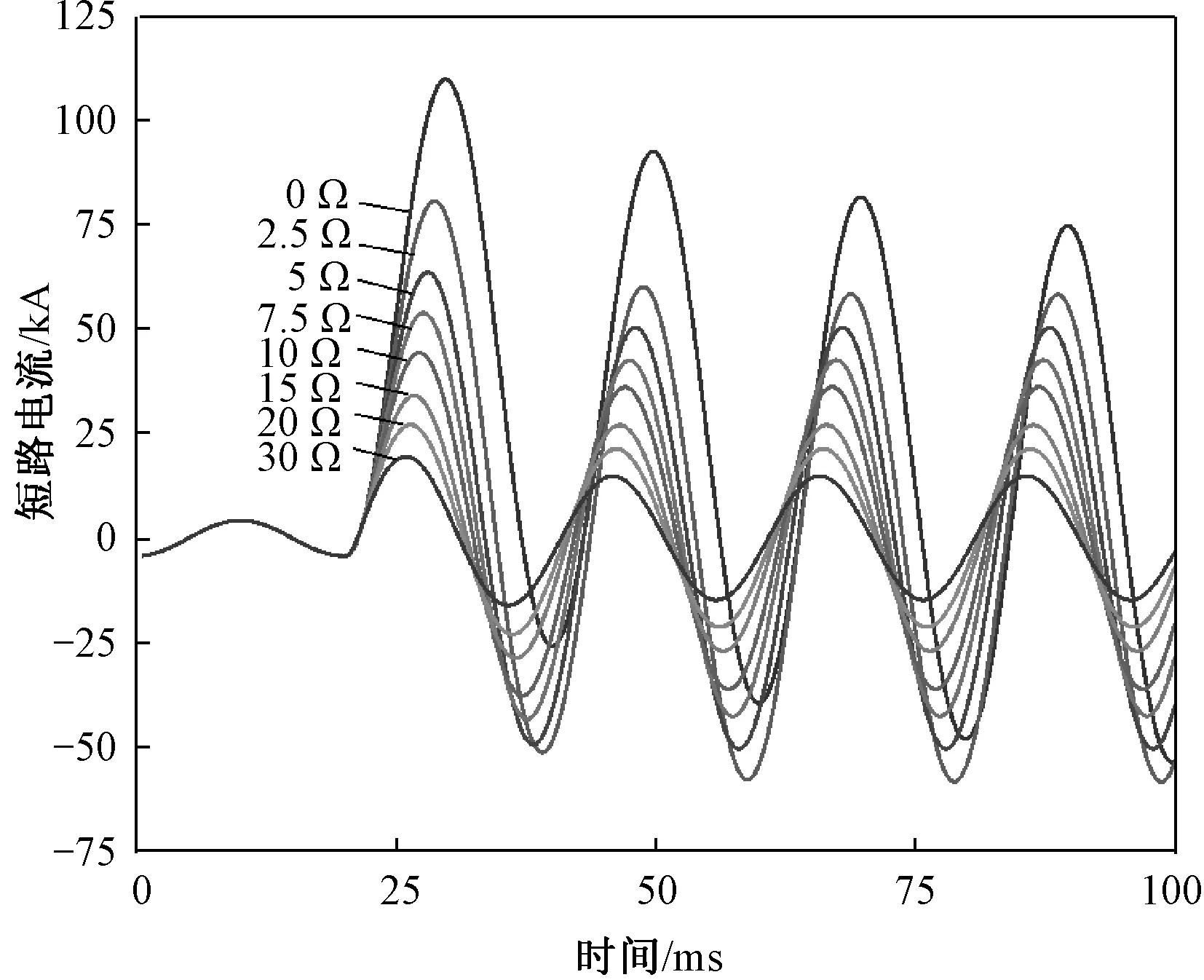
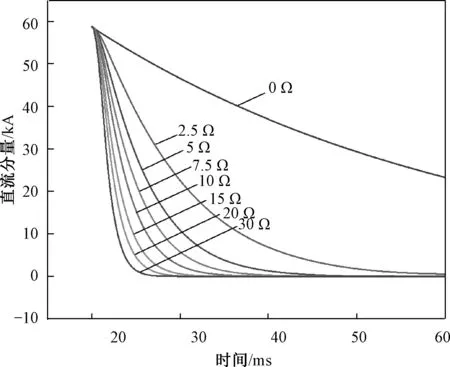
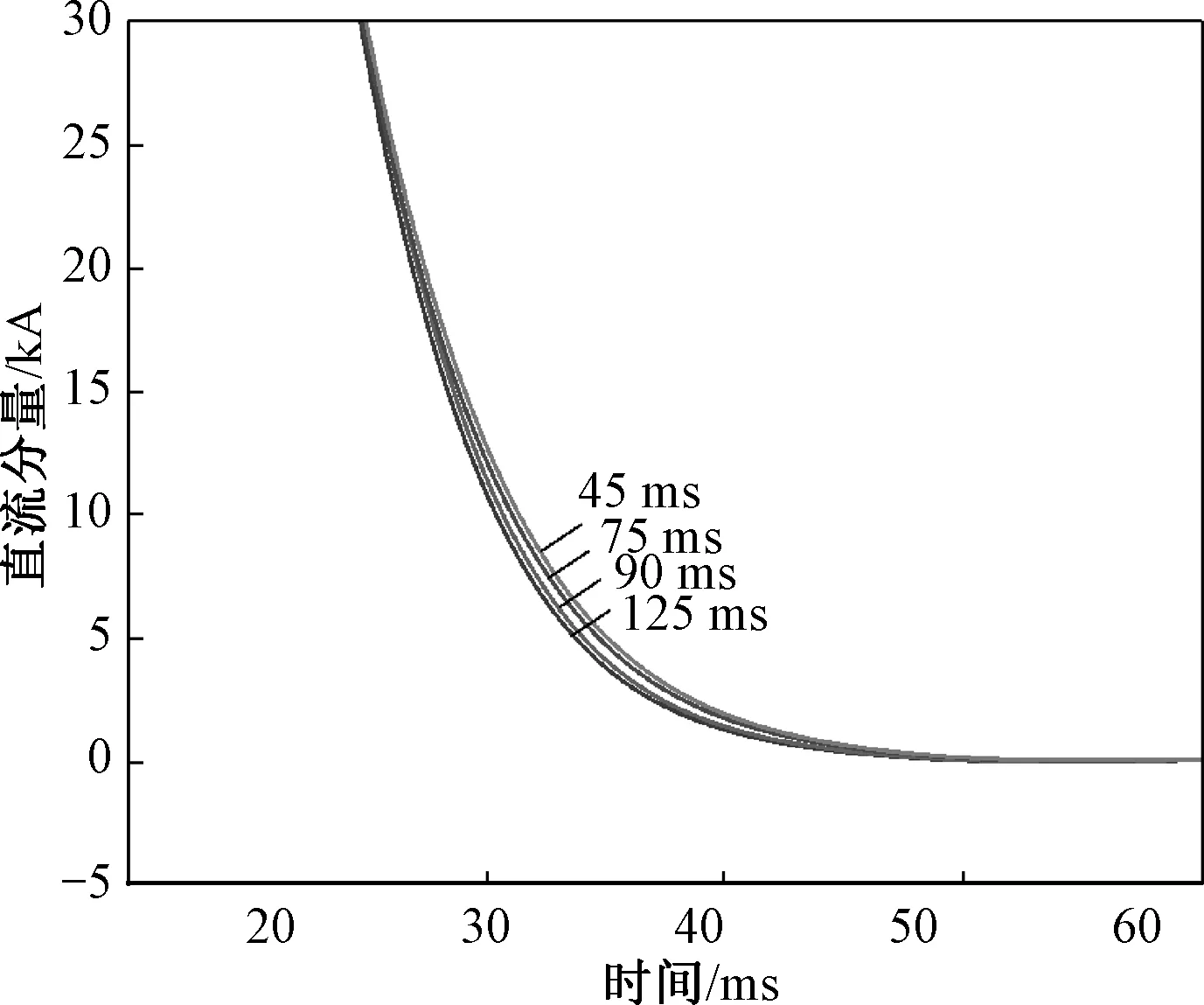
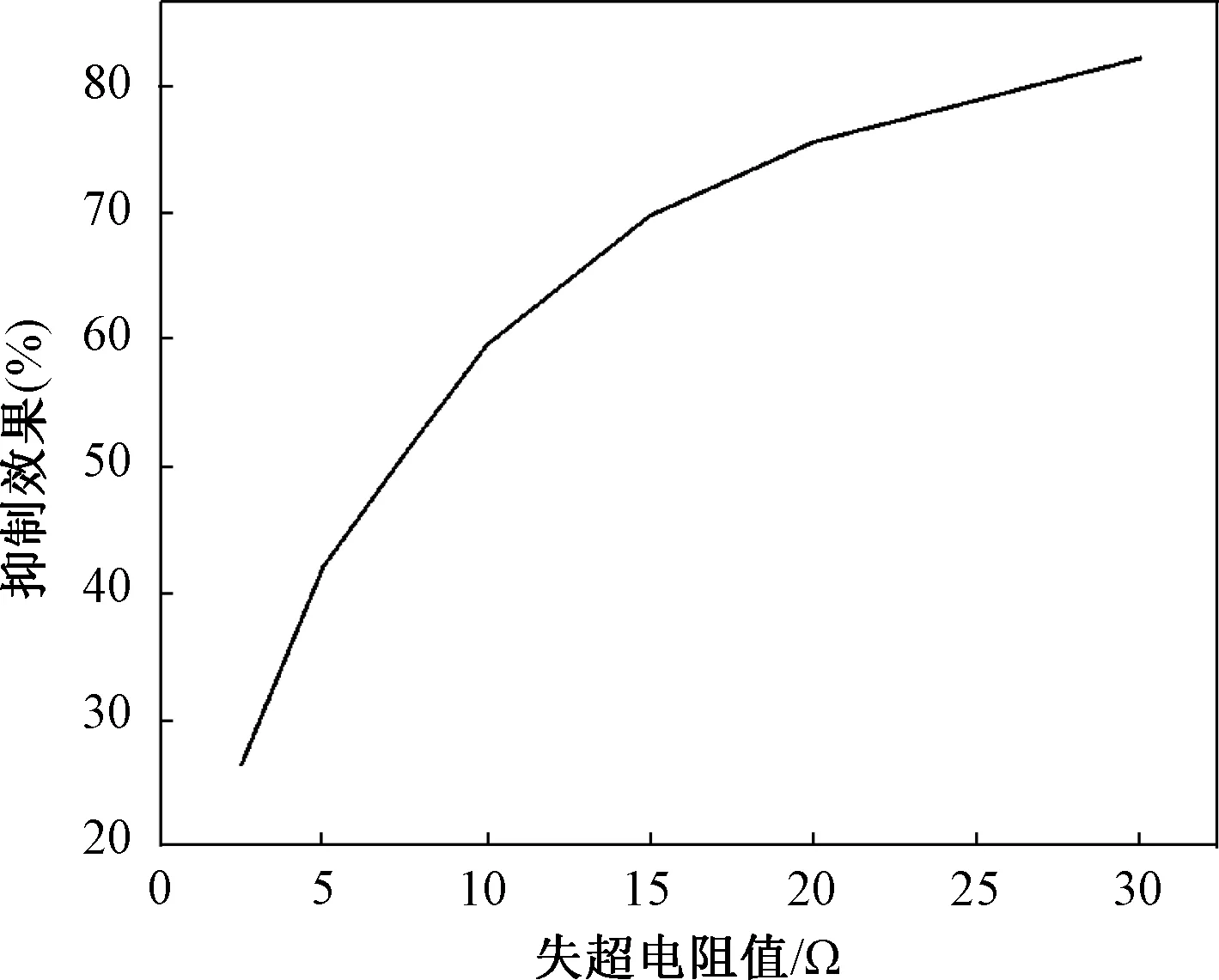
基于不同充電電流下超導失超電阻變化曲線建立的時域模型分段函數表達式為：R=at(0

表2 失超電阻表達式參數Tab.2 Parameters of quench resistance expressions

仿真結果如圖7、圖8所示。圖7為失超電阻穩定值為0 Ω、2.5 Ω、5 Ω、7.5 Ω、10 Ω、15 Ω、20 Ω、30 Ω時的短路電流波形圖。由于超導帶材在短路故障發生時能自動反應，無需控制電路，響應時間極短，因此超導限流器能實現首半波限流，限流后短路電流峰值分別為110 kA、80.8 kA、63.7 kA、53.9 kA、44.4 kA、34.2 kA、27.2kA、19.6 kA，對短路電流峰值的抑制效果分別為0%、26.5%、42.1%、51%、59.6%、68.9%、75.3%、82.2%。

圖7 不同失超電阻下短路電流波形圖Fig.7 Short-circuit current waveforms of different quench resistances

圖8是為失超電阻穩定值為0 Ω、2.5 Ω、5 Ω、7.5 Ω、10 Ω、15 Ω、20 Ω、30 Ω情況下的直流分量衰減趨勢，加超導限流器后，直流分量均在60 ms內衰減完畢。穩定值為2.5 Ω的失超電阻，在34.9 ms將直流分量抑制到12.6 kA (短路電流有效值的20%)，穩定值≥5 Ω的失超電阻，在短路發生后10 ms之內將直流分量抑制到12.6 kA。

圖8 不同失超電阻下直流分量衰減趨勢Fig.8 DC component decaying trendency of different quench resistances

3.3 不同直流時間常數下的直流分量

根據3.2節的仿真結果，當超導限流器失超電阻為5 Ω時，就能在10 ms內將直流分量限制到斷路器額定開斷容量的20%，使斷路器能可靠開斷限制后的電流。因此，仿真設置超導限流器穩態阻值為5 Ω。《高壓交流斷路器》[20]中規定標準時間常數為 45 ms，特殊時間常數為 60 ms、75 ms、120 ms，因此仿真研究5 Ω的超導限流器阻值對4種直流時間常數的限制效果。4種時間常數下的電路阻抗參數見表3。

表3 不同直流時間常數下的電路參數Tab.3 Circuit parameters with different DC time constants

圖9為4種時間常數下的直流分量衰減趨勢。直流分量是由短路過程中感應電勢和短路回路阻抗所確定的按指數規律衰減的電流，它的衰減速度由直流時間常數τ(τ=L/R)決定，τ越大，衰減越慢。仿真結果顯示，在不同直流分量下，5 Ω的超導失超電阻值均在短路發生后10 ms之內就將直流分量限制到12.6 kA，斷路器額定開斷容量的20%。而且不同時間常數下，直流分量變化曲線差距較小，超導限流器具有很高的普適性，在不同時間常數下抑制效果相近。上述結論證明超導限流器的設計阻值能很好地滿足不同時間常數的系統，具有良好適應性，同時也降低了超導限流器的設計難度。

圖9 不同直流時間常數下直流分量衰減趨勢Fig.9 DC component decaying trendency of different DC time constants

4 討論

4.1 超導限流器失超阻值的優化設計方法

3.2節的結果表明，標準時間常數45 ms情況下，超導限流器對短路電流峰值和直流分量的抑制效果與阻值成正比。失超阻值對短路電流峰值抑制效果如圖10所示。仿真結果顯示，失超阻值和短路電流峰值抑制效果百分數的關系曲線斜率逐漸降低，因此低的失超電阻具有更高的性價比。超導失超電阻應同時滿足對短路電流幅值和直流分量的抑制要求。超導限流器失超后呈現大電阻，能顯著降低系統短路電流幅值，但增大失超電阻會使成本呈指數增加，因此，系統短路時，通常限流器對短路電流的限流深度達到30%～50% 即可滿足需求，在該330 kV高壓系統，超導阻值為3.5～7.5 Ω即滿足要求。超導失超后的大電阻不僅顯著降低了短路電流幅值，也使系統的直流分量衰減時間常數顯著降低。阻值≥5 Ω的超導限流器，在短路發生后10 ms之內將直流分量抑制到12.6 kA(短路電流有效值的20%)，即滿足了直流分量的抑制要求。綜上所述，該系統超導限流器失超阻值優化設計為5 Ω。

圖10 失超電阻對短路電流峰值抑制效果Fig.10 Quench resistance on short-circuit current peak suppression effect

4.2 超導限流器限流效果

對于直流時間常數τ=L/R，不加超導限流器發生短路時，直流分量衰減時間不同，需根據情況設置斷路器的分閘時間。3.3節的結果表明，當超導限流器失超電阻為5 Ω時，標準時間常數45 ms和特殊時間常數 60 ms、75 ms、120 ms情況下，線路短路電阻僅占超導限流器失超阻值的5%～10%，因此，時間常數為45～120 ms時，使系統安裝超導限流器后的時間常數τ相差小于10%，在不同時間常數下，超導限流器的限流效果相差小于10%。因此，超導限流器適用于不同工況下的短路故障，且無需更改斷路器的分閘時間，降低了系統超導限流器和保護設備的設計難度和分散性，拓寬了利用超導限流器抑制系統直流分量的適用范圍。

5 結論

現有超導直流限流器設計方法主要考慮限流深度和限流速度，往往需要具有60% 甚至以上的限流深度以及限制短路電流快速增長的能力。而在交流系統中，由于有自然過零點的存在，對限流深度的要求有所降低，往往達到30%～50% 即可，本文在此基礎上更加注重對直流分量和直流分量時間常數的考慮，以一定時間內對直流分量的限流效果和對直流時間常數的改善作為評判標準來選擇合適阻值的超導限流器。提出使用超導限流器在限制短路電流幅值的同時，抑制短路電流直流分量的方法，仿真結果表明超導限流器對直流分量的抑制效果非常明顯，且適用于不同工況下的短路故障，同時為超導故障限流器失超阻值的選取提供了理論依據。

具體結論如下：

(1)標準時間常數45 ms下，超導限流器對短路電流峰值和直流分量的抑制效果與阻值成正比，可從對短路電流和直流分量的抑制效果兩方面為超導限流器阻值的選取提供判據。

(2)文中330 kV高壓系統選取阻值為5 Ω的超導限流器，限流深度達到40%，短路發生后10 ms之內將直流分量抑制到短路電流有效值的20%。

(3)標準時間常數 45 ms和特殊時間常數60 ms、75 ms、120 ms 4種工況下，超導限流器均可適用，且無需更改斷路器分閘時間，降低了保護系統設計難度，設計的超導限流器具有良好的普適性。