基于連接信息的無線傳感器網絡邊界識別方法

葛玉君

（江南大學，江蘇 無錫 214122）

0 引言

無線傳感器網絡（Wireless Sensor Network，WSN）[1-2]在生活中應用廣泛。邊界檢測主要基于位置[3]、基于統計[4]、基于連接[5]。基于位置與統計的方法，要么需要傳感器精確的坐標信息，代價昂貴；要么要求高節點密度，精度與網絡普適性差。基于連接性的方法，實現成本低于位置方法，精度優于統計方法，適用性強。本文提出的算法基于兩跳鄰居節點的連接信息。引入的中心性方法，常用來判斷節點的重要性，識別WSN邊界是其副產品[6]。通過計算中介中心性，量化節點重要程度。仿真表明，在邊界識別問題上有良好的適用性。

1 中介中心性

1.1 概念

最著名的中間度量為Freeman[7]首次在圖論中引入的中介中心性，將中心性與信息控制相聯系，描述一個節點被其他節點的需要程度[8]。

其中，σst為節點s到節點t的最短路徑數量，σst(v)為從節點s到t的所有最短路徑中經過節點v的最短路徑的數目。由定義求解中心性過于復雜，故通過引入節點對依賴值對定義實現簡化[9]。據此Brands提出目前已知的最快的算法。

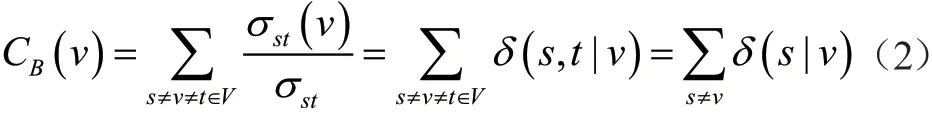
1.2 中心性與邊界的關系

由定義知，節點的中介中心性越大，越可能靠近網絡中心[10]，反之，中心性值越小，成為邊界節點的概率就越大。WSN中，高中心性節點（圖1中節點1）可促進節點間直接或間接通信，對從任何節點開始的信息流都至關重要。基于這一發現，可以通過計算節點的中心性值從而確定邊界節點。

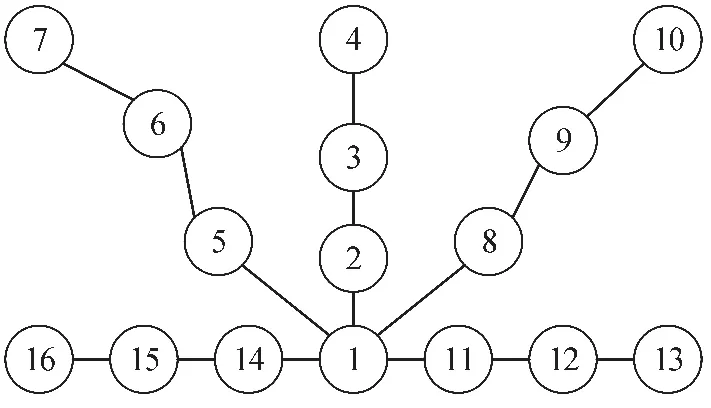
圖1 簡單網絡

2 算法介紹

2.1 模型假設

WSN由G(V,E)表示，其中V為節點集，E是連接節點邊的集合。節點i的k跳領域圖，使用Gi(Vi,Ei)表示。節點均具各向同性且ID信息唯一。考慮實際應用中環境的友好程度，傳感器均勻分布在感知區域，可具任意形狀的通信范圍。

2.2 算法實現

精確計算大型網絡中節點的中心性，其網絡和計算成本及其昂貴。在實際WSN中算法復雜度隨節點數增加而增加，如鄰接矩陣的規模即達到O(N2)。因此將全局問題轉化為局部求解。如表1所示，k從2開始取。算法主要思想是，基于邊界節點的中心性值較低。對節點對之間的路徑計算，主要通過最短路徑算法（不考慮多次經過同一個節點的情況）。故對邊界識別問題，采用近似化算法，進行分布式檢測。先為每個傳感器構建其k跳鄰域圖，根據鄰域圖計算節點的中介中心性。再比較中心性的值選擇值較低的節點為邊界節點。

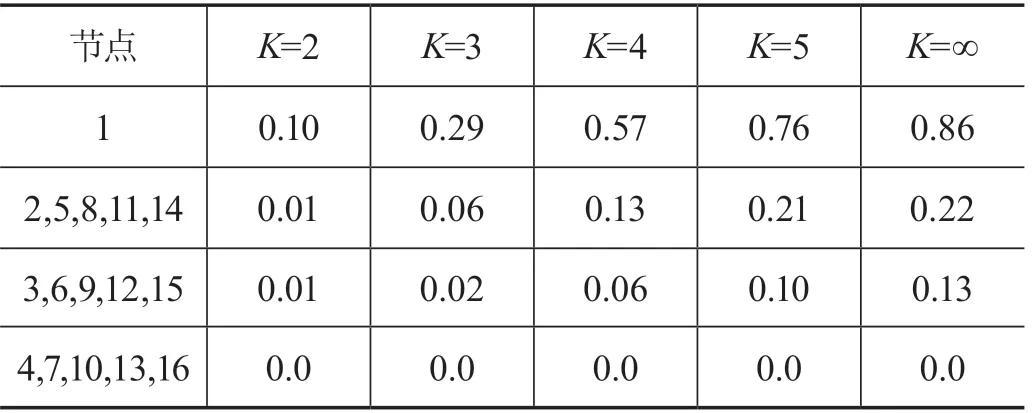
表1 不同k值的節點中心性

3 仿真與分析

為便于仿真，假設節點的通信區域為以節點為中心的圓，通信半徑rc，在圖上僅標注通過算法識別的邊界節點。

3.1 不同k值

圖2為k取不同值時所得結果，WSN總節點數為3 236，平均節點密度為12。實驗表明僅使用原始計算的小部分，結果就具很高的有效性。另一方面，由于算法的復雜度主要在于k跳領域圖內的節點數，故當k取值越小，其算法復雜度也越小。表2為k取不同值時的誤認率情況。在節點密度恒定的網絡中，通過算法運行時間和邊界誤認率的綜合比較，證明2-中介中心性測度是較好的中心性近似選擇，且對于邊界識別算法具有較好的使用性。

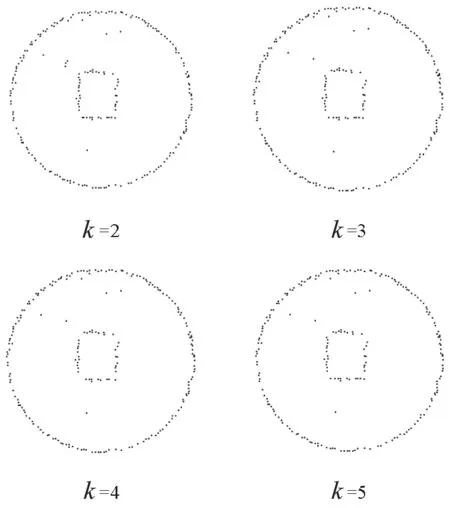
圖2 不同k值結果

表2 不同k值誤認率

故對于每個節點，只使用k個步驟來計算最短路徑，通過BFS算法遍歷每個節點的k跳鄰居節點，節省大量計算時間，且對結果度量的影響最小。

3.2 不同形狀的邊界

WSN平均節點密度為10，k取2，在不同形狀邊界的網絡中，結果如圖3所示。左圖為網絡部署，右圖為檢測出的邊界。結果表明，本算法適用性較強，對不同形狀的邊界均適用良好。

圖3 不同邊界形狀的WSN

4 結語

本文提出一種邊界識別算法，通過引入中心性概念識別出邊界點。綜合考慮算法的復雜度與結果的誤認率，選擇通過節點的2-中介中心性，從而找到WSN邊界節點。