基于NNCA的某破障武器模糊自適應動態面控制

沙燁鎮，余世航，陳機林

(1 南京理工大學機械工程學院,南京 210094；2 湖北江山重工有限責任公司,武漢 430000)

0 引言

某型火箭破障器的電液伺服系統由于液壓系統自身存在流量-壓力特性、液壓閥死區、油液收縮、飽和等非線性因素，使得傳統控制策略的控制精度難以達到預期的要求。

為了精確控制電液伺服系統，國內外學者針對系統的非線性問題，提出眾多控制方法。文獻[1]基于反步設計法，設計了一種自適應控制器，使得控制信號在任意誤差內能跟蹤期望信號。文獻[2]基于動態面濾波法設計的自適應魯棒位置控制器，確保了系統的響應精度和速度。文獻[3]針對一類不確定非時變系統，僅采用一個模糊系統就讓所有的未知函數得到了補償，大大簡化了控制器的結構。由于電機控制和電液伺服控制在動態方程的非線性參數形式上有相似性，文中對電液伺服系統的控制策略在后推法的基礎上加入低通濾波器，采用了動態面控制方法，解決了back_stepping方法中微分項爆炸的問題。針對動態方程中的未知非線性函數,通過模糊邏輯系統來進行逼近。

采用動態面控制方法來設計控制器，對動態方程中的未知函數通過基于最近鄰聚類算法的模糊邏輯系統來逼近[4]。最后通過Simulink來驗證控制器的有效性。

1 破障武器電液伺服系統建模

1.1 破障武器電液伺服系統原理

電液伺服系統原理圖如圖1所示。

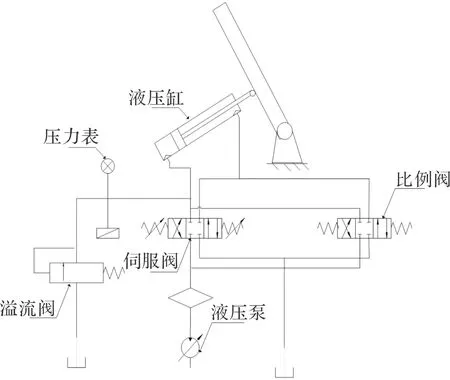
圖1 破障武器液壓伺服系統原理圖

1.2 電液伺服系統數學模型

電液伺服閥流量方程為：

qL=Kqxv-KcpL

(1)

式中:qL為液壓流量;pL為負載壓力;Kq為閥的流量增益;Kc為閥的流量-壓力系數;xv為閥芯位移量。

根據液壓缸的流量連續方程可以求得：

(2)

式中:xp為活塞位移;Ctp為液壓缸總泄露系數;Vt為總壓縮容積;βe為有效體積彈性模量。

壓力和負載的力平衡方程為：

(3)

式中:K為負載彈簧剛度;FL為作用在活塞上的外力。將式(1)～式(3)整理并做拉普拉斯變換可得：

(4)

xp=

(5)

1.3 電液伺服系統的狀態空間模型

電液伺服系統的簡化方框圖如圖2所示,將伺服放大器等效為比例環節，電液伺服閥等效為二階震蕩環節。放大器的增益為Kv,伺服閥的增益為Ksv,電壓信號為u，所以：

圖2 電液伺服系統簡化方框圖

xv=KvKsvu

(6)

將式(6)代入式(5)中，可以得到電壓信號u和xp的關系：

(7)

(8)

(9)

式中:u為系統輸入;yout為系統輸出;Kce為總流量壓力系數，Kce=Kc+Ctp。

2 模糊自適應動態面控制器設計

2.1 控制器設計

從式(8)不難看出，這是一個典型的下三角結構，針對該類型的電液伺服控制問題，可采用反步控制方法[5]，但存在微分項爆炸的問題。因此，將虛擬控制通過一個一階濾波器，從而產生一個新的變量，這就是動態面控制思想。

控制器的設計步驟為：

第一步： 液壓缸按照設想的位移x1d運動，定義運動誤差S1：

S1=x1-x1d

(10)

其導數：

(11)

選擇虛擬控制量：

(12)

將α2通過一階濾波器，產生變量x2d：

(13)

第二步：定義動態面：

S2=x2-x2d

(14)

其導數：

(15)

選擇虛擬控制量：

(16)

將α3通過一階濾波器，產生變量x3d：

(17)

第三步：定義動態面：

S3=x3-x3d

(18)

其導數：

(19)

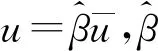
(20)

其中γβ,ηβ是已知參數。

另外由于f(x1,x2,x3)內有未知參數θ，用模糊邏輯系統F(x)[6]來逼近f(x1,x2,x3)。令：

(21)

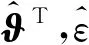
所以控制器設置為：

(22)

其中:k1,k2,k3為控制器的可調參數;τ2,τ3為濾波器的時間常數。取自適應律為：

(23)

圖3是模糊自適應動態面控制器的結構框圖。

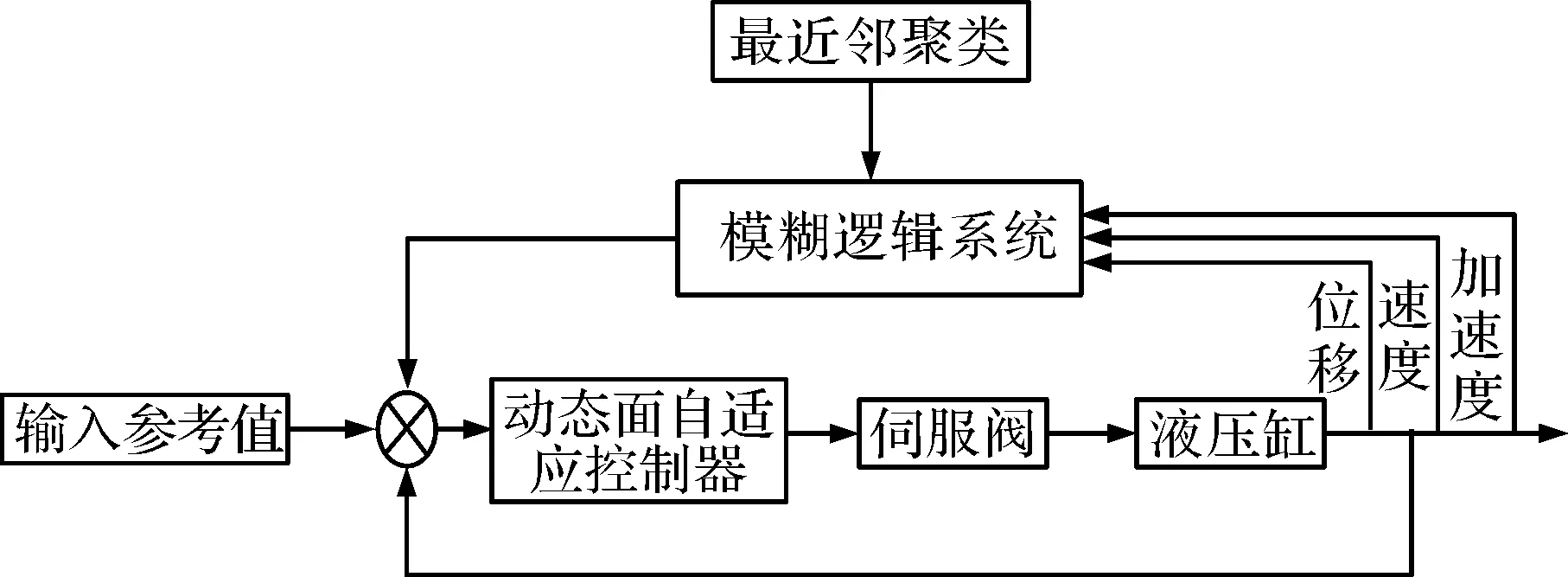
圖3 模糊自適應動態面控制器的結構框圖

2.2 穩定性證明

定義：

zi=xd-αi=-τixid,i=2,3

(24)

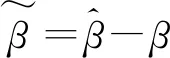
(25)

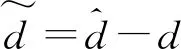
(26)

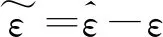
(27)

動態面微分方程為：

(28)

(29)

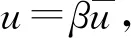
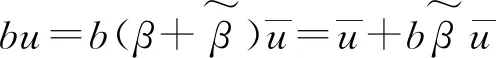
(30)

根據式(17)，式(22)，式(30)可得：

(31)

分析z2,z3的微分方程，由式(12)，式(13)可得：

(32)

對式(32)兩邊求導可得：

(33)

同理:

(34)

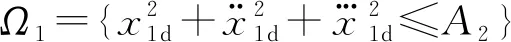
定義電液伺服系統的李亞普諾夫函數：

(35)

其中:

(36)

(37)

(38)

(39)

同理:

(40)

又有：

(41)

(42)

(43)

所以：

(44)

(45)

根據Young’s不等式：

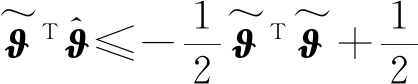
(46)

可得：

(47)

將式(45)代入式(43)得：

(48)

令：

(49)

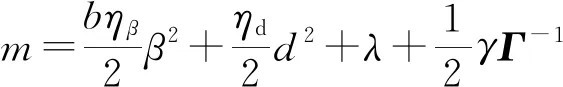
(50)

所以：

(51)

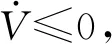
解式(51)可得：

(52)

而且：

(53)

由以上證明可知，存在k1,k2,k3和濾波器時間常數τ2,τ3，使得設計的模糊動態面自適應控制器保證閉環系統半全局穩定,輸出yout半全局漸進跟蹤期望軌跡x1d。

3 基于最近鄰聚類算法設計模糊邏輯系統

由式(8)可知，θ1,θ2,θ3是電液伺服系統的未知參數，在作為模糊系統的輸入時，實際上可以用x1,x2,x3來代替(即液壓缸的位移、速度、加速度)。定義模糊集，用負大(NB)、負小(NS)、零(ZR)、正小(PS)、正大(PB)來表示，于是有x1={NB，NS，ZR，PS，PB}，x2={NB，NS，ZR，PS，PB}，x3={NB，NS，ZR，PS，PB}，y={NB，NS，ZR，PS，PB}；液壓缸的實際輸出范圍為[-500,+500]，單位為mm；速度范圍為[-0.5,+0.5],單位為m/s；加速度范圍為[-1,+1]，單位為m2/s。選用合適的量化因子，使其對應的模糊論域為：x1={-2,-1,0,1,,2},x2={-2,-1,0,1,2},x3={-2,-1,0,1,2},由于模糊控制的輸出在反模糊化前無法獲得[7]，因此可假設輸出的模糊論域為y={-2,-1,0,1,2}。

1)選擇高斯函數作為隸屬度函數

(54)

2)選擇模糊規則

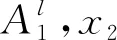
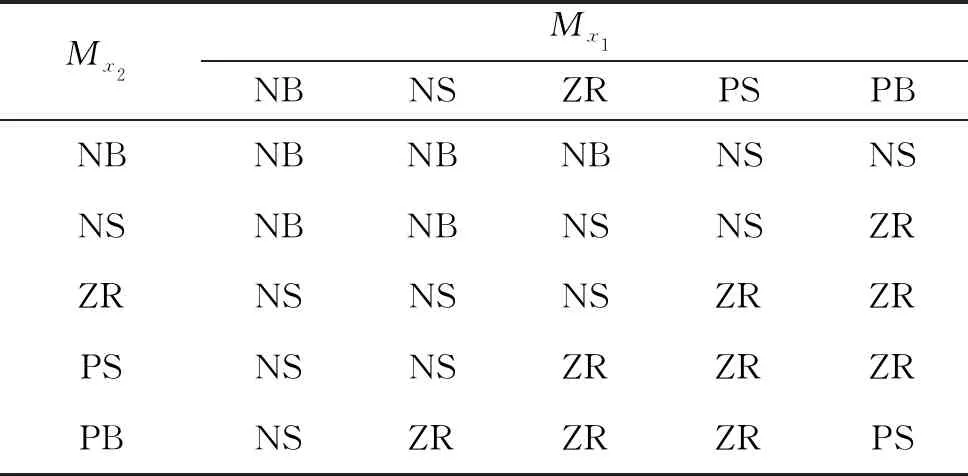
表1 x3模糊變量為NB時y的模糊規則表

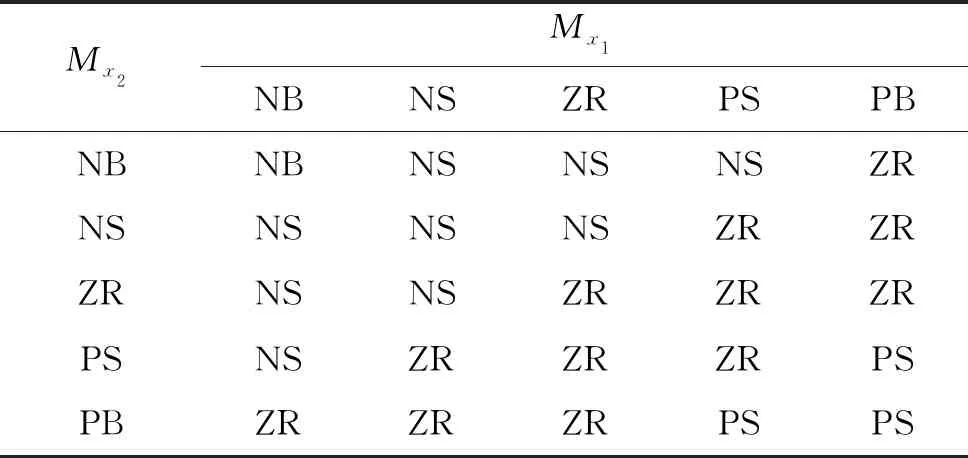
表2 x3模糊變量為NS時y的模糊規則表

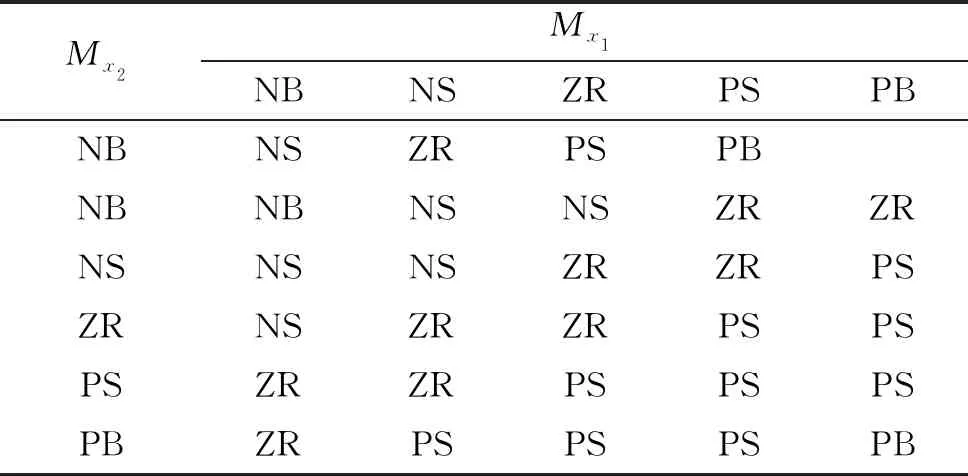
表3 x3模糊變量為ZR時y的模糊規則表

表4 x3模糊變量為PS時y的模糊規則表

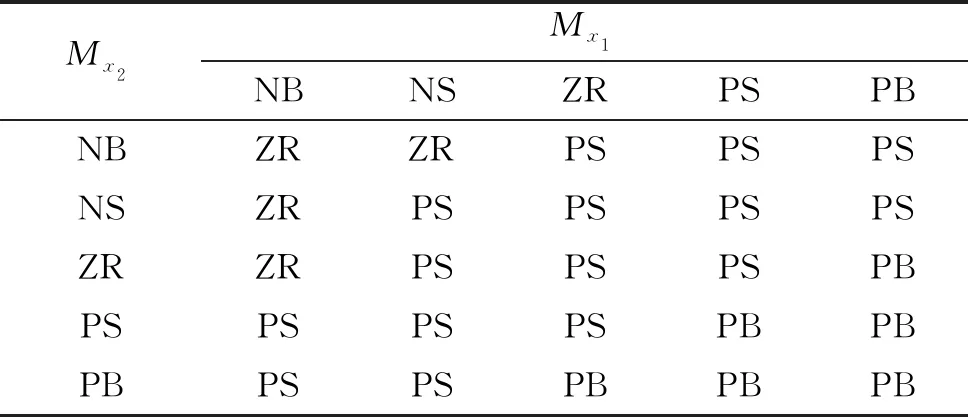
表5 x3模糊變量為PB時y的模糊規則表

3)最近鄰聚類算法設計模糊系統

首先把第一對輸入輸出數據當作聚類中心，然后選取一個預定值r，以區別接下來的數據和已有的聚類中心是否在同一個聚類里面。用乘積推理、單值模糊器、中心平均解模糊器和高斯隸屬度函數構造模糊系統，具體算法為：

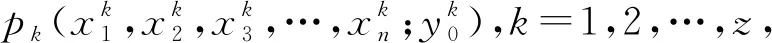
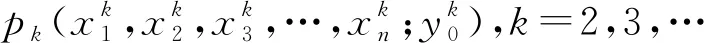
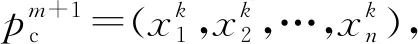
如果|pk-pi|≤r，則

(55)

(56)

當l≠lk,l=1,2,…,m時，令:

(57)

(58)

第三步：令k=k+1,返回第二步。

第五步：采用乘積推理，單值模糊器，中心平均解模糊器和高斯隸屬度函數構造模糊系統為:

(59)

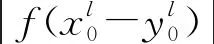
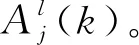
4 仿真驗證

為了驗證基于最近鄰聚類算法的模糊動態面控制器的控制效果，在Simulink中對其進行仿真實驗[8]。針對同一信號，分別采用傳統PID控制和一般動態面控制與文中設計的控制器來進行對比。

該控制器作用的破障武器的調炮轉角為0°～60°，穩態誤差要求在±0.05°，并且要求滿角度調炮時間要小于5 s。 在仿真中，選擇階躍信號和正弦信號作為控制器的輸入[9]。

4.1 階躍信號輸入

隨機選擇30°的階躍信號作為輸入，仿真的時間為5 s,圖4為仿真結果。

圖4 階躍信號響應曲線

可以看到，傳統PID到達穩態用時為3.6 s,最大超調量為9.8°；一般動態面控制到達穩態用時為1.6 s,最大超調量為4.5°。而采用最近鄰聚類算法的動態面模糊控制到達穩態用了0.8 s，幾乎無超調，穩態誤差在±0.01°。相較于前兩種控制器，無論是到達穩態時間還是超調量都有顯著改善。

4.2 正弦跟蹤

為了進一步比較控制器的性能，選擇正弦信號作為輸入，該信號周期為2 s,幅值為30°。圖5～圖7為仿真結果。

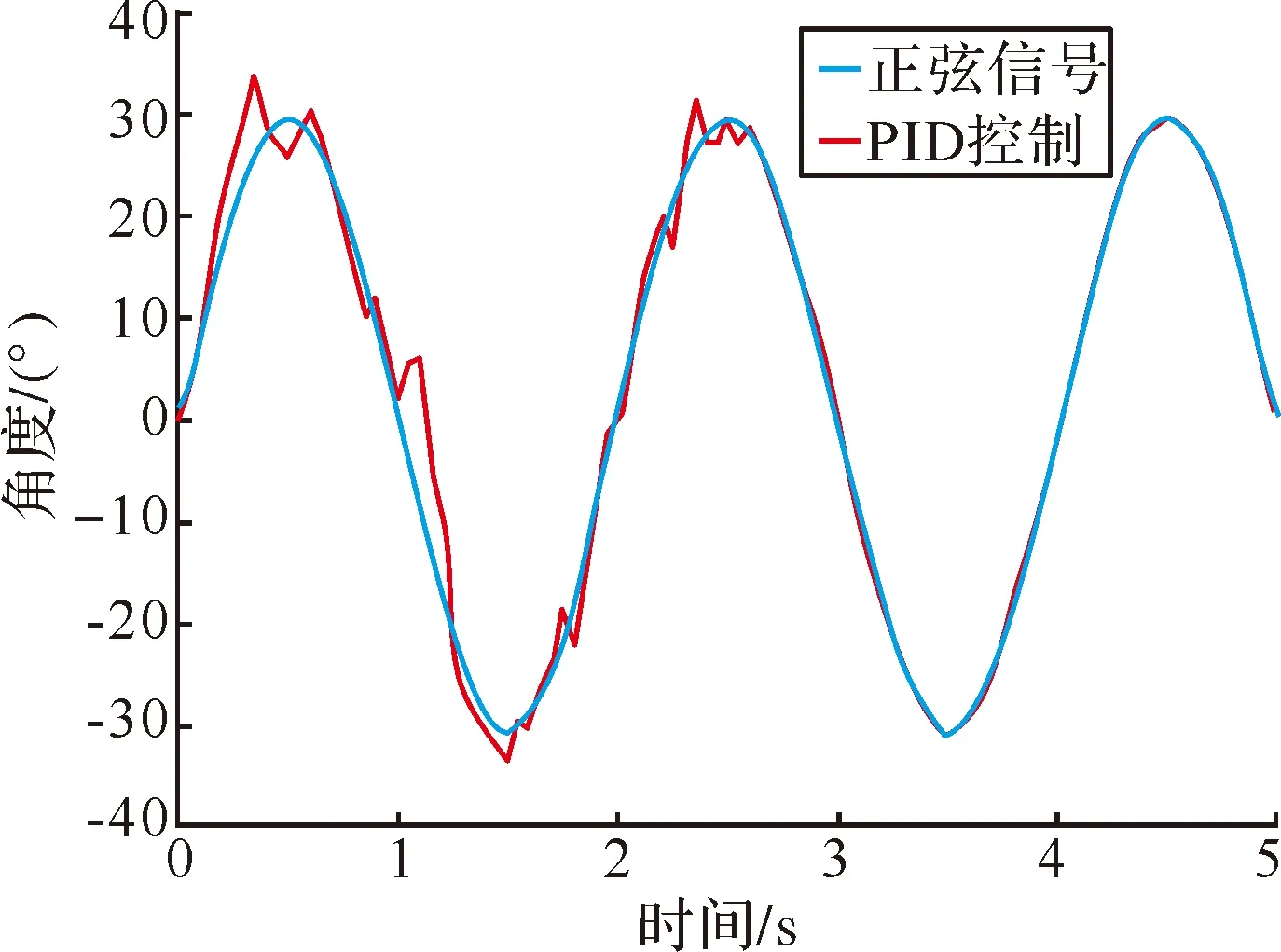
圖5 PID正弦跟蹤曲線

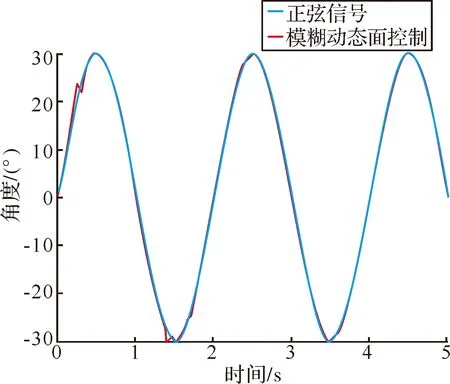
圖7 模糊動態面正弦跟蹤曲線

從圖中可以看出傳統PID和一般動態面控制跟蹤正弦信號所花時間分別為3 s和1.5 s,明顯大于基于最近鄰聚類算法的模糊動態面控制的0.5 s。同時最近鄰聚類模糊動態面控制器的誤差在±0.01°左右，滿足系統要求。

綜合上述的仿真結果，基于最近鄰聚類算法的模糊動態面控制器在相同信號輸入作用下，相較于其他兩種控制器作用下具有更小的跟蹤時間和跟蹤誤差。

5 結論

針對某破障武器電液伺服系統控制中存在的非線性和不確定問題，設計了基于最近鄰聚類算法的模糊動態面控制器。仿真結果表明，該控制器可以有效地解決上述問題，并且相比PID控制器和一般動態面控制器有著更好的控制性能。該控制器可以加快系統的響應速度并且提高調炮位置精度。