基于機器學習的可轉債定價與實證分析研究

牛曉健 巴雄

摘要：可轉換債券作為一種兼具債券和股票特征的金融產品，已成為資本市場重要的融資工具和廣大投資者青睞的資產配置工具。由于國內可轉債的附加條款及內含期權復雜，常用的Black-Scholes公式嚴格的前提假設往往造成定價結果偏差較大。經實證發現，以31個可轉債因子作為解釋變量，通過支持向量回歸能很好地擬合可轉債價格。

關鍵詞：可轉債定價;Black-Scholes模型;機器學習;支持向量回歸

中圖分類號：F832 文獻標識碼：A文章編號：1009 - 5381（2021）05 - 0058- 14

收稿日期：2021 - 08 - 02

基金項目：本文系國家自然科學基金面上項目“流動性壓力、信息交互與價格聯動——基于中國股票和債券市場多層復雜網絡的風險交叉

傳播機制與控制修復策略研究”（項目批準號：71873039，71573051）階段性研究成果。

作者簡介：牛曉健，男，新疆阿克蘇人，復旦大學國際金融系教授。研究方向：量化投資。

巴雄，男，江西九江人，復旦大學經濟學院金融碩士研究生。研究方向：量化投資。

一、引言

可轉換公司債券（以下簡稱可轉債）是指持有者可在規定時間內按照轉股價轉換為公司股票的債券，或者可以直接持有到期等待發行人還本付息。可轉債最早出現在美國金融市場，由于兼具債券價值的保底和復雜期權的波動機會，可轉債在發達的金融市場發展迅速。中國的可轉債市場起步較晚，發展歷程大致可以分為幾個階段： 第一個階段是21世紀之前。1993年，國內可轉債市場迎來了首個可轉債標的——由中國寶安集團發行的寶安轉債，發行規模為5個億。1997年，國務院證券委員會發布《可轉換公司債券管理暫行辦法》，這個階段是我國對可轉債的初步探索。第二個階段是2000-2004年。這期間相繼迎來了《上市公司發行可轉換債券的實施辦法》《關于做好上市公司可轉換債券發行工作的通知》兩大規范政策，市場上的可轉債標的數量達到兩位數，可轉債市場異軍突起。第三個階段是2005-2016年。這期間我國可轉債市場經歷了2005年的股權分置改革的一級市場停滯，隨后又逐漸恢復繁榮。在2015年股災期間，出現大幅贖回及發行停滯的現象，可轉債市場大起大落，規模尚小。第四個階段是2017年至今。2017年，國家進一步嚴格股票定向增發的要求，可轉債市場諸多利好政策出現，可轉債發行數量和發行規模大幅增加。近些年來，為解決中國再融資的結構失衡，監管層進一步完善了可轉債、可交換債的發行方式，為可轉債等再融資產品創造了良好的發展條件。

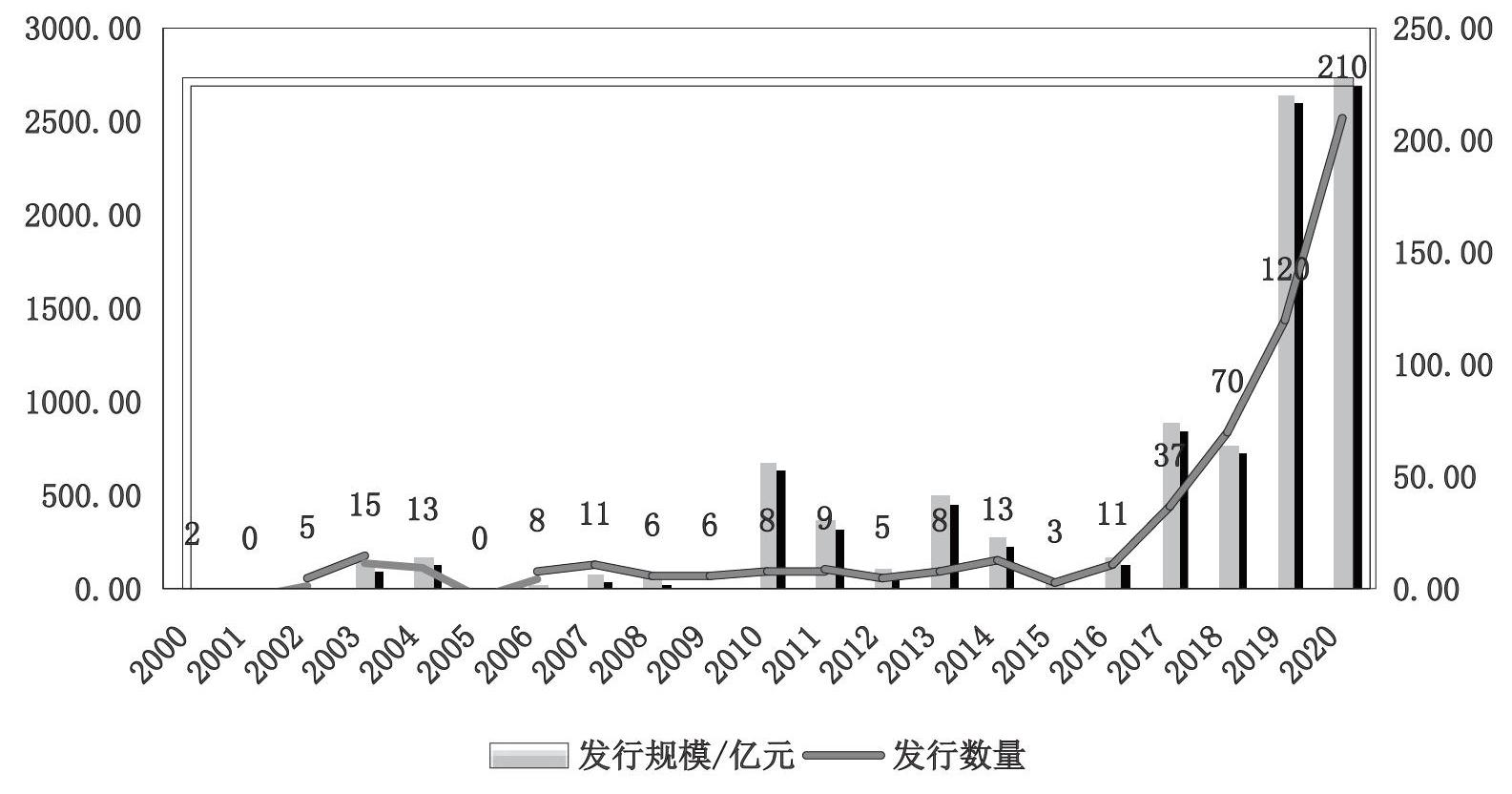
從圖1可以清晰看出2000年至今可轉債市場的變化，即隨著我國可轉債發行數量的增加，可轉債市場發行規模逐漸增加。其中，2019年發行規模2657億，2020年發行規模2736億，2020年發行數量210只。與此同時，可轉債存量達5434億。截至2021年3月19日，可轉債數量達374只。

圖1? 2000-2020年中國可轉債的發行情況

無論是從可轉債發行數量還是從發行規模來看，可轉債市場都已經進入快速發展階段，但由于可轉債條款設計的復雜性，加上投資者知識匱乏，導致可轉債暴漲暴跌及可轉債折價現象頻發，不利于我國可轉債市場的健康發展。因此，解決可轉債定價效率低的問題成為重中之重。一方面，合理的定價體系可以讓發行人有效地發行可轉債，制定內含的各種條款，尋找最優的融資方式;另一方面，正確的定價體系能幫助投資者準確地對可轉債價格進行估計，構建最優的投資組合。可轉債定價方法的探索不僅要借鑒國外經典的可轉債定價思想，更要從我國可轉債市場的特點出發，與時俱進，嘗試從更多歷史數據中挖掘對可轉債價格具有解釋力的信息。目前機器學習方法在國內金融市場中已有較多應用，且隨著可轉換債券投資性價比逐步提升，機器學習模型在可轉債定價領域更具可行性。

二、文獻綜述

（一）國外可轉債定價方法綜述

國外對可轉債定價的研究首次出現于1968年[1]，Weil以及后來的Baumol and Malkiel 等對可轉債的價格屬性展開討論，將可轉債的價格等價為未來選擇轉股后的股權價值，以及作為信用債持有到期的價值兩部分并進行貼現，取較高者作為當前轉債的合理定價。

其中BC為轉債價值，B為未來時點的信用債價值，S為未來時點的選擇轉股獲得的股權價值，r為折現率，t為未來時點距離當前的時間。

1970年，Black-Scholes期權定價公式的誕生使可轉債的相關研究開啟了新的篇章，模型認為可轉債價值包含了公司債券和若干份股票期權兩種金融工具的價值。B指的是可轉債的純債價值，OP是轉股期權的價值，B為每期現金流貼現之和，其中為每期現金流，為信用價差，為無風險利率。OP由Black-Scholes公式算得，其中K為轉股價格，股價歷史波動率為δ，可轉債期限為T：

Brennan and Schwartz[2]認為，可轉債價值只由服從幾何布朗運動的公司市場價值決定，從而基于Black-Scholes公式和風險中性定價思想，推導出偏微分方程，結合最優贖回策略和最優轉換策略確定微分方程的邊界條件求解。Ho and Pfeffer[3]在定價中引入了利率的波動。Goldman Sachs[4]首次將可轉債的信用風險引入定價模型，綜合股價的波動與信用風險的調整給出可轉債定價方法。Longstaff and Schwartz[5]提出了最小二乘蒙特卡羅模擬法（Least Squares Monte Carlo Simulation，簡稱LSM），該方法假設正股未來波動符合幾何布朗運動，在模擬生成大量可能的正股價格序列后，便可以采取類似于二叉樹的逆向推導方法，借助最小二乘估計逐步推算前一期轉債的期望持有價值，最后對各條模擬路徑的轉債估值結果取平均值，從而得到轉債在當前時點的理論定價。Dubrov and Bella[6]曾提出強化學習算法可以比蒙特卡洛模擬更好地找到最優執行策略，基于大量的實證研究和數值實驗，發現若引入二叉樹的計算，機器學習模型將更有效。

（二）國內可轉債定價方法綜述

自從我國第一只轉債（寶安轉債）上市后，國內開始出現可轉債定價的實證分析。具有代表性的為鄭振龍教授在2004年提出的風險中性定價法，通過贖回條款及轉換條款確定邊界條件，通過數值解法解得可轉債價格。鄭振龍、林海[7]率先指出，可轉債的定價復雜性主要表現在是否執行期權以及何時執行期權，由此產生的問題可以歸納為：

1.附加條款的期權為奇異期權，很難得到其解析解;

2.轉股期權為美式期權，很難以蒙特卡洛模擬;

3.內含期權多為路徑依賴期權，難以使用二叉樹和有限差分法等數值方法。

如圖2所述，可轉換債券的價值由股票價格和債券價值決定，假設股票價格服從幾何布朗運動：

可轉債視為股票的衍生品，可轉債的價格偏微分方程可表示為：

江良、林鴻熙、林建偉及宋麗平[8]基于隨機利率模型對可轉換債券定價分析，結果顯示利率的隨機波動對可轉債價值具有影響。王茵田、文志瑛[9]基于Tsiveriotisand Fernandes信用風險的定價模型，發現考慮修正條款后，模型的精度明顯提高且可轉債溢價現象有所改善。馬林、黃中翔[10]采用偏最小二乘回歸方法，選取了對可轉債具有解釋能力的變量，并分類為轉債、正股及指數類因子，結合最優停時定理給期權定價。程志富、胡昌生[11]構建了基于套利限制的可轉債交換期權模型，基于遠期風險中性測度以及期權的超復制方法，并應用2015年2月至10月的可轉債數據進行驗證，提升了模型準確度。沈傳河等[12]基于改進的支持向量回歸算法，以鋼釩轉債為例，考慮了諸如正股價格、轉股溢價率等8個相關變量，進行支持向量回歸SVR訓練，并對203條數據進行測試，發現支持向量回歸模型的準確度最好。

以往文獻采納的定價框架大都基于嚴格的Black-Scholes公式前提假設，然而這些假設是我國金融市場無法滿足的。隨著機器學習模型的流行，機器學習模型的強大擬合能力以及函數優化的特征被慢慢挖掘，加之不斷充實的數據為模型提供了較強的支撐，使得模型精度及穩定性進一步提升。下文將嘗試用機器學習擬合的方法給可轉債定價。

三、可轉債價格影響因子及有效性檢驗

（一）可轉債價格影響因子

如圖3所示，當正股股價較低或平價小于面值100的狀態，可轉債價格貼近于債底價值小幅波動;當正股股價較高或平價大于面值100的狀態，可轉債價格貼近于平價或者轉股價值波動。其中，可轉債價格相對于債底或平價的溢價通常被解釋為轉債的估值變動。

價值分解也可以進一步用Black-Scholes公式求導來說明，可轉債價值CB同時由債底B、正股S及估值Vol驅動。在我國，還由可轉債的自身特有屬性決定（如附加條款等）。

我國可轉債市場的波動更多由可轉換債券對應正股的價值主導。對比2007年1月至2020年12月間中證轉債指數和滬深300指數凈值曲線，兩者波動方向基本一致，說明轉債漲幅主要依賴于對應正股的驅動力，見圖4。

在我國轉債市場內，由于幾乎無法低成本對沖，可轉債的價值根本在于正股，轉債大多以轉股的方式退出轉債市場。此外，雖然債底價值占據大部分的比例，但帶來的波動卻是股遠大于債。因此，正股類驅動力實證部分重點關注轉債對應正股的營收能力、盈利能力、現金流情況及資產負債結構，同時也應綜合考慮對應正股的規模、估值及所處的行業等因素。

債底價值在可轉債價值中占比較大，但純債價值的波動對于可轉債價值的影響較小。一是國內可轉債的面值接近純債價值;二是若債底價值因出現了利好而明顯上升，機會成本增加，投資者不會因此去投資可轉債。

本文從債底價值計算公式出發，考慮票面利率、債券面值、貼現率、補償利率及現金流貼現率，應用可轉債評級對應同時期中債企業債收益率作為分母的現金流貼現率。

轉債價格相對于其債底價值和轉股價值的溢價被投資者稱為可轉債的估值，實際投資中常用純債溢價率和轉股溢價率來衡量。估值指標大小也決定了可轉債是偏股性還是偏債性。本文采取轉股溢價率及純債溢價率兩類指標分別衡量轉債的股性和債性。

自身屬性和附加條款類因子，主要考慮可轉債是否進入了贖回、回售期，這點可從公司發布的強制贖回或強制回售公告中獲取，是否進入了下修期能從可轉債規定的轉股價格來反映。自身屬性主要從債性評級、中簽率、所處生命周期等因子來考慮。

本文從可轉債的正股影響因素、債底計算公式、估值因子及附加條款歸納總結了對轉債價格有解釋力的31個因子，如表1所示。經過因子數據的去極值及標準化處理后，對因子進行分層回測檢驗。各部分因子在后續實證過程中都統一為日頻，未更新的日期采用最新的數據填充。數據均可從Wind獲得，缺失率不高，因子覆蓋度較好。

（二）因子分層回測及檢驗

分層檢驗常用于股票多因子策略中因子有效性的檢驗部分，目的是通過在每一個橫截面將不同因子的截面數據進行分層。如果不同層因子的表現有顯著區別，則證明該因子對轉債的收益率具有解釋力度。具體操作步驟如下：

1.選取2019年1月-2020年11月期間有交易數據的可轉債標的，一共85只可轉債標的和433個交易日數據;

2.因子每一周按數值從小到大排列分成五層，在這一周內分別持有排列在每一層的轉債，設置交易費用萬分之三，下一周按此規則換倉;

3.在區間內每周換手一次，最后得到每層的一個收益率序列，并畫出每層轉債的累積收益率曲線。

需要說明的是，因子的表現可能在某些時段分層效果較好，有些時段分層不顯著。該現象可能由可轉債市場風格變動等原因導致，我們認為這類因子對價格仍具有一定解釋力度。另外，由于截面數據量較少，容易出現單層數據少，可能給分層結果帶來偏差。

如圖5所示，轉股溢價率因子在測試區間段內分層效果較明顯，反映出轉股溢價率是一個不錯的估值因子，回測區間內呈現較好的單調性。低轉股溢價率的轉債累積收益率越高，一定程度上印證了可轉債的低價格低溢價率策略，即“雙低”策略在我國轉債市場投資中表現較好。

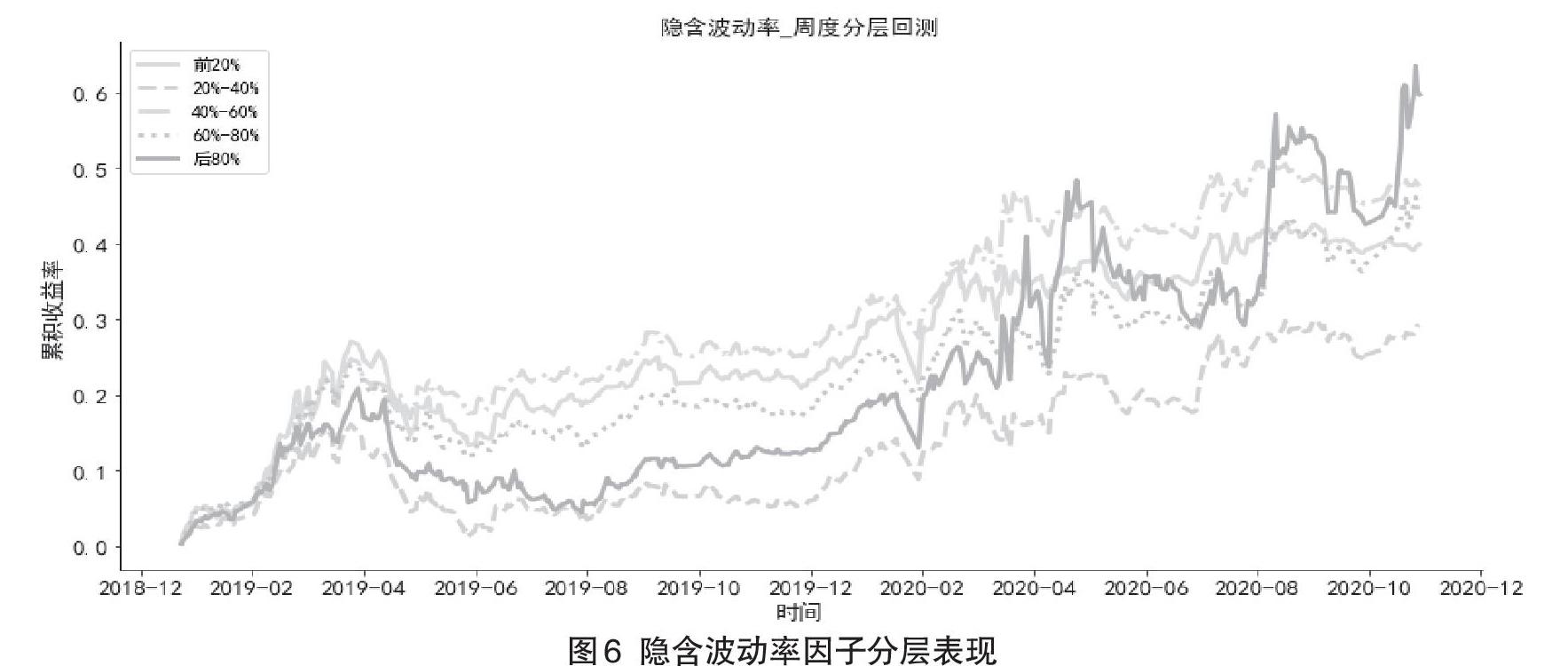
圖6中，隱含波動率因子分層效果較為理想，意味著通過隱含波動率來挑選可轉債，長期看來具有一定的穩定性和正向收益。隱含波動率的單調性表現較好。

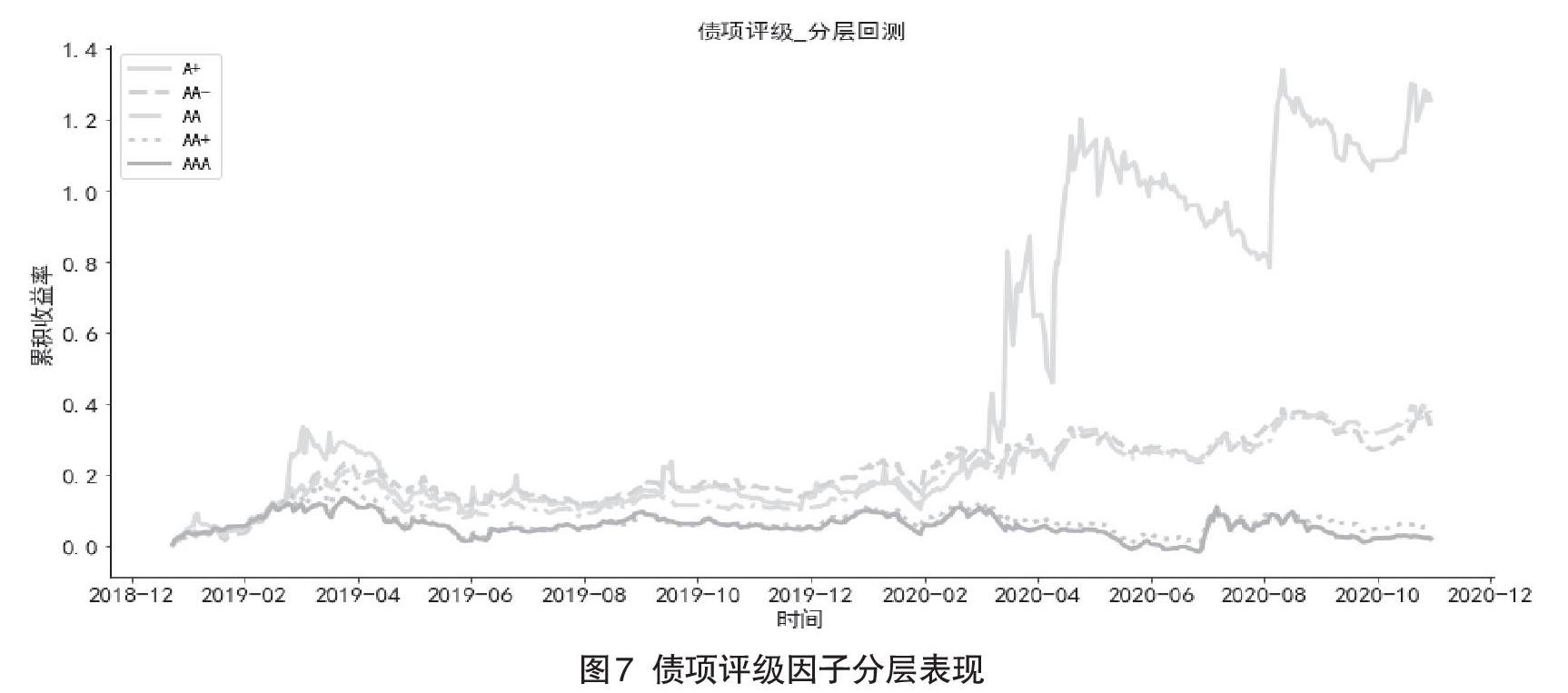
圖7中，可轉債的債項評級效果也較好，高評級債券累計收益率波動更小，收益也相對較低。相對來說，低評級債券展現出更大的波動，也有更高的收益。這是因為低評級債券的正股雖然市值小，但彈性更大，且低評級的轉債規模也相對更小，更容易出現彈性更大的情況，所以在2019年和2020年大盤環境好的時候，容易出現價格迅速上升的現象。

圖8中，可轉債的對應正股股價日波動率分層明顯且單調性較好，表明正股波動率越大，可轉債累積收益越高，這在2020年表現尤為明顯。這也印證了波動率越高、可轉債的內含期權價值就越大、可轉債價值越高的這一規律

四、機器學習介紹及支持向量機理論

（一）機器學習模型定價優勢

從可獲取的可轉債歷史數據的寬度及深度、定價模型的優劣及模型的假設條件來看，應用機器學習模型的優勢在于：

1. 我國的可轉債市場在存量和增量上，目前均有足夠歷史數據支持機器學習模型的訓練和驗證。同時，隨著機器學習理論的不斷深化應用，國內外開始出現基于復雜的數學模型給轉債定價的實證分析。未來我國可轉債市場有效性有望增強，一些轉債交易亂象產生的數據噪聲也將逐漸變少。

2. 現有的可轉債定價理論大多基于Black-Scholes框架，考慮的因素多為Black-Scholes公式中的影響因素，比如股價、波動率、利率及執行價格（轉股價格），未考慮估值因子（轉股溢價率等）和正股的基本面表現。

3. 我國金融市場不滿足Black-Scholes理論中股價符合幾何布朗運動以及期權可對沖復制的兩點假設，且市場賣空機制還有待完善，造成Black-Scholes定價結果的偏差。相比之下，支持向量機回歸模型不需要局限于這些假設，更多的是通過對輸入的解釋變量和被解釋變量關系的訓練，找出之間的函數關系。不可忽略的是，通過支持向量機回歸（SVR）模型難以計算出衡量可轉債內含期權的敏感性的字母，而這正是Black-Scholes模型的理論優勢所在。

（二）支持向量機理論

支持向量機SVM（Support Vector Machine）是一個數學理論嚴格完備的模型，可以用來解決分類問題（Support Vector Classify）和回歸問題（Support Vector Regression）。支持向量機有較高的擬合準確率，在非線性、小樣本及高維模式方面都具有比較明顯的優勢，常用來解決非線性分類問題及回歸問題，通過改變核函數及其參數可以調試不同的預測效果，是目前應用最廣泛的機器學習方法之一。本文主要介紹實證過程中涉及的支持向量機回歸的思想及解法。

機器學習模型與普通最小二乘線性回歸方法最大的區別就是損失函數。只有在輸出結果與真實數據之間的差距超過一定值ε時，機器學習模型才會計算損失，并給予對應的懲罰系數。

如圖9所示，如果訓練樣本的輸出結果滿足時，是實際結果，則認為輸出結果沒有損失;如果訓練樣本的輸出結果滿時，則需要計算模型的損失并給予懲罰。進而，支持向量機回歸問題可表示為如下優化問題：

其中，損失函數前的系數C被稱為正則化常數，當模型訓練時結果與真實數據差距較大，則需要通過懲罰機制使模型訓練結果趨于起初設定的目標。C也為懲罰系數，是不敏感損失函數，表達式如下：

損失函數的理解亦可直觀表示為圖10。

在損失函數的基礎上，引入松弛變量和，且將落在左右兩側的松弛程度設置不一樣，支持向量回歸問題可表示為：

然后，引入拉格朗日乘子，得到上式的拉格朗日函數：

令對偏導數為零，并結合，可得：

此問題下KKT條件如下：

由上式得，當且僅當為0，可不為0。已知約束條件與不能同時為0，所以，至少有一個為0。

將偏導數為零的條件之一，代入可得SVR解形式如下：

使的樣本即為支持向量回歸的支持向量，該樣本必落在ε間隔帶外即，由KKT條件可求出，則由下式可求b，一般都會取多個滿足的樣本，得到b的平均值。

另外，可以將上述解寫成特征映射形式，即可將SVR的解析解如下式，為核函數。

五、可轉債定價實證

（一） 數據獲取處理

數據來源：本文實證所需的所有數據，轉債價格序列及轉債因子數據都來自Wind金融終端及Tushare Pro平臺。

數據時間段選取：本文選取2015年1月1日至2020年12月31日間所有交易數據不為空的轉債標的，一共383只轉債，包括中途退市轉債。價格序列是該時間段的日頻交易數據，每個轉債從其上市日期起至2020年12月31日。因子數據從價格序列的時間點獲取，一共1531個截面數據，根據前文分析，總共提取四大類因子，31個基礎因子。

數據條拼接及數據集劃分：因子數據與當日的價格序列對齊。非日頻的因子及非時間序列的因子遵循最近原則。日期未公布的數據采用日期最近的數據填充。在拼接的所有價格因子數據條中，每月隨機選取一個交易日的數據作為模型的測試集，并在剩下的數據中每周隨機選取一個交易日作為模型的訓練集數據，訓練集數據與測試集數據不存在相同的數據條。

數據預處理：國內轉債市場頻繁出現暴漲暴跌的現象，以及因子缺失的數據條的處理對實證結果都有很大影響。主要步驟如下：

1.轉債價格數據進行處理：去除成交量為0的數據，成交量為0大多數是轉債遭遇停牌，本文認為當天價格并未反映最新的信息，予以剔除。

2.國內可轉債市場存在少數規模較小的債券，T+0的交易規則下容易被少數持有者操縱交易，存在日內漲跌幅巨大的標的，嚴重偏離可轉債的理論價值。因此，剔除單日漲跌幅絕對值超過20%的數據條。

3.對轉債因子數據進行處理：因子數據數量級不一致時，直接輸入模型會造成模型結果失效。因此進行標準化處理，即減去均值再除以標準差，方便后續同一量綱分析。

4.拼接數據，處理好價格數據及因子數據后，每月隨機選取一個交易日的數據作為模型的測試集，并在剩下的數據中每周隨機選取一個交易日作為模型的訓練集數據，最終得到訓練集數據21000條，測試集數據5800條。

（二）Black-Scholes模型實證結果

Black-Scholes模型廣泛用于可轉債定價領域，鄭振龍和林海[7]將可轉債的贖回條款作為微分方程的上邊界，下修條款作為下邊界，使用蒙特卡洛模擬和顯性有限差分方法進行求解，結果顯示當時我國的可轉債市場價格都存在低估，并將此歸因于當前的市場無效。但Black-Scholes方法并非完全適用于國內市場，蔣殿春、張新[13]很早之前指出Black-Scholes公式定價可轉債內含期權是不準確的，并另外提出二項分布模型對可轉債進行定價，以正股股價為主要驅動因素，并兼顧各項附加條款對可轉債價值的影響，提高了模型定價的精度。

Black-Scholes模型中分別計算可轉債的純債價值和轉股期權價值。純債價值為可轉債的各期現金流貼現值，貼現率使用對應期限對應評級中債企業債到期收益率;轉股權價值等于內含轉股期權的價值，等于轉換為股票的份數乘以單個期權的價值，單個期權是以正股為標的資產，轉股價為執行價格的看漲期權。具體計算步驟如下：

其中，為可轉債現金流，取當日日期未來的現金流，即現金流發生日大于當日日期;為純債貼現率，應用對應企業債收益率，這里選用中債指數收益率;為（現金流發生日-當日日期）/365;

為正股股價，為轉股價格，為可轉債剩余期限，σ為波動率，即正股過去一年的歷史波動率，無風險利率為，這里采用一年期國債收益率。

Black-Scholes公式是目前運行穩定性最高的方法，理論意義強，能清晰刻畫出轉債價值的框架，且可以用來計算轉債的瞬時敏感系數，但Black-Scholes公式存在將債券與期權相割裂的缺陷，也無法刻畫回售贖回等諸多復雜條款。

此部分基于Black-Scholes模型的步驟，應用python進行實現，定義計算期權價值函數C（S，X，R，T，σ ）和債底價值函數C（Ci，R，T），對經過數據處理后的5800條測試集數據的價格進行測算，并通過計算以下指標觀察Black-Scholes定價的效果：

1.平均絕對誤差MAD，模型理論價格與市場價格的誤差的絕對值的平均數;

2.平均絕對誤差偏離度，絕對誤差占市場價格的比例的平均值;

3.誤差的標準差，觀察兩序列之間的誤差是否穩定，衡量模型是否穩定;

4.誤差大于0的比例，衡量Black-Scholes方法是否存在一直高估或者一直低估的狀態。

Black-Scholes模型定價結果如表3所示，定價結果與市場價格誤差的絕對值平均值為10.26，平均百分比誤差為8.14%，精確度有所欠缺，但模型價格走勢方向與市場價格基本一致。進一步來看，百分比誤差的標準差較小，模型誤差較穩定，不存在一直明顯高估或者低估的情況。Black-Scholes模型可轉債定價的精度有待提高，穩定性表現尚可。

（三）支持向量回歸可轉債定價

SVR可轉債定價部分：輸入變量為t日的31個因子數據，輸出變量為t日的可轉債理論價格，計算與t日的實際市場價格誤差及誤差的表現，并與前文Black-Scholes定價結果進行對比，觀察定價的準確度及穩定性。

SVR價格預測部分：輸入變量為t日因子的前五日滾動均值，輸出變量為t日的預測價格，計算模型在測試集上的誤差。

在構建實證模型前，對核函數的選擇及核函數參數的選擇及遍歷空間有以下說明：

第一，支持向量回歸核函數選擇。學者魏瑾瑞[14]指出，支持向量機中的核函數是為了簡化計算，不同的核函數具有比例很高的共同支持向量、存在相似性。因此在某種程度上，核函數參數的選擇比核函數的選擇更加重要，選定核參數最少的高斯核僅涉及gamma參數及模型自身的懲罰系數C。本文實證數據解釋變量、訓練數據測試數據條都較多，選取適用性最廣的非線性核函數——高斯核函數，也稱rbf核。高斯核相比于線性核，可以選擇參數進一步優化，對于大樣本和小樣本均有比較好的性能，且對數據中存在的噪聲具有較好的抗干擾能力。另外，高斯核相比于多項式核的參數較少。

第二，核函數參數設置。得出最優參數組的兩種常見方法為窮舉法和固定乘積法，其中為給定的常數。窮舉法需要消耗更多時間及計算機算力，后者則能確定一個最優參數區，較為高效。本文結合及固定參數倍數的方法，確定不同的實證參數組合。參數γ意味著原始數據映射到高維數據后的分布，γ值的大小決定了分隔邊界的彎曲程度。γ值過小，模型擬合度可能較低;γ值過大，對極端值也形成擬合，存在過度擬合。懲罰系數C一般為模型的敏感參數，衡量的是模型對損失樣本的容忍度。

第三，輸入數據。選取2015年1月1日至2020年12月31日間有交易數據的轉債標的，一共383只轉債，其中包括中途退市轉債。價格序列是該時間段的日頻交易數據。因子數據從價格序列的時間點獲取，一共1531個截面數據。根據前文分析，總共提取31個因子。數據處理后最終得到訓練集數據21000條，測試集數據5800條。

第四，參數敏感性分析。選用高斯核（RBF核）作為支持向量回歸的核函數，有兩個敏感性參數：C和γ。C為懲罰系數，默認設置為1，如果樣本噪音較多，可將懲罰系數的初始值設置較小。γ為核函數參數，決定了樣本映射后的分布。

第五，確定對參數的遍歷空間。懲罰系數取C∈{0.05，0.1，0.5，1，5，10}，核函數參數取γ∈{0.0005，0.001，0.005，0.01，0.05，0.1}，兩種參數組合一共有36種組合，在觀察不同參數組合的絕對誤差百分比、標準差及均值的表現情況，反映模型準確率的同時，也可以反映模型對參數的敏感性情況。這里將分別記錄不同參數組合下，訓練集及測試集上模型的表現，觀察模型的穩定性。

依照上述步驟將訓練集輸入模型進行訓練，得到模型后再輸入測試集的31個轉債因子，計算輸出價格與測試集真實市場價格的差距，計算各項評價指標。支持向量回歸SVR可轉債定價結果如表4至表6所示：

從SVR模型的效果來看，綜合表4、表5、表6三個指標的表現，表現最好的參數組合為C=10， γ=0.001。該參數組合下測試集的絕對誤差百分比為1.98%，標準差為2.01%，絕對誤差均值為2.49，意味著在經過21000條訓練集數據訓練后，在5800條測試集上的測算精度達到98.2%。預測精度較高，誤差表現穩定，說明模型在經過充分訓練后預測結果較為精確，可信度較大，定價結果較為精確。

另外，從參數敏感性來看，懲罰系數C相對核函數參數γ更加敏感，懲罰系數C默認參數為1。當懲罰系數C小于1時，懲罰系數越小，無論是在訓練集還是測試集上，模型誤差變大且波動也大，模型的精度及穩定性表現都不理想，這說明模型存在欠擬合;當懲罰系數大于1時，模型的總精度表現總體較優，但此時若γ值稍大，則模型在訓練集上表現較好、測試集上表現不好，說明模型的核函數參數在0.01以上時，高斯核的特征邊界彎曲度較大，模型存在明顯的過擬合。核函數參數在0.01以下，γ敏感性明顯降低，此時不會隨著參數的改變模型的結果發生較大變化。

表7總結對比SVR和Black-Scholes定價實證分析，雖然支持向量回歸模型對數據的深度廣度要求更高、求解過程更耗時，但綜合考慮模型的精確度及穩定性，支持向量回歸模型給可轉債定價的效果更加準確，模型穩定性更好。隨著未來國內可轉債市場逐漸規范化，機器學習模型有望在可轉債定價理論實際投資領域得到進一步發展。

從圖11、12中可看出，SVR方法得到的百分比誤差更小、表現更穩定。綜合表格中評價指標的表現及誤差的波動情況，SVR誤差99.10%都集中在10%以內，模型更精確。支持向量回歸能大概率將定價誤差控制在10%以內，相比Black-Scholes模型能提取出對價格具有解釋力度的因素。

六、結論與建議

本文嘗試應用支持向量回歸定價國內可轉債。從可轉債價值的四大驅動力出發總結了31個因子，并同時給予邏輯解釋和分層回測檢驗，分析其影響作用。為了形成對照，本文先基于Black-Scholes公式對可轉債的轉換期權和債底價值定價得到可轉債價值，并進一步運用支持向量機回歸方法擬合可轉債價格，觀察與Black-Scholes定價效果之間的差異。

本文應用支持向量回歸做了兩步實證：第一步是在所有的訓練集和測試集上實證，確定懲罰系數為10，核函數參數0.001，輸入變量為31個因子，輸出結果為可轉債的理論價格。結果顯示SVR模型誤差的各項指標均大幅優于Black-Scholes定價方法。第二步是基于大量的訓練集數據，選取的10只可轉債的歷史時間序列價格進行預測，發現支持向量回歸SVR依然能很好預測單個轉債的下一日價格，模型預測價格能為可轉債的市場價格提供參考。

綜上，以上述31個因子作為輸入數據，通過支持向量回歸方法能很好地擬合出可轉債價格，得到一個較為滿意的可轉債二級市場定價模型。在實際投資過程中，可以先結合因子選出具有投資價值的可轉債標的，并支持向量回歸的理論價格給出買入時點建議，形成自上而下先擇券再擇時的投資策略。

參考文獻：

[1]ROMAN，L，WEIL，et al. Premiums on Convertible Bonds[J].The Journal of Finance，2012，23（3）：445-463.

[2]SCHWARTZ M.CONVERTIBLE BONDS：VALUATION AND OPTIMAL STRATEGIES FOR CALL AND CONVERSION[J].Journal of Finance，1977，32（5）：1699-1715.

[3]THOMAS S Y，HO，DAVID M，et al. Convertible Bonds：Model，Value Attribution，and Analytics[J]. Financial Analysts Journal，1996，（52）：35-44.

[4]GOLDMAN SACHS. Valuing Convertible Bonds as Derivatives[J].Quantitative Strategies Research Notes，1994，（11）：1-30.

[5]LONGSTAFF，FRANCIS A. Valuing American options by simulation：a simple least-squares approach[J].Review of Financial Studies，2001，14（1）：113-147

[6]DUBROV B. Monte Carlo Simulation with Machine Learning for Pricing American Options and Convertible Bonds[J].Available at SSRN，2015.

[7]鄭振龍，林海.中國可轉換債券定價研究[J].廈門大學學報（哲學社會科學版），2004（2）：93-99.

[8]江良，林鴻熙，林建偉，等.基于隨機利率模型可轉換債券定價分析[J].系統工程學報，2019，34（1）：57-68.

[9]王茵田，文志瑛.向下修正條款對中國可轉債定價的影響[J].清華大學學報（自然科學版），2018，58（1）：108-112.

[10]馬林，黃中翔，劉天昀，等.可轉換債券定價和實證研究[J].金融經濟，2020（8）：82-86.

[11]程志富，胡昌生.杠桿交易限制下可轉債的交換期權定價模型[J].管理工程學報，2020，34（1）：195-199.

[12]沈傳河，劉中文，李纓.基于改進SVM的可轉換債券價值分析與套期保值[J].系統管理學報，2016，25（1）：22-27.

[13]蔣殿春，張新.可轉換公司債定價問題研究[J].國際金融研究，2002（4）：16-22.

[14]魏瑾瑞.對支持向量機混合核函數方法的再評估[J].統計研究，2015，32（2）：90-96.

Research and Empirical Analysis of Convertible Bond Pricing Based on Machine Learning

Niu Xiaojian，Ba Xiong

（Fudan University，Shanghai 200433，China）

Abstract：As a financial product featuring both bonds and stocks，convertible bonds have become an important financing tool in the capital market and an asset allocation tool favored by the majority of investors. However，due to the complexity of the additional terms and options of domestic convertible bonds，the strict assumptions of Black-Scholes formula often lead to a large deviation in the pricing results. The empirical results show that the 31 convertible bond factors summarized in this paper are taken as explanatory variables and the price of convertible bond can be well fitted through support vector regression.

Key words：convertible bond pricing;Black-Scholes model;machine learning;support vector regression