基于顆粒阻尼的U肋加勁板減振降噪初探

孔德睿，張 迅，劉子琦，游穎川，鄭寧哲，周靖翔

（西南交通大學 橋梁工程系，成都610031）

鋼箱梁因其結構簡單、造型美觀、環境適應性強等特點，在城市軌道交通、高速鐵路的橋梁建設中逐漸得到應用。然而，鋼箱梁在受到車輛沖擊時產生的噪聲具有頻譜寬、幅值大、控制難等特點，是當前亟待解決的問題。

現有研究表明，輪軌噪聲和橋梁結構噪聲是軌道交通噪聲的重要來源。目前，輪軌噪聲已經得到了較好的控制[1]，但針對橋梁結構噪聲的控制研究較少。目前較為成熟的橋梁振動控制方法為設置調諧質量吸振器(Tuned mass damper，TMD)和敷設約束阻尼層(Constrained layer damping，CLD)。但TMD只能針對特定頻段減振，CLD存在易老化、適應性差等缺點。為此，本文基于顆粒阻尼(Particle damping，PD)原理，提出一種用于鋼箱梁減振降噪的新方法。鋼箱梁噪聲來源于幅面尺寸較大的板件的局部振動[1-2]。U 肋加勁板是鋼箱梁的典型板件，且U 肋具有天然的空腔，這為填充顆粒提供了便利。為此，本文首先對組成鋼箱梁的U肋加勁板進行考察。

顆粒阻尼技術的基本原理是將顆粒填充至主體結構空腔內，主體結構振動引起顆粒運動，通過顆粒與顆粒、顆粒與腔壁間的摩擦與碰撞耗散能量[3]。國內外學者陸續提出了顆粒阻尼器的各種簡化模型或數值分析方法。Friend和Kinra[4]將顆粒阻尼器簡化為一個質量塊，采用實測阻尼考慮顆粒運動帶來的阻尼效應。胡溧等[5]建立了顆粒阻尼器的粉體力學模型，并研究了顆粒容器參數對減振性能的影響。吳成軍等[6]引入氣體-顆粒兩相流理論，在與有限元法結合后，提出了一種考慮顆粒阻尼的結構振動預估方法。近年來，離散單元法[7](Discrete Element Method，DEM)被廣泛應用于研究顆粒運動問題，該方法可以考慮顆粒間及顆粒與容器壁間的相互作用，為多顆粒運動的模擬提供了更準確合理的方法。例如，楊英等[8]基于DEM研究了填充顆粒的尺寸、數量、材料等參數對減振效果的影響。武宏程等[9]基于穩態能量流法和DEM進行了顆粒阻尼器仿真，獲得了耗散功率效率、有效動態質量和等效黏性阻尼系數等物理量，并開展了試驗驗證。

因顆粒阻尼結構簡單、作用頻譜寬、適應性強等特點，其在機械、航空航天領域得到了廣泛應用。例如，Koch 等[10]將顆粒阻尼和蜂窩結構結合后，應用于發動機的減振降噪。王林玉[11]將顆粒阻尼器應用于列車車輪的噪聲控制，實測1 600 Hz～5 000 Hz的徑向及軸向噪聲分別降低了16.28 和14.74 dB(A)。Jie等[12]采用錘擊試驗驗證了顆粒阻尼對鋼軌的減振效果，并建立了模擬鋼軌與顆粒物非彈性碰撞的解析模型，討論了激勵力、顆粒材質、顆粒質量對減振效果的影響。在土木工程領域，關于顆粒阻尼的相關研究仍處于初步階段，且主要集中在抗風、抗震等領域。例如，Lu 等[13]對設置顆粒調諧質量阻尼器(Particle Tuned Mass Damper，PTMD)的框架結構在不同地震激勵下的振動特性進行了數值模擬和試驗研究。結果表明，PTMD 在較寬頻帶內表現出顯著的阻尼效果。Yan 等[14]通過縮尺試驗對比研究了地震作用下懸索橋的動力響應。結果表明，添加顆粒阻尼后，結構的位移峰值響應和加速度均方根響應都有較大幅度降低。然而，交通荷載激勵下的橋梁振動行為與地震、風等作用時有較大區別。因此，將顆粒阻尼技術應用于鋼箱梁車致振動噪聲控制的可行性還有待論證。

本文介紹一種基于顆粒阻尼的鋼箱梁減振降噪新方法。以鋼箱梁U 肋加勁板為研究對象，通過錘擊試驗和數值仿真手段研究設置顆粒阻尼試件的振動噪聲特性，對比分析不同顆粒填充質量、填充位置對減振性能的影響規律。在此基礎上，采用數值仿真進行噪聲預測。本文的分析方法和研究結論可為今后進一步開展鋼箱梁減振降噪優化設計提供參考。

1 試驗方案

1.1 試驗裝置

基于錘擊試驗原理[15]，本文對填充顆粒阻尼的U肋加勁板縮尺模型進行了振動測試。試驗采用力錘(型號：LC1301B)對板件進行激勵，用加速度傳感器(型號：LC0108T、LC0102T)測量振動響應。為避免邊界條件帶來的不確定性影響，采用彈性繩將板件懸吊在自行設計的固定支架上，試驗裝置如圖1所示。

圖1 試驗裝置

1.2 縮尺試件

以實際工程中的典型鋼箱梁為原型，以1:4為幾何縮尺比制作了鋼箱梁U肋加勁板模型。模型基板為一1 200 mm×1 000 mm的鋼板，通過焊接與U肋進行連接。基板厚度為3 mm，U 肋厚度為2 mm。其他詳細尺寸如圖2所示。

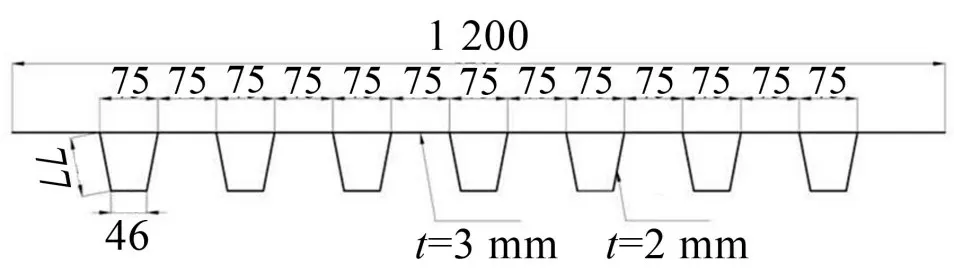
圖2 模型尺寸

1.3 測點布置

為測試板件各點的振動響應，在板邊緣區域選擇3 個激勵點，分別位于板件短邊的1/4、1/2、3/4 長度處。加速度傳感器設置在每個U肋間隔區域的幾何中心，即板件長邊56.25 mm、225 mm、375 mm、525 mm、675 mm、825 mm、975 mm、1 143.75 mm 位置處。測點位置及編號如圖3 所示。圖中，三角形表示加速度傳感器的位置，箭頭表示錘擊位置。

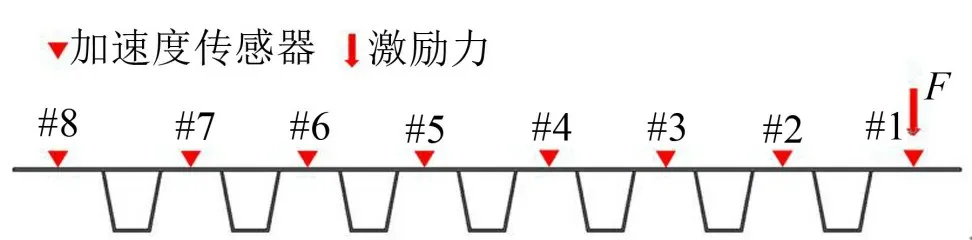
圖3 頻響試驗的測點布置

為分析填充顆粒帶來的阻尼效應，需要測量板件的平均振動響應。如圖4 所示，將板件按照U 肋單元分為15個矩形區域(R1,R2,R3,…,R7及8個U肋間隔區域)，在各區域隨機選取3 個位置作為激勵點，即在15個區域共設置45個激勵點。在圖示位置設置加速度傳感器，測量每次錘擊時的振動響應。根據互易性原理，可求得板件的平均振動響應。

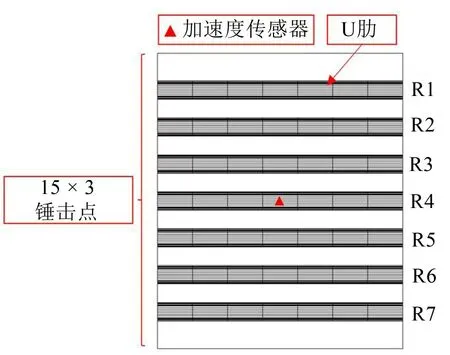
圖4 阻尼損耗因子試驗的測點布置

1.4 測試工況

為初步探索不同參數下的減振性能，在U 肋中填充不同質量和不同分布位置的顆粒。在實際應用中，顆粒阻尼器作為附屬結構，其總質量不宜過大，否則會對橋梁承載能力產生影響。依照經驗以加勁板質量的10%為上限，采用直徑5 mm 鋼珠進行填充，試驗照片見圖5。填充率最大時，顆粒體積約占U 肋空腔體積的5%，其對U 肋加勁板強度、疲勞等的不利影響基本可忽略。

圖5 試驗照片

具體工況如表1所示。表中質量填充率為顆粒總重量與原加勁板總重量的比例。所示填充位置Ri(i=1,2,…,7)與圖4中標注的U肋編號一致。

表1 試驗工況

2 評價指標

2.1 頻響函數

通過力錘對板件進行激勵，采集錘擊力作為輸入信號，同時采集加速度響應作為輸出信號。由于每次錘擊的激勵力不同，為便于對比，采用頻響函數描述振動響應的大小。頻響函數由輸入信號與輸出信號的互譜及輸入信號的自譜求得[16]，即：

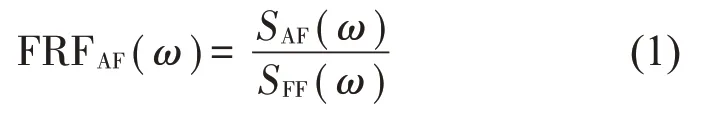
其中：SAF(ω)是輸入信號和輸出信號的互譜；SFF(ω)是輸入信號的自譜；ω表示頻率。

2.2 能級差

對于U肋加勁板，在噪聲考察頻段范圍，可將每個測點布置區域（即U 肋間隔區域）視為一個子系統。若其中一個子系統被激勵，子系統間的能級差可由下式確定[17]：

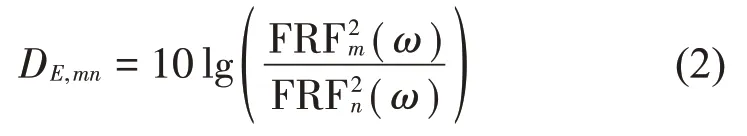
其中：DE,mn表示激勵子系統m和響應子系統n之間的能級差；FRFm(ω)為激勵子系統m的頻響函數，FRFn(ω)表示響應子系統n的頻響函數。

2.3 阻尼損耗因子

阻尼損耗因子是描述結構自由振動衰減特性的重要指標。為對比不同顆粒填充情況下結構的振動衰減情況，引入能量法求解阻尼損耗因子[18]，表達式如下：

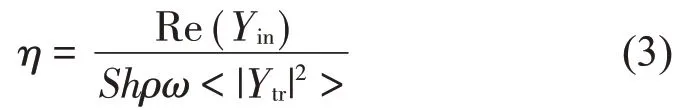
其中：η為阻尼損耗因子；Yin為驅動點導納；<|Ytr|2>為空間平均的均方傳遞導納；ρ為材料密度；h為板厚；S為板件面積。

3 試驗結果分析

3.1 填充質量的影響

保持顆粒填充方式為均勻填充7 條U 肋，分別對質量填充率為0（不填充）、5%、10%（對應表1中的工況L7M0、L7M5、L7M10）的加勁板進行錘擊試驗，得到試驗結果如圖6所示。

圖6(a)和圖6(b)給出了不同填充質量下，#3 和#5 測點的加速度頻響函數。對于#3 測點，頻響函數峰值在填充顆粒后下降非常明顯，其它頻率處也有不同程度的下降。對于#5測點，由于到激勵位置的距離較遠，填充顆粒后振動已經衰減到很小，導致工況L7M5和L7M10的頻響函數值差異不大。

圖6(c)給出了#1和#7測點的能級差，其中，#1測點處為激勵位置。能級差在填充顆粒后顯著增大，即振動隨距離衰減加快，在125 Hz、315 Hz附近最為明顯。填充率為5%～10%時，能級差平均增大約2 dB。

圖6(d)對比了阻尼損耗因子的變化。阻尼損耗因子在填充顆粒后變大，說明設置顆粒阻尼有利于振動更快衰減。各頻段阻尼損耗因子平均提高至原結構的2倍～2.5倍。其中，在80 Hz以上頻段，填充顆粒后的能級差和阻尼因子均顯著增大，說明顆粒阻尼具有一定的頻變特性，這與其它研究中的結論基本一致。

綜合上述對比，與工況L7M5 相比，雖然工況L7M10 的顆粒填充質量增加了一倍，但其減振效果并未得到顯著提升（僅略微增加），這可能是由于顆粒在大量填充后發生堆積而未能充分振動引起的。

3.2 填充位置的影響

對于填充位置的對比，保持質量填充率10%不變，分別測試均勻填充7 條U 肋、間隔填充4 條U 肋（對應表1 的工況L7M10、L4M10）下板件的振動響應，測試結果如圖7所示。

圖7(a)和圖7(b)給出了不同填充位置下，#3 和#5測點的加速度頻響函數。與原加勁板相比，兩種填充方式都能起到顯著的減振效果，總體規律與圖6(a)和圖6(b)相似。

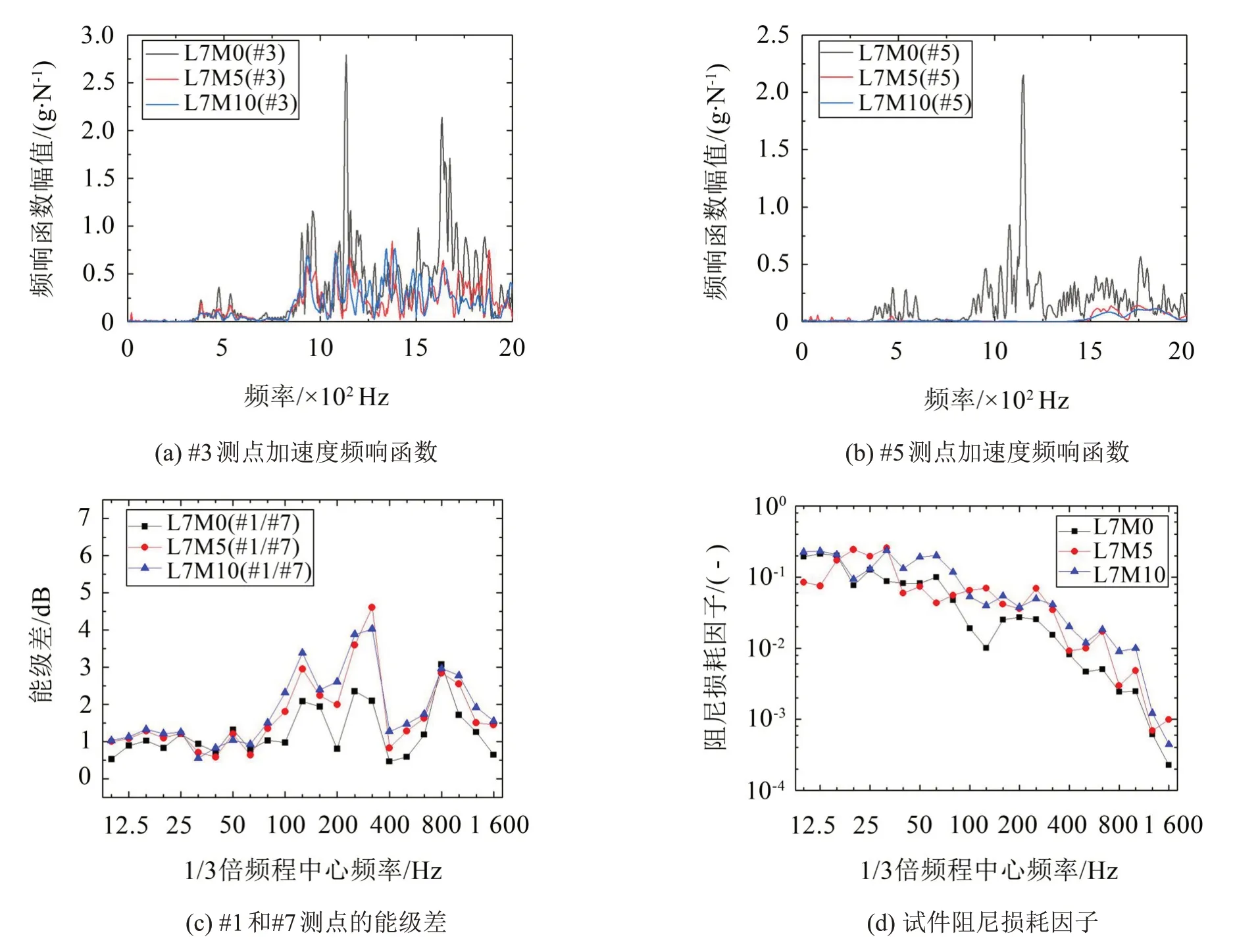
圖6 不同填充質量對減振效果的影響

圖7(c)給出了#1和#7測點的能級差。填充顆粒后的能級差在80 Hz 以上頻段顯著增大，在200 Hz處最為明顯，增大了約2 dB。在125 Hz和315 Hz等個別頻段，均勻填充的減振效果略好于間隔填充。

阻尼損耗因子的測試結果如圖7(d)所示。在315 Hz 以上頻段時，均勻填充方案的阻尼損耗因子略大于間隔填充方案。

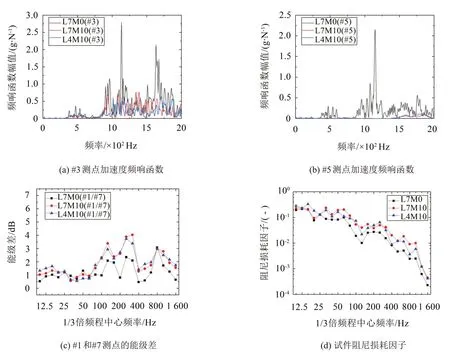
圖7 不同填充位置對減振效果的影響

總的來說，兩種填充方案均能增大能級差和阻尼損耗因子，但差異并不顯著，這可能是由于兩種填充方案都以均勻布置為原則，而質量填充率不變。

4 數值仿真分析

4.1 模型驗證

本文采用混合有限元-邊界元法進行振動噪聲預測。首先，在模型試驗的基礎上，根據實際縮尺模型尺寸，采用ANSYS 軟件建立有限元模型。然后，計算其頻響函數，將數值計算結果與實測結果對比，驗證仿真方法的可靠性。

有限元模型如圖8 所示。其中，基板和U 肋均采用Shell181 殼單元模擬，共劃分6 885 個節點、7 050個單元。本文將填充顆粒簡化為質量塊，未考慮顆粒間通過碰撞和摩擦引起的阻尼效應。采用實測阻尼損耗因子對加勁板定義結構阻尼。

圖8 有限元模型

仿真與實測結果對比如圖9 所示。結果表明，總體上，仿真值與實測值吻合較好，兩者的頻譜特性一致，驗證了有限元分析模擬這一過程的準確性。但是，在個別頻率點，實測值與計算值存在一定差異，這可能是由于阻尼損耗因子測量誤差、顆粒模擬的簡化處理等原因引起的。

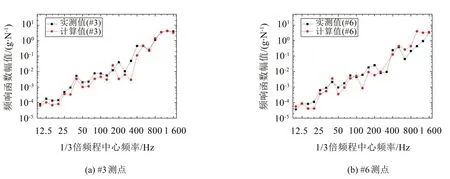
圖9 頻響函數計算值與實測值對比（工況L7M10）

4.2 噪聲預測

基于有限元計算得到的結構振動響應，采用邊界元法進行噪聲預測。由于實際工程中U肋位于鋼箱梁內部，箱體內的噪聲難以泄漏出去[19]，因此，計算時僅考慮基板振動所輻射的噪聲。將U肋加勁板的邊界網格導入LMS Virtual.Lab 軟件得到邊界元模型，如圖10 所示。其中，采用剛性反射面模擬地面聲反射效應，提取節點位移作為聲學計算的邊界條件。

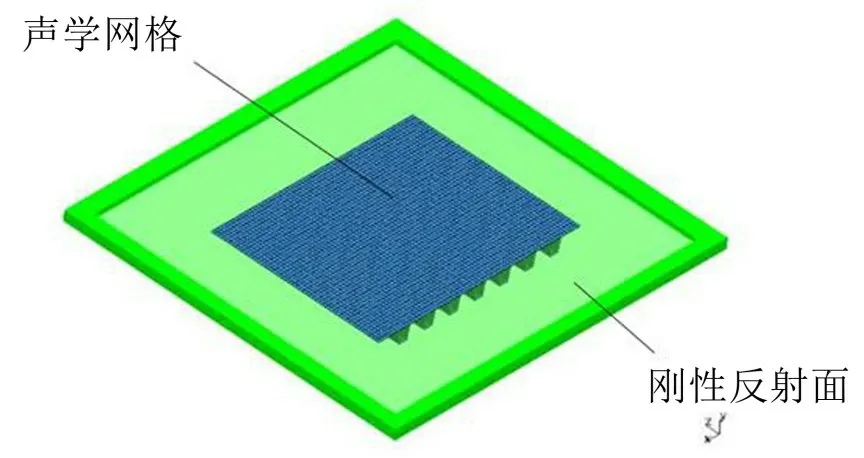
圖10 聲學邊界元模型

圖11 給出了4 種工況下的聲功率級。由圖可知，進行顆粒填充后，板件聲功率級總體上在不同頻段均表現為下降。其中，630 Hz處最為顯著，聲功率級降低了約13 dB(A)；在個別頻段（如1 250 Hz），板件聲功率級輕微增大，這主要是由于填充質量改變了加勁板的振動模態及不同頻帶的振動能量。

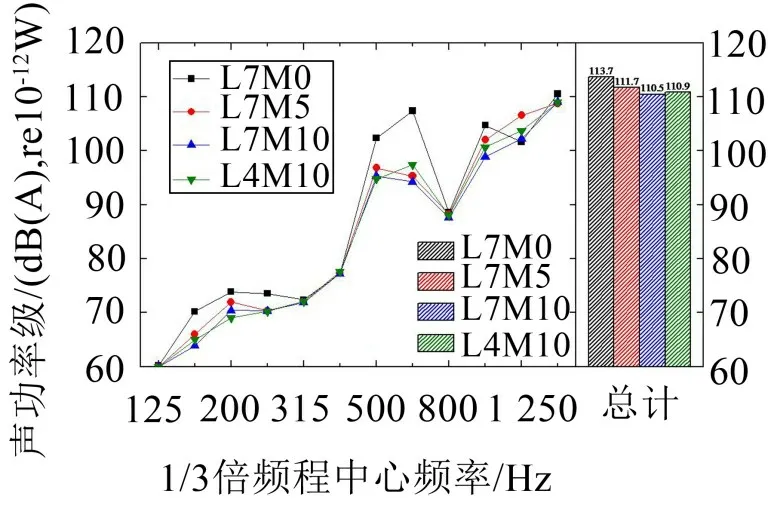
圖11 不同測試工況的聲功率級對比

質量填充率為5%時，板件各頻段的聲功率級均顯著減小，相比原始加勁板，總聲功率級降低了2.0 dB(A)。當質量填充率增至10%時，板件聲功率級進一步減小。在均勻填充和間隔填充下，總聲功率級分別降低了3.2 dB(A)和2.8 dB(A)。顯然，在質量填充率5%的基礎上，增加一倍的顆粒填充質量，并不能使降噪效果提升一倍，這與振動試驗得到的結論一致。對于不同填充位置，在500 Hz 以上頻段，均勻填充的降噪效果略好于間隔填充。

5 結語

（1）對于U肋加勁板結構，顆粒阻尼可以起到顯著的減振降噪效果，且作用頻帶較寬，具有工程應用前景。均勻填充10%質量時，各頻段阻尼損耗因子平均提高至原結構的2 倍～2.5 倍，總聲功率級降低了3.2 dB(A)。

（2）增加顆粒質量對減振效果有積極影響，本研究中10%填充質量的能級差和阻尼損耗因子略大于5%填充質量，但并未顯著增加。

（3）保持填充質量不變時，均勻填充和間隔填充兩種方案的減振效果未見明顯差異，但均勻填充方案在500 Hz以上頻段的降噪效果略好。

（4）顆粒阻尼的減振降噪效果具有一定的頻率相關性，但對減振和降噪的有效頻率并不一致。其成因有待進一步研究，這一現象同時也為顆粒阻尼的優化設計提供了思路。

本文針對鋼箱梁典型板件——U肋加勁板的顆粒阻尼減振降噪效果進行了初步探討，驗證了該措施的有效性。但是，當前所開展的測試工況較少，填充質量和填充位置的工況較為有限。今后，還需對顆粒材質、顆粒尺寸、顆粒分布、顆粒用量、顆粒容器設計等作進一步討論。此外，聲振分析中顆粒阻尼的精確模擬方法還有待深入研究。