橋面跳車沖擊過程下車-橋系統動力響應分析

楊 帆，劉修平，劉煥舉，黃綱領

(1.天水師范學院 土木工程學院，甘肅 天水741000；2.河北工程大學 土木工程學院，河北 邯鄲056038；3.中國公路工程咨詢集團有限公司，北京100097)

橋面跳車是車輛在通行過程中，由于橋面上障礙物的存在導致高差而使車輛發生起跳和沖擊的一種現象。跳車產生的沖擊荷載不僅會影響到橋臺、支座和伸縮縫等構造物的損壞，還會影響行車安全，引發交通事故[1-2]。因此，車輛跳車問題長期以來受到眾多學者和管養部門的廣泛關注[3-5]。

現有跳車研究大部分集中在成因分析和防治措施方面，部分研究中借助試驗手段研究跳車引起的橋梁沖擊系數變化及駕駛舒適程度[6-7]。蔣應軍等[8]歸納了路橋過渡段不均勻沉降類型并對成因分析，結合橋頭搭板設計方法提出了跳車綜合防治技術；潘曉東等[9]通過調查統計和駕駛行車實驗研究了跳車對駕駛舒適性的影響；龍關旭等[10]基于模型修正的單跨下承式混凝土系桿拱結構研究了行車速度和障礙物高度對橋梁跨中振動加速度的影響。試驗法雖然可靠、準確，但需人力、物力以及交通管制等費用的大量投入，開展成本較高，且難以獲取跳車沖擊過程中的車橋作用力變化的規律及駕駛員位置處的振動特性，因此，數值模擬法成為了研究跳車沖擊的主要手段。張麗芳等[11基于5 參數的車輛模型分析了行車速度及橋面沉降差對簡支橋梁沖擊效應的影響]；周子驥等[12]以1/4簡化的車輛模型和有阻尼簡支梁橋為對象，建立可模擬跳車沖擊過程的車橋耦合振動分析模型；樊建平等[13]考慮軌道周期和隨機不平順情況，研究了單軸車過簡支梁的跳車行為和動力特性。

由于車輛模型的建立以及車-橋耦合振動系統的求解在數學和力學上有一定難度，跳車沖擊過程中的車-橋系統動力響應分析多是基于單梁模型和簡化的車輛模型，研究結果對其他類型的車-橋系統參考價值有限。為此，本文基于21 自由度的4 軸整車力學模型和障礙物幾何模型建立跳車沖擊過程中的車-橋耦合模型，以4跨連續鋼桁橋為研究對象，分析跳車沖擊過程中的車-橋系統動力響應。

1 跳車過程中的力學分析模型

1.1 車輛動力模型

車輛動力模型的建立是車橋耦合振動分析的基礎，為了更好地反映車輛懸掛參數對車橋的動力特性的影響，車輛多被模擬為彈簧-阻尼-質量模型[14-15]。以4軸整車動力模型為例，圖1給出了所建立的整車動力模型，整個車輛可以分成9 個剛體部件：1 個車體、8 個車輪，車體具有豎向、橫向、點頭、側滾和搖頭共5個自由度，每個車輪具有豎向、橫向共2個自由度，因此，4軸8輪車型具有獨立自由度個數為21，整車的剛度、阻尼和質量矩陣可由達朗貝爾原理推導得到。

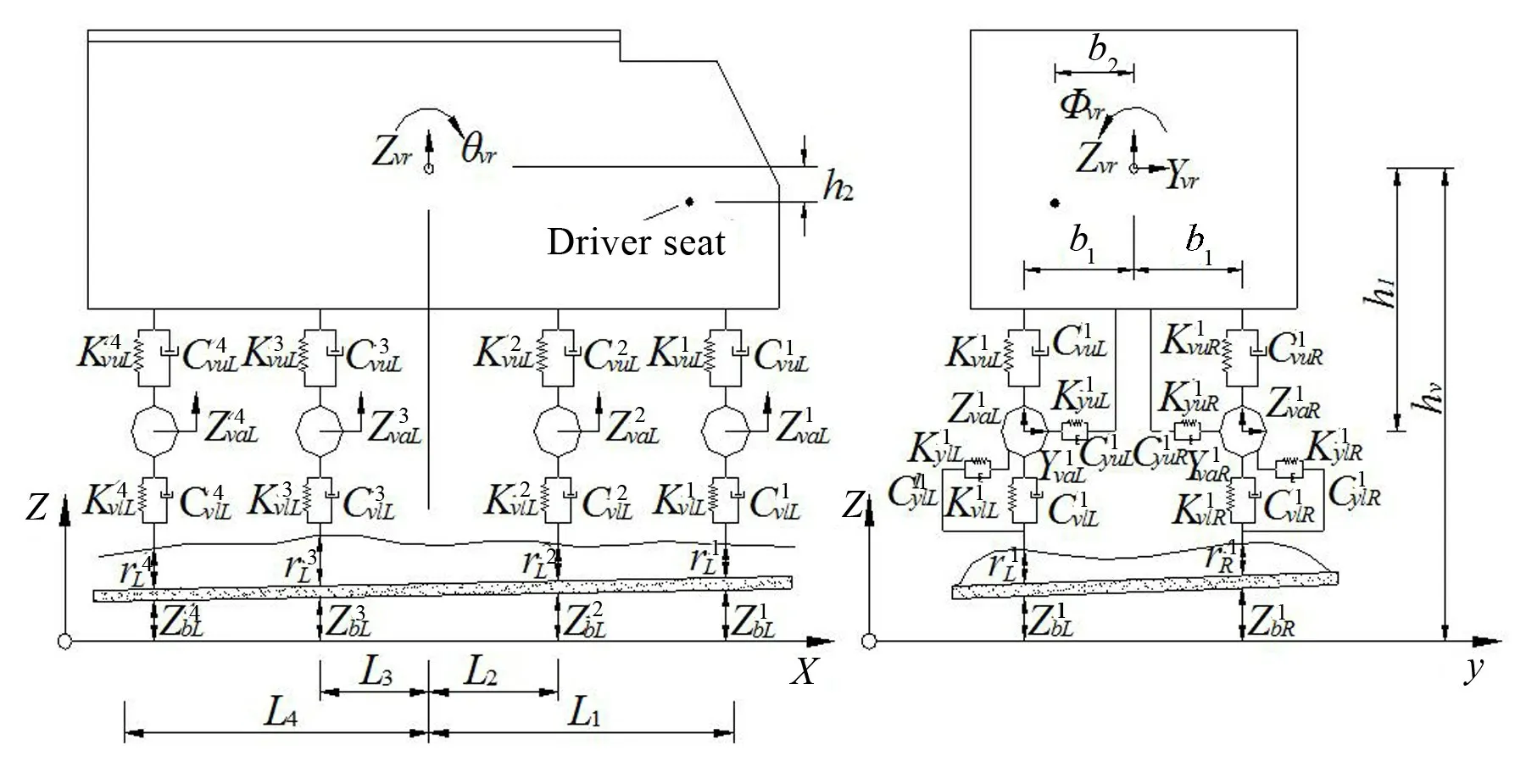
圖1 4軸整車動力分析模型

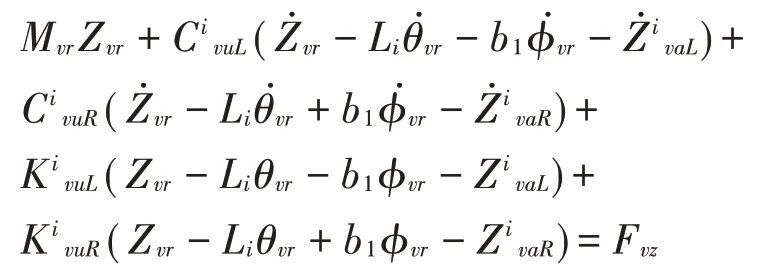
以z方向振動為例，1/2車體動力學平衡方程為：

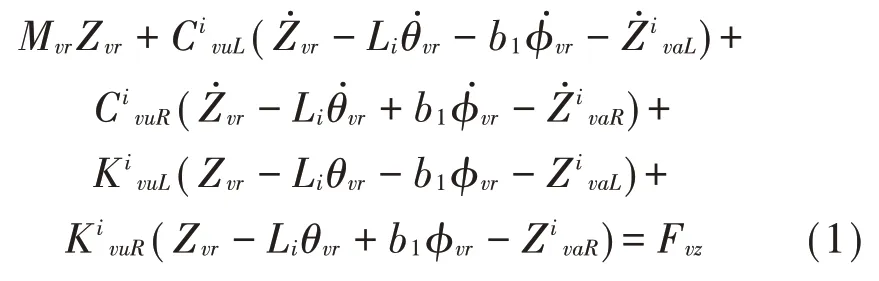
車輛左側車輪動力學平衡方程為：

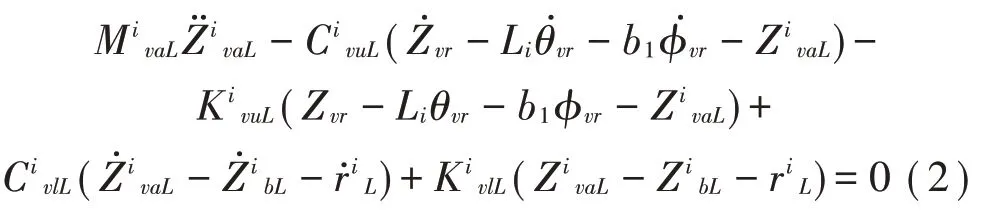
式中：i=1～4，為車輛軸數；KvuLi、KvlLi分別為第i個軸左側上、下層彈簧剛度；CvuLi、CvlLi分別為第i個軸左側上、下層彈簧阻尼；Zvr、Yvr、θvr、φvr、φvr分別為車體的豎向、橫向、點頭、側滾和搖頭位移；Li為第i個軸距離車體質心處的長度，ZivaL為第i個軸左側車輪的豎向位移；rLi和ZbLi分別為第i個軸左側車輪位置處的路面粗糙度和橋面處的豎向位移；Fvz為車體z方向所受的外載；Mvr為車體質量；MivaL為第i個軸左側車輪質量。

同理可推導車體及車輪其他方向的動力學方程，車輛模型中對應的懸掛參數的具體數值可依據《中國汽車車型手冊》和中國工業與信息化部頒布的《車輛生產企業及產品公告》確定。

1.2 障礙物幾何模型

障礙物模型采用公路橋梁荷載試驗規程(JTG/T J21－01－2015)[16]中所給出的障礙物信息建立橋面跳車障礙物幾何模型，以此作為橋面跳車行為的激勵源，幾何輪廓如圖2 所示。正常行駛段的車輛位移激勵由路面粗糙度提供[15]。在整個跳車過程中假設障礙物為剛體且不發生任何平動、轉動以及壓縮變形。則沿著車輛前進方向，障礙物提供的位移激勵和速度激勵分別為：

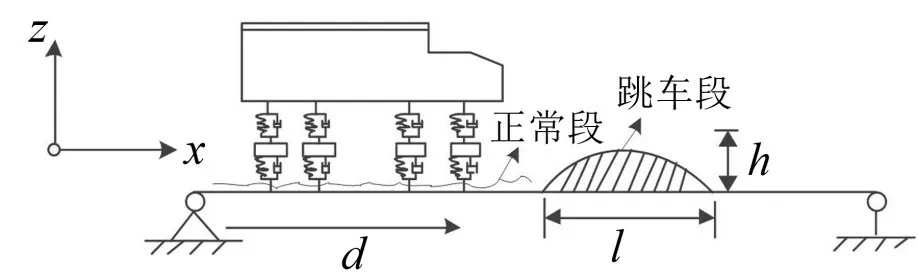
圖2 跳車過程中的車-橋耦合模型

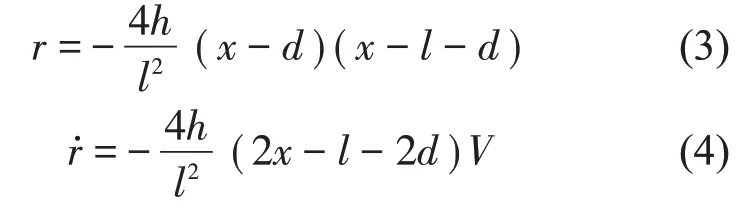
式中：r為路面豎向位移激勵˙為豎向速度激勵；x為車輪作用在障礙物上的縱向位置，d≤x≤d+l；h為障礙物最高點，距離橋面約為5 cm～7 cm；l為障礙水平長度，約為30 cm；V為行車速度；d為障礙物距離橋頭的長度。

2 車-橋系統耦合振動方程

2.1 力學耦合關系

根據結構動力學理論，車橋耦合系統的動力方程可表示為：

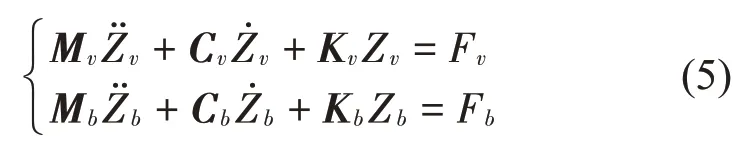
式中：M、K、C、Z、F分別為質量矩陣、剛度矩陣、阻尼矩陣、豎向位移以及車橋間的作用力，下標v、b分別表示車輛和橋梁子系統。

車輛行駛過程中，在車輪始終與橋面接觸的假設前提下，橋梁振動引起的橋梁豎向位移將引起車輛減震系統、懸掛系統的變形，路面粗糙度的存在也會引起車橋耦合體系運動形式的改變。因此，車橋間的作用力是關于車橋系統各自位移、速度、加速度以及外界激勵等變量的函數，當外界激勵源僅為路面粗糙度r時，車橋作用力表達為：

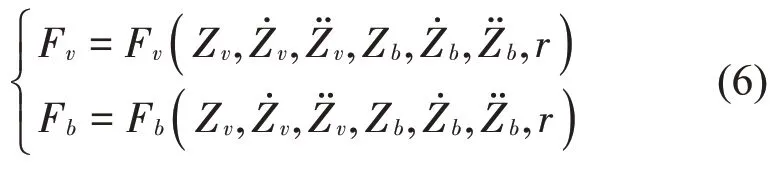
聯立式(5)與式(6)，可建立車輛與橋梁兩個子系統之間的力學耦合關系。

2.2 動力學方程求解

采用全過程迭代法將橋梁有限元模型和車輛模型分離以求解車橋耦合動力方程[17-18]。將路面粗糙度作為初始激勵，計算車橋作用力時程，將計算的車橋作用力時程輸入商用有限元軟件中進行橋梁運動狀態的求解，得到的橋梁運動狀態后配合插值系統獲取接觸點的位移和速度，并與路面粗糙度疊加作為新的激勵，再次計算車橋作用力時程，前后兩次的車橋作用力時程滿足收斂準則定時，可認為迭代終止。橋梁子系統的動力學方程由ANSYS求解，車輛子系統動力學方程通過newmarkβ法求解，迭代公式為：

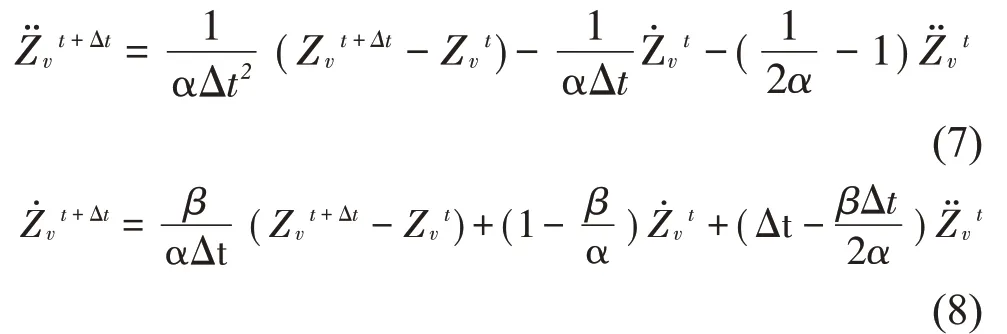
全過程迭代的優點在于延用了車橋分離迭代的思路，橋梁子系統的建模、計算和求解可在通用商業有限元分析軟件如ANAYS，ABAQUS 等中進行，耦合分析過程可以人為參與調控，及時控制更新。全過程迭代法的計算效率較時步迭代法高，一般進行少數幾步的迭代即可收斂，有研究表明[18]全過程迭代的求解次數僅為時步內迭代法的20 %～40 %左右。

2.3 適用性驗證

以某20 m 標準簡支T 梁為例開展跳車工況測試，以驗證所建立分析系統的適用性，結構標準斷面及有限元模型見圖3，有限元模型中采用Beam4 單元模擬主梁及虛擬橫梁，虛擬橫梁力學參數確定借助梁格分析理論，并基于靜載試驗數據對初始限元模型進行修正[19]。

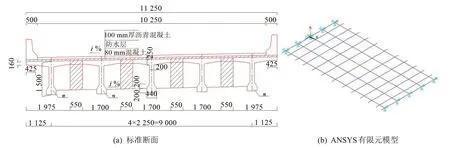
圖3 20 m 簡支T梁模型

跳車試驗過程中障礙物尺寸選擇兩種，即高度5 cm與高度7 cm，擺放位置均為橋梁跨中，采用30 t四軸車汽車作為試驗車輛，以5 km/h、10 km/h 和15 km/h的速度行駛過障礙物，同時采用加速度傳感器測試中梁跨中斷面加速度響應。

跳車過程中橋梁的結構動力響應觀測以豎向為主，限于篇幅，以5 cm障礙物5 km/h跳車工況為例，為有效減少高頻隨機噪聲與振動信號混合，對原始振動信號采用五點三次平滑法[20]分段進行處理，圖4為實測加速度時程與所建立分析系統分析結果的對比，圖中4 個加速度響應密集區域分別對應于車輛四個軸通過障礙物的瞬間。可見，0～7 s 內橋梁結構跨中豎向振動加速度很小，這是因為當橋面平整度較好，車輛行駛速度較慢時，橋上移動車輛荷載作用相當于擬靜力加載；7 s之后車輪駛過障礙物并跳車，橋梁跨中豎向振動加速度顯著增大。圖4 表明中梁跨中加速度實測結果與理論分析結果吻合良好。其它高度及車輛行駛速度下的計算加速度峰值和理論值的對比如表1所示。

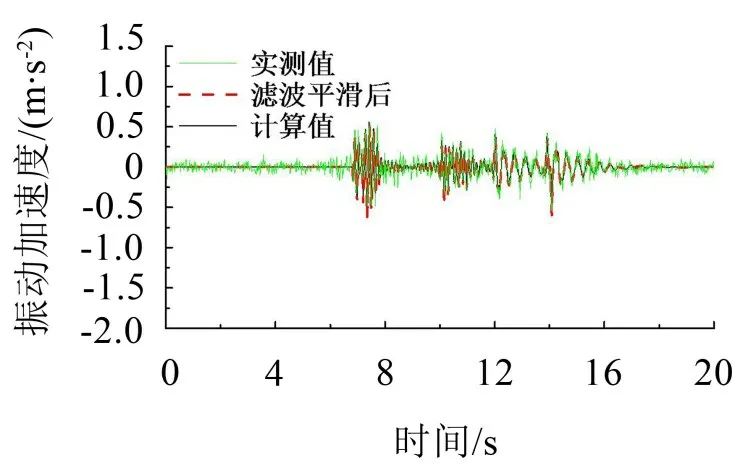
圖4 跳車過程中的豎向振動加速度曲線對比

表1 不同工況下的豎向振動加速度峰值

從表1可見，隨著速度和跳車高度的增加，除了部分點出現跳躍現象外，橋梁跨中豎向振動加速度的峰值隨之增大，且計算值和理論值的最大相對誤差不超過6%，說明所建跳車分析系統的適用性。

3 原型橋梁信息

為進一步研究橋面跳車過程下車橋系統的動力響應特征，以4 跨連續鋼桁橋為原型橋梁。橋面寬6.0 m，標準跨徑9 m，橋面系主體結構由厚度1 cm的Q235 鋼材路基箱組成，主體受力由8 片16 Mn 的貝雷梁承擔，底部橫梁由雙槽鋼搭接。考慮到薄壁箱截面存在翹曲與剪切變形的特性，縱、橫向桿件采用beam 188來模擬，其他豎、斜桿均采用link 10桿單元模擬。有限元模型如圖5，貝雷片上部與路基箱剛接，下部每隔9 m 與2 片槽鋼剛接，每片槽鋼底部設置3 個固定支座。將第1 跨跨中和第2 跨跨中上弦桿處設置為響應觀測點，研究跳車全過程中桿件應力和位移時程的變化情況。

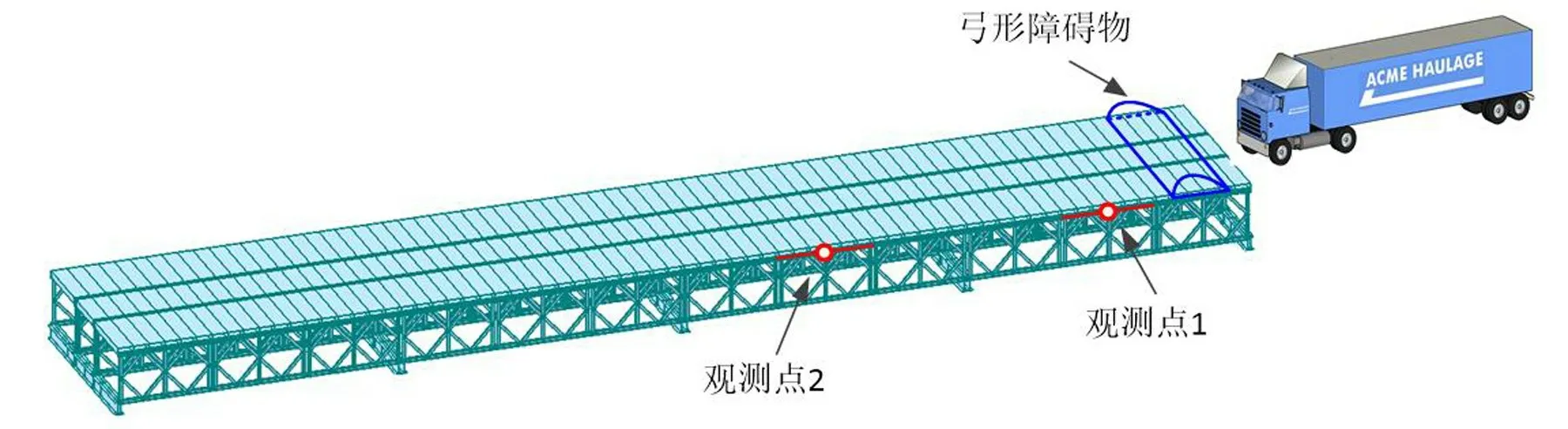
圖5 數值分析模型

4 跳車沖擊作用下車-橋系統動力響應分析

4.1 車橋接觸力時程

橋梁結構在橋頭伸縮縫或引道處常出現不均勻抬高或沉降現象，車輛駛過容易發生顛簸震蕩，將障礙物放置于橋頭作為跳車激勵源，研究車輛駛過障礙物時車-橋系統的動力響應特性。在路面粗糙度選取為“很好”的前提下，選取單車車速為20 km/h～50 km/h、車速步長為10 km/h的4種工況進行分析，限于篇幅，此處僅給出20 km/h的速度下，四軸車前、后輪的接觸力的時程，具體結果如圖4所示。

由圖6可知，在0～2.5 s時間段內，前輪(第一個軸)與橋面出現即將脫離的情況，前輪此時的接觸力接近于0，在后輪(第4個軸)通過障礙物之前，受前輪激勵的影響，后輪的接觸力浮動值約為1.2，后輪通過瞬間對前輪也產生了類似的影響。相比正常行駛，前、后輪接觸力浮動值分別約為2.2和2.1。說明在車輛駛過障礙物的過程中，車橋作用力變化劇烈，且車輛前后輪的接觸力相互影響。

圖6 車橋作用力時程

4.2 行車舒適性評價

當汽車以較大的加速度振動時，人的負荷強度也會迅速增加，因此，車輛座位處的加速度的幅值是衡量人心理生理負擔的重要指標[21]。行車舒適性指標一般分為7個等級，該指標計算公式[4]為：

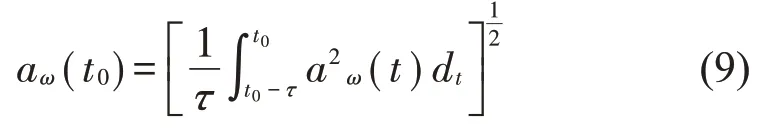
式中：aω(t)為瞬時加權加速度幅值；τ為持續平均積分時間，這里τ取1；t為時間積分變量；t0為瞬間時刻。

車輛最大瞬時振動加速度值(Maximum transient vibration value，MTVV)與駕駛舒適性的關系見圖7，以20 km/h車速為例，圖8、圖9分別為正常行駛、發生跳車時駕駛位置處的振動加速度時程。

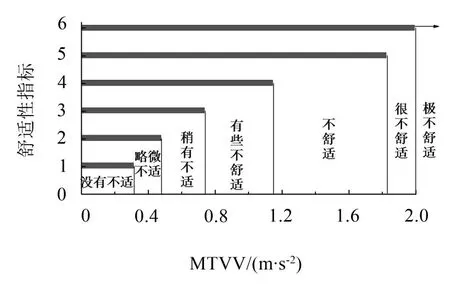
圖7 MTVV與舒適性關系

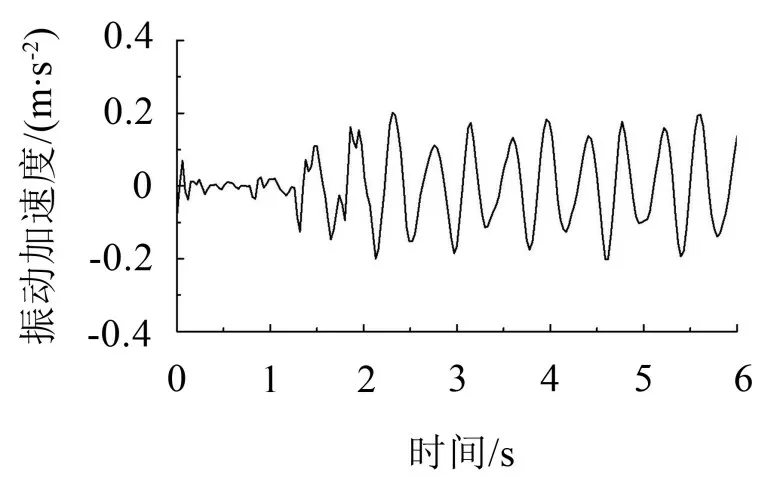
圖8 正常行駛

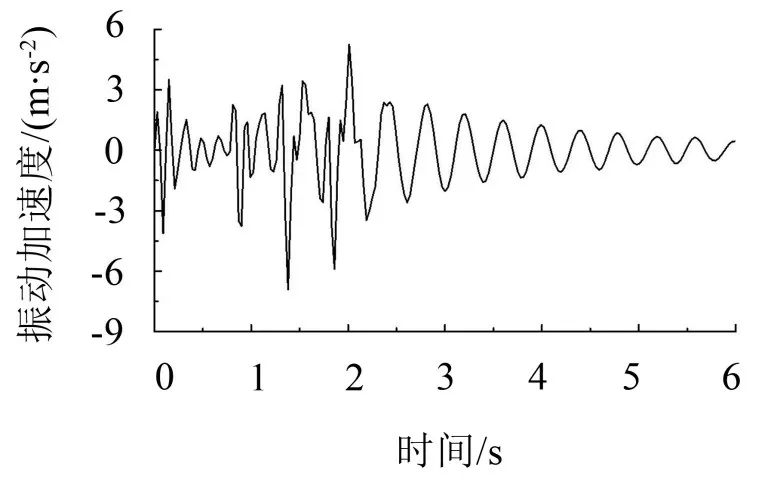
圖9 跳車

由圖5 可知，當MTVV 小于0.315 m/s2時，基本不影響駕駛舒適性，當其值大于1.15 m/s2時，將出現較為明顯的不舒適感。

由圖8 至圖9 可知，正常行駛中，車體豎向加速度為振幅0.2 m/s2的周期振動，發生跳車時，車體振動較為明顯，時程曲線的峰值位置剛好為4 個車輪的過障礙物的時刻，車輛經過橋頭后，車體開始做有阻尼的衰減振動。

表2 進一步給出了不同工況下駕駛位置處的MTVV的統計結果。

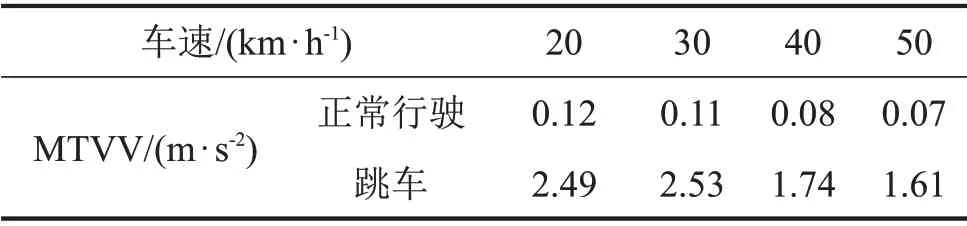
表2 駕駛位置處的MTVV

由表2可以看出：在20 km/h～50 km/h的車速區間內，正常行駛過程中，駕駛處豎向振動加速度均小于0.315 m/s2，未出現不適的駕駛體驗；跳車后駕駛位置處的MTVV 均大于1.15 m/s2，說明跳車后出現了較為明顯的不舒適的駕駛體驗。同時，不舒適體驗隨車速的增加呈現先增后減的趨勢，30 km/h速度跳車時的駕駛體驗最差，之后，隨著車速的增高，通過障礙物時間變短，車輪動量變小，從而跳車引起的振動減弱。

4.3 橋梁動力響應與峰值分析

橋梁動力響應反映了跳車沖擊過程中結構的受力性能變化規律，選用應力和位移兩個響應指標，計算跳車過程中2 個觀測點(圖3 所示)的響應時程。以20 km/h速度跳車為例，圖10、圖11分別為2個測點采用車橋分析系統及影響線靜力加載計算得到的位移和應力時程，表3 給出了不同車速下的響應峰值統計結果。

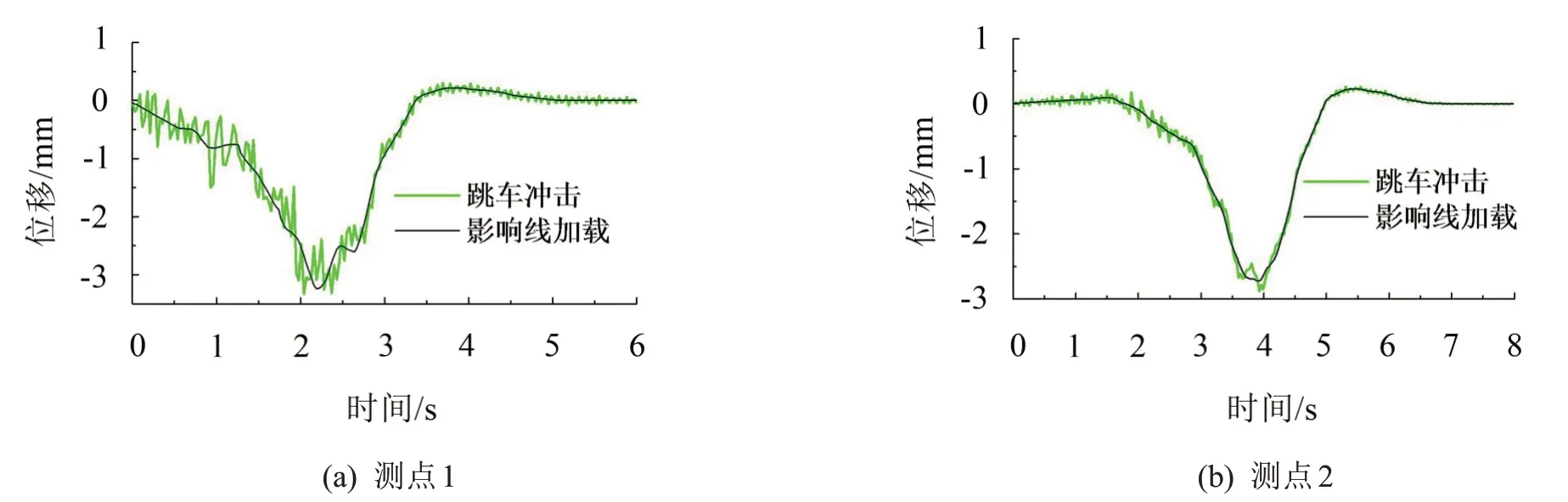
圖10 位移響應時程

圖11 應力響應時程

由圖10 至圖11 可知，相比于影響線加載，距離跳車位置較近的測點1 處的動力響應在前2 s 內變化劇烈，跳車發生后，跳車引起的沖擊效果仍然持續了將近1 s，測點2距離跳車位置較遠，位移和應力的變化幅度相對較小。表3所示

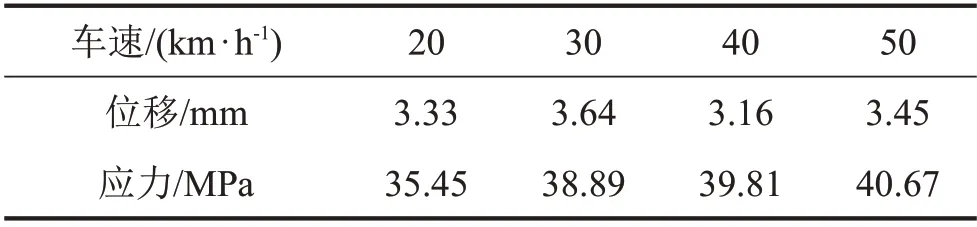
表3 4種工況下的響應峰值

由表3可知，在行車速度區間20 km/h～50 km/h內，隨車速的提高，測點處的應力響應峰值逐漸增大，位移響應峰值則呈現為先大后小再大的趨勢，計算可以發現，10 km/h 間隔內應力最大增幅為9.70 %，位移最大增幅為9.3 %，介于20 km/h～30 km/h 之間，說明30 km/h 車速下跳車會引起最為不利的橋梁位移響應。

5 結語

以21自由度的車輛模型和4跨連續鋼桁橋為對象，編制跳車過程中的車-橋耦合分析系統，為跳車導致的橋面動力荷載識別和駕駛舒適度評價等提供了有效的分析途徑，通過分析得到以下主要結論：

(1)跳車過程中車橋作用力變化劇烈，相比正常行駛，跳車瞬間車橋作用力約變化2.0 倍，車輛前后輪的接觸力相互影響；

(2)跳車引起的駕駛不舒適性體驗并非隨車速的增加而增強，而是在某一速度下跳車駕駛體驗最差，之后隨著車速的增加而有所改善；

(3)當車輛行駛速度介于20 km/h～50 km/h時，隨著車速的增大，跳車沖擊所造成的觀測點動應力水平增大，而位移響應峰值呈現先增后減的趨勢，位移響應對應的最不利車輛行駛速度為30 km/h。