幾何非線性效應對受迫振動索理論解的影響評估

梁浩博，劉小會，2，楊曙光，閔光云，伍 川

（1.重慶交通大學 土木工程學院，重慶400074；2.重慶交通大學 省部共建山區橋梁及隧道工程國家重點實驗室，重慶400074；3.國網河南省電力公司 電力科學研究院，鄭州450052)

基于經濟發展的需求，國內外很多工程領域都廣泛使用大跨度的索結構，例如橋梁工程領域的斜拉橋和懸索橋、電氣工程領域的高壓輸電線路等。然而索結構因其自身重量輕、柔度大以及低阻尼的特點，很容易在外力荷載作用下出現大幅度的振動，呈現出非常明顯的非線性現象。索的這種大幅振動極易導致整個工程結構出現損壞。因此，關于索結構的非線性動力學研究是個很重要的課題。

關于索的非線性動力學研究早在18 世紀就開展了。隨后，Routh[1]推導出懸索的運動方程并得到懸索固有頻率。Irvine 等[2]在1974年推導出水平索固有振動方程式，并對拉索的模態、頻率等參數進行系統的分析研究。文獻[3]基于哈密頓變分原理并采用Galerkin 離散法推導出單檔覆冰懸索運動方程。文獻[4]引入無量綱參數推導出受溫度變化影響的懸索面內非線性偏微分方程，利用Galerkin 法得到離散后的微分方程。文獻[5]同樣采用Galerkin法，建立一個兩自由度懸索離散模型，對懸索的1:2內共振進行了研究。文獻[6]采用Galerkin方法得到懸索的時滯微分方程，以對其主共振進行分析。

由于大跨度輸電線路實質上也屬于索結構，因此關于輸電線路的學術研究同樣可以為拉索研究帶來指導性意見。Rega等[7]引入無量綱參數并基于哈密頓變分原理推導出輸電線面內非線性偏微分方程，接著應用Galerkin 法和多尺度法求解該方程。汪峰等[8]基于Galerkin 模態截斷法和多尺度法推導出斜拉索面內振動方程并得到幅頻響應方程，分析了梯度溫度場等因素對振動的影響。文獻[9]基于懸鏈法和熱應力理論推導出考慮溫度效應的覆冰導線偏微分方程，接著采用Galerkin 法和多尺度法將其離散和求解。受限于非線性理論的發展，上述眾多學者關于理論方程的求解都是基于模態疊加法對系統進行了線性化處理，最終得到結構的近似分析解。該處理方法雖然在一定程度上簡化了計算，但對于這些具有幾何非線性的結構是否可以直接使用，會不會對結果造成誤差等等，這些問題仍有待商榷。

國內學者趙躍宇等[10]以懸索為例，并引入新的無量綱參數得到無量綱懸索面內運動方程，對結構非線性動力學中常用的Galerkin法和直接法進行了對比，發現離散法并不適用于所有結構非線性動力學的求解。文獻[11]中，作者采用小參數法得到久期項導致的懸索振動形態，并與Galerkin 離散法得到的相應振動形態進行對比，最終驗證了小參數法的可行性。然而上述文章均是以兩種算法的對比為主要目的，針對Galerkin 離散法本身的適用性并未作出詳細區分。

另外，Rega 等[7]和趙躍宇等[10]分別引入了不同的無量綱參數將運動方程無量綱化，但卻并未有學者對這兩種無量綱參數對系統非線性的影響以及兩種無量綱方法是否適用于所有結構非線性系統做詳細的研究。

因此，本文基于簡單的單跨拉索力學模型以及振動理論，針對Galerkin 離散法和兩種無量綱方法的適用性進行詳細討論。

1 基于Galerkin方法的水平拉索受迫振動數值解

1.1 力學模型及兩種無量綱方法

設單跨拉索兩端處于同一水平高度，在自重作用下位于如圖1所示的XOY平面內，X軸沿拉索弦向方向，Y軸沿拉索豎向垂度方向。拉索跨徑為l，其變形可以分為兩部分：

圖1 單跨水平拉索力學模型

(1) 拉索在自重作用下處于靜平衡狀態，垂度為d；

(2)拉索在面內外部荷載作用下產生處于XOY平面內的位移。

考慮到拉索在受到幾何非線性和三向耦合時所引發的動力學問題很復雜，本文將模型簡化，做出如下假定：

(2)本構關系符合胡克定律；

(3) 不考慮彎曲、扭轉以及剪切，忽略其軸向運動；

(4)不考慮張力沿拉索軸向的變化。

圖1所示理論模型中，考慮沿拉索Y向施加均布簡諧激勵荷載Pcos(Ωt)，P為激勵幅值，Ω為簡諧激勵的頻率。取圖1中拉索處于靜平衡狀態下的微段ds進行研究，可以得到單跨拉索的面內運動方程：

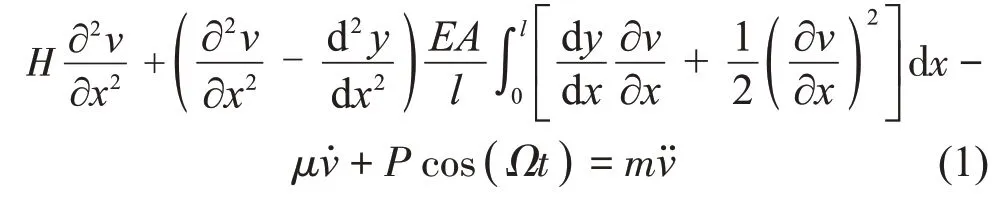
式中：H為拉索在自重作用下達到靜平衡狀態時的水平張力，v為沿拉索面內Y向的位移，E為拉索彈性模量，A為拉索橫截面積，m為拉索單位長度質量，μ為黏性阻尼系數。

引入無量綱參數：

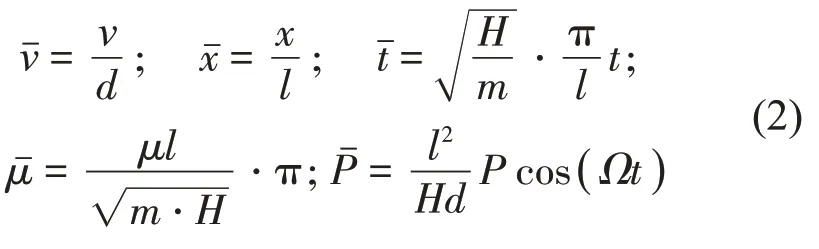
將上述參數代入式(1)，得到拉索面內無量綱運動方程：

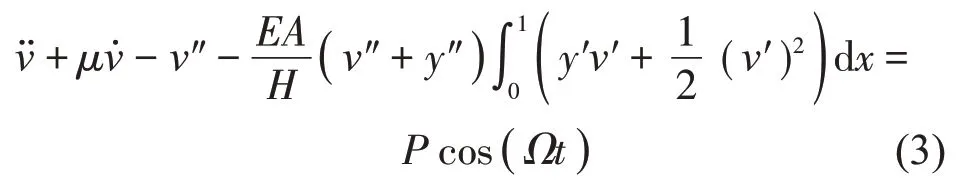
為了方便后文書寫，式(3)中各無量綱參數的上劃線“-”均已省略（后文同）。式(3)中“v′”表示對無量綱時間t求1 階導，“v″”表示對無量綱位移x求2階導。

由于v是關于時間t和位移x的參數，根據Galerkin理論，可將其分離變量為：

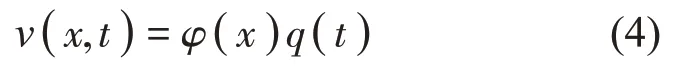
其中：φ(x)為模態函數，q(t)為時間函數。

將式(4)代入式(3)中，并在方程兩端乘以模態函數φ(x)，接著在x∈[0，1]內進行積分，可得到：

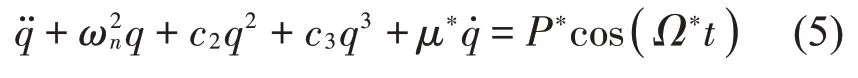
式中：

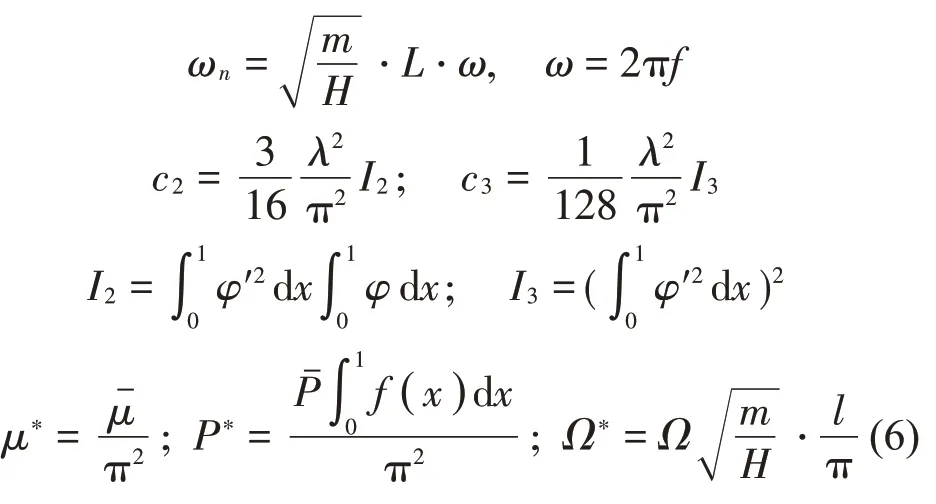
其中：λ2為Irvine 參數，見式(7)。該參數可以反映拉索的垂度效應。λ的值越大，拉索的垂度越大。ωn即為無量綱化后的頻率，ω表示面內自振等效圓頻率，f為拉索自振頻率。式(5)中q上方的點“˙”和“˙˙”，分別表示對無量綱時間t求1階導和2階導。

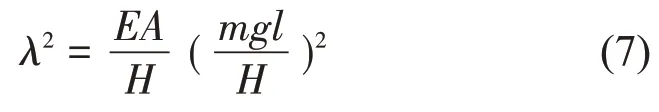
g是重力加速度。

引入另一種無量綱參數：

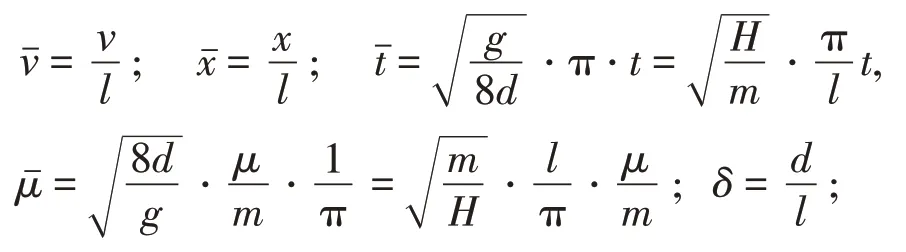
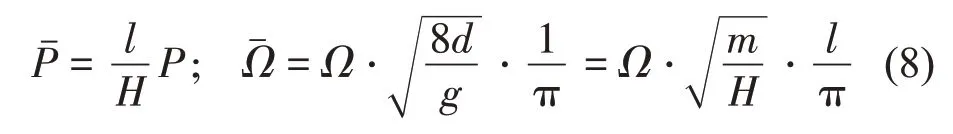
式中：δ為垂跨比，張力H可表示為：

取其無量綱靜態垂度曲線為：

將上述無量綱參數代入式(1)，可得拉索面內無量綱運動方程：

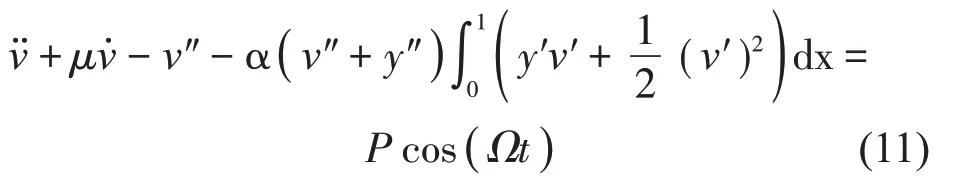
式中：

同樣，該式通過模態疊加法可得到：

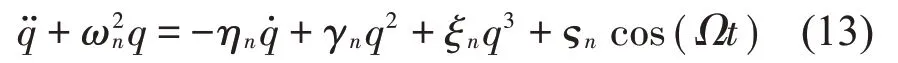
式中：

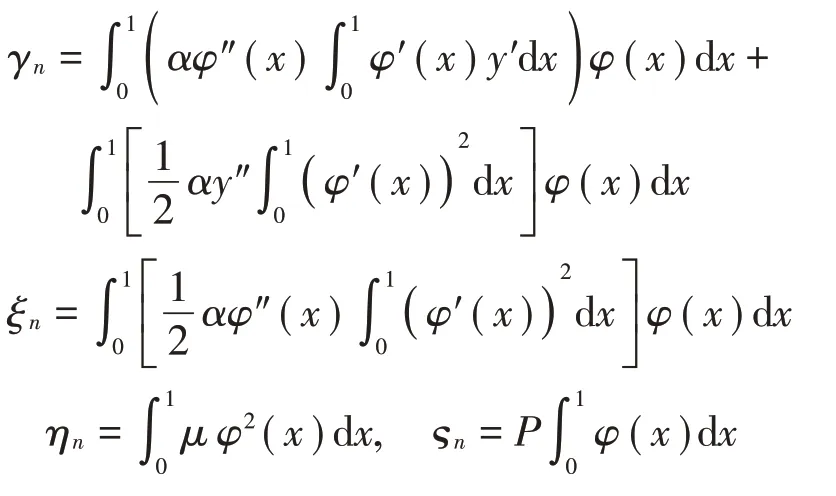
由于兩種無量綱方法主要區別在于豎向位移v所除是d還是l，故下文均以無量綱d″和無量綱l″來分別表示兩種不同的無量綱方法。

1.2 單跨水平拉索面內頻率及模態

研究拉索在外激勵作用下產生受迫振動的現象，首先要研究其頻率和對應模態。其中模態分為兩種形式，對稱模態與反對稱模態。本文主要研究對稱模態。

取方程(3)的線性部分（忽略阻尼項）及邊界條件：

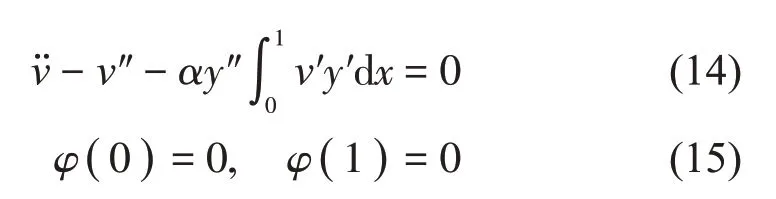
令v=φ(x)eiωt并將其代入式(15)中，結合邊界條件可得拉索面內模態函數：

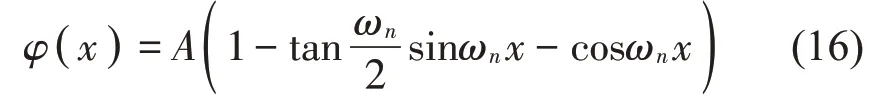
取正交模態：

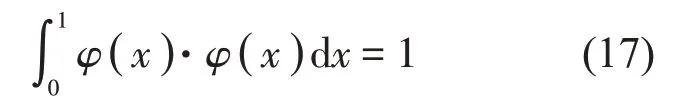
ωn可由超越方程式(19)求得：

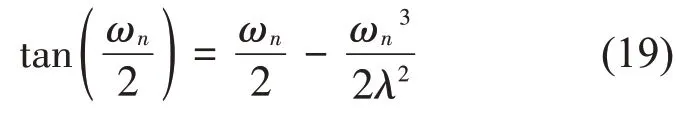
1.3 兩種無量綱方法的數值解對比

觀察式(1)的拉索面內運動方程發現，方程的形式較為復雜，且變量較多，不利于進行數值求解。而引入無量綱參數就可以減少變量數目，便于后續求解。同時，由于對參數進行了無量綱化，更方便做不同工況下的參數對比。

但是可以注意到兩種方法關于面內豎向位移v的處理方法是不同的，這是否會導致兩種方法所得結果出現一定的差異，本文考慮將這兩種方法做對比（拉索物理參數均取自文獻[12]，詳見表1）。

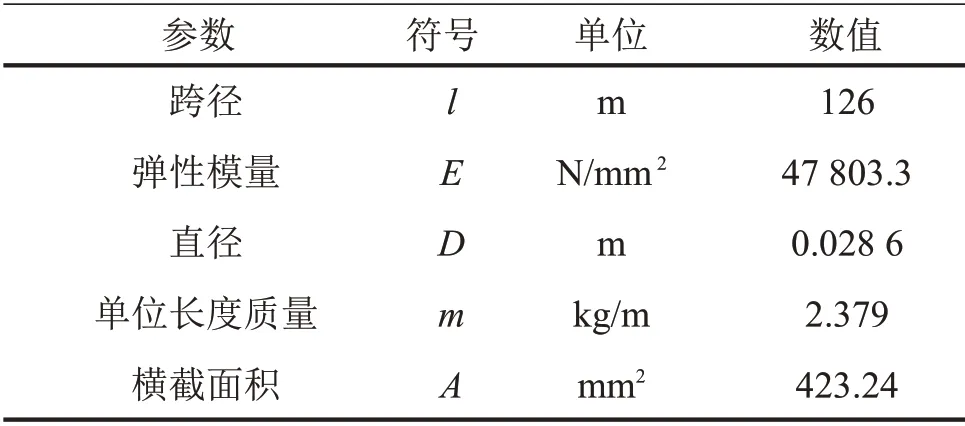
表1 拉索物理參數

文中系統的黏性阻尼系數μ均采用瑞利阻尼，具體計算方法如下：

取α為0.02，β為0，將其代入公式中，即可得到阻尼比ξ。而阻尼μ則可由公式μ=2ξωm得到。

由式(7)可知：受到張力和垂度的影響，不同參數對應的拉索非線性強度各不相同，故本文選取λ為等于1π、3π、7π、9π等4種工況進行研究。4種工況下的具體參數見表2。

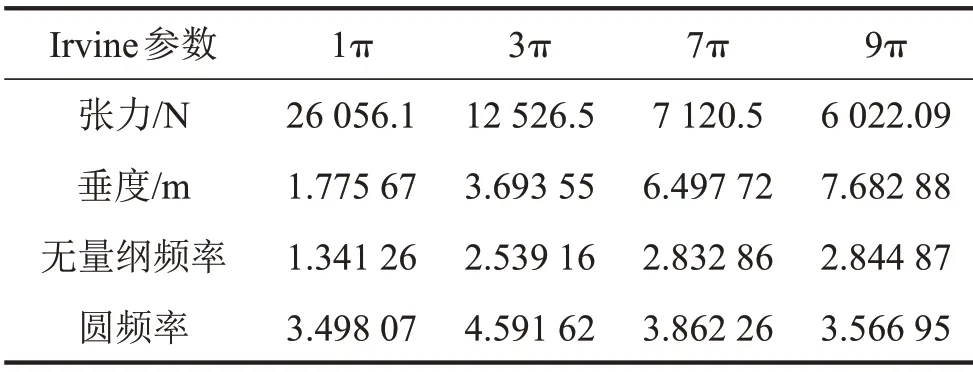
表2 不同Irvine參數對應的物理參數

將表1 和表2 具體參數導入MATLAB 程序中，即可運行得到系統時間歷程曲線，如圖2所示。

2018年1—8月，全國國有及國有控股企業（本月報所稱全國國有及國有控股企業，包括中央管理企業、中央部門和單位所屬企業以及36個省、自治區、直轄市、計劃單列市的地方國有及國有控股企業，不含國有金融類企業。以下簡稱國有企業）經濟運行態勢良好。償債能力和盈利能力比上年同期均有所提升，利潤增幅高于收入10.4個百分點，鋼鐵等行業利潤增幅較高。

通過觀察圖2可知：無量綱d方法相較于無量綱l方法所得幅值略大，尤其在λ=1π 時，差距較為明顯，但隨著λ值的增大，這種差距逐漸縮小，直至忽略不計；同時由表3可知：兩種無量綱方法均會使系統非線性系數增大，尤其以無量綱l方法增加最大。

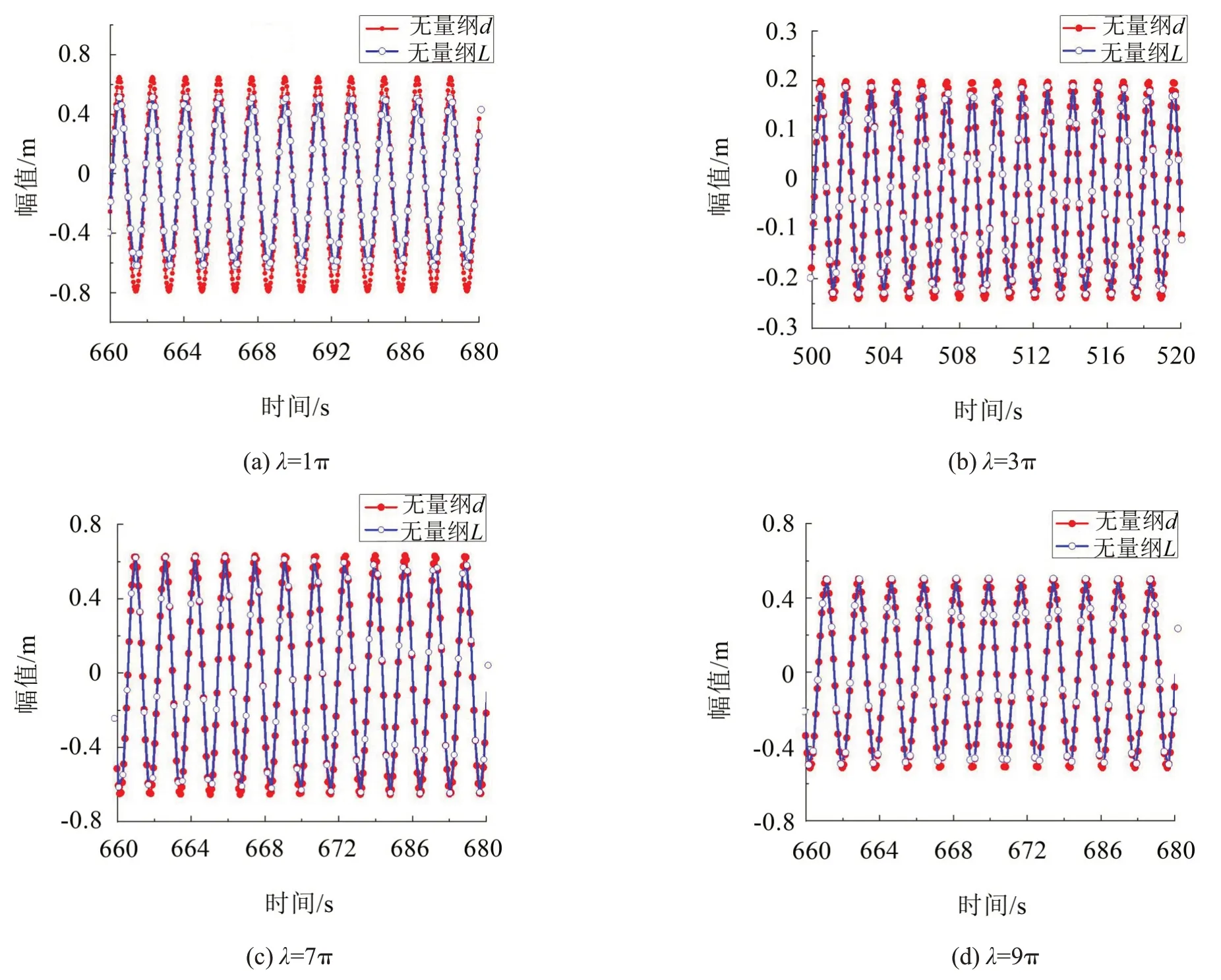
圖2 兩種無量綱方法時間歷程曲線

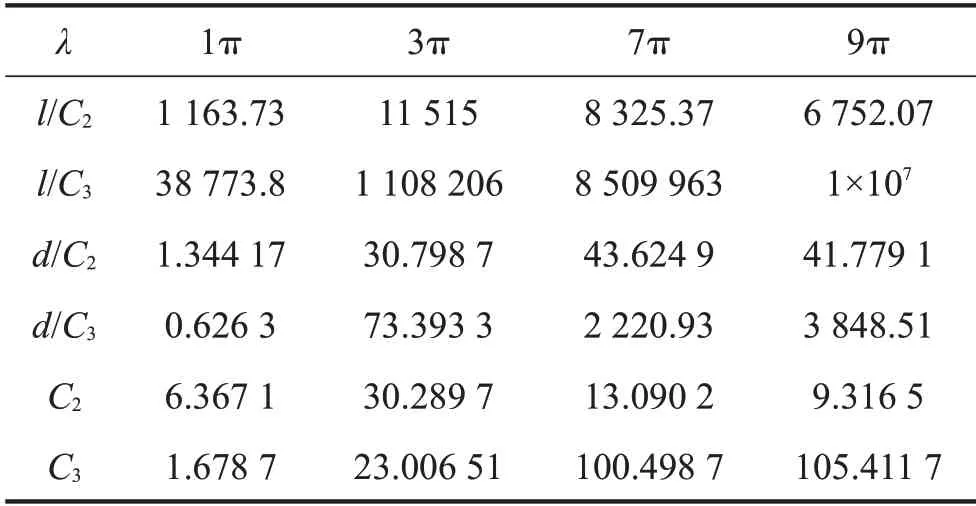
表3 不同Irvine參數對應的非線性項

2 基于多尺度法的受迫振動理論解

由于拉索運動方程比較復雜，一般難以求得其精確解，且拉索振動屬于弱非線性問題，因此可采取近似的解析方法求解。傳統的解析方法主要包括：漸進法、多尺度法、平均法等，而多尺度法是其中應用得最廣泛的方法。本文亦采用多尺度法來分析系統響應。

為了滿足多尺度法的求解條件，首先對式(1)直接采用模態疊加法進行離散。接著，為了使非線性項，外部激勵和阻尼出現在同階中，引入無量綱小量ε，經過化簡后，式(1)即可轉化為：

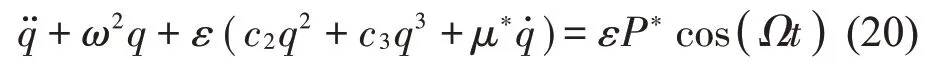
式中：

上式(21)中的等效圓頻率、平方和立方非線性項系數以及外激勵中所包含的I的取值可表示為：

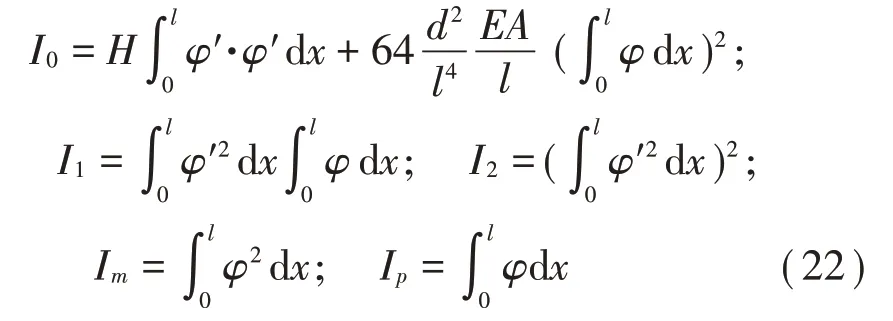
為了方便書寫，后文已將式(20)和式(21)中的“*”忽略。

引入以下參數：

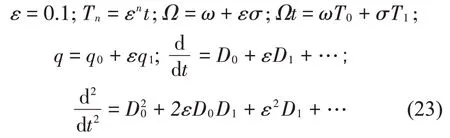
其中：σ為調諧參數。

將式(23)代入式(20)中，并比較ε同次冪項的系數，可得：

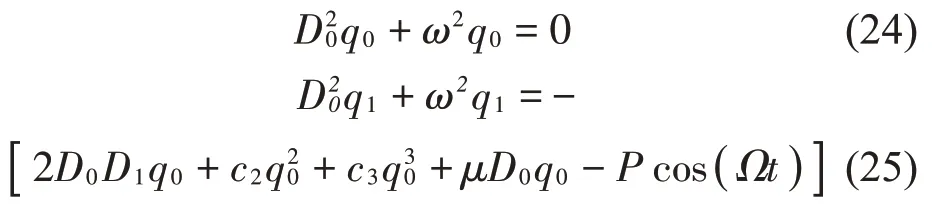
式(24)的解可用指數形式表示為：

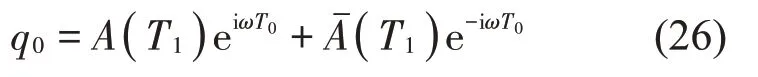
此時，A可寫成極坐標形式：

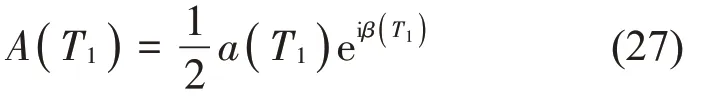
式中：a表示振幅，β表示相位。

將其代入式(25)中，即可得到：

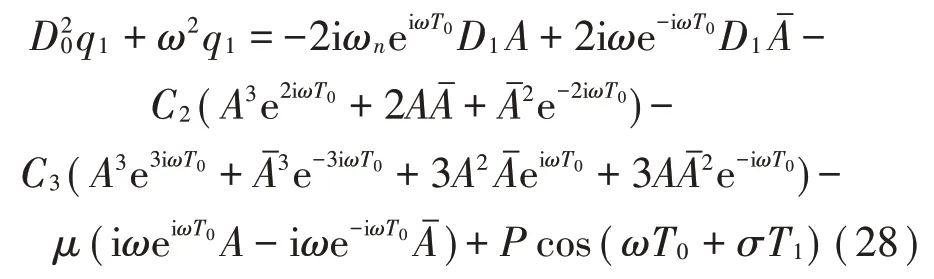
消除式(28)中的久期項，可得：

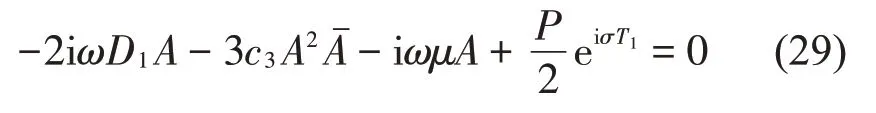
將上式進行化簡可得：

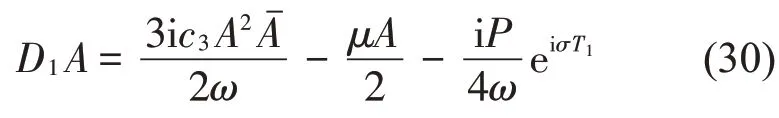
并將A代入式(30)可得到：

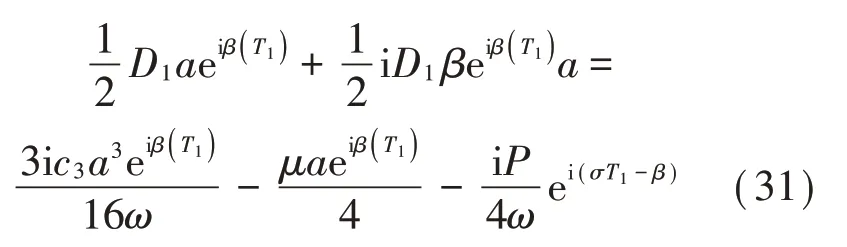
分離實部和虛部可得：

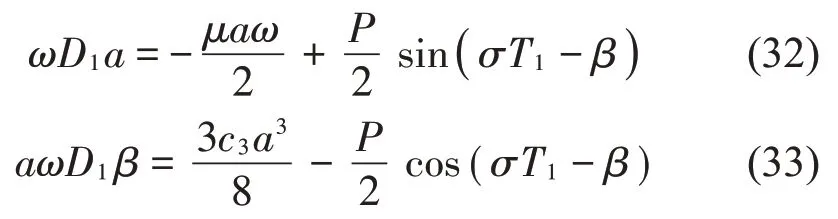
引入：

方程即可轉化為：

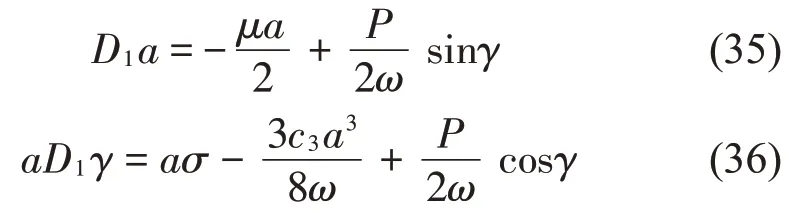
令D1a=0，D1γ=0可得出以下方程：

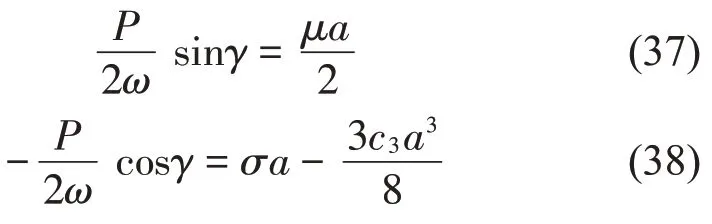
上述方程兩端各自平方并相加即可得幅頻響應方程：

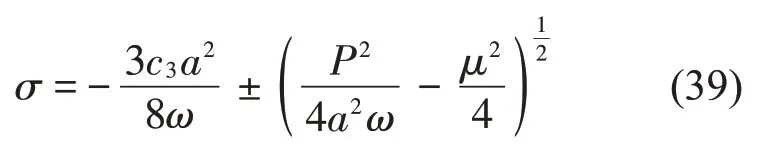
由式(39)并結合表1中的拉索物理參數，即可得出拉索的幅頻響應曲線，見圖3。

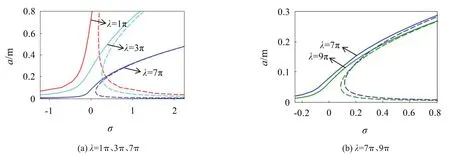
圖3 幅頻響應曲線

如圖3 所示：橫坐標σ表示調諧參數（無量綱），縱坐標a表示幅值（單位為m）。實線表示穩定值，虛線表示不穩定值。

結合曲線和式(23)所引入的小量可知：當調諧參數σ=0時，外激勵頻率與系統固有圓頻率相等，此時拉索產生主共振。同時，隨著λ增大，系統非線性不斷增強，曲線出現跳躍現象，幅值也出現明顯的衰減。

當σ=0時，將參數代入式(39)中可得到系統穩定后的理論幅值為：(1π)0.589 27 m；(3π)0.210 062 m；(7π)0.062 395 m；(9π)0.051 052 m。

將該理論幅值與1.3 節中兩種無量綱方法穩定后的幅值對比后發現：無量綱d方法與理論解的誤差依次為：22 %(1π)，3.797 %(3π)、2.124 %(7π)、0.878%(9π)；無量綱l方法與理論解的誤差依次為:4.323 %(1π)、3.688 %(3π)、2.624 %(7π)、3.005 %(9π)，總體來看無量綱l方法所得結果更接近理論解。

3 不同方法結果的對比

3.1 單跨水平拉索有限元模型

由于拉索在受到覆冰、外部激勵等因素的影響時，易產生較大的振動幅度。因此不易通過實驗來獲取數據，以驗證理論，而這時采用有限元方法數值模擬拉索的振動便成為了研究拉索受迫振動的重要手段[13-14]。

然而在實際工程中，拉索振動時具有明顯的幾何非線性效應，通過有限元模擬所得的結果是否會考慮到這種非線性效應的影響?是否會產生誤差?因此，本文通過建立有限元模型，來模擬拉索的受迫振動，并將結果與數值解作對比。

采用桿單元模擬單跨拉索，網格數量為100。由于本文僅討論研究拉索在垂直方向上的運動，故在拉索兩端施加邊界條件，將其完全固定。

采用參數化建模后，第一步：在拉索上施加重力荷載，以對其進行非線性靜力變形分析。第二步：頻率分析，提取拉索的前30 階固有頻率及模態，并與基于理論所得的固有頻率作對比,見表4。第三步，沿拉索豎向施加均勻外力激勵，以使其產生面內的豎向振動，力的大小設置為0.7 N(相當于施加大小為5.6 m/s風速的風荷載)。阻尼項選取瑞利阻尼。

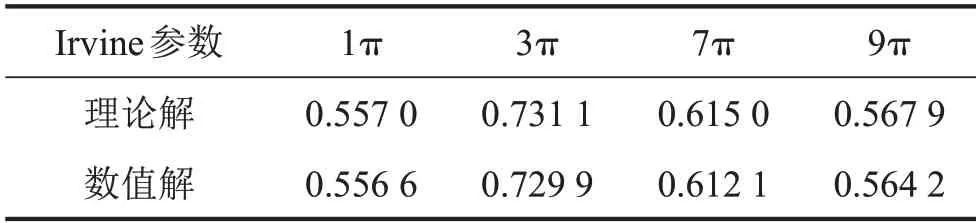
表4 不同垂度下拉索第一階面內對稱模態自振頻率對比

3.2 共振時的數值解與理論解對比

重點考慮最危險的情形，即拉索產生主共振。將表1和表2的拉索物理參數分別輸入ABAQUS軟件和MATLAB程序中，即可運行得到系統時間歷程曲線。由第2節在本文方法基礎上分別使用兩種無量綱參數所得數值解與理論解相比的誤差可知：無量綱l方法所得結果與理論解吻合良好。限于篇幅，本文僅給出使用無量綱l方法時本文方法所得數值解與有限元解的對比結果，如圖4至圖7所示。

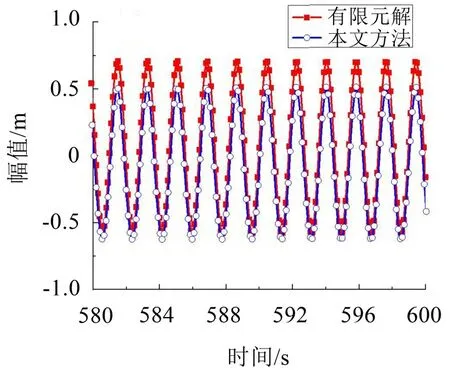
圖4 (λ=1π)拉索面內對稱模態共振時間歷程曲線

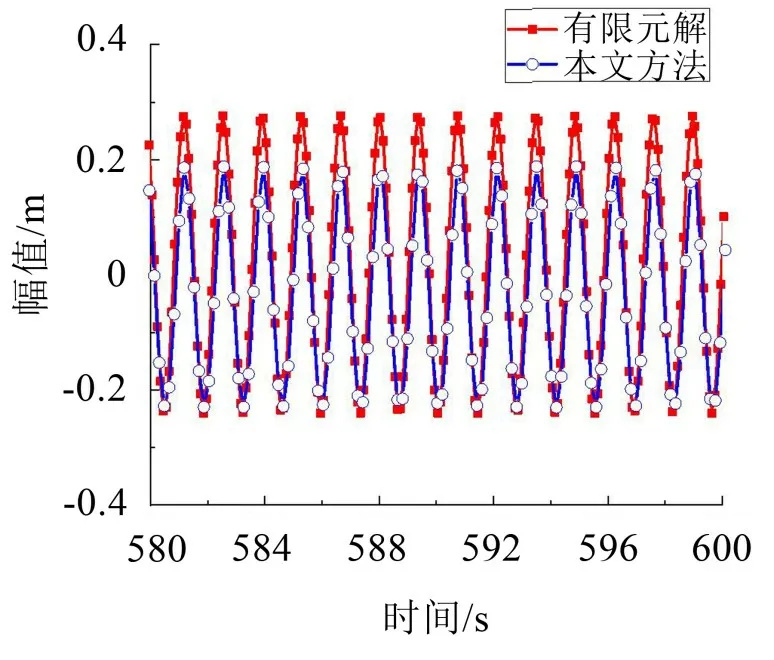
圖5 (λ=3π)拉索面內對稱模態共振時間歷程曲線

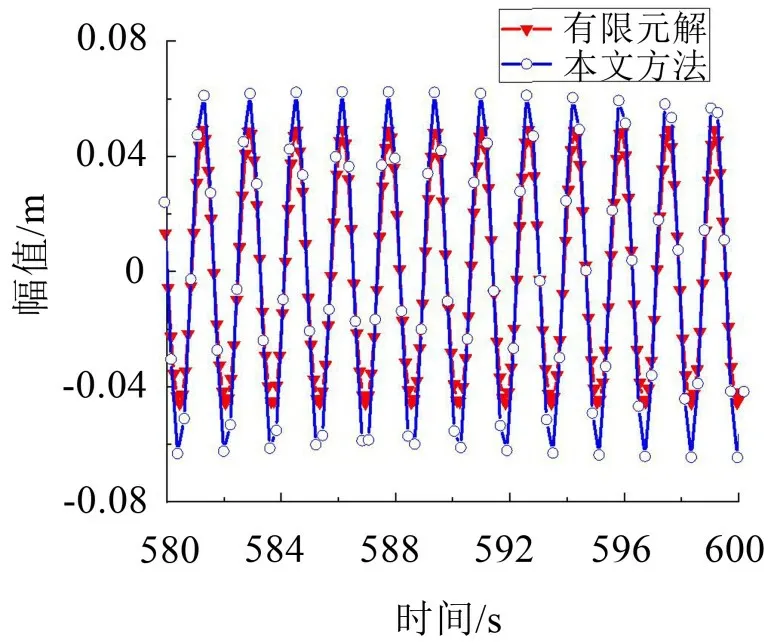
圖6 (λ=7π)拉索面內對稱模態共振時間歷程曲線

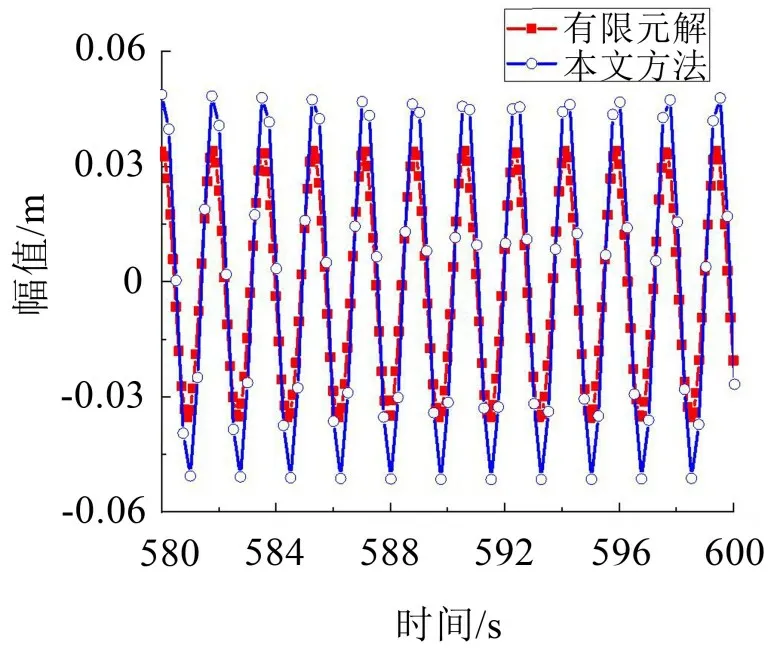
圖7 (λ=9π)拉索面內對稱模態共振時間歷程曲線

如圖4、圖5所示：當λ取1π、3π時，有限元解出現往幅值為0的水平線上方偏移的現象，而本文方法的計算結果則出現向下偏離的現象（偏移量見表5）。造成該現象的主要原因是由于系統中平方非線性項的存在，如：式(5)中的c2、式(13)中的γn以及式(20)中的εc2項，具體數值見表3；該項越大，偏上或偏下的程度也就越大。同時，由于λ取1π、3π 時系統的振動幅值較大，其偏移也就相對更加明顯。當λ=7π和9π時，由于本身幅值很小，加之平方非線性項在7π 和9π 時逐步減小，故其偏移程度也相對很小。

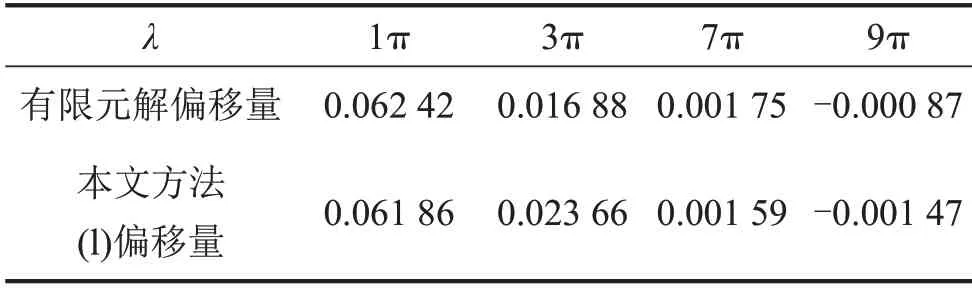
表5 共振時拉索的時間歷程曲線偏移量

如圖4至圖7所示并結合表6、表7可以發現：本文方法所得數值解與上節幅頻響應函數計算得出的理論解吻合良好，而有限元解與本文方法所得數值解相比則出現了不同程度的幅值差距。這種差距呈現出隨著λ增大而增大的趨勢。

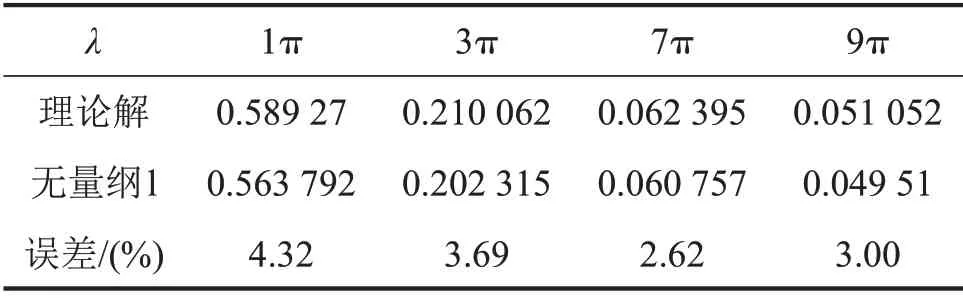
表6 無量綱l方法所得數值解與理論解對比

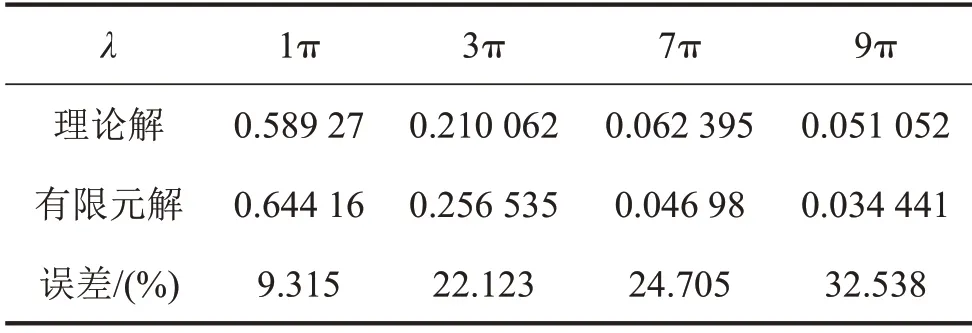
表7 有限元解與理論解對比

如圖6、圖7 所示：本文方法所得數值解較之有限元解更大，其原因在于當使用有限元軟件進行模擬時，能夠真實的體現非線性動力響應，而本文方法得到的數值解是采用了Galerkin離散法近似化的運動方程，這種近似化的方法弱化了非線性。綜合上述系統非線性越強，幅值就越小的結論，最終出現了圖6、圖7所示結果。

3.3 非共振時的幅值比較

就實際情況而言，拉索因發生共振而造成破壞的情況極少，大多是在覆冰和風載兩種主要影響因素下所造成的非共振區的大幅度振動。因此本節通過將施加在拉索上的外激勵頻率（ω=4 rad/s）偏離其固有圓頻率并采取與上一節相同的模式來進行對比。其中，λ=1π、3π、7π、9π 時頻率偏離大小分別為：0.501 9 rad/s、-0.591 6 rad/s、0.137 7 rad/s、0.433 0 rad/s（外激勵頻率減去固有圓頻率）。

如圖9 至圖12 所示：其部分現象與共振區現象一致。而圖9所示結果出現了有限元解與本文方法所得數值解差距較大的現象。初步結合表2 判斷，造成該現象的原因是所施加的外荷載激勵頻率小于λ=3π時的固有圓頻率（ω=4.59 rad/s）。為驗證該判斷，本文取ω=4.8 rad/s 時，采用無量綱l方法進行再次對比，結果如圖12所示，表明判斷正確。

圖8 (λ=1π)拉索面內對稱模態非共振時間歷程曲線

圖9 (λ=3π)拉索面內對稱模態非共振時間歷程曲線

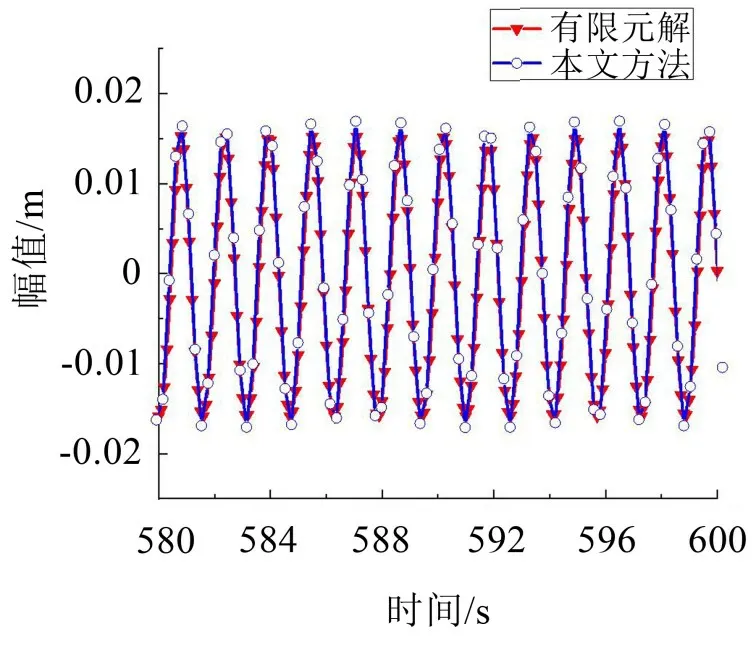
圖10 (λ=7π)拉索面內對稱模態非共振時間歷程曲線

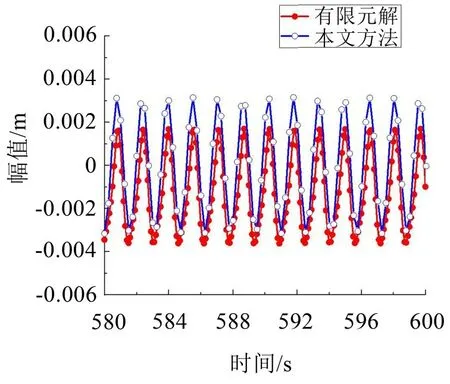
圖11 (λ=9π)拉索面內對稱模態非共振時間歷程曲線

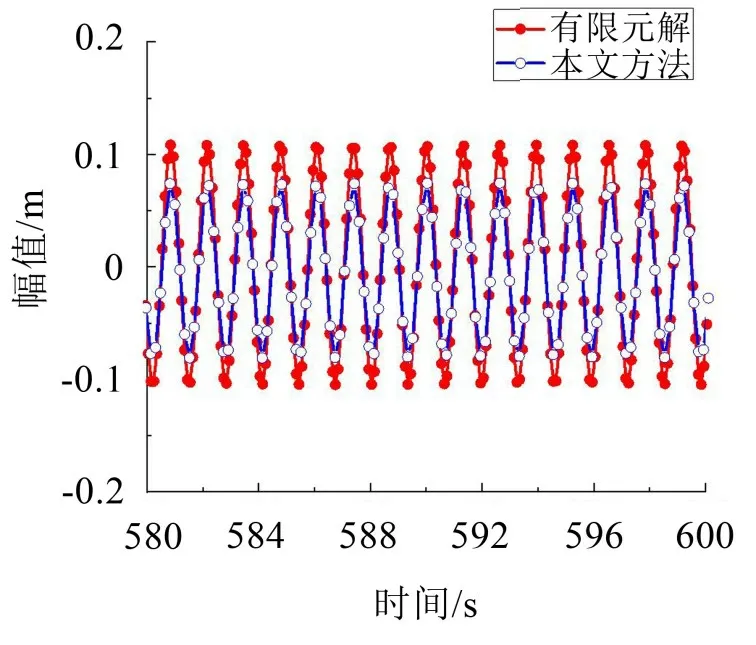
圖12 (λ=3π)拉索面內對稱模態非共振(ω=4.8 rad/s)時間歷程曲線

由圖（12）可以發現：當所施加外部激勵頻率為4 rad/s 時，圖中所呈現出的現象并無明顯規律。分析可知：在非共振區，本文方法所得數值解與有限元解的差距，主要取決于外激勵頻率的大小與其圓頻率的差距。外激勵頻率與圓頻率的差距越大，本文方法所得數值解與有限元解的差距也就越大。同時，隨著λ值的變大，其時間歷程曲線就相對不規則，甚至出現相位差，如圖11所示。

4 結語

本文通過應用Galerkin離散法得出拉索無量綱面內振動方程，并運用多尺度法得到系統的幅頻響應曲線，最后分別通過ABAQUS 和MATLAB 進行了4 種工況的數值模擬和有限元分析對比，主要得出以下結論：

（1）隨著系統非線性的增強，幅值逐漸減小，而有限元解與理論解的差距則逐漸增大，說明Galerkin離散法對于弱非線性系統適用性更高，系統非線性越強，誤差就越大。

（2）系統的平方非線性項會造成有限元解和本文方法所得結果分別產生向上和向下的偏移。

（3）隨著λ值的增大，兩種無量綱方法差距微小，總體而言經過無量綱l方法得到的運動方程所得的系統時間歷程曲線更接近理論解；為了使結果更精確，當系統非線性強時可采用無量綱d方法，系統非線性弱時則采用無量綱l方法較好。