從一道八省聯考題談函數切線問題的求解
江蘇省興化市楚水實驗學校 (225700) 袁小強
1.引例
(1)人教版《數學選擇性必修第二冊》第99頁習題5.3第12題:利用函數單調性證明下列不等式,并通過函數圖象直觀驗證:ex>1+x,x≠0.
本題要求通過函數圖象直觀驗證,如圖1,從函數圖象上看,y=ex圖象恒在y=x+1的上方,從而ex≥x+1,并且發現這兩個函數相切于點(0,1)處,但是從不等式證明角度來看,嚴格的邏輯證明只能是從定義、定理公式、法則等出發,不能通過圖象作為證明依據,于是通過構造函數h(x)=ex-x-1,利用研究導數單調性求出函數最值,從而解決問題,由h′(x)=ex-1,當x<1時,h′(x)<0,h(x)單調遞減;當x>1時,h′(x)>0,h(x)單調遞增.因此h(x)≥h(x)min=h(0)=0,因此不等式得證.

圖1
(2)人教版《數學選擇性必修第二冊》第97頁練習第1題:利用函數單調性證明下列不等式,并通過函數圖象直觀驗證:sinx 顯然該式可以推廣到一般情況:sinx 圖2 例1 (2021八省模考22題)已知函數f(x)=ex-sinx-cosx,g(x)=ex+sinx+cosx. (2)若g(x)≥2+ax,求a. 圖3 (2)由g(0)=2發現函數g(x)過(0,2),而y=2+ax也過(0,2),兩個函數有公共點,如圖4,從圖象上聯想到可能是切線,也就是函數g(x)=ex+sinx+cosx在(0,2)處的切線就是y=ax+2,從而通過函數導數性質及零點存在性定理“小心求證”,從而掌握研究導數問題的一般方法:從“直觀感知”到“推理論證”. 圖4 2°、當x≥0時,令y=x+1-sinx-cosx≥x-sinx,令φ(x)=x-sinx,則φ′(x)=1-cosx≥0,從而φ(x)在(0,+∞)單調增,φ(x)≥φ(0)=0,于是x+1≥sinx-cosx; (2)令G(x)=ex+sinx+cosx-2-ax,則G(0)=0. 1°、當a=2時,G(x)=ex+sinx+cosx-2-2x,則G′(x)=ex+cosx-sinx-2,G″(x)=ex-sinx-cosx≥0,于是G′(x)單調增,又G′(0)=0,從而G(x)在(-∞,0)單調減,在(0,+∞)單調增,G(x)≥G(0)=0成立,因此a=2; 綜上a=2. 變式1 (2020泉州模考題)已知函數f(x)=sinx,g(x)=2x2-1. 圖5 解析:(1)F(x)的單調增區間為(0,+∞),單調減區間為(-∞,0)(過程略). 綜上,a≥-1. 1°、當a=0時,不等式恒成立,因此a=0; 曲線的公切線問題一直是高考的熱點,其中涉及證明、求值或求范圍問題.此類問題研究對象在變,但思想方法不變,研究套路不變,精準地把握函數導數問題的切入點“切線”,才是解決導數問題的“王道”.研究兩個函數(直線與曲線、曲線與曲線)之間的關系,借助切線(或公切線)這個紐帶和橋梁,從而巧妙地轉化為直線與曲線的關系,并用嚴格邏輯推理證明“猜想”.此類問題解題方向明確:一般是先找切線,再導數證明.導數搭臺,切線唱戲,多題歸一,從直觀感知到推理論證,這樣培養了學生的科學精神和創新意識,能引導學生感悟數學的科學價值、應用價值、審美價值,從而實現數學解題的育人價值.
2.聯考題及解答



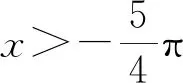





3.變式










4.結語

