挖掘函數中隱含的性質巧解題

浙江省寧波市奉化區溪口中學 (315501) 金 杰

在一些函數問題中，雖然給出了函數表達式，但由于表達式比較復雜，不能直接通過函數式的代入解決問題，而需要對函數式進行代數變形，挖掘出函數的性質，再運用函數性質來解題，本文舉例介紹幾個常見模式，供讀者朋友參考.

一、挖掘函數的單調性

點評：本題是一個解函數不等式問題，由于給出的函數表達式比較復雜，所以通過直接表示出f(x+a)和f(2a-x)后解不等式是不可能實現的，找到函數的單調性才是解決問題的關鍵.

(i)當a>0時，函數f(x)的圖象如圖1所示，從而，f(x)在(-∞,+∞)上單調遞增，故由a>0?x+a>x?f(x+a)>f(x)，故不符合題意.

圖1 圖2

點評：本題通過對參數a進行分段討論，化解了問題的難點，同時也顯示此時有針對性的畫圖更能清晰地反映函數的性質，找到問題的實質.

二、挖掘函數的奇偶性

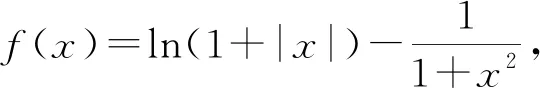
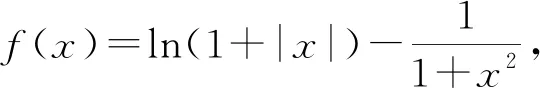
點評：本題的解決是從探求給出函數的單調性、奇偶性入手，將一個隱含關系變成一個簡單的不等式，避免了分類討論和復雜的代數運算.

點評：通過對已給的函數化簡分析，再構造了一個奇函數，這樣問題轉化為可利用奇函數性質解決的問題.由于最值是相對復雜的問題，具體問題具體分析，抓住特點，順勢而為.

三、挖掘函數的周期性

解析：考察所給的分段函數，當x>0時是一個周期函數，由于方程f(x)=x+a有且僅有兩個不相等的實數根，分別畫出函數y=f(x)和y=x+a如圖3，可看出實數a的取值范圍是[3,4).

圖3

點評：利用函數圖象可直觀地得到一些參數范圍問題，但對畫函數圖象的要求比較高，特別需弄清楚函數的性質及基本走向、經過的特殊點及循環往復的周期情況等.

例6 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,0≤φ≤π)一個周期圖像的最高點是(2,2)，與它相鄰的最低點的橫坐標是6，求f(1)+f(2)+f(3)+…+f(2020)的值.

點評：欲求一些函數式若干項的和的問題，找出其式子規律性(如周期性)是非常重要的思維走向，解題時有如此的意識就能抓住機會，機智破題.

四、挖掘函數的對稱性

解析：由于y=f(x)+f(2-x)是關于x=1對稱，所以只要了解函數在[1，+∞)上的變化情況就能解決問題.由于f(x)+f(2-x)=

圖4

點評：通過利用函數的對稱性，求出函數解析式并畫出函數圖像，再由數形結合分析題意，轉化求解，就使問題獲得了圓滿的解決，此處分段去絕對值符號很重要.

點評：由于x與2a-x關于x=a對稱，所以f(x)與f(2a-x)在同一個單調區間內，抓住這個特殊條件將兩個函數式配湊在一起是一個很好的選擇.