關于圖形旋轉變換專題的解題方法探究

吳艷華

(江蘇省蘇州工業園區星瀾學校 215000)

《數學課程標準》提出了數學教學總體目標，其中包括了學生對于數學圖形旋轉變換的認知，并要求學生掌握幾何圖形的基礎知識.對于初中數學課堂上的圖形旋轉變換題，教師應幫助學生探索線段、平行四邊形、多邊形等基本圖形的相互特征.通過變換演示了解圖形的前后對應關系.知曉圖形變換題的一般化解決步驟，讓學生不再畏懼圖形的旋轉變換題目.

一、判斷圖形的具體形狀

例1已知圖1的四邊形ABCD是正方形，三角形ADE通過順時針旋轉與三角形ABF重合.

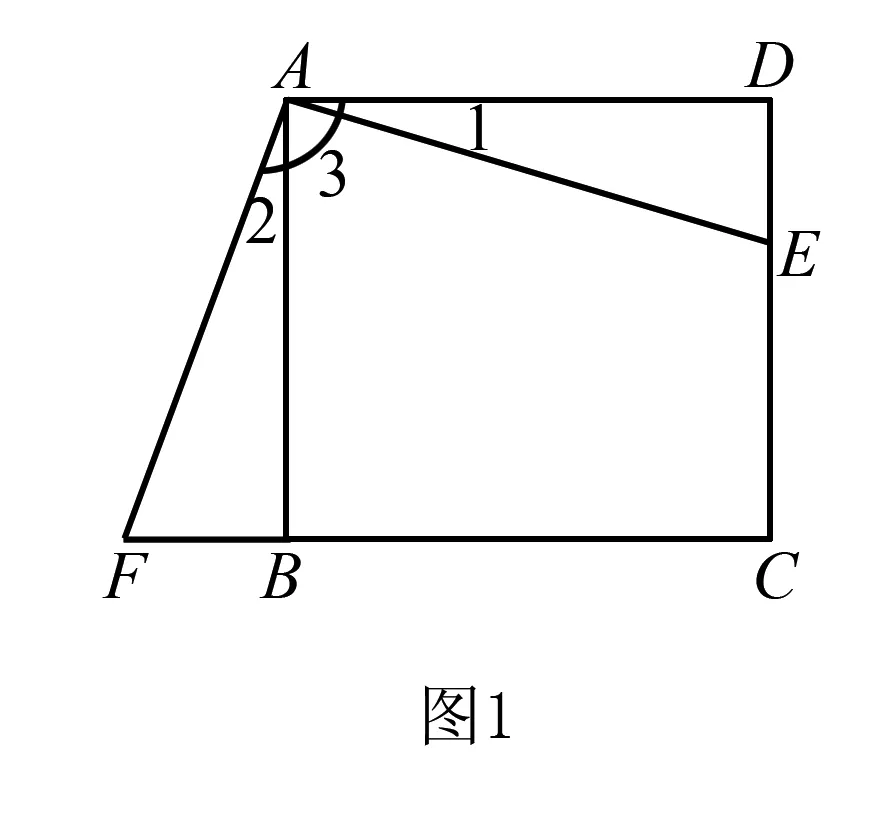
(1)旋轉中心位于哪里？

(2)圖形總共旋轉了多少度？

(3)如果連接了EF，那么三角形AEF是什么三角形呢？

對于該道題目的解答，教師應著重幫助學生領會到旋轉變換的具體概念以及其變換后的基本性質.學生能夠通過觀察直接寫出第一問和第二問的答案，但是對于第三問，一些學生在進行解題時卻遇到了一些麻煩.此時教師就應該組織學生進行合作探討，幫助學生回顧之前所學習過的知識.了解三角形的形狀有直角三角形、等腰三角形、等邊三角形，之后再由旋轉和它所旋轉的圖形得知對應點到旋轉中心的距離相等.而兩組對應點還分別與旋轉中心連線所對應的兩個角相等，由此學生也會很容易的去連接線段EF.并利用好AE=AF，得出∠FAC+∠1=∠2=90°，由此去判斷出三角形AEF就是等腰直角三角形.在解答這一類的數學問題時，教師應由圖形的旋轉變換關系進行入手.鼓勵學生在分析過程中了解旋轉變換過后的變與不變關系，讓學生分清圖形的基本形狀，了解旋轉的必要特征.在此基礎之上，教師還要對基本題目進行適當拓展.幫助學生理解不同變換模式下的圖形形狀，真正打好學生對于圖形旋轉變換題的認知基礎.

二、證明線段之間的相關數量關系

例2如圖2，已知三角形ABC中AC=BC，∠C=90°，D是AB上任一點，DB2+AD2=2CD2.

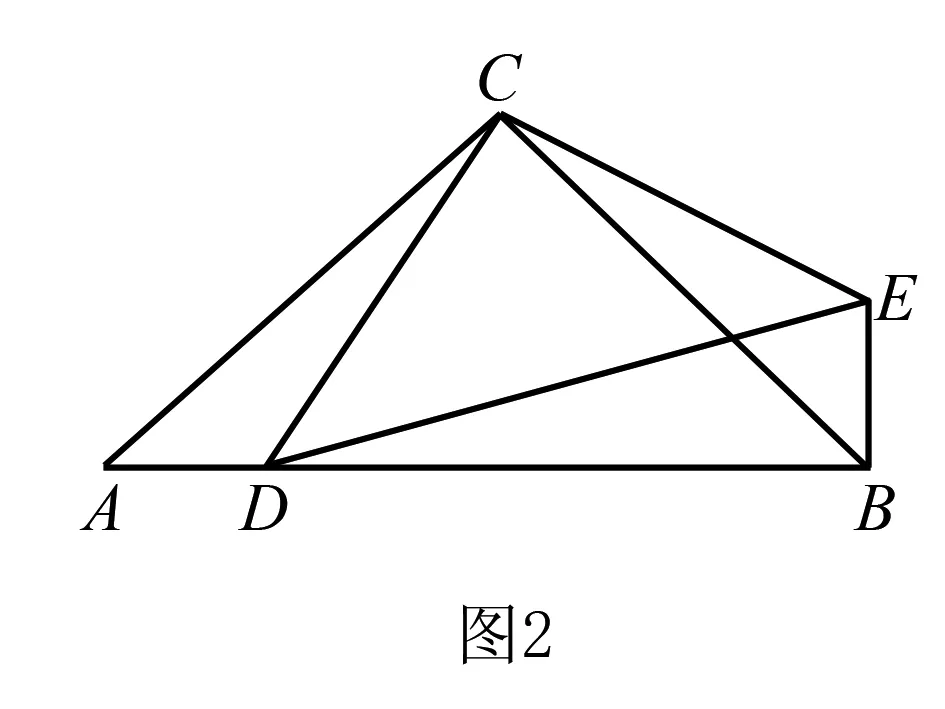
對于這道題目的解答，教師要引導學生抓住旋轉變換題目的解題關鍵就是旋轉后圖形與旋轉前圖形屬于全等關系.由此利用好旋轉角度的變化特點，通過化歸思想解決問題.其具體解題步驟是這樣的――先將三角形ACD繞C點逆時針旋轉90度后再連接線段ED，得出三角形BDE是直角三角形，而三角形CDE則是等腰直角三角形.將分散的線段劃歸到兩個直角三角形中，最后由勾股定理得到ED2=CD2+CE2=2CD2.

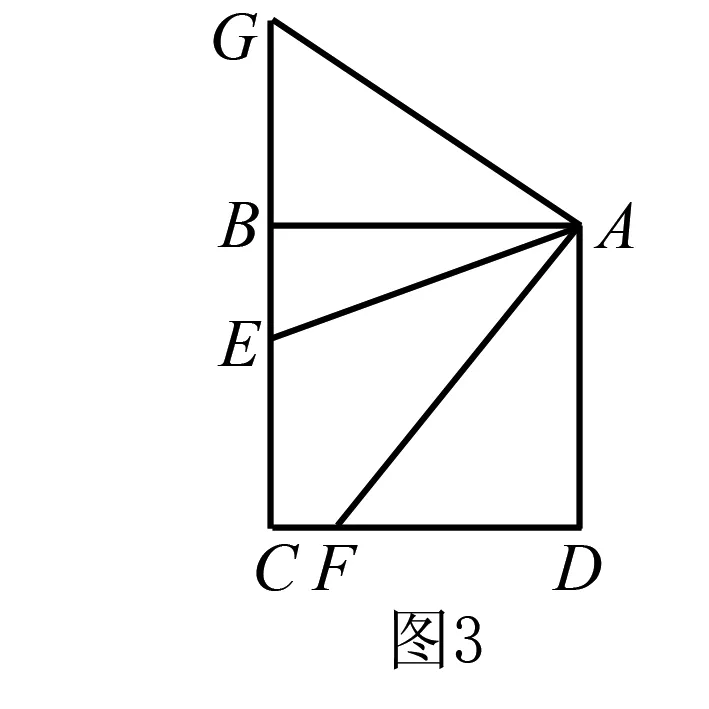
例3如圖3，已知正方形ABCD，E為BC上任一點，且AE=BE+FD交CD于F點，證明AF平分∠DAE.

這道題目的解題要點仍和上道題目一樣，也是將三角形ADF圍繞A點進行旋轉的.由此可以得知三角形中AE=EC=BE+FD.再利用好正方形的相關性質得出∠DAF與∠FAE相等，最終通過旋轉變化解答.教師在教學時應幫助學生尋找到旋轉過程中變與不變的量，攻克線段數量關系變換，從而達到解題目的.

圖形旋轉變換題是新課改以后，圖形與幾何部分知識的重要考察內容，教師在淡化證明過程時也應該加強學生對于圖形旋轉變換題的了解.培養學生的空間素養，讓學生知曉不同圖形旋轉變換題的解題關鍵.融入合適的數學知識點，幫助學生建立數學知識的學習脈絡.重視學生的已有經驗，讓學生在自主探究過程中了解圖形旋轉變換題的真正解題技巧.