基于相位幅值調制的聚苯乙烯小球非接觸傳輸

張 鵬，董惠娟，初紅霞，杜 娟，吳東艷

(1.黑龍江工程學院 電氣與信息工程學院，哈爾濱 150050；2.哈爾濱工業大學 機電工程學院，哈爾濱 150001)

在生物學、分析化學、醫藥學等領域，非接觸傳輸處理小顆粒和液滴得到了非常廣泛的應用[1-4]。在眾多的非接觸處理技術中，聲懸浮因其具有生物兼容性、被懸浮材料的獨立性以及不需要對實驗樣品制備而得到廣泛關注和研究[5]。用于非接觸傳輸和處理物體的聲懸浮器通常由1個或多個超聲換能器和反射面組成[6]。當物體被穩定懸浮在懸浮器中時，可以通過改變超聲換能器的電參數、懸浮器的聲腔幾何參數以及懸浮器本身或換能器的空間位置等方法來實現被懸浮物體的二維或三維可控移動[7]。FORESTI D等[8]使用一種由多個換能器組成的平面陣列，通過改變兩個相鄰換能器之間驅動電壓的幅值，實現物體在空氣中的水平傳輸。文章基于平面陣列式懸浮器，描述一種使用相位幅值調制(Phase and Amplitude Modulation，PAM)的驅動換能器陣元，實現被懸浮物體的水平平滑移動的方法。與單純使用幅值調制的傳輸方法相比，通過同時改變換能器陣列中相鄰陣元間驅動信號的相位差和幅值的方式，可使樣本的傳輸過程更加平滑和穩定。文中對相位和幅值混合調制方法進行有限元仿真和實驗研究，實現了聚苯乙烯小球在空氣中的可控平滑移動。

1 數值模型

文中所使用的平面陣列式聲懸浮器由5個諧振頻率為f=20 kHz的郎之萬壓電超聲換能器(Langevin Piezoelectric Transducer，LPT)和一個不銹鋼反射面組成。超聲換能器輻射面被設計成邊長為D=15 mm的正方形，其輻射端材料為鈦合金。5個超聲換能器構成1×5水平線性陣列。該聲懸浮器的二維簡化ANSYS仿真模型如圖1所示。

圖1 1×5平面陣列式聲懸浮器模型

圖1中，坐標x表示水平方向，H為換能器陣輻射面與反射面之間的距離。W=90 mm為反射面的寬度。S為換能器陣元間距，被設定為0.5 mm。模型使用在x和z兩個方向上具有位移自由度的結構單元構建輻射面和反射面，使用只具有聲壓自由度的聲流單元來仿真輻射面和反射面之間的空氣區域。對于空氣區域與輻/反射面之間的相互作用問題，則使用具有位移和壓力兩個自由度的流固單元來解決。這些單元被應用在空氣和輻/反射面之間，并通過在其接觸面添加流固耦合標志(FSI)來仿真流固耦合問題。在陣元間隙處以及無結構覆蓋的聲場邊界處使用無反射全吸收邊界條件來仿真無限遠空氣區域。仿真中用到的換能器輻射面振幅由激光測振儀(OFV-505/500)測量獲得，為12 μm。

在聲懸浮器中，小尺寸物體會被捕獲并懸浮在聲場的勢能極小值點處，而作用在小球上的聲輻射力的時間平均聲懸浮勢能由式(1)給出[9]。

(1)

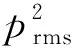
在ANSYS中，通過對有限元模型進行仿真計算，可以得到輻射面和反射面之間空氣聲場內的聲壓p分布。而式(1)中所需的空氣質點振動速度v則可使用式(2)進行計算。

v=-▽p/(jωρ).

(2)

為了得到與被懸浮小球半徑無關的懸浮勢能，定義相對聲輻射勢能為

(3)

作用在被懸浮小球上的聲輻射力F由式(4)計算得到，其相對聲輻射力Fri則由式(5)計算得到。

Fi=-?U/?xi，

(4)

Fri=-?Uri/?xi.

(5)

式中：i表示第i個方向。

聲輻射力在豎直方向的分量Fz用來克服使小球懸浮起來的重力，其水平方向的分量Fx則用來確定小球的水平懸浮位置。顯然，在水平方向上，小球會懸浮在Fx=0的點上。同時，Fx還可以作為控制物體水平移動的推進力。當懸浮勢能的節點位置發生水平移動時，懸浮的小球也會在這個水平分量Fx的作用下，跟隨懸浮勢能節點移動。

2 幅值調制傳輸過程分析

文中所述的1×5平面陣列式聲懸浮器中，每個換能器均由一路幅值、相位、頻率可編程設定的超聲信號驅動[10]。依據FORESTI D等[8]的研究，當5個換能器的驅動信號電壓幅值按照圖2所示的規律變化且驅動信號的相位差Δφ始終為0°時，可以實現物體從LPT1傳輸到LPT5。整個傳輸過程可分為4個傳輸階段。在每個傳輸階段內，只有2個相鄰換能器振動。

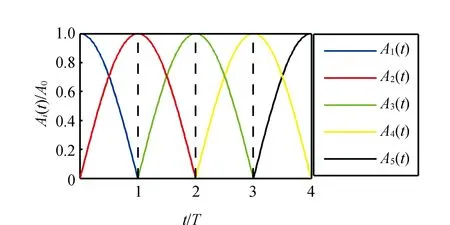
圖2 5個超聲換能器驅動信號的幅值變化

圖2中，T為超聲換能器驅動信號電壓幅值的調制周期，指懸浮勢能節點從1個換能器的軸線處移動到相鄰換能器的軸線處所需的時間。Ai(t)表示第i個LPT的驅動信號電壓幅值函數，其表達式為

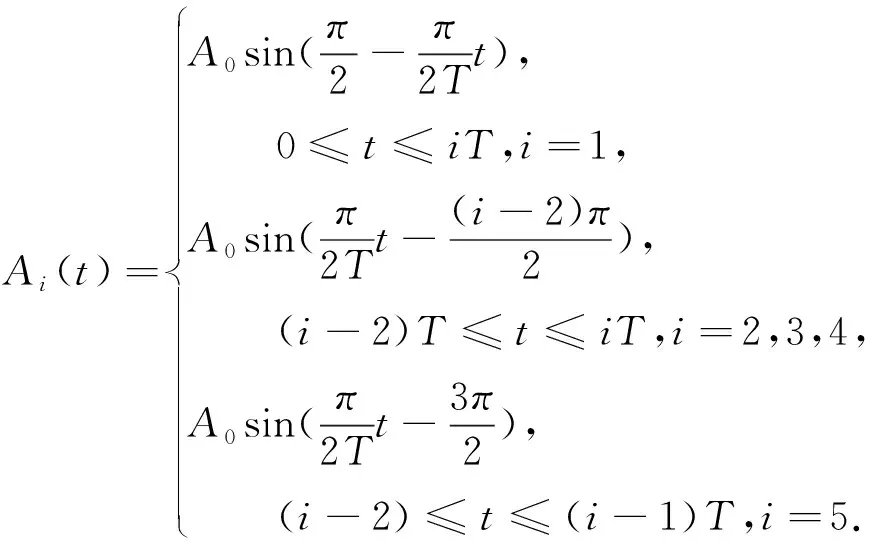
(6)

圖3給出使用上述驅動方法時，聚苯乙烯小球水平位置變化情況的仿真(藍色圓圈)和實驗(紅色)曲線。其中，仿真曲線是通過對數值模型的仿真計算，獲取相對聲懸浮勢能節點的坐標。在仿真和實驗中，取換能器輻射面到反射面的距離為H=0.5λ，換能器輻射面振動頻率為f=20 kHz。聚苯乙烯泡沫小球的直徑為3 mm，調制周期T=4 s。

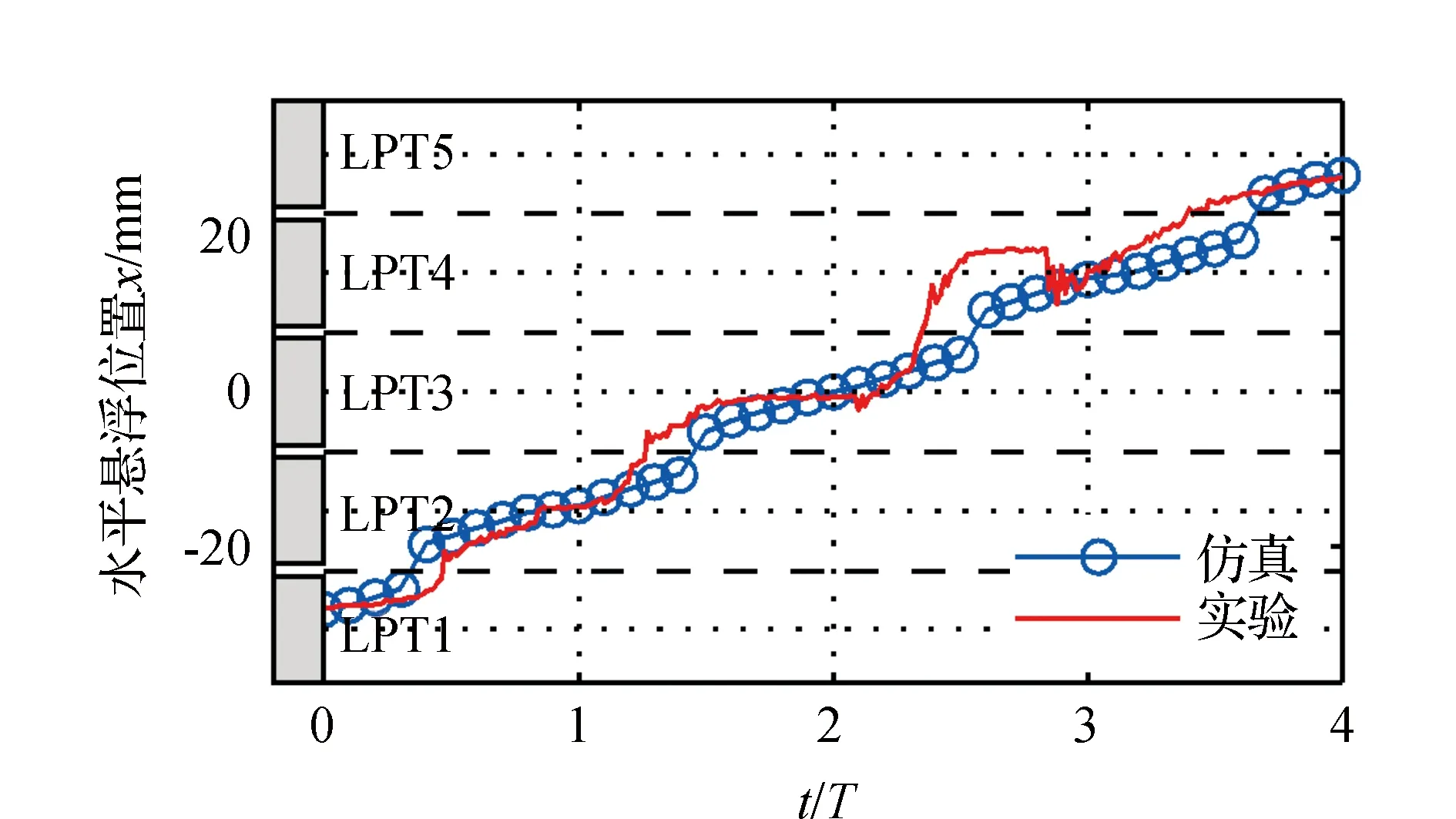
圖3 聚苯乙烯泡沫小球水平傳輸的仿真和實驗結果曲線(S=0.5 mm,f=20 kHz,A0=12 μm,H=0.5λ,T=4 s)

從圖3可以看出，聚苯乙烯泡沫小球從LPT1傳輸到LPT5。小球的實驗運動趨勢與仿真結果基本吻合。小球在傳輸過程中有跳躍傳輸和振蕩的現象發生，這種現象多發生在小球經過相鄰LPT間隙的時刻。這是由于陣元間隙的存在和聲場的不對稱，改變了間隙下方的聲場，使間隙下方無法形成穩定的懸浮勢能節點，小球無法停留在間隙下方，而跳躍到相鄰LPT下方。表1列出在使用幅值驅動方法條件下，不同傳輸階段小球通過間隙時的跳躍傳輸距離Ds和振蕩幅值Aosc。

從表1可以看出，在整個懸浮傳輸過程中，小球的最大跳躍傳輸距離為7.70 mm，最大振蕩幅值為2.37 mm。跳躍傳輸距離越大，則對應的振蕩幅值越大。顯然，降低跳躍傳輸距離可以減少振蕩幅值。值得注意的是，在傳輸階段2T～3T，發生大幅跳躍傳輸和回跳振蕩現象等不穩定傳輸現象，這是由裝配誤差以及LPT3和LPT4的諧振頻差造成的聲場分布不均勻而導致的。

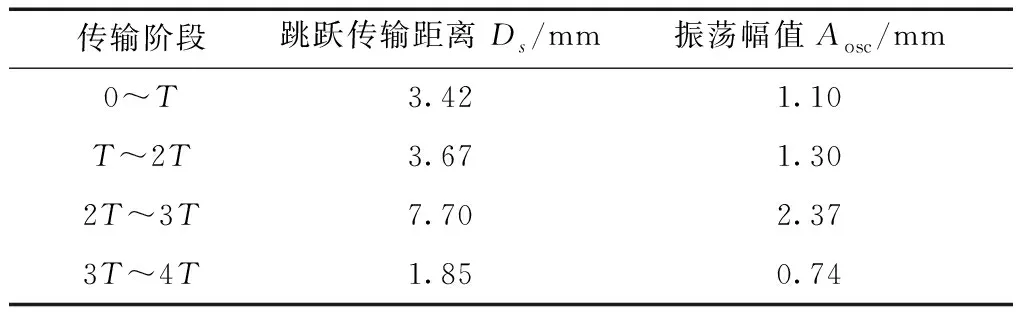
表1 使用幅值驅動方法時不同傳輸階段小球通過間隙時的跳躍傳輸距離Ds和振蕩幅值Aosc

3 相位對傳輸過程的影響

小球在傳輸過程中發生的跳躍和振蕩現象會降低傳輸穩定性。實踐表明，驅動信號的相位差可以改變聲場中的懸浮勢能分布，進而改變物體在聲場中的懸浮位置。圖4給出不同傳輸階段相鄰兩個換能器驅動信號相位差為0°、±20°、±40°、±60°時，小球的水平懸浮位置仿真曲線。

從圖4(a)、圖4(d)可以看出，在傳輸階段0～T和 3T～4T，水平懸浮位置變化規律相似。對于傳輸階段0～T(見圖4(a))，當Δφ12<0°時(LPT1的相位超前于LPT2)，水平懸浮位置曲線線性度較差，且偏離Δφ12=0°時的水平懸浮位置。相位差絕對值|Δφ12|越大，偏離現象越嚴重。當Δφ12>0°時，水平懸浮位置曲線線性度較好，跳躍傳輸改善情況明顯。對于傳輸階段3T～4T(見圖4(d))，相位對水平懸浮位置的影響情況與階段0～T相反。當Δφ45<0°時，水平懸浮位置曲線線性度較好。從圖4(b)、圖4(c)可以看出，傳輸階段T～2T和2T～3T，水平懸浮位置變化規律相似。相位對傳輸跳躍現象改善不明顯。當|Δφ23|和|Δφ34|大于等于20°時，水平懸浮位置偏離其0°時的曲線較嚴重。

表2列出相位差為0°、±20°、±40°、±60°時，不同傳輸階段內，小球通過間隙時跳躍傳輸距離Ds的仿真數值。為了提高傳輸過程的穩定性，Ds應該越小越好。在4個傳輸階段內，Ds的最小值分別為2.99 mm、5.47 mm、5.48 mm、2.99 mm，對應的相位差為40°、20°、-20°、-40°。

圖4和表2可以確定，最優相位差Δφopt在4個傳輸階段內的最佳取值范圍分別是20°<Δφopt12<60°,0°<Δφopt23<20°，-20°<Δφopt34<0°，-60°<Δφopt45<-20°。同時，由于聲懸浮器的結構對稱，可得Δφopt12=-Δφopt45，Δφopt23=-Δφopt34。

表2 相位差為0°、±20°、±40°、±60°時，不同傳輸階段內小球跳躍傳輸距離Ds仿真結果 mm

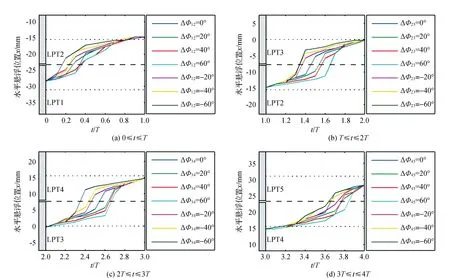
圖4 小球的水平懸浮位置仿真曲線

為了得到不同傳輸階段的最優相位差Δφopt，在相位差最佳取值范圍內，對小球在傳輸過程0～T和T～2T中的跳躍傳輸距離Ds進行仿真，仿真結果見圖5。

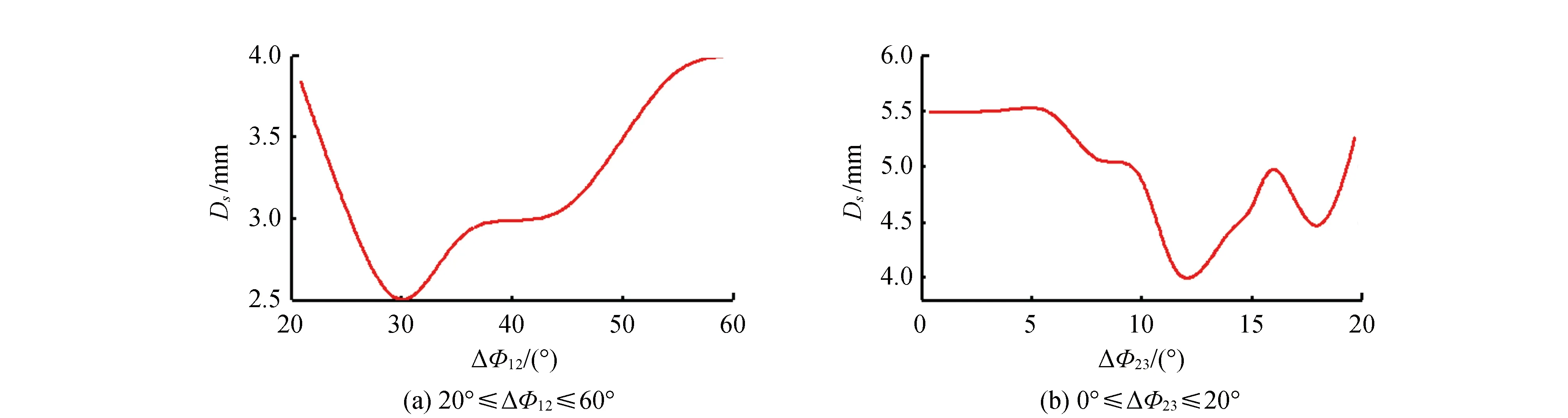
圖5 0～T和T～2T傳輸階段驅動信號相位差最佳取值范圍內小球的跳躍傳輸距離仿真結果

由圖5可知，0～T和T～2T階段，相位差的最優值為Δφopt12=30°，Δφopt23=12°，此時物體的跳躍傳輸距離的仿真值最小，分別為Ds=2.5 mm、3.98 mm。比相位差為Δφ=0°時的跳躍傳輸距離分別減少了58.3%、27.5%。同時，可以確定2T～3T和3T～4T階段的最優相位差分別為Δφopt34=-12°，Δφopt45=-30°。

4 聚苯乙烯小球的混合調制傳輸

依據上述仿真結果，設置傳輸過程中相鄰換能器驅動信號相位差的變化情況如圖6所示。

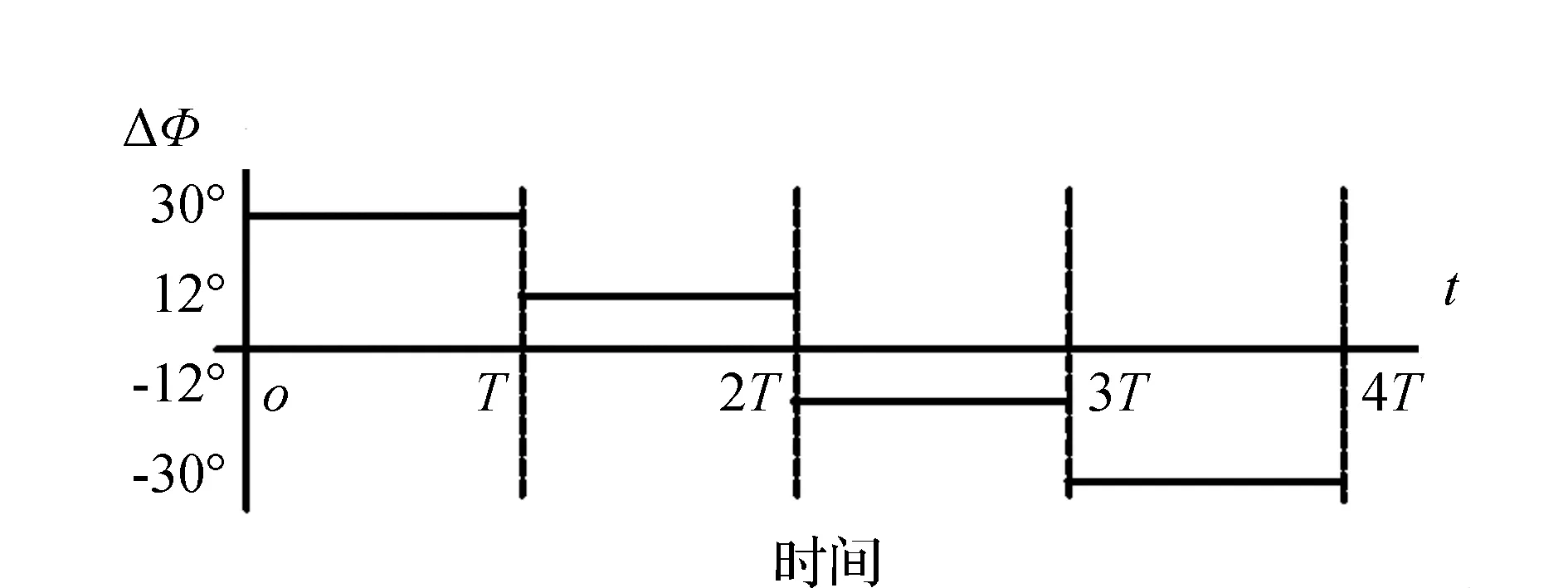
圖6 傳輸過程中相鄰換能器驅動信號相位差的變化情況

圖7給出使用PAM驅動方法獲得的聚苯乙烯泡沫小球水平懸浮位置的實驗和仿真曲線。表3列出在使用PAM驅動方法條件下，不同傳輸階段中，小球通過間隙時的跳躍傳輸距離Ds和振蕩幅值Aosc以及相對于幅值驅動方法Ds和Aosc的減少比率。

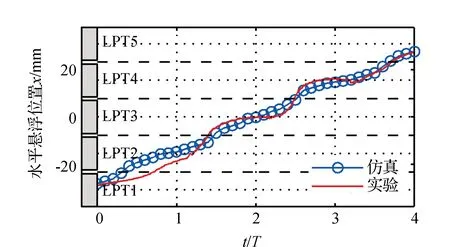
圖7 使用相位幅值調制驅動方法得到的聚苯乙烯泡沫小球水平傳輸的仿真和實驗結果曲線

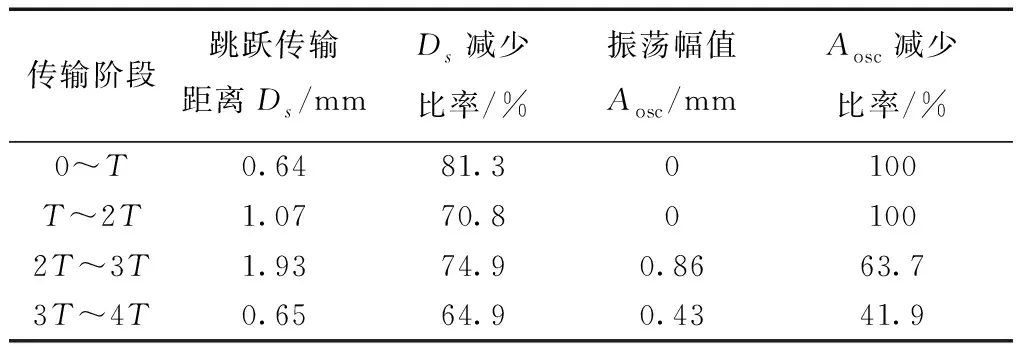
表3 使用PAM驅動方法條件下不同傳輸階段小球的跳躍傳輸距離Ds和振蕩幅值Aosc

由圖7和表3可得，使用PAM方法可以有效改善傳輸過程中小球的跳躍和振蕩現象。由于懸浮器的結構并沒有改變，大幅跳躍傳輸和回跳振蕩現象仍然發生在2T～3T傳輸階段。在4個傳輸階段中，Ds和Aosc的最大減少比率為81.3%和100%。在傳輸階段0～T和T～2T,振蕩現象消失。

5 結束語

在超聲懸浮傳輸過程中，被懸浮物體在聲輻射力的作用下，跟隨懸浮勢能節點移動。為了保證物體的傳輸穩定性，需要構建穩定連續的懸浮傳輸聲場。對于文中所述的1×5平面陣列式超聲懸浮器，陣元間隙、裝配誤差以及換能器陣元諧振頻差等因素均會影響傳輸聲場的連續和穩定，從而導致物體在傳輸過程中發生跳躍和振蕩現象。為了提高小球在懸浮器中的傳輸穩定性，減弱甚至消除小球在傳輸過程中的跳躍和振蕩現象，文中在傳統的換能器陣元幅值調制驅動方法的基礎上，提出一種相位和幅值混合調制的換能器陣元驅動方法。該方法引入相鄰換能器驅動信號相位差作為輔助控制參量來補償因換能器陣元間隙等因素導致的聲場分布不均，顯著減少了小球在傳輸過程中的跳躍傳輸距離和振蕩幅值，提高了小球的傳輸穩定性。文中分析了幅值調制傳輸過程中小球的跳躍和振蕩情況，并通過仿真確定不同傳輸階段下，相鄰換能器驅動信號的最優相位差。實驗表明，懸浮傳輸過程中，物體的跳躍傳輸距離和振蕩幅值分別減少了64.9%和41.9%。