基于模型檢查的民用飛機飛控系統安全性評估

范基坪 洪驥宇

(上海飛機設計研究院，上海 201210)

0 引言

基于ARP 4754A[1]，ARP 4761[2]的傳統安全性評估流程在民用航空領域已經得到了廣泛的應用。然而，近20年來計算機科學與集成電路制造工藝的發展促使了產品機電系統的深度融合，嵌入式軟件控制方式逐漸代替傳統的機械控制，系統復雜度急劇上升。傳統安全性評估流程嚴重依賴于安全分析人員的經驗，面對新型安全關鍵系統軟硬件深度集成，復雜度高的特征時，面臨著系統描述能力不足、分析結果不準確、分析工作迭代困難等問題[3-4]。

針對系統安全性研制流程中產生的新問題，在系統工程思想指導下，一種面向基于模型的系統工程的新型安全性評估理念[5-8]——基于模型的安全性評估(Model-Based Safety Assessment, 簡稱MBSA)，得到了學術界與工業界的廣泛認可。在基于模型的安全性評估過程中，安全性要求的評估通過模型檢查等形式化方法自動實現[9-10]。通過在安全性評估過程中引入形式化的模型與規范，將評估過程轉化為系統模型的規范驗證過程。

本文采用當前MBSA研究領域較為成熟的模型檢查方法，針對模型檢查的建模特點，基于SMV語言提出安全性建模與規約方法。以某延程型寬體客機飛控系統為對象，構建該機型飛控系統的功能模型，并定義形式化的安全性要求，開展安全性評估，從而驗證基于形式化方法的安全性評估在民機系統安全性工作中的可行性。

1 模型檢查的基本內涵

模型檢查是形式化方法的重要分支[11]，基本思想是利用時態邏輯描述目標系統所需滿足的性質φ，有限狀態機(FSM)描述系統的狀態轉移關系s，以及模型檢查的算法遍歷FSM來檢驗時態邏輯公式的正確性，即s╞φ，如圖1所示。對不滿足的系統規范，可以得到一個反例，說明系統不滿足要求的狀態路徑。

圖1 模型檢查基本原理

模型檢查所構建的系統模型往往并非目標系統實際所采用的建模形式，因此必須將目標系統轉換為某一模型檢查工具所支持的輸入形式。構建系統模型時需要結合待驗證的屬性對系統進行必要的抽象和簡化。建模時抽象度過高會導致模型與真實系統差別增大，導致驗證工作漏掉某些真正的錯誤，而抽象程度過低則會增加驗證模型的復雜性，因此對模型抽象的過程在整個模型檢查過程中需要占用大量的時間。

1.1 有限狀態機

模型檢查中系統模型的有限狀態機稱為Kripke結構。Kripke結構是一種嚴格的數學結構，是狀態轉移圖的一種變形，能夠很好地描述系統的狀態轉移及時序邏輯關系。典型Kriple結構是一個五元組：

M=

其中：S是有限狀態集合，S0?S是初始狀態集合，R表示狀態轉移關系，R?S×S，L:S→2AP稱為標記函數，用于標記每個狀態中成立的所有原子命題集合，AP是所有原子命題與其否命題的集合，該集合是AP的一個子集。

在一個Kripke結構M中，從任意某一狀態s開始產生的無限長的狀態序列n=s0s1s2...被稱為該結構中的一條路徑，該路徑中s0=s，對所有i≥0，都有R(si,si+1)成立。系統動態運行中的屬性通常描述為一系列原子命題的動態滿足過程。

圖2左邊為一個簡單Kripke結構的示例，圓表示狀態，箭頭線代表狀態轉移關系，箭頭兩端的狀態及轉移的首位兩個狀態，沒有起始端的箭頭表示系統進入初始狀態，狀態內標注的原子命題組成Kripke的標記函數，當某一狀態激活時，狀態內的原子命題成立。

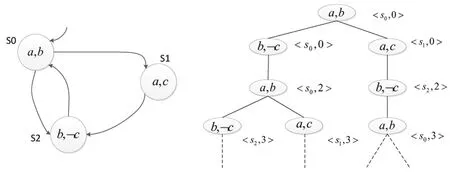
圖2 簡單Kripke結構示例

對于該Kripke結構，S={so,s1,s2}，S0={so}，AP={a,b,c,a,b,c}，R={,,,}，L(s0)={a,b}，L(s1)={a,c}，L(s2)={b,c}，將系統狀態關系展開得到圖2右側所示結構。

可以得出以下結論，Kripke結構的狀態關系展開類似樹狀結構，除去根節點外，每一節點僅有一個前端節點，可以任意訪問其后端節點，從而構成一棵無限深度的樹。

1.2 時態邏輯

時態邏輯公式是模型檢查中用于描述動態系統屬性的形式化命題方法。常見的時態邏輯包括兩種：線性時態邏輯(linear temporal logic，簡稱LTL)與計算樹邏輯(computation tree logic，簡稱CTL)。

線性時態邏輯將系統時間定義為無限長的時態序列，稱為計算路徑，當前時刻存在唯一的下一時刻狀態，對于存在多種未來狀態的系統，利用一組路徑表示不同的時態序列。線性時態邏輯命題由時態算子與原子命題組成。常用時態邏輯算子包括：

G(Glabal)：未來所有狀態；F(Final)：未來某個狀態；X(neXt)：下一個狀態；U(Until)：直到…都；R(Release)：直到…才；W(Wait)：弱…直到。

線性時態邏輯無法描述多條路徑之間的相互關系，在描述分支并發系統時，采用計算樹邏輯描述系統時間特性。計算樹邏輯以Kripke初始節點為根節點，將Kripke結構展開為無線樹形結構，相比線型時態邏輯，計算樹定義路徑量詞A(對于所有路徑)與E(存在一條路徑)，且不存在時態算子R、W。

2 系統建模方法及安全屬性定義

2.1 系統模型構建方法

不同模型檢查工具對應不同的自動機語言，構建系統模型時需要根據特定語言的特點確定模型結構與部件描述方式。以SMV為例，構建系統SMV模型的基本步驟如下：

1)確定目標系統的基本結構，包括系統層次劃分與同一層次的部件，為每個部件及系統層級定義Module，按照系統自上而下結構從模型main模塊開始逐層實例化。

2)根據部件內部工作情況與部件間接口關系，定義各個模塊所需內部變量及類型，確定每個模塊輸入變量。系統模型的狀態空間規模由變量數量決定，在定義變量過程中應盡量減少冗余變量。

3)在每個模塊的ASSIGN及DEFINE部分定義系統行為。根據MBSA模型構建的兩種策略，失效建模分為名義系統+故障注入以及直接失效行為兩種，圖3和圖4分別描述了兩種建模方式。名義系統+故障注入的方式將部件模型分為名義模塊nominal_comp與失效模塊failure_comp兩部分，在另一模塊extend_comp中實例化兩類模塊，根據部件狀態調用nominal_comp與failure_comp中參數值；直接故障行為描述則在同一模塊中同時定義正常與失效狀態輸出。

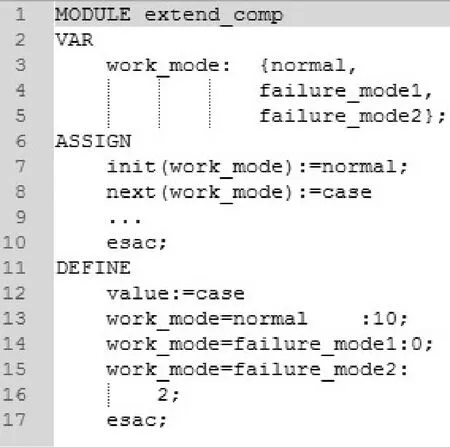
圖3 直接系統建模

2.2 安全屬性的定義

傳統安全性評估過程中，通過FHA確定初始安全性要求，并在研制流程中逐漸細化分解。模型檢查的驗證與分析工作在原有研制流程基礎上開展，通用自動化檢驗是否滿足安全屬性來判斷系統的安全性水平。系統安全屬性的來源包括：FHA結論，初步故障樹結論及FMEA，前一階段模型檢查所得結論等。

將已知的安全性需求形式化表示為時態邏輯命題，要針對時態邏輯命題所涉及的部件，在模塊中定義相應原子命題的標識變量。以圖4為例，如果需要定義安全屬性為：部件在failure_mode1時value值不能低于5，利用CTL公式可以定義為：

AG (work=failure_mode1 >failure_comp.value>=5)

選擇CTL或者LTL的基本原則是依據命題的描述特性。對于存在類型的命題，例如證明系統能否到達某一狀態，可以采用CTL描述特性；對于強調狀態序列特性的問題，例如某些狀態的先后次序，可以采用LTL描述。

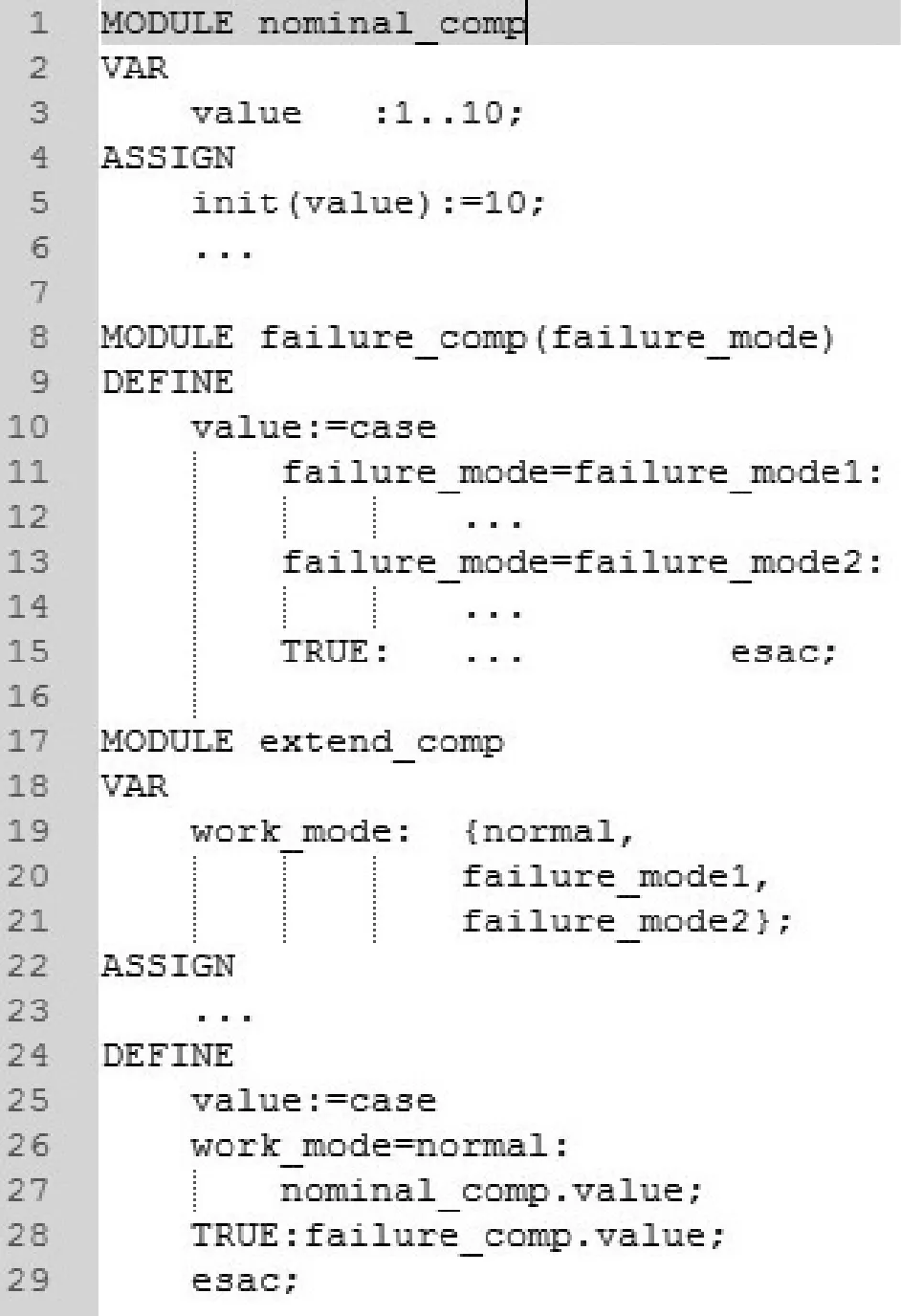
圖4 名義系統建模+故障注入

3 某民用飛機案例驗證

3.1 民機飛控系統

某民用飛機采用電傳+機械的組合控制模式，其功能控制模型是軟件、硬件、機電結構高度綜合的復雜系統，以副翼控制功能為例，考慮影響副翼控制功能的飛控部件，簡化飛控系統功能模型如圖5所示。

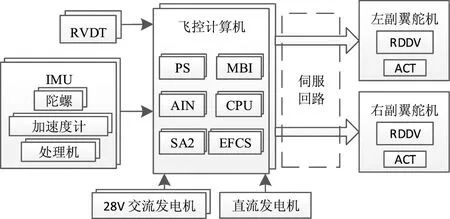
圖5 典型民用飛機飛控系統簡化功能框圖

桿位移傳感器、慣性測量組件將動作數據及測量數據輸入至飛控計算機，由飛控計算機解算得到的相應控制信號經伺服放大回路輸出值左右副翼舵機。28 V交流發電機與永磁發電機為飛控計算機供電。建立系統模型時，考慮飛機在AFCS、DDC、EFCS三種工作狀態下的部件接口關系差異，其中飛控計算EFCS板僅在EFCS模式下運行，DDC模式下MBI與AIN板工作狀態對副翼控制功能無影響。根據系統描述構建SMV模型，圖6所示為飛控計算機MBI板SMV模塊示例。

圖6 飛控計算機MBI板模型

定義系統安全屬性為左右副翼舵機不能同時進入失效狀態，將命題形式化描述如下：

AG!(left_servo.status=failure&right_servo.status=failure)

3.2 NuSMV仿真

模型檢查在檢測系統規范時會遍歷系統狀態空間，基于BDD的NuSMV模型檢查器目前能夠支持2120的狀態空間，但是運算時間會隨著系統狀態空間的擴大迅速增加。因此在執行系統規范的嚴格檢查之前，運用仿真方式模擬系統狀態變化路徑，對系統行為進行初步的分析。案例所建系統包含69個變量，系統可達狀態數達到263次。通過仿真尋找系統失效路徑，圖7所示為其中一條包含50個仿真步長單位的系統失效路徑。

圖7 一條仿真狀態路徑

圖7所示的一條狀態路徑展現了一個特定失效場景，State1.1為系統初始狀態，飛控系統處于PFCS工作模態，部件運行正常，State1.2時28 V發電機發生失效，State1.18時系統進入DDC工作模態，慣性測量組件失效對系統功能無影響，State1.51時右副翼舵機失效。

3.3 系統規范驗證

NuSMV系統模塊運行方式分為同步與異步兩類，模型檢查及仿真過程中狀態空間與模塊運行方式有關，在驗證系統規范時，采用同步運行方式以降低狀態空間規模，提高檢查效率。在NuSMV Shell中執行：

check_ctlspec & show_property

命令得到規范檢查結果如圖8所示。

圖8 副翼控制功能反例

檢查發現命題：

AG !(left_servo.status=failure&right_servo.status=failure)

是錯誤的，分析生成的反例可知系統在EFCS模式下發生了EFCS板的同時失效，此時可以根據系統反例所描述的失效場景通過限制條件的異步仿真尋找EFCS板同時失效的原因。

4 結論

本文針對模型檢查器NuSMV的特點，提出基于SMV語言的安全性模型構建思路，闡述了系統規范的來源與實現方式，并通過典型民用飛機電傳飛控系統案例演示利用NuSMV建模與屬性驗證過程。

NuSMV作為最經典的模型檢查工具，基于BDD的運算方法雖然提高了執行效率與建模規模，但仍在定量計算、反例優化等方面存在局限。作為MBSA的核心工作，如何協調安全評估與模型檢查的關系仍然值得研究。