如何設計科學、有效、有趣的教育游戲

張露 胡若楠 曾嘉靈 尚俊杰

[摘? ?要] 近年來，教育技術(shù)的發(fā)展為創(chuàng)新學習方式帶來了前所未有的機遇。針對游戲化學習研究領域的核心問題——如何設計科學、有效、有趣的教育游戲，以學習科學的跨學科為視角設計了數(shù)學游戲《分數(shù)跑跑跑》。在認知內(nèi)容設計方面，依據(jù)認知神經(jīng)科學、教育學、心理學等領域的相關(guān)研究成果展開設計，為學習者提供科學的認知支持;同時以實踐需求作為設計導向，確保游戲使用的有效性。在保障科學性和有效性的基礎上，借助游戲元素充分調(diào)動學習者情緒動機狀態(tài)。經(jīng)檢驗，《分數(shù)跑跑跑》能夠顯著提高小學四年級學生的分數(shù)概念性知識水平。

[關(guān)鍵詞] 教育游戲; 游戲化學習; 學習科學; 數(shù)學認知; 設計研究

[中圖分類號] G434? ? ? ? ? ? [文獻標志碼] A

[作者簡介] 張露（1992—），女，黑龍江鶴崗人。講師，博士，主要從事游戲化學習、數(shù)學認知、學習科學與技術(shù)設計研究。E-mail：zhanglu1176@163.com。尚俊杰為通訊作者，E-mail：jjshang@pku.edu.cn。

一、引? ?言

近年來，教師和研究人員逐漸意識到游戲化學習的潛在優(yōu)勢，嘗試使用游戲作為教學指導和興趣激發(fā)的工具[1-3]。國內(nèi)外游戲化學習研究領域高度重視教育游戲的設計與開發(fā)[4]，如何設計科學、有效、有趣的教育游戲成為教育游戲研究的關(guān)鍵問題。隨著教育領域基礎研究的深入、教育技術(shù)的不斷創(chuàng)新，學習科學這一跨學科領域得以快速發(fā)展。學習科學立足教學實踐，在探索“人是如何學習的”這一問題的過程中，以跨學科的視角致力于闡釋學習的發(fā)生機制，分析過程中的學習行為，并借助教育技術(shù)進行學習環(huán)境的設計。學習科學的研究成果和理論發(fā)現(xiàn)也為教育游戲的設計提供了嶄新的視角。義務教育階段的數(shù)學教育一直是游戲化學習的重要應用領域。在數(shù)學認知研究領域，分數(shù)學習在兒童的數(shù)學發(fā)展過程中具有重要意義，分數(shù)學習困難也是普遍存在的現(xiàn)象。信息技術(shù)的發(fā)展為分數(shù)學習創(chuàng)造了更多的可能。隨著移動設備的普及和游戲技術(shù)的進步，教育游戲支持下的分數(shù)學習成為一種趨勢，備受教育研究者和實踐者的關(guān)注。

二、分數(shù)游戲的整體設計框架

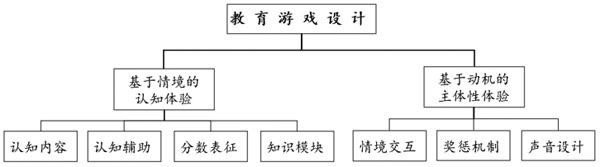
為了實現(xiàn)科學、有效、有趣的游戲設計，游戲化學習的理論框架是產(chǎn)品設計的基礎。在游戲設計之前，筆者已通過相關(guān)理論要素的推演和歸納，提出了游戲化學習體驗的理論框架，歸納了游戲化學習體驗的三大范疇，即基于情境的認知體驗、基于協(xié)作的社會性體驗、基于動機的主體性體驗。在基于情境的認知體驗范疇內(nèi)，游戲化學習環(huán)境可以為學習者提供認知真實性的虛擬學習環(huán)境，借助與學習環(huán)境的互動與反饋，學習者可以進行知識建構(gòu)[5]。基于協(xié)作的社會性體驗主要包含學習者在游戲化學習過程中收獲的協(xié)作體驗和學習指導。基于動機的主體性體驗是在社會認知理論的主體性視角（Agentic Perspective）的啟發(fā)下[6]，主要關(guān)注學習者個體的動機、情緒、意愿狀態(tài)的主體性體驗。依據(jù)游戲化學習體驗框架，本研究在基于情境的認知體驗和基于動機的主體性體驗兩個維度確定了分數(shù)游戲的設計體系。

基于情境的認知體驗主要涉及分數(shù)游戲的教育性認知內(nèi)容，以實現(xiàn)教育游戲的教育功能為目標。在該范疇內(nèi)，游戲設計模塊包含游戲的核心認知內(nèi)容、認知輔助工具、表征方式以及難度梯度的設計，內(nèi)含邏輯線索為“學什么—怎么學—如何呈現(xiàn)—怎樣進階”。基于動機的主體性體驗主要涉及游戲化元素為學習者帶來的愉悅體驗，關(guān)注教育游戲的娛樂功能。在該范疇內(nèi)，游戲設計模塊包含游戲情境與交互設計、獎懲機制和聲音的設計。游戲的整體設計框架如圖1所示。由于教育功能是教育游戲的首要功能，因此，游戲元素的設計服務于認知內(nèi)容的呈現(xiàn)。

教育游戲在設計之初，需要明確使用目的，這有助于實現(xiàn)教育游戲的有效性。在游戲使用定位方面，本研究的游戲設計旨在輔助教育教學，作為一款注重數(shù)學意義建構(gòu)的練習游戲，將會成為課堂教學之外的補充。

三、認知內(nèi)容的設計與理論參考

（一）核心認知內(nèi)容

為理解兒童的分數(shù)能力發(fā)展，教育學從數(shù)學知識發(fā)展的角度區(qū)分了分數(shù)的概念性知識和程序性知識。分數(shù)的概念性知識是指對分數(shù)符號含義的理解，教育學領域主要聚焦于分數(shù)的兩大基本含義：“部分與整體”（Part and Whole）以及“測量解釋”（Measurement Interpretation）。“部分與整體”是指分數(shù)符號呈現(xiàn)了部分與整體的關(guān)系，這是理解分數(shù)其他含義的基礎。兒童在幼兒園階段已經(jīng)有了“平分”的生活體驗，因此，能夠很容易地掌握這部分內(nèi)容。“測量解釋”是指對分數(shù)數(shù)值大小的理解[7-8]，主要強調(diào)數(shù)字的表達、比較、排序以及將分數(shù)放在數(shù)軸對應的點[9]，其中，數(shù)軸在建構(gòu)分數(shù)的數(shù)值知識方面有廣泛的應用[10]。在心理學研究領域，分數(shù)通常被界定為一組相互關(guān)聯(lián)的子含義，包括“部分與整體”“比”“算子”“商”“測量”[11-12]。學生需要非常熟悉分數(shù)的表征含義，才能對有理數(shù)進行有效認知。

作為神經(jīng)科學和認知心理學的交叉學科，認知神經(jīng)科學是學習科學研究的重要領域[13]，促進了人類對腦學習機制的探索研究。為研究人腦如何認知分數(shù)，Jacob和Nieder通過功能磁共振成像技術(shù)開展了針對分數(shù)表征的適應性實驗（Adaptation Experiment），這項研究表明，符號比率是以抽象的數(shù)值概念在人腦中進行表征[14]。同時，教育學領域的相關(guān)研究也發(fā)現(xiàn)，分數(shù)數(shù)值表達的準確性與分數(shù)計算和數(shù)學成就密切相關(guān)[15]，理解分數(shù)數(shù)值含義的學生能夠更好地記憶分數(shù)的計算步驟[16]。卡耐基梅隆大學分數(shù)學習研究中心的Siegler教授曾提出數(shù)字發(fā)展的整合理論。該理論認為，數(shù)學發(fā)展是數(shù)字認知范圍不斷擴大的過程，分數(shù)在此過程中居于核心地位，而對數(shù)值的理解是鏈接各類數(shù)字知識的基礎[17]。

以學習科學的跨學科為視角，基于教育學、心理學、認知神經(jīng)科學領域?qū)Ψ謹?shù)數(shù)值理解知識的強調(diào)，結(jié)合筆者在前期調(diào)研中所發(fā)現(xiàn)的四年級學生在“測量解釋”知識方面較差的成績表現(xiàn)，本研究確定以分數(shù)概念性知識中的“測量解釋”知識作為游戲的核心目標教學內(nèi)容，以加深兒童分數(shù)概念性知識理解的深度。

（二）核心認知輔助工具

在確定數(shù)學游戲的核心認知內(nèi)容之后，還需進一步設計游戲中的教學支架，即核心認知輔助工具的設計。依據(jù)分數(shù)概念性知識的相關(guān)理論，“測量解釋”的核心是理解分數(shù)在數(shù)軸上的數(shù)值含義。這與認知心理學家發(fā)現(xiàn)的心理數(shù)軸（Mental Number Line，MNL）認知模型相吻合。心理數(shù)軸是為學習初等算數(shù)知識提供的認知模型，兒童需要意識到阿拉伯數(shù)字和數(shù)詞從左到右依次增長，每一個數(shù)字都比前一個數(shù)字多一個數(shù)量。此外，在認知神經(jīng)科學領域，Ischebeck等人采用功能磁共振成像方法探究了距離效應與大腦頂內(nèi)溝激活的關(guān)系，發(fā)現(xiàn)數(shù)字的整體距離與右側(cè)頂內(nèi)溝和枕中回（Middle Occipital Gyrus）的激活水平呈顯著負相關(guān)，只有整體距離能夠調(diào)節(jié)頂內(nèi)溝的激活[18]，這進一步支持了數(shù)軸對于分數(shù)數(shù)值理解的重要性。

參考分數(shù)認知理論關(guān)于數(shù)軸的相關(guān)研究，本研究確定以數(shù)軸作為分數(shù)游戲的核心認知輔助工具。與此同時，參考具身認知理論設計認知輔助工具的交互方式。20世紀80年代以來，“具身”得到了認知神經(jīng)科學、心理學等諸多領域?qū)W科的關(guān)注，對于人腦“鏡像神經(jīng)元”的發(fā)現(xiàn)也為具身認知提供了重要依據(jù)。雖然個體自己沒有進行某一行為，但“鏡像”其他個體的行為就能夠引發(fā)鏡像神經(jīng)元的激活。那么如何利用具身認知方式來進行認知輔助工具的設計？

在游戲中，設置數(shù)軸的核心目的是讓學生掌握數(shù)量大小的方向感，左邊的數(shù)比右邊的數(shù)小，越往右數(shù)字越大。本研究設定數(shù)軸的呈現(xiàn)方式是“數(shù)軸墻”，讓數(shù)軸顯示在一堵障礙墻上，游戲化身能夠直接面對數(shù)軸墻，形成三個平行平面，即學習者平面、游戲化身平面和數(shù)軸墻平面，以此確保學習者、化身、數(shù)軸墻的左右方向的一致性。學習者借助游戲化身進行游戲參與，游戲化身的左右手方向與學習者左右手方向形成映射;在學習者的操控下，游戲化身與數(shù)軸墻進行交互，成為學習者與數(shù)軸墻交互的中介。基本設置內(nèi)容是一根0～1范圍的數(shù)軸，標有刻度0和1，其他刻度的標注依內(nèi)容設計而定。

（三）分數(shù)表征

三重編碼模型是認知神經(jīng)科學領域廣為接受的數(shù)字認知模型。基于數(shù)學認知在行為和腦神經(jīng)機制方面的相關(guān)研究，該理論認為，大腦在進行數(shù)量加工任務時，會使用三種不同功能的編碼對數(shù)量進行表征，包括模擬數(shù)量編碼（Analog Magnitude Code）、聽覺言語編碼（Auditory Verbal Code）、視覺阿拉伯數(shù)字編碼（Visual Arabic Code）。其中，模擬數(shù)量編碼主要是指對代表數(shù)值概念的圖形進行加工，如代表分數(shù)概念的帶有陰影的圖形;聽覺言語編碼是指對分數(shù)文字進行加工，如“三分之一”;視覺阿拉伯數(shù)字編碼是指對阿拉伯數(shù)字的加工，如“1/3”。

在三重編碼模型的理論基礎上，為確保游戲的有效性，筆者對小學數(shù)學教材（人教版、北師大版）進行前期調(diào)研，發(fā)現(xiàn)數(shù)學教材的分數(shù)概念性講授內(nèi)容主要以模擬數(shù)量編碼和視覺阿拉伯數(shù)字編碼為主，并且模擬數(shù)量編碼的分數(shù)圖形以獨立圖形為主（如帶有陰影的圓形或方形），集合圖形為輔（如5片葉子中的2片）。為了兼顧編碼的平衡以及中國小學數(shù)學教材的內(nèi)容特點，游戲兩類編碼的比例設計盡可能匹配教材。

（四）知識模塊框架

依據(jù)前文所述的數(shù)字發(fā)展的整合理論，數(shù)值理解是整合整數(shù)、分數(shù)、小數(shù)認知的關(guān)鍵。以數(shù)值理解的視角看，整數(shù)與分數(shù)一脈相承，都是數(shù)值的符號表達，分數(shù)表達了整數(shù)的可分割性。為了讓兒童在學習分數(shù)之前，借助已有的整數(shù)知識，理解數(shù)值大小的方向性，本研究在分數(shù)內(nèi)容之前設置了4個整數(shù)知識關(guān)卡。不僅可以讓兒童盡快建立新舊知識的聯(lián)系，也可以幫助兒童掌握游戲的玩法。小學數(shù)學教材的分數(shù)概念性知識的主要講授方式是“數(shù)形結(jié)合”，因此，設置了圖形與分數(shù)對應的關(guān)卡，此部分的主要目的是鞏固“部分與整體”知識的學習。接下來，依據(jù)教材的知識點安排，設置了“分子為1的分數(shù)”“分子不為1的分數(shù)”“分數(shù)比較大小”的模塊，具體內(nèi)容見表1。

四、游戲元素的設計與理論參考

在科學性和有效性的基礎上，游戲元素是實現(xiàn)教育游戲趣味性的關(guān)鍵。游戲元素的設計秉承認知中心的原則，圍繞認知內(nèi)容的設計展開，主要涉及游戲情境與交互方式、獎懲機制、聲音設計、故事線設計等，下文主要介紹核心游戲元素的設計。

（一）游戲情境與交互設計

游戲情境與交互設計是教育游戲激發(fā)兒童學習動機的基礎，也是游戲元素設計的核心。內(nèi)在動機理論是游戲情境設計的主要參考。依據(jù)Malone和Lepper提出的游戲內(nèi)在動機理論，挑戰(zhàn)、好奇、控制、幻想能夠影響學習者的內(nèi)在動機;此外，集體動機受到合作、競爭、自尊因素的影響[19]。每一個數(shù)軸墻都是一個挑戰(zhàn)任務，學習者需要通過自身的認知努力，撞擊正確的數(shù)軸點，瞬間擊碎數(shù)軸障礙墻，才能獲得積分繼續(xù)前進。如未能正確撞擊，化身將受到猛烈反彈，并接受相應懲罰。為了適度地激發(fā)兒童的好奇心，數(shù)軸墻的高度高于游戲化身，通過遮擋視線的方式暗示只有完成挑戰(zhàn)才能繼續(xù)新空間的探索。在游戲化身的控制方面，學習者通過鍵盤的上下左右鍵來完全操縱化身，左右鍵控制方向，上下鍵控制速度，任務的成敗完全取決于學習者的認知努力。同時，為了增加游戲的沉浸感，適當激發(fā)兒童對虛擬世界的幻想，游戲還設置了故事線元素，基于數(shù)軸墻的設計，圍繞“綠光水晶墻”“科技水晶墻”“紫色玻璃墻”“森林墻”等展開，通過闖關(guān)獲得寶藏。

（二）獎懲機制

在通過情境與交互激發(fā)學習動機的基礎上，教育游戲需要一套完善的獎懲機制以維持動機水平，增加學習者的情感投入。ARCS動機模型是教育游戲獎懲機制設計的重要理論參考，該理論認為，人的行為取決于感知到的目標的可能性以及主觀價值[20]，影響學生學習動機的因素主要包括“注意”“相關(guān)”“信心”“滿足感”四個方面。在初始階段，認知內(nèi)容和游戲情境能夠引發(fā)兒童的注意和興趣，而信心和滿足感的獲得才能支持持續(xù)的學習行為。不斷試錯有助于獲得信心和滿足感，為了給兒童充足的試錯機會，游戲的每一個關(guān)卡設置了10個數(shù)軸墻，即10個數(shù)軸任務。游戲場景左上角有7顆能量星，為7次試錯機會，每錯一次減少1顆能量星，以此確保每一個關(guān)卡的通關(guān)標準為正確率高于60%。與此同時，游戲為兒童提供多元的教學支架性質(zhì)的方向提示。

學習科學領域的學者已達成共識，學習是認知、情緒與生理層面進行多層次交流的過程。積極的情緒有助于學習，消極情緒將會對學習帶來消極影響。在逐步建立信心與滿足感的過程中，教育游戲還需要通過一定的獎懲機制來調(diào)動學習者的情緒狀態(tài)。研究發(fā)現(xiàn)，積極的情緒有助于促進記憶，例如，讓實驗參與者對照片呈現(xiàn)的愉悅程度進行評價，然后再進行照片內(nèi)容的回憶，研究發(fā)現(xiàn)被試對帶有明顯情緒狀態(tài)的圖像有更加清晰的回憶[21]。

為了能夠最大限度調(diào)動學習者的情緒投入，本研究參考認知神經(jīng)科學領域?qū)﹄S機獎勵的最新研究，在基礎數(shù)軸任務積分的基礎上，設計了“與運氣相關(guān)”的隨機獎勵機制。認知神經(jīng)科學領域發(fā)現(xiàn)，中腦區(qū)域的神經(jīng)遞質(zhì)多巴胺與獎勵活動有關(guān)，當靈長目動物意識到獎勵出現(xiàn)的不確定性，腦中的多巴胺能的釋放會達到峰值[22]。而多巴胺對整個大腦前額葉等腦區(qū)神經(jīng)元的活性有重要影響[23]。因此，游戲設計將隨機獎勵納入積分體系中，隨機加分以隨機金幣形式出現(xiàn)，游戲化身在路上行走的過程中獲得隨機加分，每關(guān)隨機獎勵出現(xiàn)2～4次，獎勵數(shù)值隨機。其他積分要素還包括基礎數(shù)軸任務積分以及剩余能量星。努力相關(guān)積分和運氣相關(guān)積分的綜合獎勵設計旨在激發(fā)大腦多巴胺的分泌，保持游戲的不確定性，充分調(diào)動游戲化學習過程中的學習者情緒狀態(tài)。為了更好地激發(fā)兒童的學習動機，游戲中還設置了積分排行榜的游戲元素，以此激發(fā)兒童的競爭欲望。

（三）聲音設計

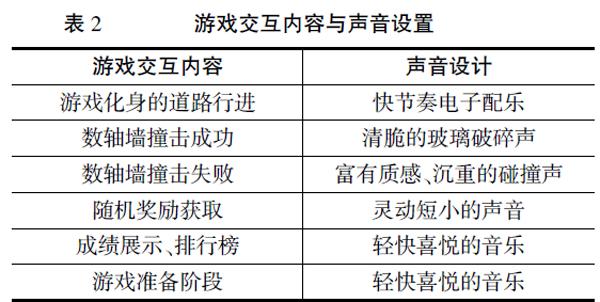
聲音是多媒體傳遞信息、創(chuàng)造良好視聽體驗的重要元素。依據(jù)梅耶的多媒體認知理論，記憶由語言系統(tǒng)和視覺系統(tǒng)構(gòu)成，記憶可以通過視覺編碼和言語編碼的聯(lián)結(jié)實現(xiàn)強化，同時呈現(xiàn)視覺信息和言語信息有助于促進記憶。本研究決定對聲音與游戲交互進行融合設計。具體聲音與游戲交互的搭配設計，見表2。比較典型的聲音設計是數(shù)軸墻的撞擊聲音，為了激發(fā)學習者的成就感，當游戲化身成功撞擊數(shù)軸墻，游戲會出現(xiàn)響亮、清脆的玻璃破碎聲。

五、游戲的應用效果

為檢驗分數(shù)游戲的應用成效，筆者在北京市順義區(qū)的一所公立小學開展了為期一周的準實驗研究，具體情況如下：

（一）研究方法與過程

本研究采用準實驗方法，四年級的兩個班共65名學生參加。參與學生每天在學校機房玩20分鐘《分數(shù)跑跑跑》，玩五天，共100分鐘。在實驗周期的設計方面，基于分數(shù)游戲的教育目的，在連續(xù)一周的五天內(nèi)進行游戲干預，與游戲的內(nèi)容模塊設計相匹配。

（二）研究工具

游戲化分數(shù)學習的應用效果測量包含兩個維度，其一是圍繞認知效果的分數(shù)概念性知識水平測試，其二是檢驗主體性體驗的動機等問卷量表。為測量學生的分數(shù)概念性知識水平，參考國外相關(guān)研究的測評方法，本研究的測試題目主要來自三大權(quán)威題庫，包括美國國家教育進展測評、國際數(shù)學與科學趨勢評估、美國加州標準測試。試題共有47道，每題1分，共47分。其中，第一類題目考察的知識是“分數(shù)與圖形”，共15道題;第二類題目考察的知識是“分數(shù)與數(shù)軸”，共15道;第三類題目考察的知識是“分數(shù)比較大小”，共17道。前測、后測所用題目相同。題目類型主要包括選擇題和填空題，代表性測試題目如圖2所示。

為全面考察分數(shù)游戲的應用效果，本研究使用相關(guān)量表以考察主體性體驗，包括內(nèi)在數(shù)學焦慮量表（The Modified Abbreviated Math Anxiety Scale）和動機量表（Intrinsic Motivation Inventory）。數(shù)學焦慮量表修正版是數(shù)學焦慮量表（AMAS）的縮略版。原量表共9個題目，在對問卷進行信效度分析之后，保留包含“測評焦慮”和“學習焦慮”兩個維度的8個題目（Cronbach's alpha=0.868），采用5點李克特量表的自我報告方式。內(nèi)在動機量表旨在測量學習者的興趣（Interest）、勝任力感知（Perceived Competence）、努力程度（Effort）等主觀感受。原始量表共涉及7個維度，本研究選取了和游戲化學習關(guān)系密切的兩個維度，“勝任力感知”和“興趣”（Cronbach's alpha=0.893）。該問卷采用5點李克特量表自我報告的方式。本研究所用問卷見表3。

（三）應用研究結(jié)果

在認知效果方面，數(shù)據(jù)結(jié)果顯示，在游戲化分數(shù)學習干預之前，前測總成績均值為23.83，標準差為7.8;第一類題目的前測成績均值為11.65，標準差為2.48;第二類題目的前測成績均值為7.23，標準差為3.59;第三類題目的前測成績均值為5.70，標準差為3.62。在一周的游戲化分數(shù)學習干預之后，后測總成績均值為30.44，標準差為7.68;第一類題目的后測成績均值為12.45.標準差為2.36;第二類題目的后測成績均值為8.53，標準差為3.36;第三類題目的后測成績均值為9.46，標準差為4.03。配對樣本T檢驗結(jié)果顯示，后測總成績均值顯著高于前測[t（64）=9.593，p=0.00]，第一類題目的后測成績均值顯著高于前測[t（64）=3.793，p=0.00]，第二類題目的后測成績均值顯著高于前測[t（64）=3.323，p=0.001]，第三類題目的后測成績均值顯著高于前測[t（64）=8.86，p=0.00]。

在主體性體驗方面，數(shù)據(jù)結(jié)果顯示，在游戲化分數(shù)學習干預之前，數(shù)學焦慮量表的測評維度的前測均值為2.3，標準差為1.09;學習維度的前測均值為2.09，標準差為1.07;數(shù)學焦慮量表整體前測均值為2.19，標準差為0.99。在一周的游戲化分數(shù)學習干預之后，數(shù)學焦慮量表的測評維度的后測均值為2.29，標準差為0.95;學習維度的后測均值為2.05，標準差為0.81;數(shù)學焦慮量表整體后測均值為2.17，標準差為0.8。配對樣本T檢驗顯示，數(shù)學焦慮量表子維度及整體前后測的均值無顯著差異（p>0.05）。在游戲化分數(shù)學習干預之前，數(shù)學學習內(nèi)在動機量表的勝任維度的前測均值為4.02，標準差為0.72;興趣維度的前測均值為4.1，標準差為0.82;量表整體前測均值為4.05，標準差為0.67。在一周的游戲化分數(shù)學習干預之后，內(nèi)在動機量表的勝任維度的后測均值為3.89，標準差為0.82;興趣維度的后測均值為4.2，標準差為0.86;數(shù)學學習內(nèi)在動機量表整體后測均值為4.03，標準差為0.71。配對樣本T檢驗顯示，內(nèi)在動機量表子維度及整體前后測的均值無顯著差異（p>0.05）。

總體而言，《分數(shù)跑跑跑》能夠顯著提高四年級學生的分數(shù)概念性知識水平。學生在考察分數(shù)概念理解程度的“部分與整體”（第一類測試題目）與“測量解釋”（第二類、第三類測試題目）后測中都有良好的表現(xiàn)。但與此同時，為期一周的游戲化學習體驗未能顯著降低四年級學生的數(shù)學焦慮水平，未能顯著提升學習動機水平。

六、結(jié)論與討論

本研究針對游戲化學習研究領域的核心問題——如何設計科學、有效、有趣的教育游戲，圍繞基礎教育階段的分數(shù)認知，以學習科學的跨學科視角進行數(shù)學游戲《分數(shù)跑跑跑》的設計開發(fā)。由于教育游戲兼具教育目的和娛樂目的，教育目的是教育游戲的根本目標，“娛樂”以服務“教育”為核心宗旨，因此，教育游戲在認知內(nèi)容上的科學性直接決定了教育游戲的使用價值。在教育游戲的科學性設計方面，應當堅持“立足跨學科視角的認知支持”原則，依據(jù)學習科學領域的相關(guān)研究成果進行認知內(nèi)容的設計。在科學性的基礎上，教育游戲需要著眼于實際問題，秉承“著眼教學實踐的設計驅(qū)動”原則，以實踐需求作為設計導向，確保教育游戲能夠有效地應用于教育教學。在保障科學性和有效性的基礎上，教育游戲可以借助游戲元素，充分調(diào)動學習者情緒，運用“借助情緒調(diào)動的動機發(fā)展”原則進行趣味性的設計。科學性、有效性與趣味性的層級關(guān)系與設計原則如圖3所示。

在教育游戲的科學性方面，依據(jù)游戲化學習體驗框架，基于情境的認知體驗設計主要參考認知神經(jīng)科學、教育學、心理學在分數(shù)認知方面的研究成果，確定游戲的核心認知內(nèi)容為分數(shù)概念性知識的測量解釋，以數(shù)軸作為核心認知輔助工具，參考三重編碼模型和數(shù)字發(fā)展的整合理論，分別設計了游戲中的分數(shù)表征和知識模塊框架。與此同時，為了保證教育游戲應用的有效性，在內(nèi)容設計的過程中，統(tǒng)籌考慮國家課程標準要求、教材元素、學生水平進行內(nèi)容設計。趣味性主要涉及基于動機的主體性體驗，基于動機理論設計了游戲情境和交互方式，結(jié)合關(guān)于情緒的相關(guān)研究設計了兼顧“努力”和“幸運”的獎懲機制，并且圍繞游戲元素設計了不同的聲音效果。基于65名四年級學生的準實驗數(shù)據(jù)結(jié)果，可以發(fā)現(xiàn)《分數(shù)跑跑跑》能夠顯著提高四年級學生的分數(shù)概念性知識水平。

回顧教育游戲在過去幾十年間的發(fā)展歷程，不難發(fā)現(xiàn)，技術(shù)發(fā)展確實為教育創(chuàng)新帶來了前所未有的機遇。游戲技術(shù)成功實現(xiàn)了虛擬化的認知情境創(chuàng)建，為學習者提供了即時、有效的信息反饋，也讓寓教于樂的理念得到了更加廣泛的認可，虛擬現(xiàn)實等新興技術(shù)也似乎展示了未來游戲化學習的無限可能。然而，機遇與挑戰(zhàn)并存，雖然游戲化學習是當前的研究熱點之一，教育游戲研究者終究需要回答“如何設計科學、有效、有趣的教育游戲”這一問題。以學習科學的跨學科視角進行教育游戲的設計開發(fā)具有巨大優(yōu)勢。認知神經(jīng)科學、教育學、心理學等關(guān)于學習基礎機制的研究成果為教育游戲的認知內(nèi)容和游戲元素的設計提供了參考。通過技術(shù)設計的方式，架起溝通基礎研究與教學實踐的橋梁，為解決教學實踐中的實際問題提供優(yōu)質(zhì)的游戲化學習資源。

[參考文獻]

[1] LIAO C Y， CHANG W， CHAN T. The effects of participation， performance， and interest in a game-based writing environment[J]. Journal of computer-assisted learning， 2018， 34（3）： 211-222.

[2] 陳博殷，錢揚義，李言萍.游戲化學習的應用與研究述評——基于國內(nèi)外課堂中的“化學游戲化學習”[J].遠程教育雜志，2017，35（5）：93-104.

[3] 李秀晗，曲茜美.游戲化學習在兒童數(shù)字化閱讀中的設計研究[J].電化教育研究，2018，39（12）：116-122.

[4] 徐杰，楊文正，李美林，等.國際游戲化學習研究熱點透視及對我國的啟示與借鑒——基于Computers & Education （2013—2017）載文分析[J].遠程教育雜志，2018，36（6）：73-83.

[5] 張露，尚俊杰.基于學習體驗視角的游戲化學習理論研究[J].電化教育研究，2018，39（6）：11-20.

[6] BANDURA A. Social cognitive theory： an agentic perspective[J]. Annual review of psychology， 2001， 52（1）： 1-26.

[7] HECH S A. Toward an information-processing account of individual differences in fraction skills[J]. Journal of educational psychology， 1998， 90（3）： 545-559.

[8] HECHT S A， VAGI K J. Sources of group and individual differences in emerging fraction skills.[J]. Journal of educational psychology， 2010， 102（4）： 843-859.

[9] FUCHS L S， SCHUMACHER R F， STERBA S K， et al. Does working memory moderate the effects of fraction intervention？ An aptitude-treatment interaction.[J]. Journal of educational psychology， 2014， 106（2）： 499-514.

[10] BOOTH J L， SIEGLER R S. Developmental and individual differences in pure numerical estimation.[J]. Developmental psychology， 2006， 42（1）： 189-201.

[11] CHARALAMBOUS C Y， PITTA-PANTAZI D. Drawing on a theoretical model to study students' understandings of fractions[J]. Educational studies in mathematics， 2007， 64（3）： 293-316.

[12] 辛自強，張睆.兒童的分數(shù)概念理解的結(jié)構(gòu)及其測量[J].心理研究，2012，5（1）：13-20.

[13] 尚俊杰，張露.基于認知神經(jīng)科學的游戲化學習研究綜述[J].電化教育研究，2017（2）：104-111.

[14] JACOB S N， NIEDER A. Notation-independent representation of fractions in the human parietal cortex[J]. Journal of neuroscience， 2009， 29（14）： 4652-4657.

[15] LORTIE-FORGUES H， TIAN J， SIEGLER R S. Why is learning fraction and decimal arithmetic so difficult？[J]. Developmental review， 2015， 38： 201-221.

[16] SIEGLER R S， FAZIO L K， BAILEY D H， et al. Fractions： the new frontier for theories of numerical development[J]. Trends in cognitive sciences， 2013， 17（1）： 13-19.

[17] SIEGLER R S， THOMPSON C A， SCHNEIDER M. An integrated theory of whole number and fractions development[J]. Cognitive psychology， 2011， 62（4）： 273-296.

[18] ISCHEBECK A， SCHOCKE M， DELAZER M. The processing and representation of fractions within the brain an fMRI investigation[J]. NeuroImage， 2009， 47（1）： 403-413.

[19] MALONE T W， LEPPER M R. Making learning fun：a taxonomy of intrinsic motivations for learning[M]//SNOW R E， FARR M J. Authentic learning environments. London： Routledge， 1987：223-253.

[20] 柴亞軍.ARCS動機模型在課堂教學中的應用研究[J].中國教育技術(shù)裝備，2017（23）：6-8.

[21] ANTONENKO P D， VANGOG T， PAAS F. Implications of neuroimaging for educational research[M]//SPECTOR J M， MERRILL M D， ELEN J， et al. Handbook of research on educational communications and technology. New York： Springer， 2014：51-63.

[22] 周加仙.教育神經(jīng)科學與信息技術(shù)的跨學科整合研究——訪英國著名教育神經(jīng)科學家保羅·霍華德·瓊斯教授[J].開放教育研究，2016（6）：4-10.

[23] 李澄宇，楊天明，顧勇，等.腦認知的神經(jīng)基礎[J].中國科學院院刊，2016，31（7）：755-764.