(3+1)維Boussinesq方程的多怪波解

鄭彭丹，席小忠

(1.中南林業科技大學涉外學院，湖南 長沙 410211；2.宜春學院數學與計算機科學學院，江西 宜春 336000)

非線性可積方程的孤子解對于理解非線性可積方程所描述的傳輸特性和動力學機制具有重要意義。怪波解是一類有理函數形式的孤子解，它在空間的各個方向上都是局部的。近年來，高維非線性可積方程的怪波解越來越受到人們的關注[1-5]。

本文要研究的是如下(3+1)維Boussinesq方程[6]

utt+3(u2)xx+uxxxx-uxx-uyy-uzz=0

(1)

其中u=u(x,y,z,t)。它描述了重力波在水面上的傳播。Gai[6]得到了方程(1)的多孤子解，同時討論了孤子的傳播特性。Wu[7]等人Riemann函數討論了方程(1)的多周期波解。Xu[8]利用貝爾多項式得到了方程(1)的雙線性形式，雙線性B?cklund變換以及lump解。本文打算利用以下符號計算方法討論方程(1)的多怪波解。

1 基本概念與方法

最近扎其勞教授[9]提出了一個符號計算方法來求解非線性可積方程的多怪波解，該方法簡單直接有效。主要步驟如下：

首先將一個行波變換υ=x+κz-ωt代入下列非線性可積方程

Y(u,ux,uy,uz,ut,uxx,uyy,uzz,…)=0

(2)

其中κ和ω是實常數，此時方程(2)將變成一個關于υ和t的(1+1)維的非線性可積方程：

Y(u,uυ,uy,uυy,uυυ,…)=0

(3)

為了獲得方程(3)的多怪波解，我們做如下變換

(4)

將方程(4)代入方程(3)平衡最高階導數項和非線性項的系數可得m。假設I(υ,y)滿足如下式子

I(υ,y)=Fn+1(υ,y)+2νyPn(υ,y)+2μυQn(υ,y)+(μ2+ν2)Fn-1(υ,y)

(5)

其中

其中F0=1,F-1=P0=Q0=0。其他常數都是待定的實常數。將方程(4)和方程(5)代入方程(3)可得原方程的多怪波解。

2 主要結果

按照以上符號計算方法的步驟，我們將行波變換υ=x+κz-ωt代入原方程(1)中可得

(6)

其中u=u(υ,y)。假設方程(6)有如下形式的解

u(υ,y)=2?υ,υ[LogI(υ,y)]

(7)

將方程(7)代入方程(6)可得

(8)

為了獲得方程(1)的1-怪波解，我們做出如下假設

I(υ,y)=(υ-μ)2+?1(y-ν)2+?0

(9)

將方程(9)代入方程(8)可得

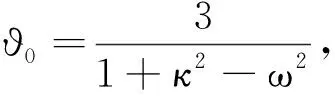
(10)

將方程(9)和(10)代入方程(7)，我們得到了方程(1)的1-怪波解

u(υ,y)=

(11)

怪波解(11)的動力學性質見圖1。

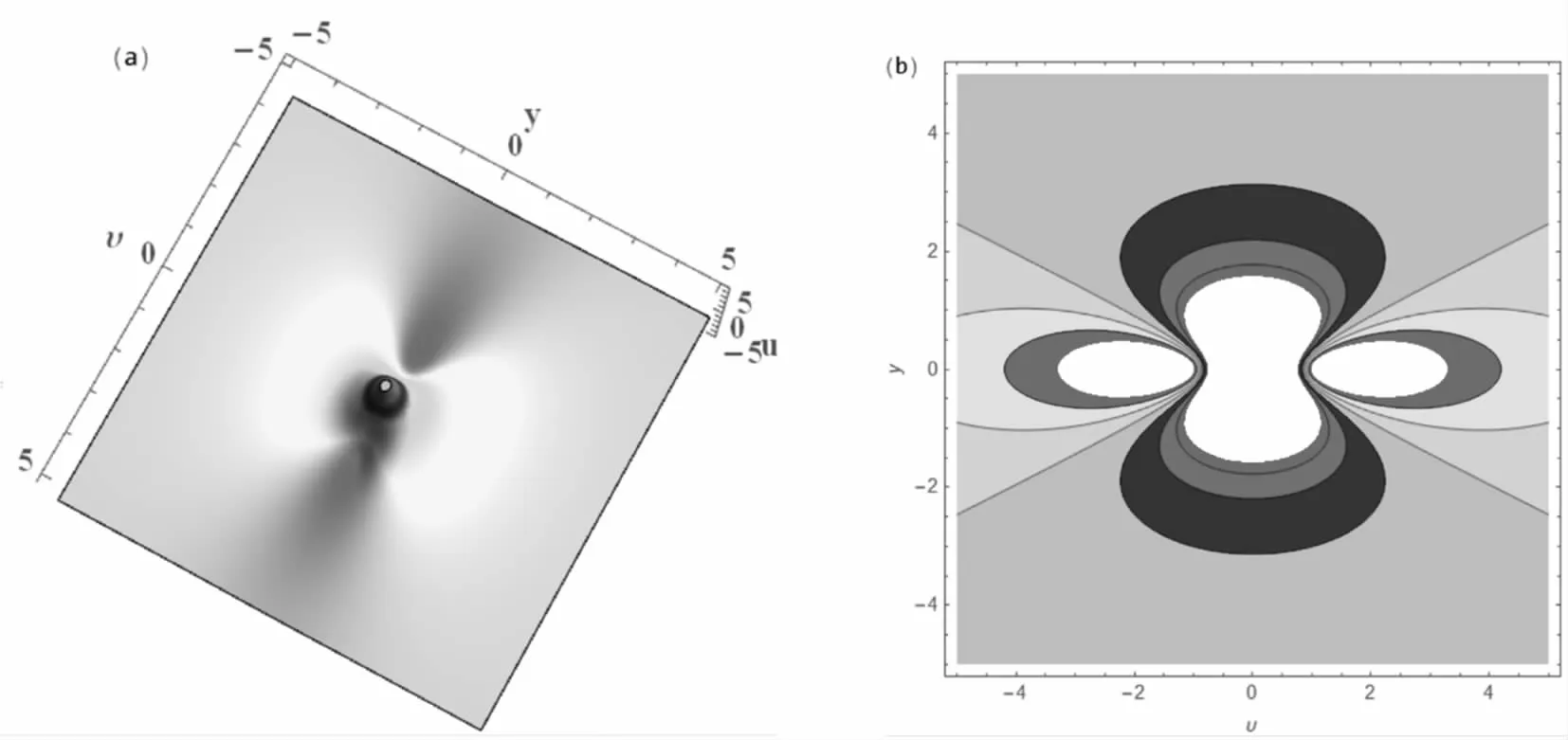
圖1 κ=-2,ω=1,μ=ν=0,(a) 三維圖形；(b) 等高線圖形

為了獲得方程(1)的3-怪波解，我們假設

I(υ,y)=υ6+?10υ4+?11υ4y2+(?12+?13y2+?14y4)υ2+?15y2+?16y4+?17y6+?18+2νy(?19+?20y2+?21υ2)+2μυ(?22+?23y2+?24υ2)+ν2+μ2

(12)

其中?i(i=10,11,…,24)、μ和ν都是實常數。將方程(12)代入方程(8)中，可得

?11=3(1+κ2-ω2),?14=3(1+κ2-ω2)2,?13=90,

(13)

其中?21和?24可以任意取值。將方程(12)和(13)代入方程(7)，我們得到了方程(1)的3-怪波解

(14)

I滿足條件(12)和(13)。怪波解(14)的動力學性質見圖2～圖4。

圖2 κ=-2,ω=?21=?24=1,μ=ν=0,(a) 三維圖形；(b) 等高線圖形

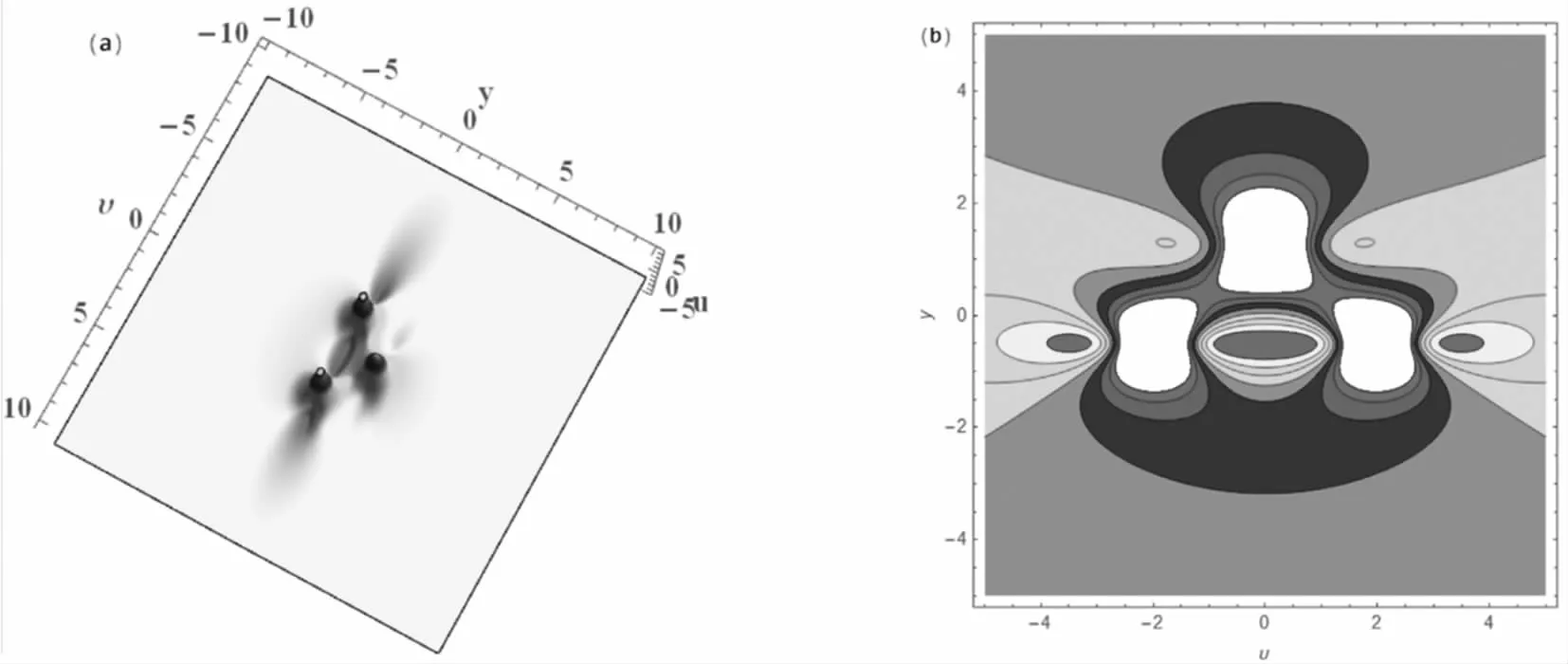
圖3 κ=-2,ω=?21=?24=1,μ=0,ν=100,(a) 三維圖形；(b) 等高線圖形

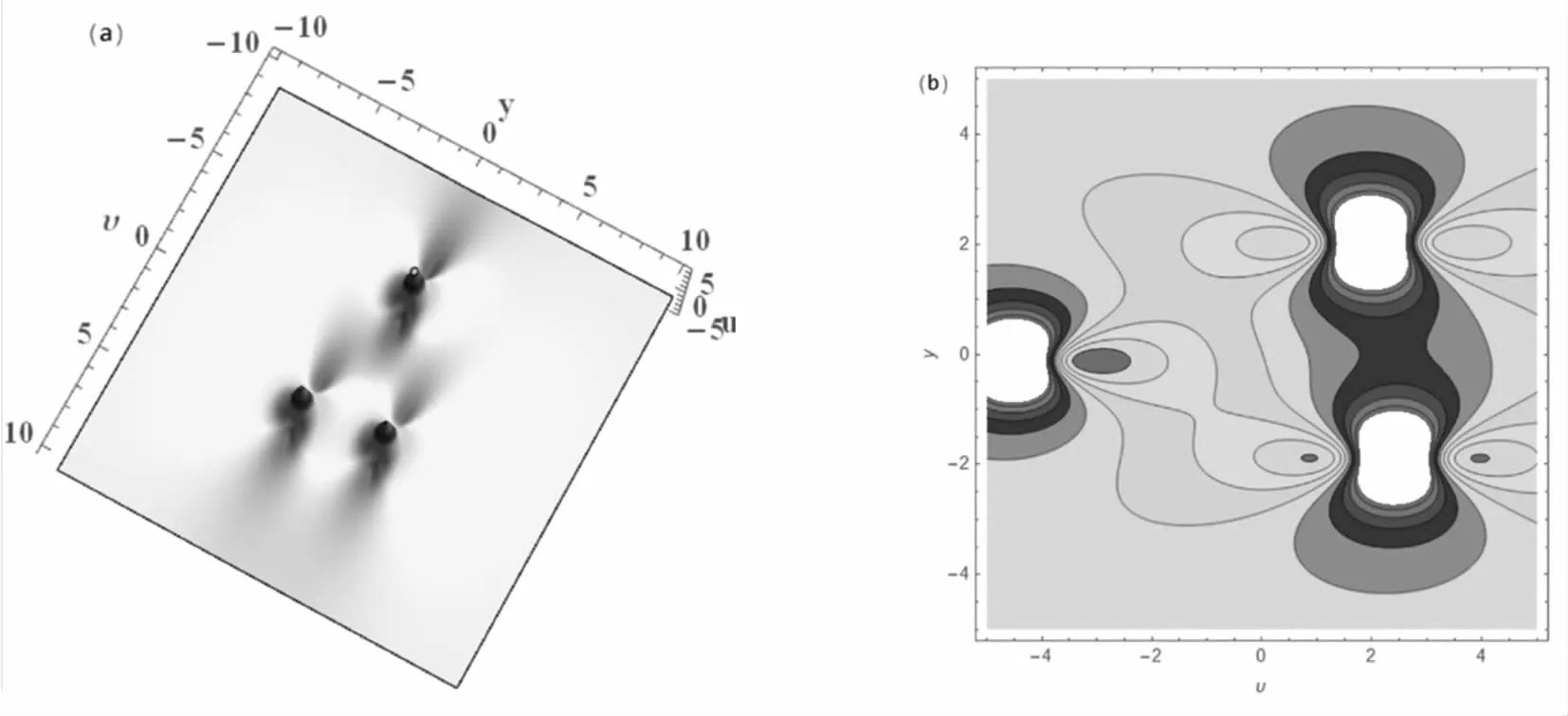
圖4 κ=-2,ω=?21=?24=1,μ=ν=100,(a) 三維圖形；(b) 等高線圖形

為了獲得方程(1)的6-怪波解，我們假設

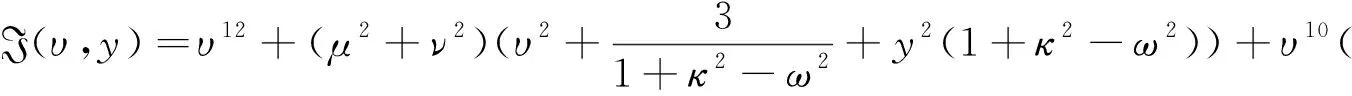
(15)

其中?i(i=25,26,…,69)是實常數。將方程(15)代入方程(8)中，可得

?26=6(1+κ2-ω2),?29=15(1+κ2-ω2)2,?28=690

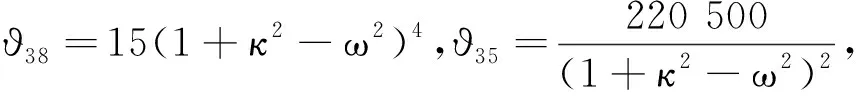
?50=(1+κ2-ω2)6,?49=58(1+κ2-ω2)4,?48=4335(1+κ2-ω2)2

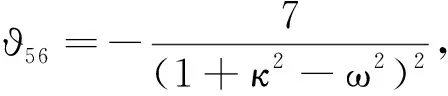
?69=-9(1+κ2-ω2),?65=

(16)

將方程(15)和(16)代入方程(7)，我們得到了方程(1)的6-怪波解

(17)

I滿足條件(15)和(16)。怪波解(17)的動力學性質見圖5。

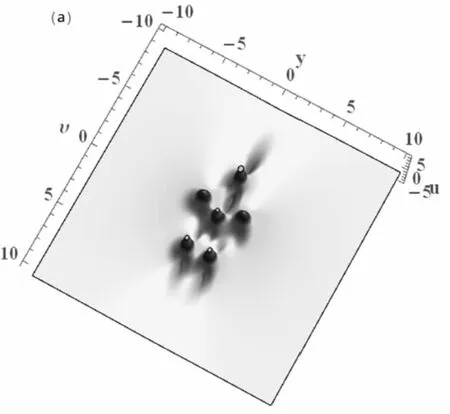
(a) 三維圖形

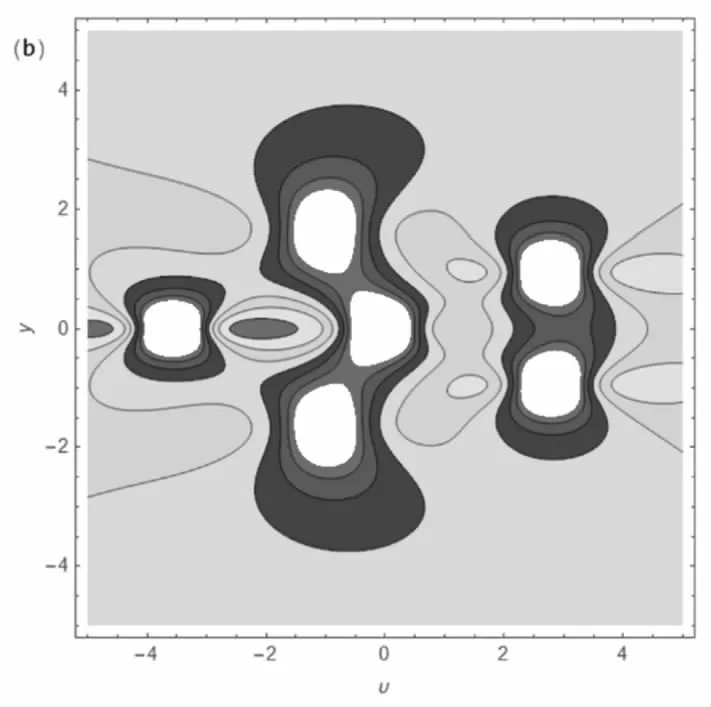
(b) 等高線圖形

3 總結

本文利用符號計算方法，獲得了(3+1)維Boussinesq方程的多怪波解，其中包括1-怪波解，3-怪波解和6-怪波解。通過選取參數不同的值，這些被獲得的怪波解的動力學性質被展示在圖1～圖5。