離散奇異隨機(jī)Markov跳變系統(tǒng)的N人Nash博弈
周海英
(廣州航海學(xué)院港口與航運(yùn)管理學(xué)院,廣州 510725)
1 引言與研究背景
現(xiàn)實(shí)實(shí)際中的許多系統(tǒng)在結(jié)構(gòu)和參數(shù)等方面往往都表現(xiàn)出隨機(jī)變化的規(guī)律,當(dāng)這種規(guī)律服從Markov過(guò)程時(shí),這樣的系統(tǒng)被稱為Markov跳變系統(tǒng)[1]。Krasovskii和Lidskii在1961年首次提出了Makov跳變系統(tǒng)的概念,隨后,Sworder基于隨機(jī)最大值原理討論了帶Makov跳變參數(shù)的混合線性系統(tǒng)并成功將其應(yīng)用到實(shí)際控制問(wèn)題。此后,Markov跳變系統(tǒng)因其在制造系統(tǒng)、飛行控制器系統(tǒng)、機(jī)器人操作系統(tǒng)、通信系統(tǒng)、神經(jīng)網(wǎng)絡(luò)中的分析仿真等方面都有著非常實(shí)際的應(yīng)用背景,引起了國(guó)內(nèi)外學(xué)者們的廣泛關(guān)注。近些年,Markov跳變系統(tǒng)逐漸成為研究熱點(diǎn),相應(yīng)的研究成果日益豐富[2-6]。一般地,僅由微分方程描述的系統(tǒng),稱為正常系統(tǒng);由微分代數(shù)方程(組)描述的系統(tǒng),稱為奇異系統(tǒng)。奇異系統(tǒng)相較正常系統(tǒng),更具廣泛適用性,其實(shí)際應(yīng)用背景豐富,如電網(wǎng)系統(tǒng),化工過(guò)程,核能源反應(yīng)堆以及社會(huì)經(jīng)濟(jì)領(lǐng)域等等。因此,學(xué)者們也越來(lái)越重視對(duì)奇異Markov跳變系統(tǒng)的分析以及研究。Tao等研究了時(shí)滯奇異隨機(jī)Markov跳變系統(tǒng)的容許性問(wèn)題[7],Chávez-Fuentes等探討了離散奇異Markov跳變系統(tǒng)的正則和穩(wěn)定性條件[8],Yu等探討了時(shí)變奇異馬爾可夫跳躍系統(tǒng)的觀測(cè)控制問(wèn)題[9],Zhang等探討了奇異Markov跳變系統(tǒng)的控制問(wèn)題[10]。
另一方面,微分博弈理論由于在經(jīng)濟(jì)、管理、自動(dòng)控制等領(lǐng)域應(yīng)用廣泛[11-13],備受關(guān)注。雖然確定性微分博弈向不確定隨機(jī)微分博弈的過(guò)渡是項(xiàng)艱巨的任務(wù),但卻是更符合客觀實(shí)際的。隨著時(shí)間的推進(jìn),微分博弈的相關(guān)研究已從一般系統(tǒng)擴(kuò)展到奇異隨機(jī)系統(tǒng)、Markov跳變系統(tǒng)等更為復(fù)雜的系統(tǒng)。
Moon等研究了馬爾可夫跳躍系統(tǒng)線性二次隨機(jī)零和微分博弈的充分條件[14]。Zhou等用配方法研究了連續(xù)時(shí)間和離散時(shí)間奇異隨機(jī)系統(tǒng)的線性二次微分博弈問(wèn)題,得到均衡策略存在的條件[15-16]。Mukaidani等給出了奇異隨機(jī)系統(tǒng)的Pareto策略及其數(shù)值求解算法[17]。Song等研究了Markov跳變系統(tǒng)二人零和微分博弈均衡策略[18]。Zhang等系統(tǒng)的研究了線性Markov跳變系統(tǒng)連續(xù)時(shí)間和離散時(shí)間下的Nash博弈均衡策略,并給出了其在金融保險(xiǎn)中的應(yīng)用[19]。Cao等研究了連續(xù)時(shí)間奇異隨機(jī)Markov跳變系統(tǒng)的Nash博弈問(wèn)題,給出了N人Nash均衡策略存在的條件及其顯式表達(dá)式[20]。縱觀上述文獻(xiàn),關(guān)于隨機(jī)奇異系統(tǒng)、Markov跳變系統(tǒng)微分博弈問(wèn)題已有一定成果,而關(guān)于奇異Markov跳變系統(tǒng)隨機(jī)微分博弈問(wèn)題的研究還處于起步階段。
基于此,本文對(duì)離散奇異隨機(jī)線性Markov跳變系統(tǒng)的N人Nash博弈問(wèn)題進(jìn)行分析,得到有限時(shí)間和無(wú)限時(shí)間下Nash均衡策略存在的條件及顯式表達(dá)式,并將所得結(jié)果應(yīng)用于隨機(jī)H2/H∞控制問(wèn)題。本文討論N人博弈問(wèn)題,相較于兩人博弈問(wèn)題,實(shí)際應(yīng)用范圍更廣且更具一般性;其次,討論的受控系統(tǒng)為離散奇異隨機(jī)Markov跳變系統(tǒng),充實(shí)了微分博弈的理論研究;最后,將所得結(jié)果應(yīng)用現(xiàn)代魯棒控制中的隨機(jī)H2/H∞控制問(wèn)題,豐富了微分博弈的應(yīng)用研究。
2 預(yù)備知識(shí)
考慮一類離散奇異隨機(jī)線性Markov跳變系統(tǒng):
{Ex(t+1)=A(rt)x(t)+C(rt)x(t)w(t),
x(0)=x0∈n
(1)
其中,x(t)∈n是狀態(tài)變量,w(t)是在給定的完備概率空間(Ω,F(xiàn),P)上的實(shí)隨機(jī)變量序列,且滿足ε(w(t))=0和ε(w(t)w(s))=δts,δts為克羅內(nèi)克算子。rt是一個(gè)取值于狀態(tài)空間Ξ={1,2,…l}的離散時(shí)間Marko過(guò)程,其轉(zhuǎn)移概率為Pr{rt+1=j/rt=i}=πij,轉(zhuǎn)移概率矩陣為Λ={πij}l×l,其中πij≥0且對(duì)于任意的i,j∈Ξ滿足和w(t)相互獨(dú)立。(x0,r0)∈n×Ξ是初始狀態(tài),E∈n×n是給定的奇異矩陣,rank(E)≤n,A(rt)、C(rt)為適維常數(shù)矩陣,當(dāng)rt=i(i∈Ξ)時(shí),A(rt)=A(i),C(rt)=C(i)。
為保證系統(tǒng)(1)解存在的唯一性,給出下述引理1。
引理1[21]對(duì)所有的i∈Ξ,如果存在一對(duì)非奇異矩陣U(i),V(i)使得對(duì)三元組式(E,A(i),C(i))滿足下述條件之一,則系統(tǒng)(1)存在唯一解。
(2)
其中A1(i),C1(i)∈r×r,C2(i)∈r×(n-r),C3(i)∈(n-r)×(n-r)。
其中Nn2(i)∈n2×n2是冪零的,且n1×n1,C2(i)∈n1×n2,n1+n2=n。
定義1[22]離散奇異隨機(jī)Markov跳變系統(tǒng)(1)是:
(Ⅰ) 正則的,如果對(duì)所有的i∈Ξ,det(sE-A)不恒為0;
(Ⅱ) 無(wú)脈沖的,如果對(duì)所有的i∈Ξ,deg(det(sE-A))=rank(E);
(Ⅲ) 均方穩(wěn)定的,如果對(duì)任意的初始條件(x0,r0)∈n×Ξ,都有
(Ⅳ) 均方容許的,如果它是正則,無(wú)脈沖和均方穩(wěn)定的。
引理2[21]離散奇異隨機(jī)Markov跳變系統(tǒng)(1)是均方容許的,如果存在矩陣P(i)=P′(i),使得對(duì)每一個(gè)i∈Ξ,下式成立:
E′P(i)E≥0,
(3)
3 有限時(shí)間N人Nash博弈
3.1 問(wèn)題描述
考慮以下離散奇異隨機(jī)線性Markov跳變系統(tǒng):
(4)
其中,x(t)∈n表示狀態(tài)變量,uk(t)表示博弈人k(k=1,2,…,N)的控制策略,其容許策略空間記為Uk。w(t)是實(shí)隨機(jī)變量序列,且滿足ε(w(t))=0和ε(w(t)w(s))=δts。rt是一個(gè)取值于狀態(tài)空間Ξ={1,2,…,l}的Markov過(guò)程,rt和w(t)相互獨(dú)立。當(dāng)rt=i,i∈Ξ時(shí),系數(shù)矩陣A(t,rt)=A(t,i),A1(t,rt)=A1(t,i),Bk(t,rt)=Bk(t,i)。
對(duì)于博弈人k,其性能指標(biāo)取經(jīng)典的線性二次型:
(5)
當(dāng)rt=i,i∈Ξ時(shí),Rk(t,rt)=Rk(t,i)≥0∈Snk,Qk(t,rt)=Qk(t,i)≥0∈Sn;當(dāng)rT=i時(shí),Mk(rT)=Mk(i)≥0∈Sn。
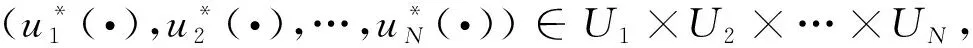
我們將研究限定博弈人的控制策略均為線性狀態(tài)反饋情形,即uk(t)=Kk(t,rt)x(t),其中Kk(t,rt)是適維矩陣。
3.2 主要結(jié)論
利用配方法,我們給出上述有限時(shí)間N人隨機(jī)Nash博弈問(wèn)題均衡策略的顯式表達(dá)和最優(yōu)性能指標(biāo)值。
定理1如果下述差分方程組(6)存在解Pk(t,rt)=Pk(t,i)∈Sn(i,j∈Ξ),
(6)
其中
則有限時(shí)間內(nèi),系統(tǒng)(4)-(5)的N人博弈問(wèn)題的Nash均衡策略集存在,其顯式表達(dá)式為
(7)
且最優(yōu)性能指標(biāo)值為
(8)
證明考慮任一博弈人k的最優(yōu)策略,其面臨的最優(yōu)化問(wèn)題為
s.t.Ex(t+1)=A-k(t,rt)x(t)+Bk(t,rt)uk(t)+A1(t,rt)x(t)w(t)
(9)
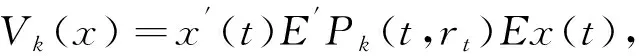
從而有:
(10)
(11)
對(duì)式(11)中的加和項(xiàng)進(jìn)行配方,得
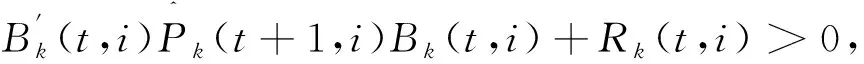
(12)
此時(shí),最優(yōu)控制策略和最優(yōu)性能指標(biāo)值如式(7)和(8)所示。
4 無(wú)限時(shí)間N人Nash博弈
4.1 預(yù)備知識(shí)
首先介紹無(wú)限時(shí)間隨機(jī)最優(yōu)控制中的一個(gè)重要概念——隨機(jī)穩(wěn)定性。
考慮如下離散奇異隨機(jī)Markov跳變系統(tǒng):
Ex(t+1)=A(rt)x(t)+B(rt)u(t)+A1(rt)x(t)w(t),t=1,2,…
(13)
其中,x(t)∈n是狀態(tài)變量,u(t)是容許控制過(guò)程,w(t)是實(shí)隨機(jī)變量序列,且滿足ε(w(t))=0和ε(w(t)w(s))=δts。
定義2[23]給定任意初始狀態(tài)x(0)=x0,r0=i,系統(tǒng)(13)是(均方意義下)隨機(jī)穩(wěn)定的,如果存在一個(gè)反饋控制u(t)=K(i)x(t)(i∈Ξ),其中K(i)均為常數(shù)矩陣,使得閉環(huán)系統(tǒng)Ex(t+1)=[A(rt)+B(rt)K(rt)]x(t)+A1(rt)x(t)w(t)是漸近均方穩(wěn)定的,即limt→∞ε[‖x(t)‖2]=0。
需要注意的是,與有限時(shí)間情形相比較,無(wú)限時(shí)間情形的不同之處表現(xiàn)為
(ⅰ) 系統(tǒng)(13)是時(shí)不變的且性能指標(biāo)中的權(quán)重矩陣為常數(shù);
(ⅱ) 當(dāng)T→∞時(shí),Mk(rT)=0;
(ⅲ) 要求系統(tǒng)(13)是均方穩(wěn)定的。
4.2 主要結(jié)論
考慮式(14)所示的奇異線性Markov跳變系統(tǒng):
(14)
其中,x(t)∈n是狀態(tài)變量,uk(t)是第k(k=1,2,…,N)個(gè)容許控制過(guò)程,表示博弈人k的控制策略,其容許策略空間記為Uk。w(t)是實(shí)隨機(jī)變量序列,且滿足ε(w(t))=0和ε(w(t)w(s))=δts。rt是取值于狀態(tài)空間Ξ={1,2,…,l}的Markov過(guò)程,rt和w(t)相互獨(dú)立。當(dāng)rt=i(i∈Ξ)時(shí),系數(shù)矩陣A(rt)=A(i),A1(rt)=A1(i),Bk(rt)=Bk(i)為適維常數(shù)矩陣。對(duì)于任一博弈人k,其性能指標(biāo)取經(jīng)典的線性二次型:
(15)
當(dāng)rt=i(i∈Ξ)時(shí),Rk(rt)=Rk(i)≥0∈Snk,Qk(rt)=Qk(i)≥0∈Sn。

∈U1×U2×…×UN,使下式成立:
同樣地,我們將研究限定博弈人的控制策略均為線性狀態(tài)反饋情形。
假定1[20]系統(tǒng)(14)是均方可穩(wěn)的。
利用配方法,得到無(wú)限時(shí)間離散隨機(jī)奇異Markov跳變系統(tǒng)N人Nash博弈問(wèn)題的均衡策略如定理2所示。
定理2在假定1成立的基礎(chǔ)上,若如下代數(shù)方程組(16)存在解Pk(rt)=Pk(i)∈Sn(i,j∈Ξ),
(16)
其中,
則無(wú)限時(shí)間內(nèi),系統(tǒng)(14)-(15)的N人博弈的Nash均衡策略集存在,其顯式表達(dá)式為
且最優(yōu)性能指標(biāo)值為
定理2的證明過(guò)程與定理1類似,此處不再贅述。
5 應(yīng)用于隨機(jī)H2/H∞控制
現(xiàn)代魯棒控制理論越來(lái)越廣泛應(yīng)用于工程實(shí)踐及社會(huì)科學(xué)領(lǐng)域,隨機(jī)H2/H∞控制獲得廣泛關(guān)注[17]。近年來(lái),將Nash博弈方法應(yīng)用于H2/H∞控制問(wèn)題,成為了一種有效的方法[24]。其基本思路是將控制策略設(shè)計(jì)者和隨機(jī)干擾性(不確定性)視為博弈的雙方,H2/H∞控制問(wèn)題就是控制策略設(shè)計(jì)者如何在預(yù)期到各種隨機(jī)干擾(不確定性)策略情況下設(shè)計(jì)自己的策略,在實(shí)現(xiàn)與隨機(jī)干擾性(不確定性)均衡的同時(shí)又使自己的目標(biāo)最優(yōu),這樣就可以把H2/H∞控制問(wèn)題轉(zhuǎn)化成Nash博弈問(wèn)題[24-25],利用Nash均衡策略得到相應(yīng)的魯棒控制策略。
本部分?jǐn)M將前文所得結(jié)果應(yīng)用于離散奇異Markov跳變系統(tǒng)的隨機(jī)H2/H∞控制問(wèn)題。為分析簡(jiǎn)單,本文僅探討有限時(shí)間情形,無(wú)限時(shí)間情形可類似分析。
考慮如下的受控系統(tǒng):
(17)
受控輸出:
式中,x(t)∈n是狀態(tài)變量,uk(t)是第k個(gè)容許控制過(guò)程,v(t)表示外界干擾。當(dāng)rt=i(i∈Ξ)時(shí),系數(shù)矩陣A(t,rt)=A(t,i),A1(t,rt)=A1(t,i),Q(t,rt)=Q(t,i)≥0,Bk(t,rt)=Bk(t,i),Qk(t,rt)=Qk(t,i)≥0。rt和w(t)相互獨(dú)立,v(t)和w(t)互不相關(guān),且初始值r0與w(t)相互獨(dú)立。其他符號(hào)含義如上文。L2(Ω,n)表示n值平方可和隨機(jī)向量空間。l2(NT,q)表示所有有限序列y(t)構(gòu)成的空間,其中y(t)∈L2(Ω,q)且對(duì)t∈NT是可測(cè)的,空間l2(NT,q)滿足
下面給出有限時(shí)間隨機(jī)H2/H∞控制的定義:
定義3[25]對(duì)于任意給定的γ>0,0 (ⅰ) ?v(t)≠0∈l2(NT,v),初始狀態(tài)x(0)=x0∈n的閉環(huán)系統(tǒng)(17)的狀態(tài)過(guò)程滿足: (ⅱ) 當(dāng)最壞干擾v*(t)∈l2(NT,v)存在時(shí),把v*(t)代入系統(tǒng),同時(shí)使性能泛函 ‖uk(t)‖2]達(dá)到最小。 引入表示干擾抑制水平的標(biāo)量γ>0,定義如下性能指標(biāo): 根據(jù)定理1,可得有限時(shí)間隨機(jī)H2/H∞控制的最優(yōu)策略以及最壞干擾的結(jié)果如定理3所示。 定理3對(duì)系統(tǒng)(17),如果下述差分方程組存在解Pk(t,rt)=Pk(t,i)∈Sn,P(t,i)∈Sn(i,j∈Ξ) 針對(duì)噪聲依賴于狀態(tài)與控制的離散奇異隨機(jī)Markov跳變系統(tǒng),分別討論其在有限時(shí)間和無(wú)限時(shí)間情形下的N人Nash博弈問(wèn)題,得到均衡解存在的條件及顯式表達(dá)式,并將所得結(jié)果應(yīng)用于相應(yīng)的H2/H∞控制問(wèn)題,得到了最優(yōu)策略存在的條件,充實(shí)了微分博弈理論和應(yīng)用研究。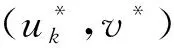
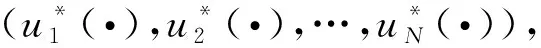

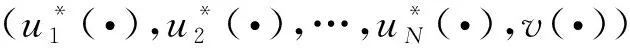

6 結(jié)論

