數形結合思想在初中數學教學中的應用探究

齊壽賢

摘 要：簡要分析了數形結合思想的作用，借助課例提出初中數學教學中應用數形結合思想的方法。

關鍵詞：數形結合;初中數學;應用探究

初中數學教學的目標和理念都在轉變，應新課程標準的要求，教師在教會學生知識的同時，也在積極地向他們滲透一些對學習有幫助的思想和方法，以達到“授之以漁”的效果。數形結合思想是學習數學最有力的工具之一，在教學中需要充分利用。

一、數形結合思想的作用分析

從初中數學教學的角度來說，數形結合思想的應用可以幫助學生解答有關幾何、代數、函數的問題，這也是初中階段最主要的知識點。數形結合通過將圖像與數字相結合，能夠將復雜的問題簡化，將抽象的問題直觀化，可用于問題的分析、解讀、題型歸類和解答[1]。此外，數形結合還可以用于一些問題的轉化、概念的解讀，只要充分發揮它的優勢和作用，才能有效提高學生學習數學的效率。

二、數形結合思想在初中數學教學中的應用

1.在有理數教學中的應用

有理數的知識內容中出現了“數軸”的概念，這便是數形結合的產物。在教學時教師一再向學生強調，每一個有理數都能在數軸上找到對應的點，這些點是數軸的構成，找到了有理數在數軸上的對應點就可以比較有理數的大小。此外，有理數的絕對值和相反數也可以在數軸中找到對應的位置。在教學這部分內容時，教師就要時刻向學生滲透數形結合的思想，讓他們明白，遇到與有理數相關的問題時，要通過畫數軸的方式來解決，這樣可以將許多問題瞬間變得直觀起來，答案不攻自破。

2.在應用題教學中的應用

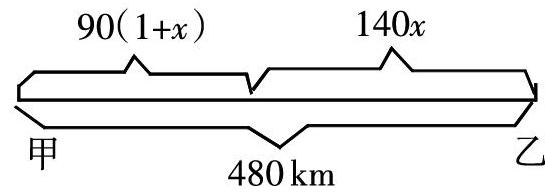
學生在應用題中出錯，有很大一部分原因是沒有理解題意或充分掌握數量關系，也或者是被題目中的干擾信息所誤導。每當遇到這種情況，學生只需要根據題目中的信息來繪制圖像，就能夠尋找到解題的突破口。如甲、乙兩站地之間的距離為480 km，一輛車現從甲站開出，以每小時90 km的速度行駛，另外一輛車從乙站開出，以每小時140 km的速度行駛。如果甲站的車開出1小時后乙站的車開出，兩車相向而行，乙站的車開出多久后兩車相遇？這個題目看起來十分復雜，給出的條件也較多，會給學生十分混亂的感覺，不知從何下手。這種典型的相遇問題完全可以通過畫圖來理清條件和數量關系，根據甲站開出的車所走路程與乙站開出的車所走路程總程為480 km的條件來繪制圖形（如下圖所示），設乙站開出的車行駛x小時后兩車相遇，就可列出“140x+90（x+1）=480”的方程式[2]。

只要學生掌握了數形結合的思想和應用方法，就能輕松解答某一類應用題，達到觸類旁通的效果。

3.在幾何教學中的應用

幾何部分的知識點在初中數學教材中占據了很大的篇幅，這部分內容更是有著圖形和數字相結合的特點，學生在學習以及解決問題時，時刻需要運用數形結合思想，否則將走很多彎路，學習難度很大。

比如，在比較兩個角的大小或者兩條線段的長短時，主要會運用到兩種方法，重疊比較法和幾何比較法。重疊比較法就是將兩條線段或兩個角重合，通過目測的方式即可比較出大小，是一種直觀和簡單的方法，但這種方法在考試中不具備利用價值。幾何比較法就是通過運用量角器、刻度尺等工具對線段、角進行測量后比較，是一種更加準確、科學的比較方法，也更具實用性，這就是數形結合最基本的應用。

4.在勾股定理教學中的應用

勾股定理是初中階段最重要的數學知識點之一，在解決各類問題時都有著廣泛的應用，教師需要在課堂中不斷重申這一知識點。在反復的強調中，可以從數形結合的角度去介紹勾股定理的用法，讓學生在數和形的巧妙結合中尋找一種解決數學問題的絕佳方法。在實際教學中，勾股定理在直角坐標系、代數等部分中都有應用，為了讓學生更好地掌握這個概念，教師應該將勾股定理的“形”用“數”進行表示，促進數與形融為一體。比如，一次函數圖象在直角坐標系中是一條直線，包括正比例函數與反比例函數，它們在直角坐標系中的圖象處于相反位置。二次函數在直角坐標系中的圖象是一條拋物線，其開口的方向、大小及所在區間取決于其對應的函數關系，這是教學中的一個難點所在，需要學生充分掌握數形結合的思想才能靈活運用該部分知識解決問題。在教學中，教師要多為學生總結“以形輔數”的解決方法，爭取讓學生在看到與勾股定理及函數相關的問題時，就能在腦海中構建起畫面，用作圖的方式迅速找到解決問題的方法。

參考文獻：

[1]白文娟.數形結合思想在初中數學教學中的應用與探究[J].中外交流，2019，26（28）：219.

[2]姜寶.數形結合思想在初中數學教學中的應用探究[J].考試周刊，2020（12）：76-77.