多輪分布式電驅動車輛雙重轉向分層控制系統設計*

陳路明，廖自力，張 征

（陸軍裝甲兵學院兵器與控制系，北京100072）

前言

輪式車輛一般依靠轉向機構進行轉向，在良好路面條件下具有較好的轉向性能［1］。履帶式車輛通常采用滑移轉向，這種轉向方式雖然存在履帶磨損嚴重、功率消耗大等缺陷，但在路面條件不佳時，滑移轉向是一種較為有效的轉向方式［2］。

為使車輛適應不同行駛工況，研究者設計了多種車輛動力學控制系統。其中，直接橫擺力矩控制（direct yaw-moment control，DYC）是一種應用較為廣泛的行駛控制技術［3］。DYC系統一般通過PID控制、最優控制、H∞控制和滑模控制（sliding mode control，SMC）等方法對車輛運動進行跟蹤，然后將力（力矩）需求分配至各個執行器［4-5］。分布式電驅動車輛通常裝配多個輪轂電機或輪邊電機，各個驅動電機相互獨立，可控性強、響應速度快，能夠實現驅動∕制動狀態間的快速切換，此外電機轉速、轉矩信息比較容易獲得，便于進行信息交互和信息融合，為車輛直接橫擺力矩控制帶來了獨特的優勢［6］。

與普通四輪驅動車輛相比，多輪車輛的行駛工況更加惡劣，通常需要在低附著路面、變附著路面甚至越野條件下保持機動，有時還要面臨緊急變道、小半徑轉向、高速轉彎等特殊工況，因此需要在道路識別基礎上，根據不同工況條件，對這類車輛進行有針對性地轉向控制［7-9］。

本文中根據多輪分布式電驅動車輛特點，將輪式車輛自然轉向與履帶式車輛滑移轉向相結合，設計了一種基于DYC的雙重轉向控制系統。在橫擺力矩決策層，根據擋位、加速踏板和轉向等輸入信號解析駕駛員意圖；將基于無跡卡爾曼濾波（unscented Kalman filter，UKF）和 最 小 二 乘 法（recursive least square，RLS）融合，對路面附著系數進行辨識；通過擬合車速因子和路面條件因子曲線對不同工況下的滑移轉向比進行自適應調節；設計了一種基于滑模條件積分（sliding mode control with conditional integrator，SMC&CI）算法的橫擺角速度控制器決策期望橫擺力矩。在驅動力分配控制層，按照分配規則將上層整車縱向力需求和期望橫擺力矩分配至各個執行器，實現車輛雙重轉向控制。最后，設計典型工況對控制策略進行了實時仿真驗證。

1 車輛動力學建模

1.1 車輛非線性動力學模型

以某型8×8輪轂電機驅動車輛為例，忽略空氣阻力，將滾動阻力線性化處理，建立非線性車輛模型［10］，如圖1所示。

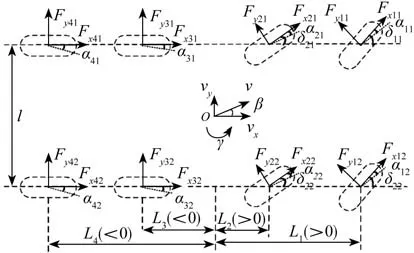
圖1 車輛非線性模型示意圖

車輛側向運動方程為

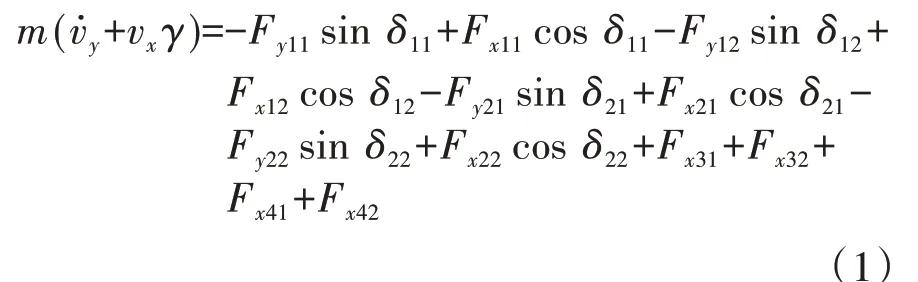
式中：m為整車質量；vx和vy分別為縱∕側向車速；Fx和Fy分別為輪胎縱∕側向力；i∈｛1，2，3，4｝表示車輛第i軸；j∈｛1，2｝表示左側和右側車輪；γ為橫擺角速度；δ為車輪轉角；l為輪距。

車輛橫擺運動方程為

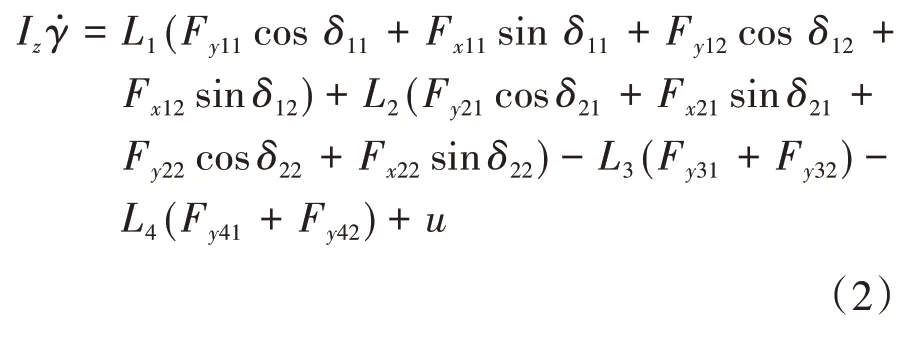
其中：

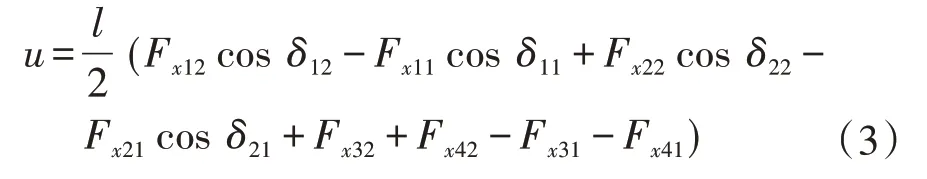
式中：Iz為橫擺轉動慣量；Li為車輛軸距；u為橫擺力矩。

輪胎側向力為

輪胎側偏角的近似計算公式為

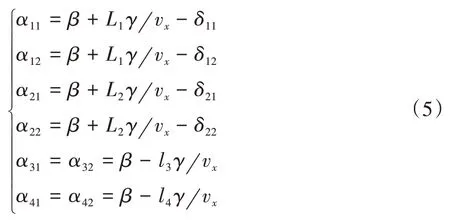
式中：Cα為輪胎側偏剛度；β為質心側偏角。

1.2 車輛雙重轉向參考模型設計

根據式（1）～式（5），建立車輛系統的狀態空間方程：

式中：x=［β γ］T為系統狀態向量；δ=［δ11δ12δ21δ22］T為轉向角向量。

系統狀態方程：

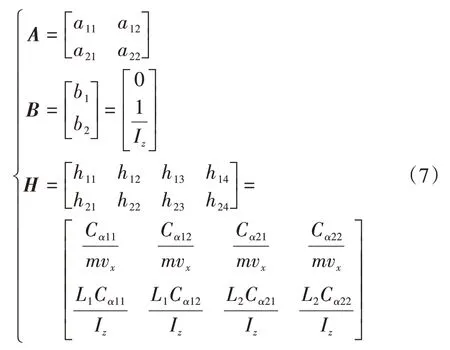
矩陣A中元素a11、a12、a21和a22的表達式分別為

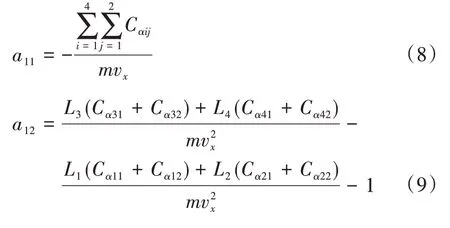
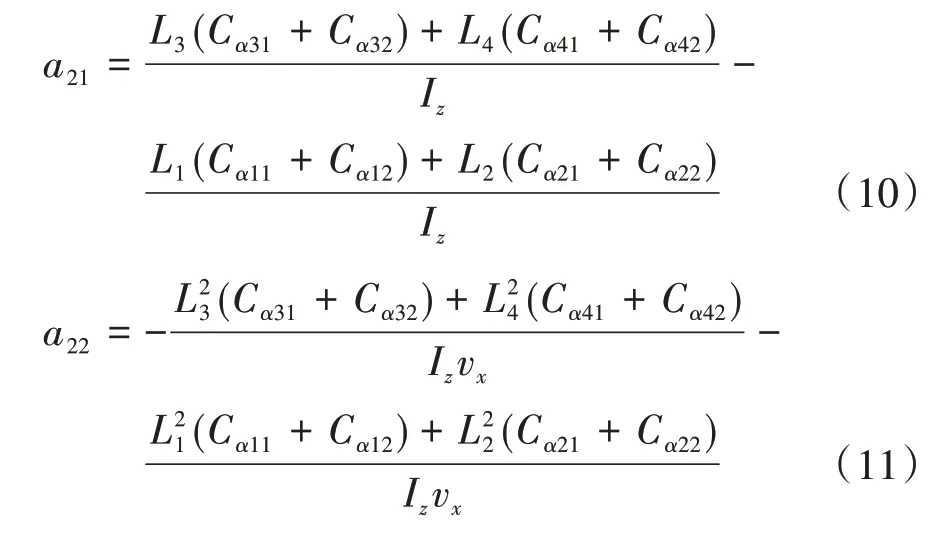
當車輛自然轉向時，參考橫擺角速度：

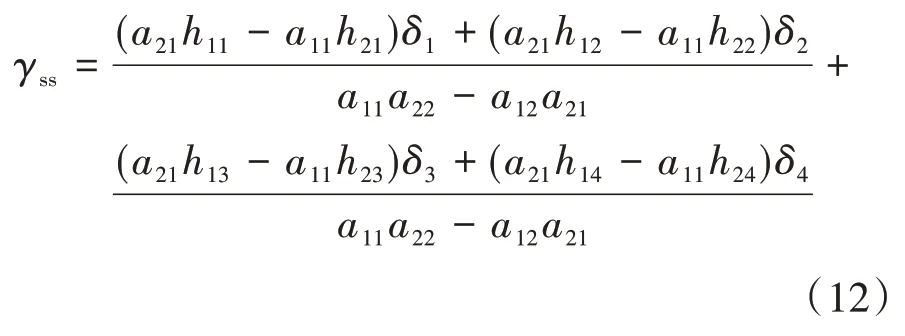
為滿足多輪輪轂電機驅動車輛機動靈活性需求，將輪式車輛自然轉向模式和履帶式車輛滑移轉向模式相結合，需修正γss。此外，車輛行駛時還需要考慮道路條件的約束，綜合這些因素，雙重轉向模式下的參考橫擺角速度為

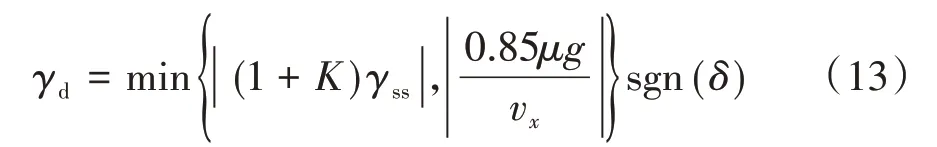
式中：sgn（δ）為轉向角的符號；比例系數K為滑移轉向比。

2 基于DYC的雙重轉向控制系統設計

2.1 控制目標和控制結構

具有雙重轉向功能的車輛旨在滿足4個主要控制要求：

（1）對行駛路面進行識別，根據行駛環境和駕駛員的意圖（如油門信號、轉向意圖等）做出適當的控制響應；

（2）當車輛在良好路面低速行駛時，若轉向靈活性需求較高，則增加雙重轉向中的滑移轉向比例，減小轉向半徑；

（3）當路面條件不佳或車速較高時，以轉向穩定性為主要控制目標，減小甚至消除滑移轉向比例；

（4）通過控制執行器實現系統動態平衡，將車輛行駛所需的廣義目標力合理地分配至各驅動輪。

基于上述分析，設計如圖2所示雙重轉向分層控制系統。

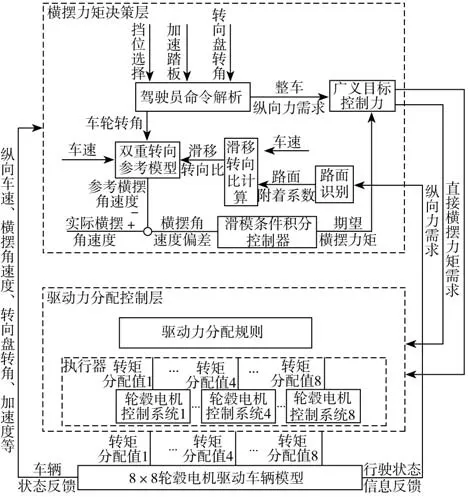
圖2 雙重轉向控制結構

2.2 路面識別算法設計

2.2.1 基于UKF算法的輪胎力估算

UKF算法通過非線性系統狀態模型對狀態參數進行估計，能夠消減模型線性化所產生的誤差［11］，本文中運用UKF算法對輪胎力進行估算。

建立參數估計方程

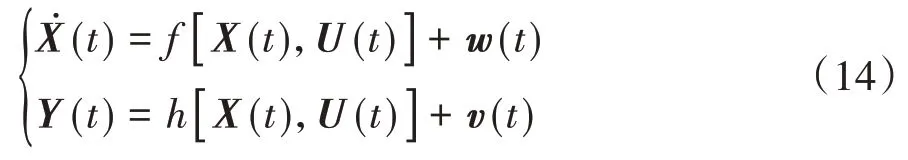
其中：狀態向量為

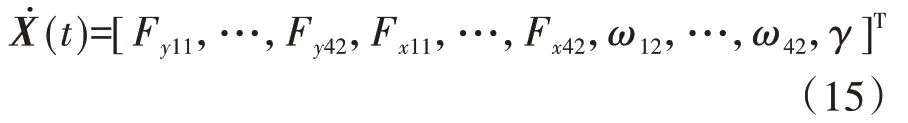
輸入向量為

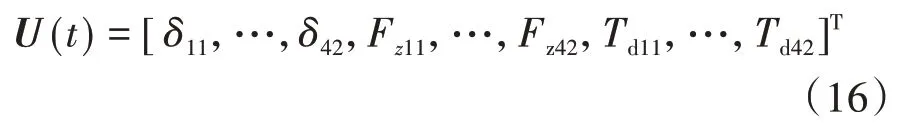
量測向量為

式中：I為車輪轉動慣量；ω為車輪輪速；Td為驅動力矩；ax和ay分別為縱∕側向加速度；w、v分別表示過程噪聲、量測噪聲。

設為X的均值，P為X的協方差，將X進行無跡轉換，創建2n+1個sigma點，有

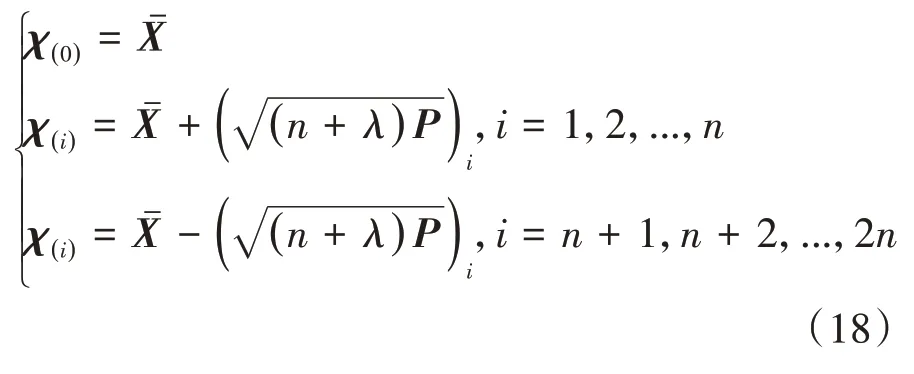
2n+1個sigma點權值為

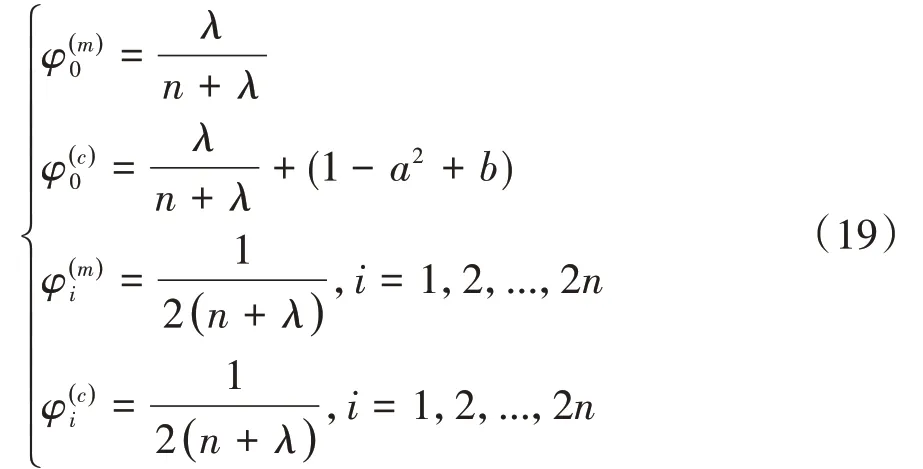
式中：、分別為X預測及更新的權值系數分別為P更新過程的權值系數；λ、a、b均為無跡變換參數。

狀態變量的初始條件設定，方程離散化處理，無跡變換和具體求解過程參見文獻［12］。

2.2.2 基于RLS的路面附著系數估計

Dugoff輪胎模型能夠描述車輛非線性特性［13］，將其作為路面識別的輪胎模型，表達式為

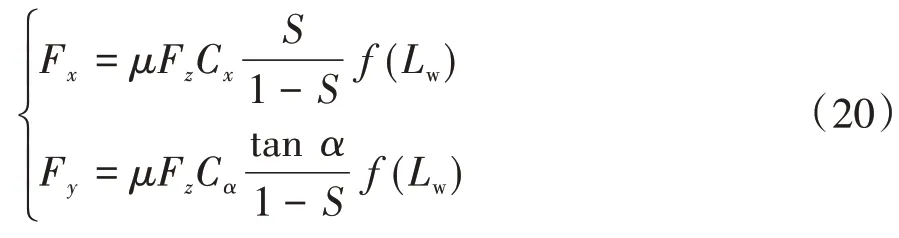
其中

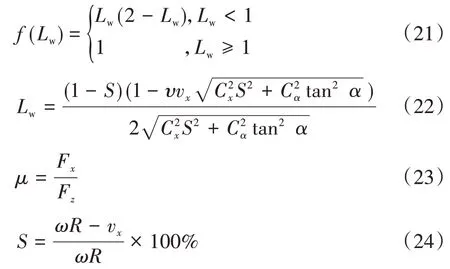
式中：Fz為輪胎垂向力；Cx為輪胎縱向剛度；Lw為非線性特征邊界值；υ為速度影響因子；S為車輪縱向滑轉率；μ為路面附著系數。

RLS估計量具備無偏、有效和相容等特點，基于Dugoff輪胎模型，運用RLS法進行μ的估算，具體步驟如下。

設z為根據UKF算法估算的輪胎力測量值。

將Dugoff輪胎模型表示為

式中：f[k，μ(k)]為Dugoff輪胎模型表達式；vl為隨機噪聲。

將z（k）線性化處理，其描述方程近似為

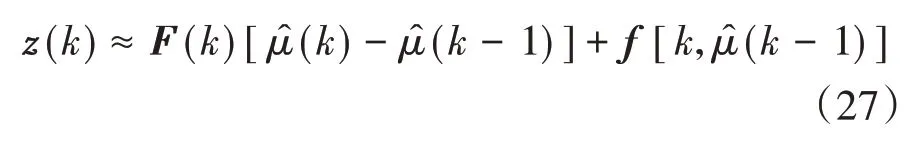
將h（k）定義為

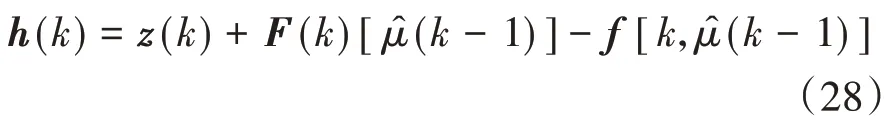
則

設RLS算法的價值函數為

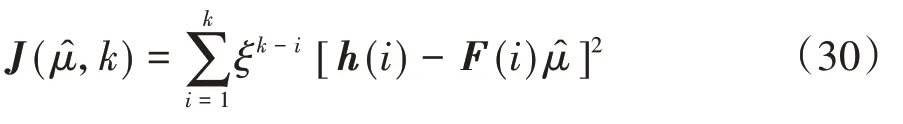
式中ξ為遺忘因子。

基于價值函數最小原則，得出RLS估算表達式，即

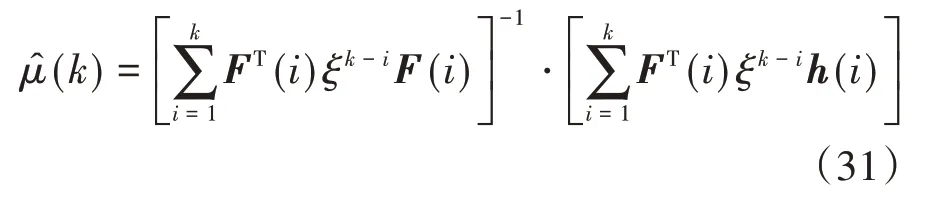
定義誤差協方差矩陣為

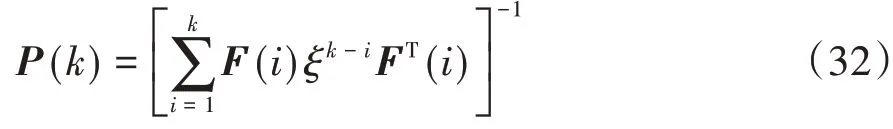
根據Sherman-Morrison方程進行遞歸計算：

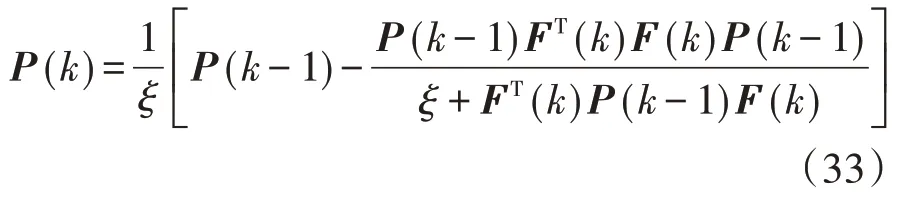
根據式（31）～式（33）進行迭代計算，具體迭代過程為

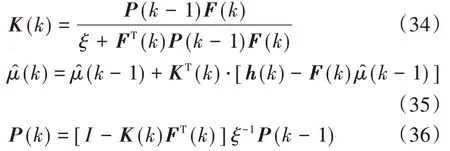
為減小估計誤差，迭代計算時設定滑轉率閾值Sup=8%，RLS估計僅在S＞Sup時迭代更新，當S≤Sup時，估計值按上一個時刻取值，即

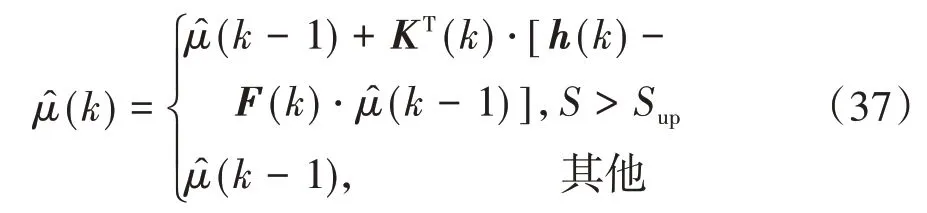
2.3 雙重轉向系統橫擺力矩決策層設計

2.3.1 滑移轉向比自適應調節

在不同路面和行駛狀態下，車輛行駛控制需求存在差異，多輪電驅動車輛雙重轉向控制系統需要根據行駛條件進行滑移轉向比K自適應調節。當道路條件良好且車輛速度較低時，適當增加滑移轉向比K能提高車輛在狹小環境下的轉向能力；當路面條件不佳，或車輛高速行駛時，應當以操縱穩定性為主要控制需求，減小K值甚至避免滑移轉向。根據上述分析，將車速和路面條件作為滑移轉向比例的兩個主要影響因素，利用基于多體動力學仿真數據和樣車實驗數據擬合車速因子σv和路面條件因子σμ曲線，如圖3和圖4所示。然后，根據σv和σμ得到不同行駛條件下的滑移轉向比K的映射，具體情況如圖5所示。

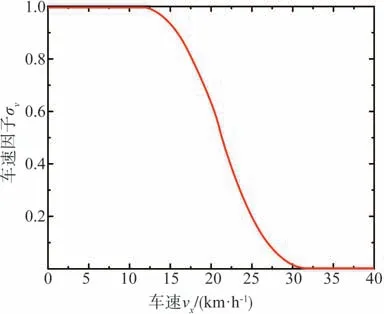
圖3 車速因子σv曲線

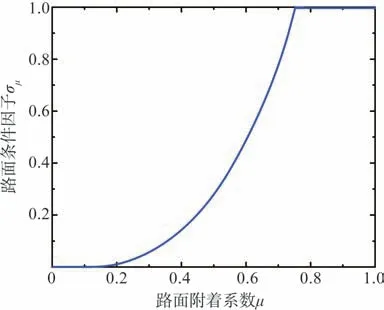
圖4 路面條件因子σμ曲線

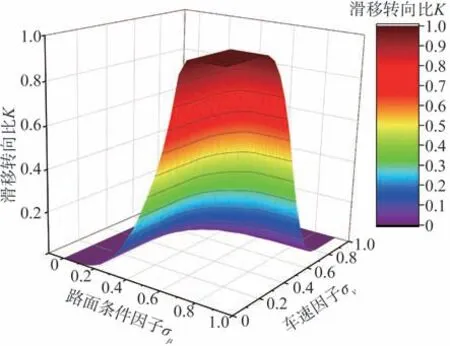
圖5 滑移轉向比K的映射圖

2.3.2基于SMC&CI的橫擺角速度控制器設計

SMC算法在車輛動力學控制中應用較為廣泛［14］。傳統SMC算法滑模面附近的非連續特性容易造成的控制信號抖動，因此，引入條件積分器對其進行改進，采用SMC&CI方法對車輛橫擺角速度進行調節，減小控制變量跟蹤誤差，并消減積分飽和現象。

車輛行駛時，控制變量跟蹤誤差為

設計控制器滑模面：

根據等速趨近律：

由式（39）和式（40）得

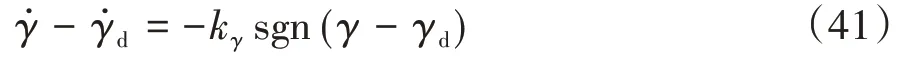
式中：kγ為等速趨近律參數，且kγ＞0；γd為期望橫擺角度。

結合車輛非線性動力學模型，計算出橫擺角速度滑模控制的期望橫擺力矩：

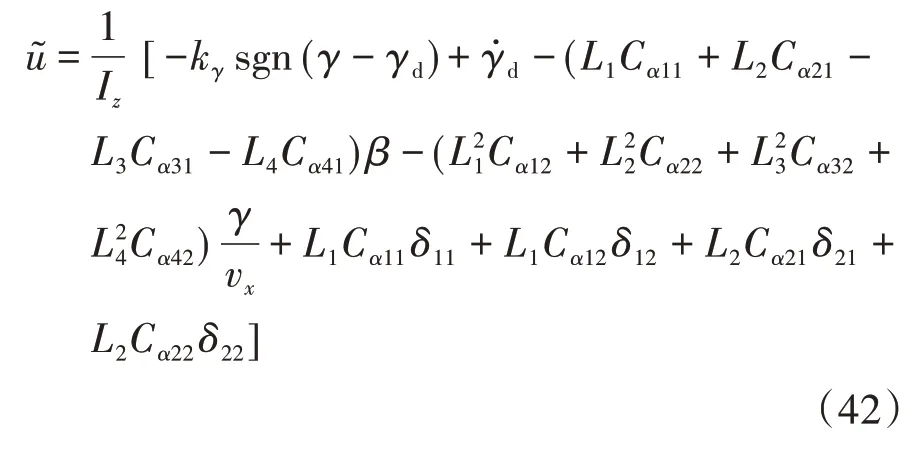
為盡量避免滑模面附近非連續特性造成的控制信號抖動現象，根據“積分分離”的思想，設計SMC&CI控制器對橫擺角速度進行控制。

在式（39）基礎上，增加條件積分

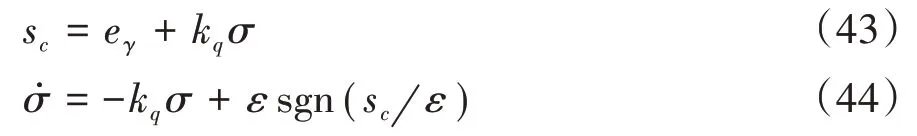
式中：sc（eγ，σ）=0為新增滑模面；σ為滑模條件積分誤差積分項，σ（0）≤ε∕kq；kq為誤差積分調節參數，kq＞0；ε為邊界層寬度，ε＞0。

為進一步減小控制系統抖動，將sgn（sc∕ε）換為飽和函數sat（sc∕ε），則有

由滑模條件積分控制器得出的期望橫擺力矩為

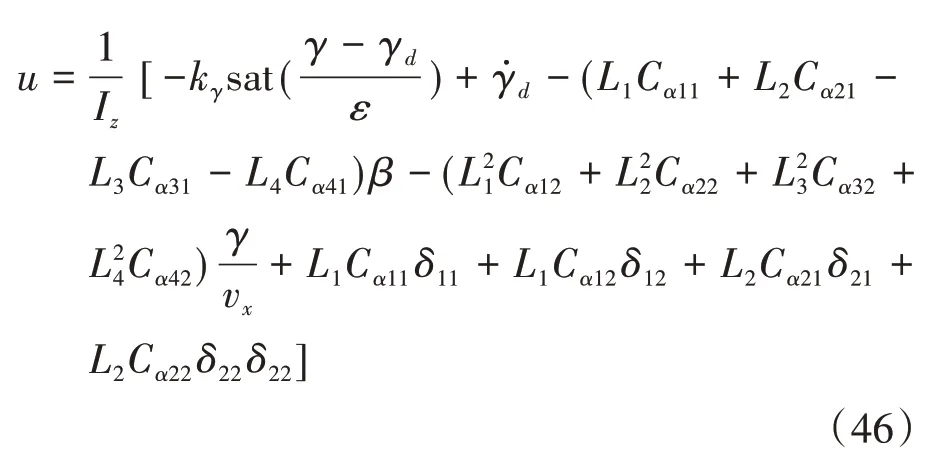
定義Lyapunov函數［15］為

則有

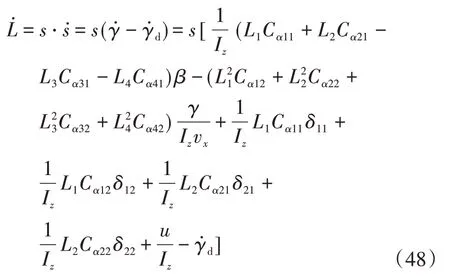
將式（46）代入式（48），可得L˙≤0，系統穩定性得證。

2.4 基于控制規則的驅動力分配層設計

DYC系統上層控制器確定的廣義目標控制力由分配在8個驅動輪上的驅動力產生，DYC系統下層需改變車輪兩側驅動力分配來實現雙重轉向模式，進行驅動力分配時需滿足：

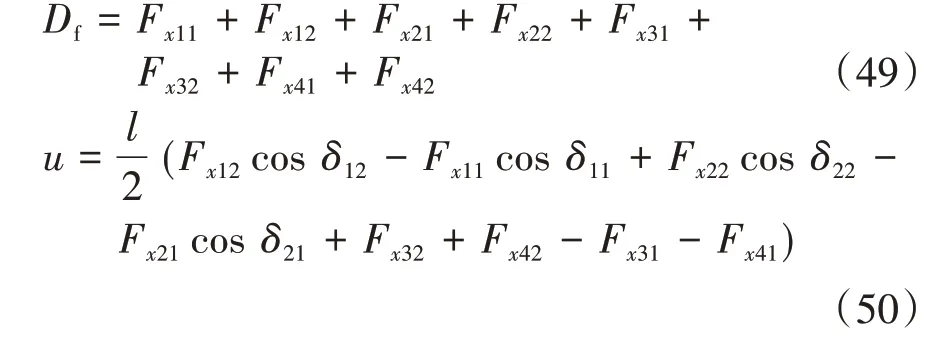
式中Df為駕駛員的驅動力需求。

采用同側驅動輪給定相同分配值，同軸驅動輪加減量互補原則設計驅動力分配規則，各輪分配結果為

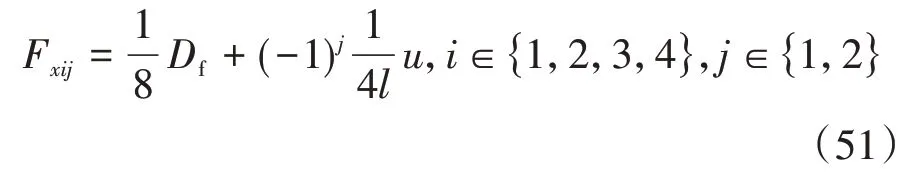
3 硬件在環實時仿真

采用圖6所示仿真平臺進行車輛雙重轉向控制策略實時仿真驗證，平臺包括：模擬駕駛艙、以實車中央控制器為核心的綜合控制系統、基于RT-LAB的電機驅動系統、基于RT-LAB的綜合電力系統和基于Vortex軟件的動力學仿真系統5個部分，各子系統間采用Flexray總線通信。

圖6 硬件在環實時仿真平臺

進行仿真時，將所設計的控制算法轉換為代碼，導入實車中央控制器，然后將中央控制器并入仿真系統，可模擬車輛實際運行環境。平臺間各子系統間信息交互如圖7所示。

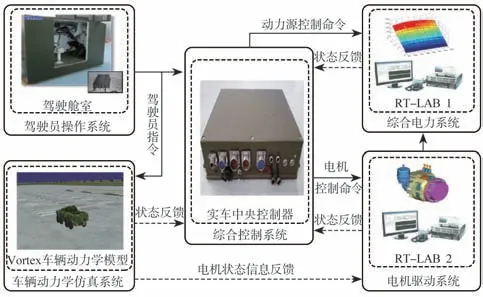
圖7 硬件在環實時仿真平臺

為了驗證所設計的分層系統在不同行駛工況下的控制效果，設計了表1所示3種典型工況，與無側向控制（轉矩平均分配）、滑模控制車輛（將γss作為參考橫擺角速度，車輛不具備雙重轉向功能）對比進行硬件在環仿真。

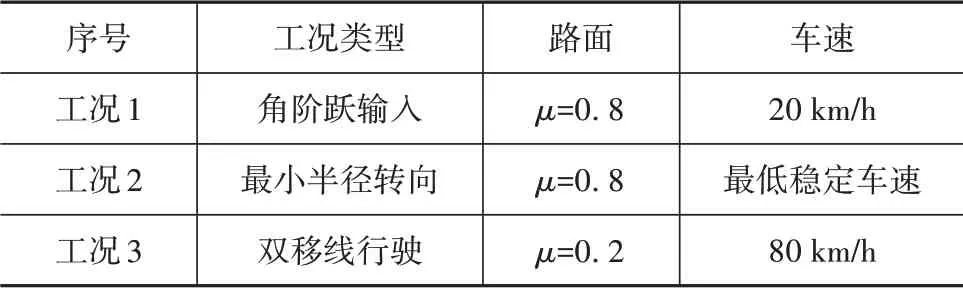
表1 仿真工況設置

仿真車輛采用的主要參數均根據實車數據給定，如表2所示。

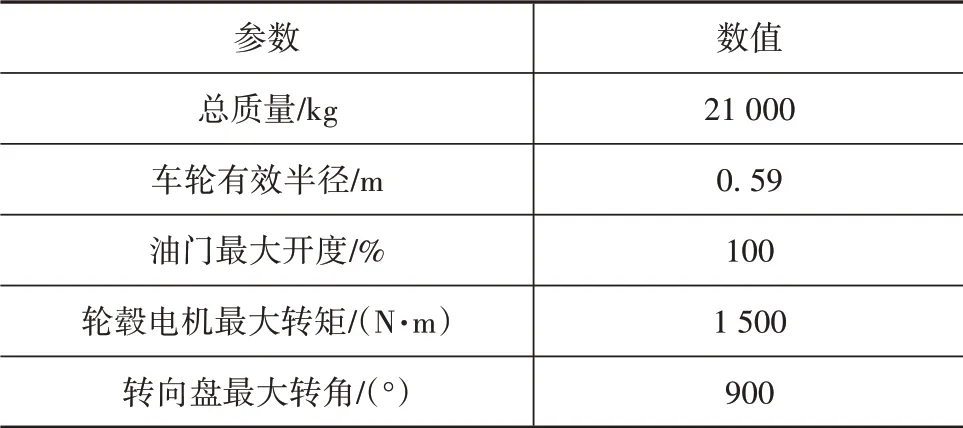
表2 車輛主要參數

3.1 角階躍輸入轉向工況

在t=2 s對車輛施加角階躍輸入轉向信號（如圖8所示），路面識別結果、橫擺角速度響應、轉向半徑及轉矩信息如圖9～圖12所示。

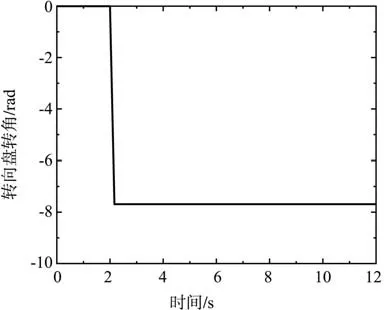
圖8 工況1轉向盤輸入信號

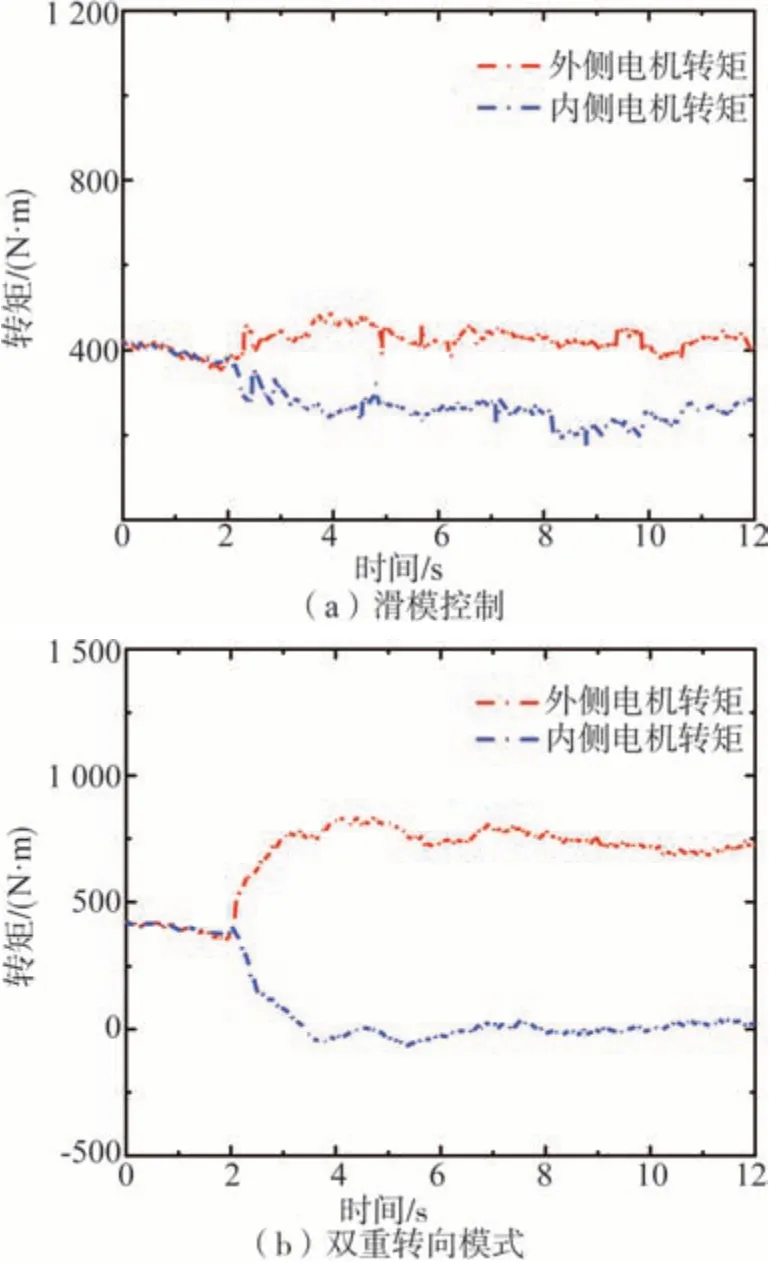
圖12 工況1輪轂電機轉矩

從圖9可以看出，在整個行駛工況中，基于UKF和RLS結合的路面識別算法準確地估算出了路面附著系數，估計值與實際值間平均誤差不超過10%。由圖10和圖11可知，對車輛施加角階躍輸入后，受到滑模控制和雙重轉向控制的車輛瞬態響應時間均縮短。在無控制、滑模控制和雙重轉向控制下，車輛穩態橫擺角速度均值分別為0.34、0.37和0.43 rad∕s。施加滑模控制的車輛穩態轉向半徑從無控制狀態下的25.1減為約22.6 m；采用雙重轉向控制后，穩態轉向半徑進一步減小，約為18.3 m。

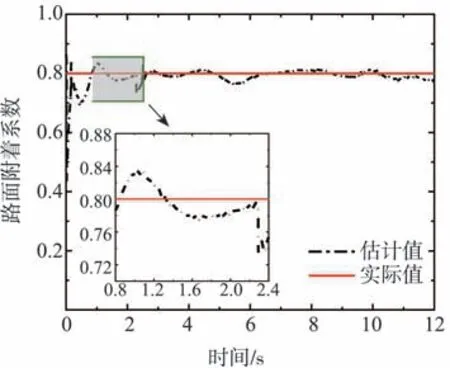
圖9 工況1路面附著系數估計

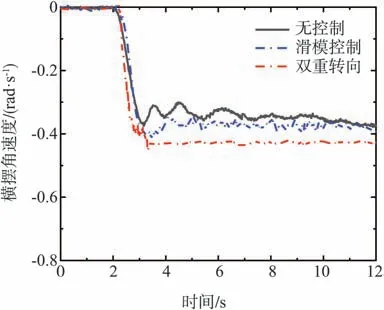
圖10 工況1橫擺角速度

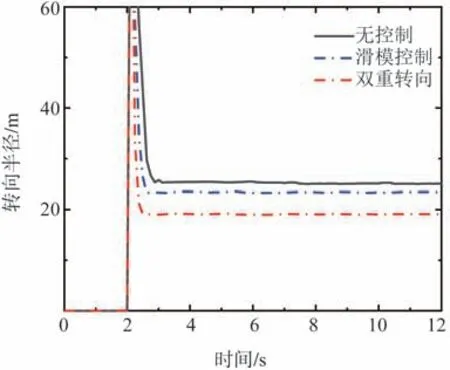
圖11 工況1轉向半徑

根據圖12可以看出，在滿足總轉矩需求的條件下，采用滑模控制和雙重轉向控制可以實現兩側輪轂電機轉矩值的差異分配，但是在轉向過程中，滑模控制下的車輛兩側電機轉矩輸出發生較明顯振蕩；而雙重轉向控制增加了左右側電機轉矩差，產生更大的直接橫擺力矩控制車輛運動狀態，通過對傳統滑模控制的改進，雙重轉向控制下車輛執行器轉矩輸出較為平穩，穩定性和魯棒性較好。

3.2 極限轉向工況

按照表1工況2設定的條件進行最小轉彎半徑仿真，轉向盤為滿程，結果如圖13～圖15所示。

由圖13可知，所設計的估計算法具有較好的路面識別效果，估計值與實際值間的偏差較小。從圖14和圖15可以看出，雙重轉向系統能夠根據車輛反饋狀態信息和路面信息對兩側電機轉矩進行調整，在高附著系數路面上，最小轉彎半徑約為8.3 m，無控制、滑模控制下車輛最小轉彎半徑分別為11.8和10.6 m。另外，與滑模控制車輛相比，施加雙重轉向控制后，電機轉矩整體變化趨勢較為平穩，波動較小，且兩側轉矩差更加明顯。仿真結果表明，雙重轉向控制下車輛的極限轉向性能明顯優于施加另外兩種控制的車輛。

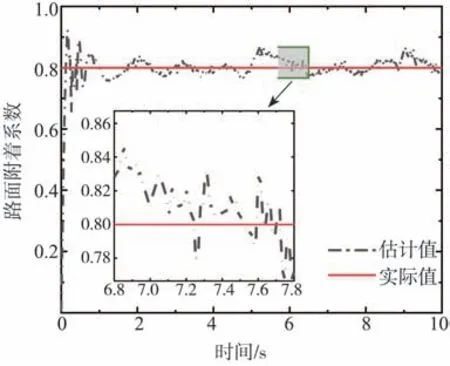
圖13 工況2路面附著系數估計

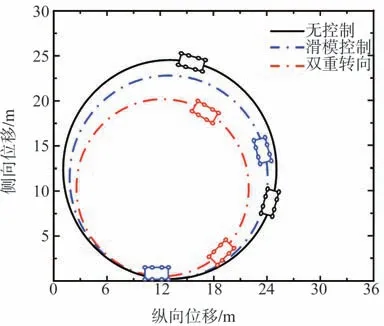
圖14 工況2轉向軌跡

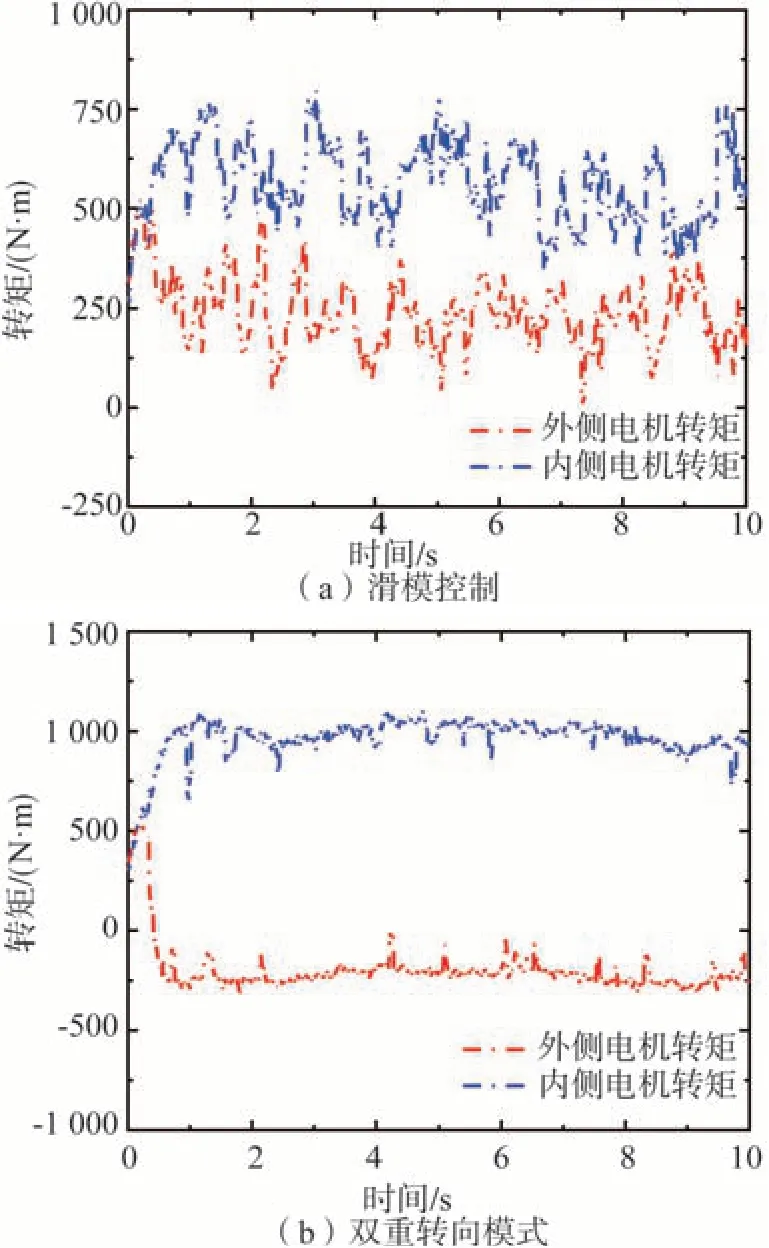
圖15 工況2雙重轉向模式電機轉矩

3.3 雙移線工況

按照表1工況3設定條件進行低附著路面雙移線仿真試驗，車輛行駛軌跡，狀態響應和電機轉矩等仿真結果分別如圖16～圖18所示。

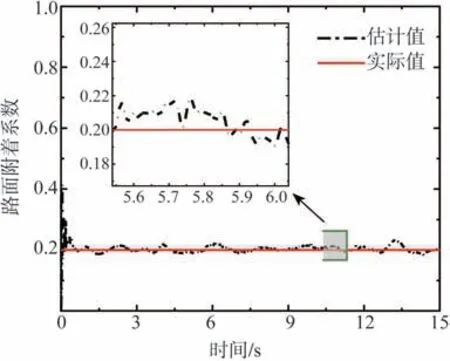
圖16 工況3路面附著系數估計

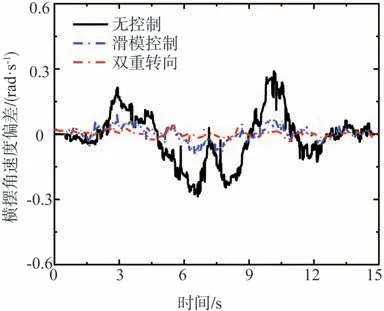
圖18 工況3橫擺角速度與參考值的偏差

由圖16可知，采用UKF和RLS融合算法對低附著系數路面辨識效果較好，估計值與實際值間的平均誤差較小，且波動平緩。從圖17～圖19仿真結果可以看出，受到道路條件限制，無控制車輛軌跡偏離較為明顯，行駛路徑與目標路徑偏差較大；施加滑模控制和雙重轉向控制的車輛均能較好地跟蹤期望路徑，雙重轉向控制下的路徑跟蹤效果最優。3種控制條件下車輛運動狀態響應差異較明顯，無控制車輛橫擺角速度偏差最大，車輛穩定性較差；采用滑模控制后，橫擺角速度與參考值的偏差明顯減小，但波動略大；具有雙重轉向控制系統車輛按照駕駛意圖和行駛狀態對電機轉矩進行了有效調節，車輛橫擺角速度偏差最小，且變化趨勢較平緩。由此可見，雙重轉向控制系統能夠在低附著路面、高速行駛工況下優先保證車輛的姿態保持能力和運動跟蹤能力，改善了行駛穩定性。

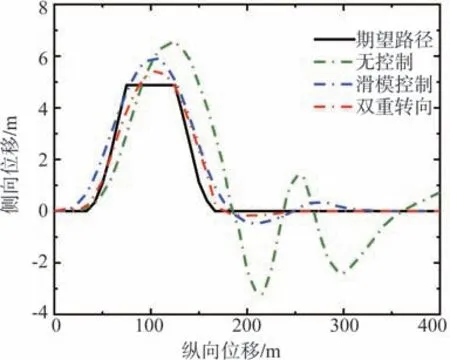
圖17 工況3車輛行駛軌跡

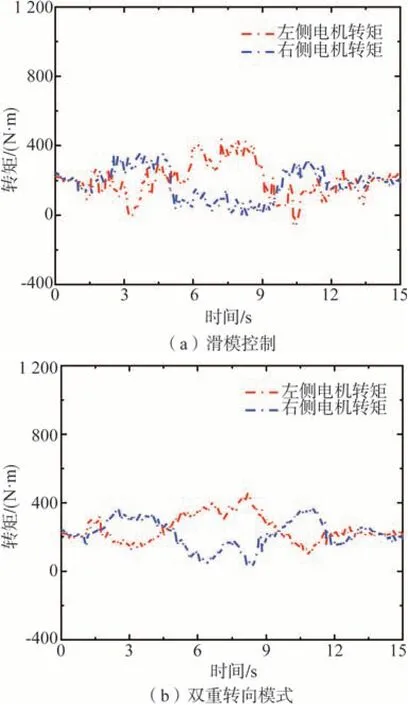
圖19 工況3雙重轉向模式電機轉矩

4 結論

根據多輪分布式電驅動車輛結構、動力源配置和操縱性等特點，提出了一種基于DYC的雙重轉向模式，建立了包括橫擺力矩決策層和驅動力分配層的分層控制體系。采用UKF和RLS結合算法估計路面附著系數，根據路面條件和行駛狀態計算滑移轉向比，得到了車輛雙重轉向參考模型。以此為基礎，設計了基于滑模條件積分算法的橫擺角速度控制器，建立驅動力分配模塊，實現了廣義目標控制力在執行器中的分配。硬件在環實時仿真結果表明雙重轉向控制系統能夠較為準確地辨識行駛路面，并針對不同路面條件和工況對車輛進行動力學控制，改善了車輛高附著系數路面小半徑轉向能力，最小轉彎半徑減小了3.5 m，提高了車輛低附著系數路面避障能力和操縱穩定性。