基于用戶大數據的電子助力制動器可靠性工況特征研究*

趙禮輝，周 馳，徐侃峰，王 震，鄭松林

（1.上海理工大學機械工程學院，上海200093；2.機械工業汽車強度與可靠性評價重點實驗室，上海200093；3.上海新能源汽車可靠性評價公共技術平臺，上海200093；4.上海匯眾汽車制造有限公司，上海200122）

前言

當前以電動化、智能化、網聯化為代表的新技術，推動著汽車產業的生態轉型［1］。電子助力制動系統能夠適應未來電氣化與自動化的發展需求，并適用于所有動力總成解決方案，成為當前制動系統的發展主流［2-3］。相對于傳統制動系統，電子助力制動系統響應速度的提升，使得助力器及制動系統相關部件沖擊載荷大幅提高，加劇了系統的潛在失效風險［4］。作為影響整車安全的核心部件，保障電子助力制動器的服役可靠性，是當前汽車行業共同面臨的關鍵技術問題之一（尤其在當前電動汽車大量制動事故的背景下）。

在汽車研發體系中，基于整車實際運行工況制定的臺架試驗是產品可靠性驗證的重要方式，相關的試驗載荷譜和失效模式及規律又是其可靠性設計的依據［5］。目前，針對電子助力制動器可靠性的試驗標準主要有AKB I∕II∕2016、GB 21670—2008、ISO 7635等行業采用較多的規范或標準，它們雖然有力地支持了助力器∕制動器的可靠性驗證及開發，但仍然存在試驗與用戶失效模式不一致、壽命差異大等情況。其主要原因是當前規范或標準體系大多采用較大制動強度對應的主缸壓強工況進行加速，載荷大、工況少、不同部件的考核強度不一致。雖然AKB—2016采用多達27級制動壓強進行制動系統可靠性驗證，但由于其總體目標僅以幾千公里的國外用戶制動數據外推而來，不僅用戶覆蓋水平有限，也難以反映中國用戶使用條件下的電子助力制動器工況特征。

如何準確地定義電子助力制動器全壽命周期可靠性目標，是其可靠性評價的前提。面對制動系統工況載荷與用戶駕駛行為的強相關性，傳統的基于“用戶調研-小樣本載荷采集-全壽命周期外推”可靠性目標及工況確定方法［6-8］，不能滿足電子助力器及制動器高可靠性的要求。主要體現在：（1）調研和經驗的工況定義難以全面反映用戶群體的要求；（2）小樣本的用戶道路載荷采集不足以覆蓋小概率的極端工況，導致制定的可靠性試驗規范與用戶實際差異較大。近年來，車聯網的快速發展使得車輛動態運行數據的大規模獲取成為現實，為構造制動系統可靠性相關的工況特征及目標構建提供了有力的支撐［9-10］。但目前尚缺乏較為通行的面向用戶大數據的電子助力制動器可靠性工況特征分析方法。

本文中以用戶的運行大數據為基礎，通過提取制動工況片段，對制動工況特征進行分析，結合臺架試驗數據，建立用戶運行數據與工況載荷之間的等效關系，并研究不同用戶制動工況損傷分布規律，從而提取用戶實際使用條件下的電子助力器工況及損傷特征，為構建電子助力制動器高用戶百分位可靠性目標奠定基礎。

1 用戶制動工況提取

1.1 總體技術路線

本文中以用戶車輛運行數據為基礎，對電子助力制動器可靠性工況特征進行研究，具體流程如圖1所示。

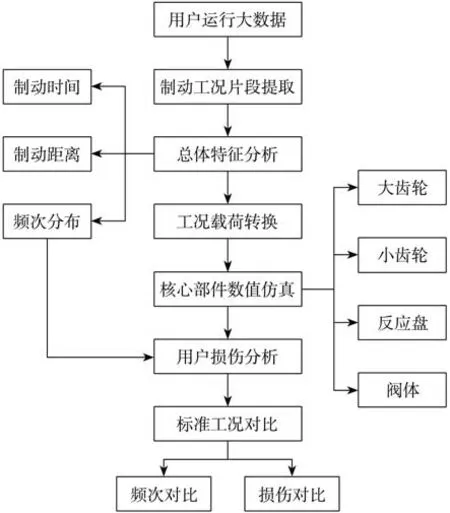
圖1 電子助力制動器可靠性工況分析流程

1.2 用戶大數據

本文中采用的用戶數據涵蓋華中、華北、華東、華南、西北5個地區，共300個用戶1年的運行數據，采樣頻率為10 Hz。剔除采集過程中由于信號不良等導致的異常數據，生成新的載荷數據。總時長為135 440 h，總行駛里程為3 547 640 km，其中部分城市用戶行駛軌跡如圖2所示。

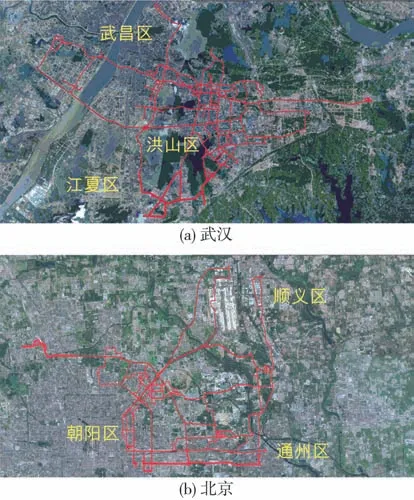
圖2 部分用戶行駛軌跡

1.3 制動工況片段提取

由于車輛運行過程中存在勻速狀態引起較小的速度波動情況，為準確獲取制動工況特征，在提取制動工況片段時定義劃分準則，如表1所示。

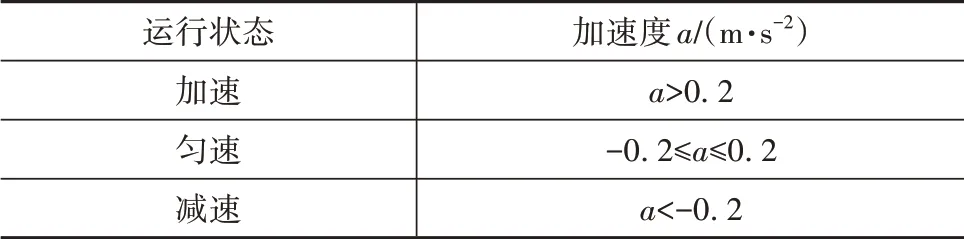
表1 運行狀態劃分準則

從用戶運行數據中選一段速度時間序列進行制動工況片段的提取，如圖3所示。其中，加速段為速度持續增加的過程；勻速段為速度在小波動范圍內保持不變的過程；減速段為速度持續減小的過程。基于用戶運行數據，最終提取出制動工況片段共計32 741 454個。

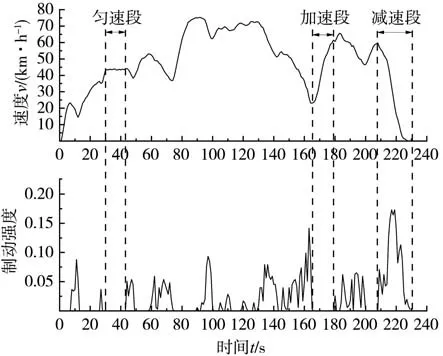
圖3 制動片段提取示意圖

2 制動工況特征分析

用戶實際使用條件下制動工況存在差異，采用合適的分布模型可以有效地分析各用戶之間的整體特征。本文中采用擬合優度檢驗方法，結合常用的正態、對數正態、威布爾、3參數對數logistic等分布模型，以最小二乘法對分布進行參數估計，通過AD（anderson-darling）檢驗統計量確定最優分布模型，AD檢驗統計量［11］為

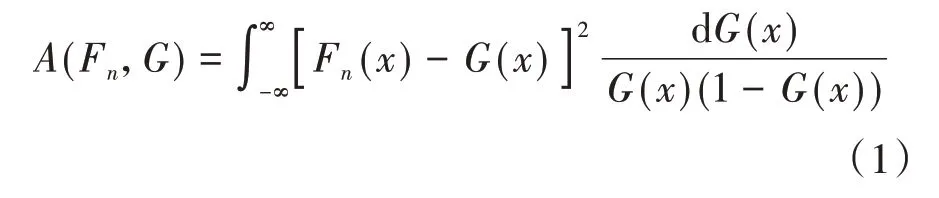
式中：Fn(x)為經驗分布函數；G(x)為樣本分布函數。

通過AD檢驗統計量，對比不同分布簇臨界值的大小，當A(Fn，G)大于臨界值時拒絕原假設H0，否則在顯著度水平α下接受假設H0。其中，若AD檢驗統計量越小，則說明該分布擬合效果越好，數據越服從目標函數分布。

2.1 制動時間和里程總體分析

根據提取的制動工況片段，得到制動工況總時間為36 742 h，總里程為1 207 323 km。基于用戶數據提取出的制動工況總時間與總里程，得到制動工況總時間與總里程占比分別為27%和34%。

2.2 單次制動時間分析

根據提取的制動工況片段，統計每個片段制動工況的持續時間，對制動工況時間數據進行分布擬合。單次制動時間服從對數正態分布模型，其概率分布和累積概率分布如圖4和圖5所示。

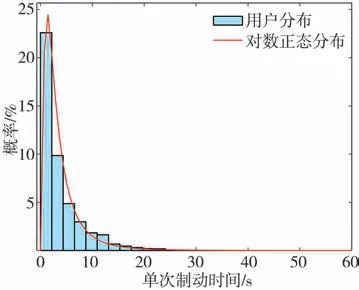
圖4 單次制動時間概率分布

從圖4中可得，總體單次制動時間在20 s以內。從圖5中可得，95%單次制動時間在11.56 s以內。

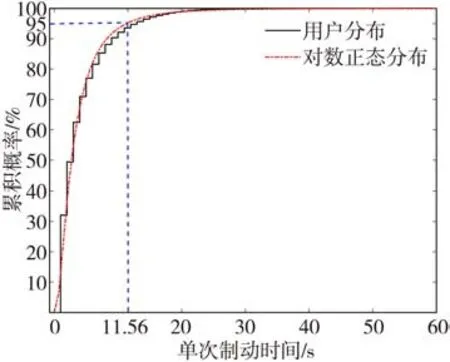
圖5 單次制動時間累積概率分布

2.3 單次制動距離分析

為分析用戶實際制動過程中制動距離分布的特征，提取所有制動工況片段的速度時間歷程，統計單次制動工況下的制動距離，對單次制動距離進行分布擬合。單次制動距離服從Weibull分布模型，其概率分布和累積概率分布如圖6和圖7所示。

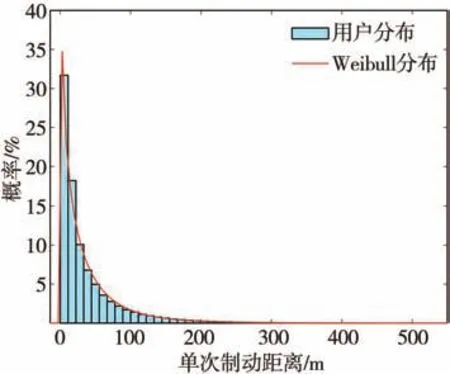
圖6 單次制動距離概率分布

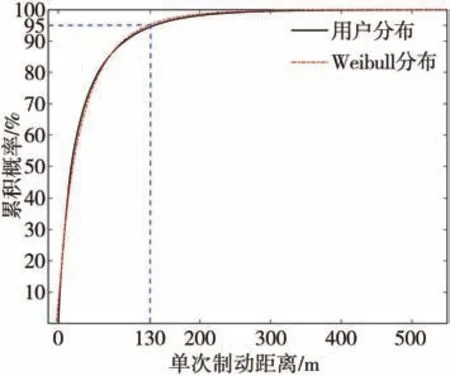
圖7 單次制動距離累積概率分布

從圖6中可得，總體的單次制動距離小于200 m。從圖7中可得，95%單次制動距離小于130 m。

2.4 制動強度分析

由于制動強度的變化會引起工況載荷變化，其大小將直接影響電子助力制動器各部件的性能退化量，所以基于用戶運行數據分析實際制動工況下制動強度的特征尤為重要。根據提取出的制動工況片段計算每個片段的制動強度，得到每個制動片段相對應的制動強度。其中，制動強度計算公式為

式中：vt為制動末速度；v0為制動初速度；Δt為制動持續時間；g為重力加速度，g=9.8 m∕s2。

將得到的所有制動工況片段對應的制動強度進行分布擬合。制動強度服從廣義極值分布［12］，其概率分布和累積概率分布如圖8和圖9所示。

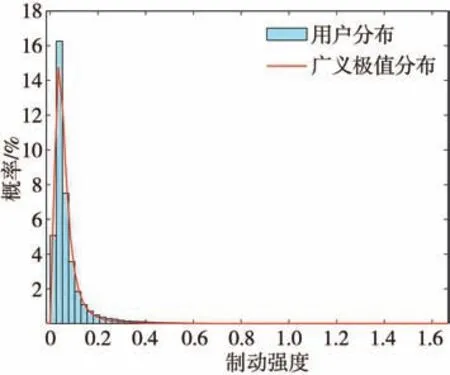
圖8 制動強度概率分布

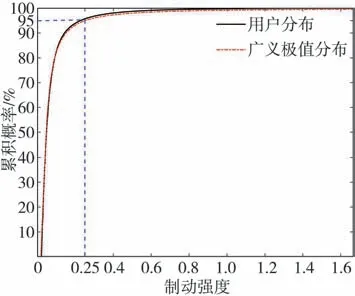
圖9 制動強度累積概率分布

從圖8中可得，總體的制動強度在0.4以下。從圖9中可得，95%制動強度在0.25以下。

2.5 速度變程與制動時間聯合分布

統計每個制動片段的制動速度變程（制動初速與制動末速之差），將速度變程與制動時間聯合分布，如圖10所示。由圖10可知，制動工況主要分布在速度變程小于10 m∕s、制動時間小于10 s的區間。

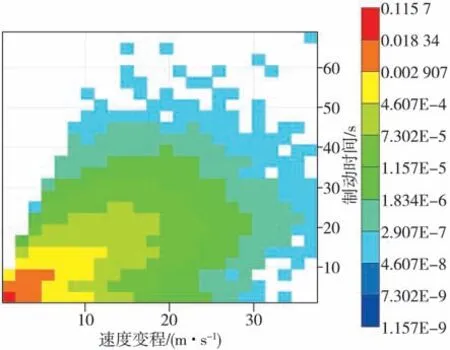
圖10 速度變程和制動時間聯合分布圖

2.6 平均制動強度與最大制動強度聯合分布

統計每個制動工況片段中最大制動強度與平均制動強度，最大制動強度和平均制動強度聯合分布如圖11所示。由圖11可知，制動工況主要分布在平均制動強度小于0.25及最大制動強度小于1.6的區間。

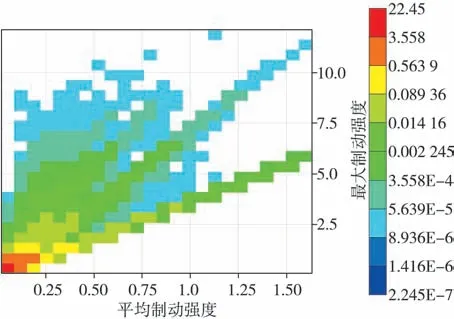
圖11 平均制動強度和最大制動強度聯合分布圖

2.7 總體制動強度頻次分布

以每個用戶為單位，將提取出的制動強度按照區間組頻次統計，先對制動強度進行掃描，找出其最大值與最小值，然后以0.05為一個區間進行區間分組，鑒于制動強度最小值為0，總區間個數為

式中：N為總區間個數；Zmax為制動強度最大值為向上取整運算符。

制動強度各區間組的上限值Ziup和下限值Zidown可以分別按式（4）和式（5）計算。

式中i為區間序號，其最大值為N。

通過每個用戶年運行數據計算年行駛里程，根據年行駛里程將制動強度外推至全壽命周期30萬km，按照區間劃分依據對制動強度在區間組頻次計數，得到各用戶的制動強度區間頻次。從300個用戶中隨機選取30個用戶為例，制動強度累積頻次如圖12所示。

圖12 不同用戶制動強度累積頻次

3 制動工況損傷分析

3.1 制動工況載荷轉換

基于臺架試驗（圖13）標定數據，制動強度與制動壓強之間存在如下關系：

圖13 電子助力制動器臺架試驗

式中：p為制動壓強，MPa；Z為制動強度。

根據式（6），制動壓強與制動強度之間具有較好的線性關系，單位制動強度等效為：10 MPa制動壓強。

電子助力制動器核心部件為大齒輪、小齒輪、反應盤和閥體，服役時處于動態交變載荷下，不同零部件失效主導載荷各不相同。對于齒輪［13］主要是復雜運行工況下交變轉矩引起的疲勞斷裂；對于反應盤和閥體［14］，服役過程中作為動力輸入和傳遞的關鍵性部件，機械應力是導致失效的外因。在不同的制動壓強水平下，作用到各零部件的載荷大小也各不相同，根據臺架試驗不同制動壓強下對各零部件的實測載荷，得到制動壓強與各零部件工況載荷之間關系，如圖14所示。

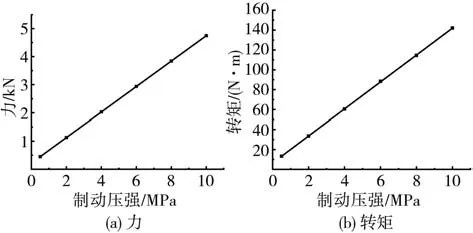
圖14 制動壓強與載荷關系曲線

基于用戶運行數據，通過提取制動工況片段得到每個片段相對應的制動強度，根據臺架試驗數據，得到制動強度與制動壓強之間和制動壓強與載荷之間的關系，實現用戶運行數據向工況載荷的轉換。

3.2 用戶損傷分析

電子助力制動器工作過程中齒輪、反應盤、閥體失效主要表現為往復機械載荷下的疲勞破壞，為評估用戶使用條件下助力器上述部件損傷情況，以疲勞損傷理論為基礎，采用Miner線性損傷累積準則［15］對不同制動強度損傷進行疊加，得到總疲勞損傷。應力幅為S1的載荷引起的損傷為有n1個應力幅為S1的載荷作用時引起的損傷為則總疲勞損傷為

式中：u為級數；Ni為在第i個載荷作用下對應的疲勞壽命；ni為第i個載荷作用的循環次數。

根據疲勞壽命計算方法［16］，有

式中：S為應力幅；N為壽命；m和C為材料常數。

將式（7）和式（8）聯立可得總疲勞損傷：

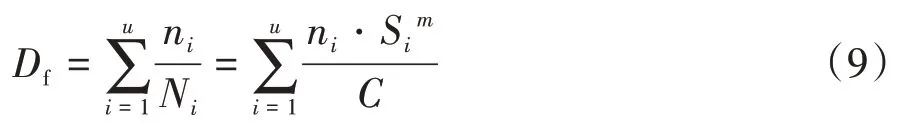
式中Si為第i個應力幅。

用戶最大制動強度為1.6，按照臺架試驗等效轉換取最大制動壓強為16 MPa。采用單獨子模型的方法，以0.5 MPa為一個等級，并將制動壓強轉換為相應的力與轉矩對各部件進行有限元仿真分析，各部件的數值仿真結果如圖15所示。

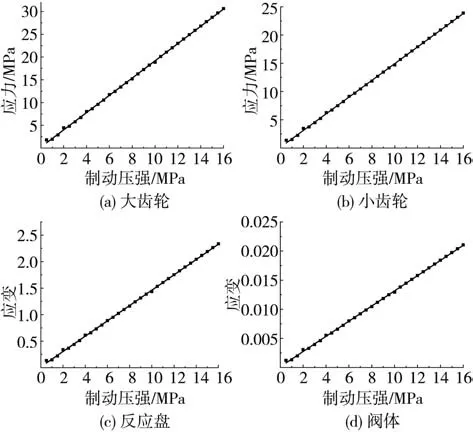
圖15 不同制動壓強各部件應力應變結果

以各部件的數值仿真結果，根據式（9）計算得到不同制動壓強下各部的單次疲勞損傷分布，計算結果如圖16所示。

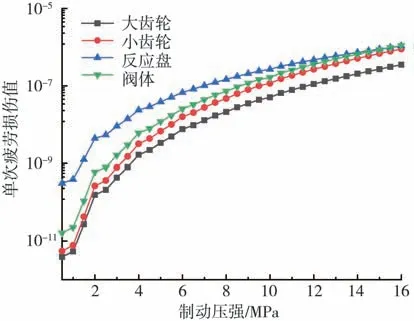
圖16 各部件單次疲勞損傷分布

以隨機選取的30個用戶制動強度頻次，結合各部件的單次疲勞損傷，得到30個用戶對各部件造成的總損傷，由此確定出各部件的用戶損傷累積概率分布模型，如圖17所示。由圖17可知，用戶載荷作用下各部件的損傷服從3參數對數正態分布，大齒輪、小齒輪、反應盤和閥體對應的95百分位損傷值分別為0.017、0.045、0.080和0.055。

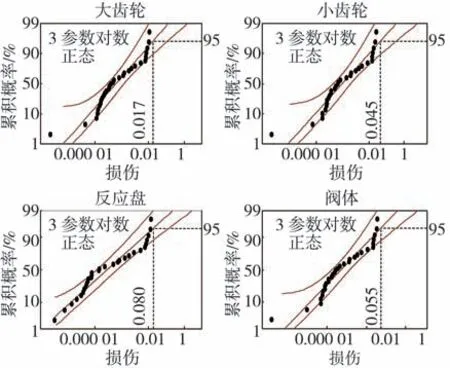
圖17 不同用戶各部件損傷累積概率圖

3.3 典型工況損傷分析

以不同制動壓強下各部件的損傷為基礎，計算各部件在不同制動壓強下的損傷貢獻率，計算結果如圖18所示。由圖18可知，各部件的損傷貢獻率分布趨勢基本一致。0.5～14.5 MPa時，損傷貢獻率基本逐漸增大，制動壓強達到14.5 MPa時損傷貢獻率最大，分析其原因為強制動單次疲勞損傷高，但由于作用次數少而造成的總損傷低，因此對于臺架試驗可選擇最大制動壓強為14.5 MPa；在弱制動時，閥體損傷貢獻率較高；強制動時，反應盤損傷貢獻率較高。針對各部件損傷貢獻的分析，可篩選出高損傷強度的典型工況，為后續總成∕零部件加速試驗工況的選取提供參考。

圖18 不同制動壓強下各部件損傷貢獻

4 標準工況對比

4.1 頻次對比

將隨機選取的30個用戶制動強度頻次分布與現有的AKB-Ⅰ、AKB-Ⅱ、AKB—2016規范標準進行對比，如圖19所示。由圖19可知：AKB-Ⅰ和AKB-Ⅱ的載荷大、工況少、作用頻次少、關聯用戶弱；AKB—2016工況等級多，作用次數也大幅提高，但仍無法滿足95百分位用戶覆蓋度的要求，也無法覆蓋用戶實際使用條件下的極端工況載荷。因此，現有的電子助力制動器可靠性規范難以有效復現用戶實際使用條件下的制動頻次水平。

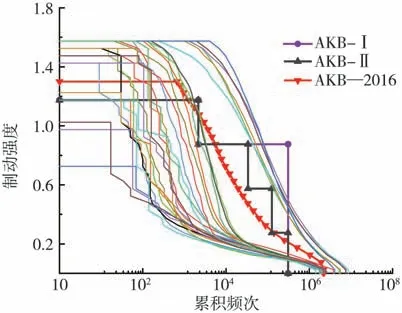
圖19 用戶與標準頻次對比

4.2 損傷對比

將大齒輪、小齒輪、反應盤、閥體損傷分布擬合得到的95百分位損傷與AKB-Ⅰ、AKB-Ⅱ、AKB—2016可靠性規范對各部造成的損傷進行對比，結果如圖20所示。由圖可知：AKB—2016和AKB-Ⅱ對各部件造成的損傷均較低，不符合產品可靠性評價覆蓋高用戶百分位的一般要求；對于AKB-Ⅰ，由于其工況少、載荷大，對各部件的考核難以達到一致水平，齒輪、反應盤過考核，閥體又考核不足，直接影響了可靠性試驗的有效性。因此，現有的電子助力制動器可靠性評價規范難以有效復現用戶實際使用條件下的損傷水平。

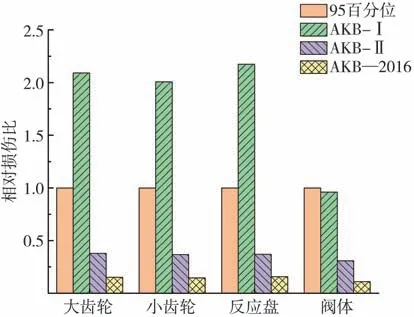
圖20 相對用戶95百分位各部件損傷比

5 結論

本文中以實際用戶運行數據為基礎，通過提取制動工況片段對用戶使用條件下制動工況特征進行分析，包括制動時間、制動距離、制動強度和工況損傷，為電子助力制動器全壽命周期可靠性目標的確定奠定了基礎，主要結論如下。

（1）分析用戶總體制動工況特征，得到用戶總制動時間與里程占比分別為27%和34%。

（2）對制動時間、制動距離、制動強度分布進行分析。其中，制動時間服從對數正態分布，總體上制動時間在20 s以內，95%制動時間在11.56 s以內；制動距離服從Weibull分布，總體上制動距離小于200 m，95%制動距離小于130 m；制動強度服從廣義極值分布，總體上制動強度小于0.4，95%制動強度小于0.25。

（3）用戶實際制動工況下，總體制動特征主要分布在速度變程小于10 m∕s和制動時間小于10 s的區間，平均制動強度小于0.25和最大制動強度小于1.6的區間。

（4）分析不同用戶制動工況載荷下典型部件的損傷分布，得到大齒輪、小齒輪、反應盤和閥體的用戶95百分位疲勞損傷分別為0.017、0.045、0.080和0.055；分析不同制動壓強下損傷貢獻，制動壓強為14.5 MPa時損傷貢獻最大，為臺架試驗最大制動壓強的選取提供參考。

（5）將用戶實際制動工況與標準工況對比，結果表明，現有的可靠性試驗規范不能覆蓋高用戶百分位的一般要求，難以有效地復現用戶實際使用條件下的制動水平。

電子助力制動系統是機-電-液一體化的復雜系統，服役過程中受到力、熱、電等多物理載荷耦合作用，不同部件失效機理各不相同。本文中以電子助力制動系統助力器機械結構為對象，研究其可靠性工況特征，對于電機、控制器、執行器尚未考慮，今后將進一步從力-熱-電多物理載荷損傷耦合效應出發，深入開展電機、控制器、執行器一體化的全壽命周期可靠性目標與工況構成，從而制定更加合理的電子助力制動系統可靠性評價規范。