圖像信息驅動的抑制式粗糙模糊聚類分割算法

趙 鳳 程艷陽 劉漢強 劉 琳

(1. 西安郵電大學通信與信息工程學院 (人工智能學院), 陜西西安 710121; 2. 西安郵電大學電子信息現場勘驗 應用技術公安部重點實驗室, 陜西西安 710121; 3. 陜西師范大學計算機科學學院, 陜西西安 710119)

1 引言

圖像是人類視覺的基礎,是自然景物的客觀反映,是人類認識世界和人類本身的重要源泉,是客觀對象的一種相似性的、生動性的描述或寫真,是人類社會活動中最常用的信息載體。隨著多媒體技術的發展,圖像大數據時代已經來臨。圖像數據在工業生產、醫療健康、遙感識別、軍事競爭以及日常生活中無處不在,對圖像進行智能化處理和分析逐漸成為科學和技術前沿。圖像分割作為圖像處理中的關鍵步驟,是圖像識別和計算機視覺至關重要的預處理,沒有正確的分割就不可能有正確的識別。圖像分割質量對于后續的圖像分析和理解至關重要,對其進行研究仍是一項任重而道遠的工作。從數學角度來看,圖像分割是將數字圖像按照某種規律劃分為多個區域的過程,從而使得被劃分在同一塊區域內的像素可以表現出相似性或者一致性,而那些不在同一塊區域間則會表現出明顯的差異性。圖像的分割方法主要包括以聚類為基礎的分割方法[1-2]、以閾值為基礎的分割方法[3-5]、以區域為基礎的分割方法[6-7]、以邊緣為基礎的分割方法[8-9]和以圖論為基礎的分割方法[10-12]等。基于聚類的圖像分割是將圖像中的像素依據某種聚類準則從而劃分成多個類的過程,盡可能的將相似的樣本點劃分為一類,而具有明顯的差異性的樣本盡可能劃分到不同的類中來實現圖像的分割。眾所周知,圖像是一類典型的含有不確定性的數據。為了有效處理圖像中的模糊性和不確定性,許多學者研究基于模糊聚類的圖像分割方法。CaiOck-Kyung Yoon[13]提出了一種基于模糊聚類的腦磁共振圖像分割方法,實現對白質、灰質和腦脊髓液的自動分割。Zhao[14]等人提出了一種提升的空間模糊C-均值聚類算法,通過引入空間約束項提升方法的抗噪能力。Zhao[15]等人利用像素的鄰域統計信息和競爭性學習思想構建圖像的直覺模糊集,從多目標優化的角度,提出了一種新穎的噪聲魯棒的多目標進化直覺模糊聚類算法。

粗糙集理論是繼概率論、模糊集、證據理論之后的又一個處理不確定性問題的數學工具。1982年,波蘭數學家Z.Pawlak提出了粗糙集理論[16],用來研究不完整數據,不精確知識表達、學習、歸納等的一套理論。2002年,Lingras等人[17]把粗糙集理論中的上、下近似引進到C-均值算法中,提出了粗糙C-均值算法。Seiki Ubukata[18]等人將粗糙集理論引入到硬C-medoids聚類中并參考廣義粗糙C-均值提出了粗糙C-medoids聚類,處理樣本歸屬的確定性、可能性和不確定性。由于圖像數據的不確定性,粗糙聚類應用于實際的圖像分割時,容易出現類間像素重疊的問題。為此,將模糊聚類與粗糙聚類相結合的方法被更多地應用于圖像分割問題,試圖從多種信息處理角度挖掘圖像數據的模糊性和不確定性。粗糙模糊聚類[19]整合了模糊集和粗糙集理論[20]的優點,已經顯示出它們在圖像分割中的有效性[21],有效處理了圖像中的各種不確定性。例如,Shaswati Roy等人[22]提出了一種基于模糊粗糙聚類和空間約束的算法,避免了圖像偽影造成的敏感性問題,使用粗糙集的核心區域和邊界區域的概念處理了簇定義中的不完整性,可以有效地處理重疊分區,在醫學圖像分割上獲得了良好的性能。

傳統的粗糙模糊聚類方法應用于圖像分割時,需要手動設置合適的閾值確定粗糙聚類的上、下近似,閾值的選取不同會對實驗結果造成一定的影響。此外,該算法對于圖像中的噪聲較為敏感。為了克服這些問題,本文提出一種圖像信息驅動的抑制式粗糙模糊聚類分割算法,實現粗糙模糊聚類在圖像分割中的深度應用。該算法設計了基于超像素區域信息的自適應閾值確定策略,用于判定聚類的上、下近似。該策略首先對輸入圖像進行超像素區域劃分,并對超像素區域的代表特征進行初步聚類獲取超像素區域對初步聚類中心的模糊隸屬度,進而獲取判定粗糙聚類的上、下近似的閾值。將自適應閾值策略應用到粗糙模糊聚類中,極大的降低了由于人為選取閾值不當造成的誤差。為了克服方法對于圖像噪聲的敏感性,將圖像空間信息引入到粗糙模糊聚類,構造了融合空間信息的粗糙模糊聚類目標函數。此外,在聚類迭代過程中將模糊聚類中的抑制式學習思想引入到粗糙下近似集中像素的模糊隸屬度的修正中,進一步提升聚類性能,使得粗糙聚類與模糊聚類深度融合,可以從多個不同角度更加精細處理圖像數據的模糊性和不確定性。綜上,本文算法是更具混合智能機理的粗糙模糊聚類圖像分割算法,自適應閾值有效性驗證實驗以及Berkeley[23]圖像對比實驗證明了本文算法的有效性。

2 圖像信息驅動的抑制式粗糙模糊聚類分割算法

2.1 基于超像素的自適應閾值確定

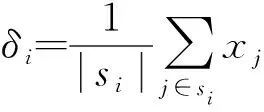
(1)

假設μip和μiq分別為代表點i對應的最大隸屬度和次大隸屬度,利用下式構造上下近似判斷的自適應閾值T,

(2)

2.2 融合圖像空間信息的粗糙模糊聚類目標函數

傳統的粗糙模糊聚類算法在應用于圖像分割時,沒有考慮圖像中的任何空間信息,這樣使得算法對于圖像中的噪聲敏感,無法在含噪圖像分割中獲得滿意的分割效果,為了解決這個問題,本文構造了融合圖像空間信息的粗糙模糊聚類目標函數,具體如下:

(3)

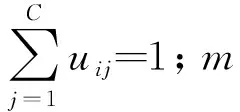
(4)

其中p表示像素i的ω×ω鄰域內像素的集合。為了最小化目標函數,采用Lagrange乘子法,獲得中心和隸屬度的更新公式:

(5)

(6)

2.3 基于自適應閾值的粗糙上下近似的確定

依據公式(6)獲得的像素點與聚類中心之間的模糊隸屬度,計算像素i對應的最大隸屬度uip和次大隸屬度uiq,基于2.1部分獲得的自適應閾值,按照下式確定融合空間信息的粗糙下近似和邊界,

(7)

即當某個像素點最大隸屬度和次大隸屬度的差值大于自適應閾值時,這個像素點會被劃分到下近似中;否則,該像素點被劃分到邊界中。

2.4 抑制式粗糙下近似策略

為了加速算法收斂并提升算法性能,將模糊聚類中的抑制式學習思想引入到粗糙下近似集中像素的模糊隸屬度的修正中,通過借助競爭學習的思想,在每一次的迭代過程中,對下近似集中像素的最大隸屬度uip進行適當的放大,其他隸屬度給以適當的抑制達到加速粗糙模糊聚類收斂的效果。下式為隸屬度修正計算公式:

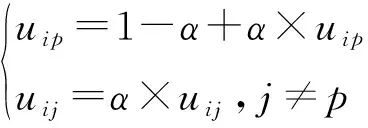
(8)

其中α指的是抑制參數。所以在每一次的聚類迭代更新過程中,需要將修正后的隸屬度代入中心更新公式中。

2.5 算法流程

本文提出的圖像信息驅動的抑制式粗糙模糊聚類分割算法的主要步驟介紹如下:

算法1 圖像信息驅動的抑制式粗糙模糊聚類分割算法輸入:圖像數據X,模糊指數m,聚類數目K,下近似權重系數Wl,邊界權重系數Wb,迭代停止閾值ε,空間限制參數β,抑制參數α,最大迭代次數Iter。步驟1 采用基于超像素區域信息的自適應閾值確定策略獲得圖像X的自適應閾值T;步驟2 隨機初始化聚類中心vj;步驟3 設置初始迭代次數t=0;步驟4 按照公式(5)計算融合空間信息的模糊隸屬度;步驟5 按照公式(8)對隸屬度進行抑制式變換;步驟6 按照公式(7)將修正后的最大隸屬度與次大隸屬度的差與自適應閾值進行比較,從而進行粗糙模糊聚類的上下近似劃分;步驟7 按照公式(6)更新聚類中心;步驟8 如果vt+1-vt2≤ε,迭代終止;否則令t=t+1,返回步驟4;輸出:圖像分割結果。

3 實驗結果與分析

3.1 實驗設置

為了驗證本文所提出的算法的有效性,本文選取了Berkeley圖庫中的圖像進行分割實驗并采用粗糙聚類、粗糙模糊聚類、基于空間信息的模糊聚類(Fuzzy C-Means with neighborhood-based spatial constraints, FCM-S)以及抑制式模糊聚類(Suppressed Fuzzy C-Means, SFCM)算法作為本文實驗的對比算法。實驗中,采用分割準確率指標[25](Segmentation Accuracy, SA)、標準化互信息指數[26](Normalized Mutual Information, NMI)以及蘭德指數[26](Rand Index, RI)來驗證所有算法的有效性。SA指標越高表明圖像的分割效果越好。NMI和RI兩個指標則進一步驗證了聚類的效果好壞,當數值越大,代表聚類效果越好。

在本文算法中,空間限制參數β可以控制空間信息在算法中重要性,對圖像分割性能有一定的影響,我們通過對比在不同大小的β下分割圖像的準確率,將分割準確率隨參數的變化曲線展示在圖1中,從結果中可以看出,當沒有空間限制參數時(β=0),提出的方法在含噪圖像上沒有獲得理想的分割性能,由此驗證了空間信息的有效性。在給定均值為0、標準方差為0.01的高斯噪聲時,綜合評價三幅圖像的性能曲線,β取10是最合適的。

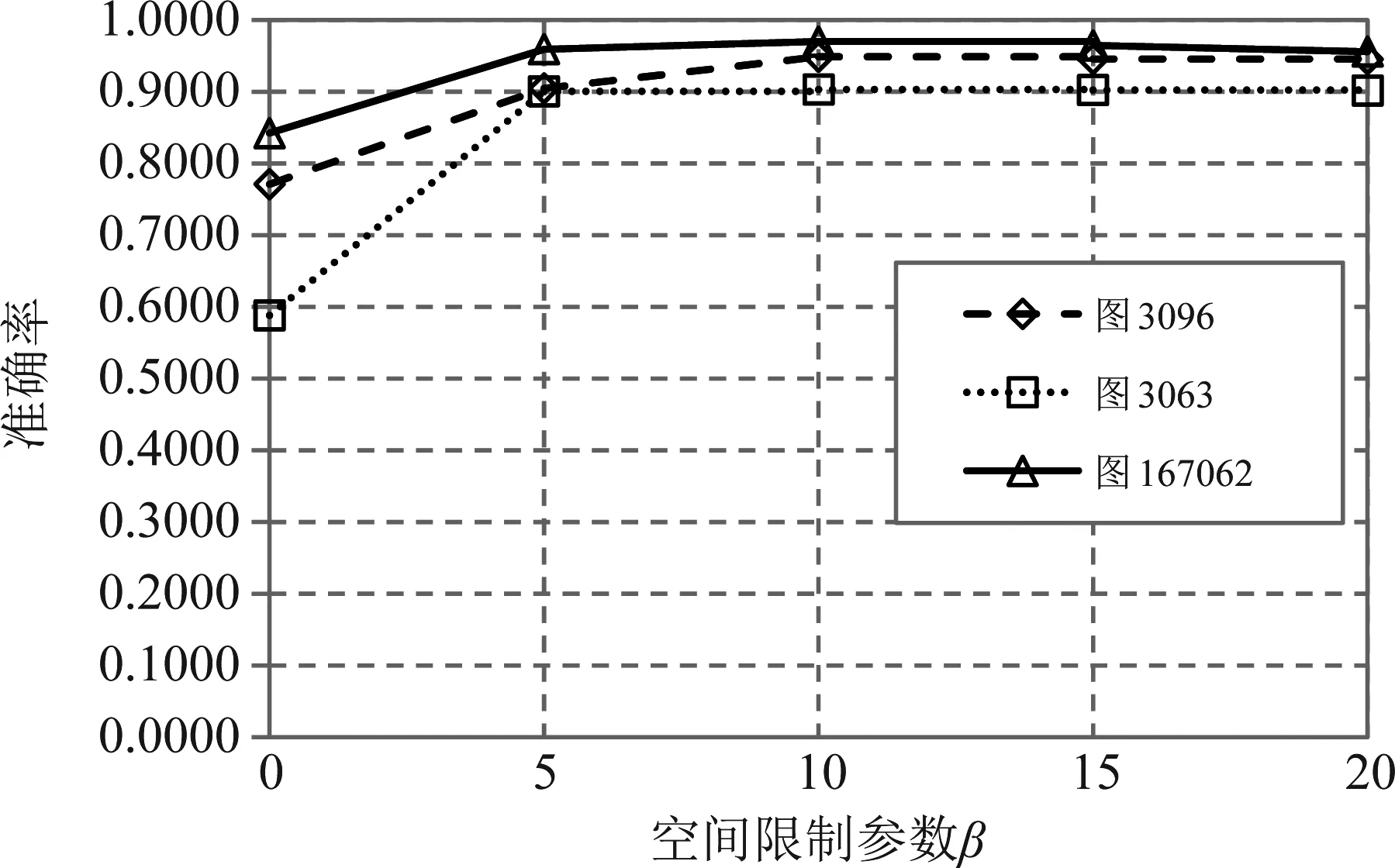
圖1 不同分割圖像在不同空間項系數下的準確率Fig.1 Accuracy of different segmented images under different spatial coefficients

由文獻[27]可知,模糊指數m一般取2是合適的,并且依據大量實驗經驗,權重系數Wl和Wb在粗糙聚類、粗糙模糊聚類和本文算法中均分別設置為0.7和0.3。所有比較算法的部分參數設置如表1所示。

表1 三種算法的參數設置

3.2 自適應閾值策略有效性驗證實驗

為了驗證本文算法所提出的自適應閾值策略的有效性,將自適應閾值策略應用于粗糙模糊聚類算法,并與該算法分別在0.1、0.3、0.5、0.7、0.9等不同閾值下得到的分割結果圖像進行了對比。實驗結果如圖2～圖6所示。

從圖2～圖6中可以看出,本文所提出的自適應閾值策略可以得到較為理想的分割效果,減少了人為干預,降低了手動設置閾值所造成的誤差。

圖2 不同閾值下的圖像3096分割結果Fig.2 Image 3096 segmentation results under different thresholds

圖3 不同閾值下的圖像3063分割結果Fig.3 Image 3063 segmentation results under different thresholds

圖4 不同閾值下的圖像238011分割結果Fig.4 Image 238011 segmentation results under different thresholds

圖5 不同閾值下的圖像101027分割結果Fig.5 Image 101027 segmentation results under different thresholds

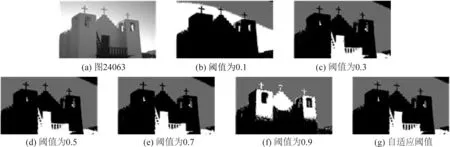
圖6 不同閾值下的圖像24063分割結果Fig.6 Image 24063 segmentation results under different thresholds

3.3 Berkeley圖像對比實驗

為了驗證所提出的算法在含噪圖像上的分割效果,在八幅Berkeley圖像上人為添加了均值為0、標準方差分別為0.005和0.01的高斯噪聲,并在表2和表3中展示了不同噪聲下所有比較方法的分割準確率,在表4和表5中展示了不同噪聲下所有比較方法的標準化互信息指數,在表6和表7中展示了不同噪聲下所有比較方法的蘭德指數。需要指出,粗糙聚類算法和粗糙模糊聚類算法需要給定合適的閾值來粗糙聚類的劃分上、下近似。根據不同閾值下的實驗數據表明,粗糙聚類算法對于圖3096、圖3063、圖167062,閾值選取為6.4是比較合適的;對于圖238011、圖15088、圖101027,閾值選取為8.1是比較合適的,對于24063、圖86016,閾值選取為10.4是比較合適的。在粗糙模糊聚類算法中,對于圖3096、圖86016、圖15088,閾值選取為0.3是比較合適的;對于圖238011、圖3063、圖167062,閾值選取為0.1是比較合適的;對于圖101027、圖24063,閾值選取為0.5是比較合適的。從表2～表7中可以看出,本文提出的方法在大多數被噪聲污染的圖像上都獲得了理想的分割性能。

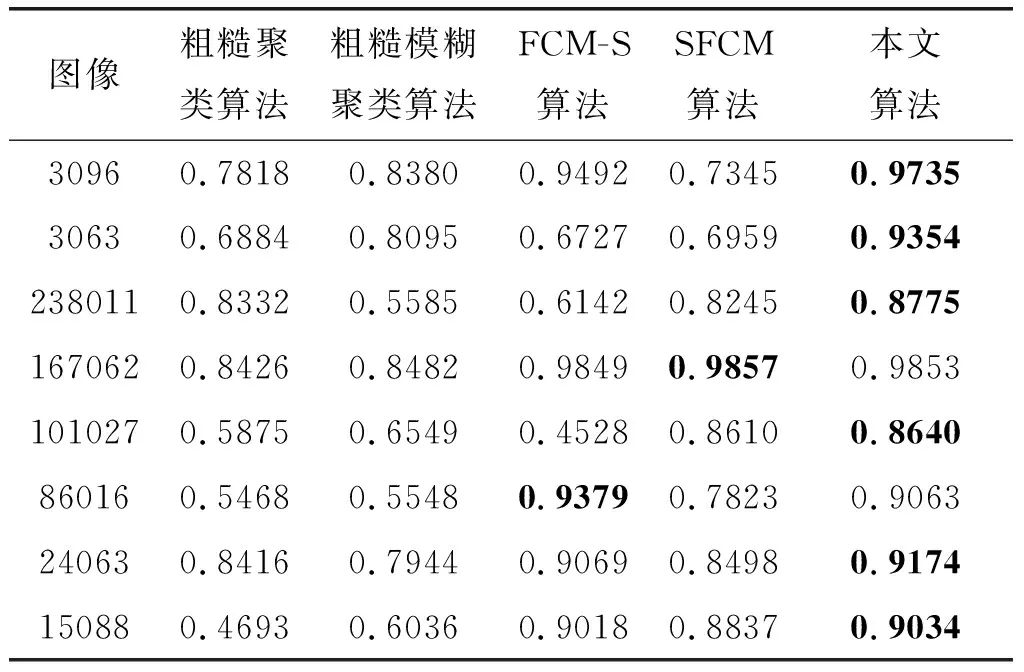
表2 均值為0、標準方差為0.005高斯噪聲 污染下的圖像分割準確率

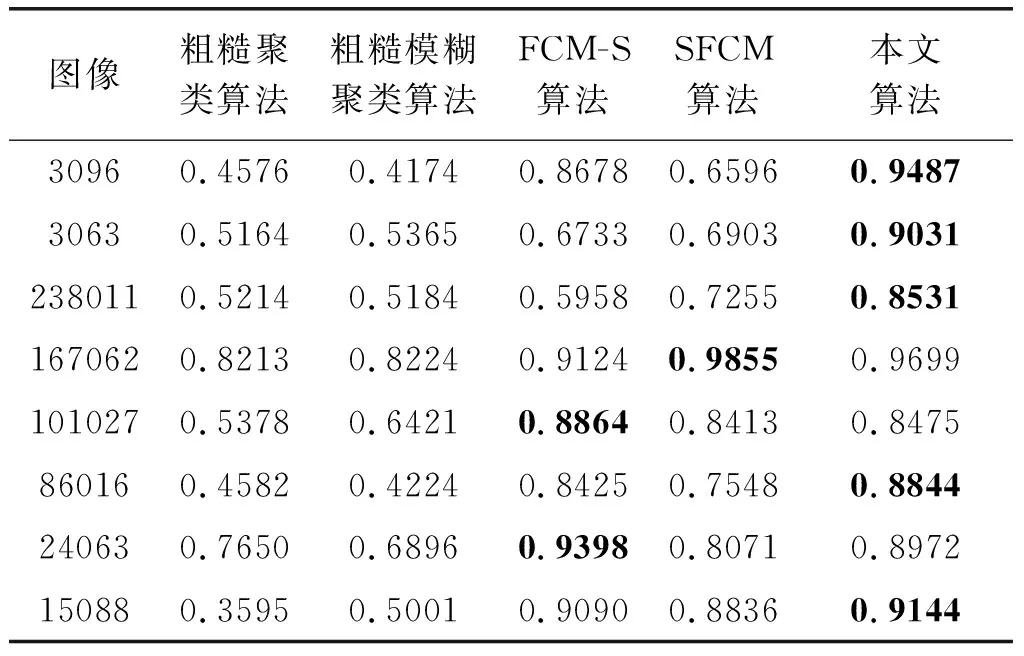
表3 均值為0、標準方差為0.01高斯噪聲 污染下的圖像分割準確率

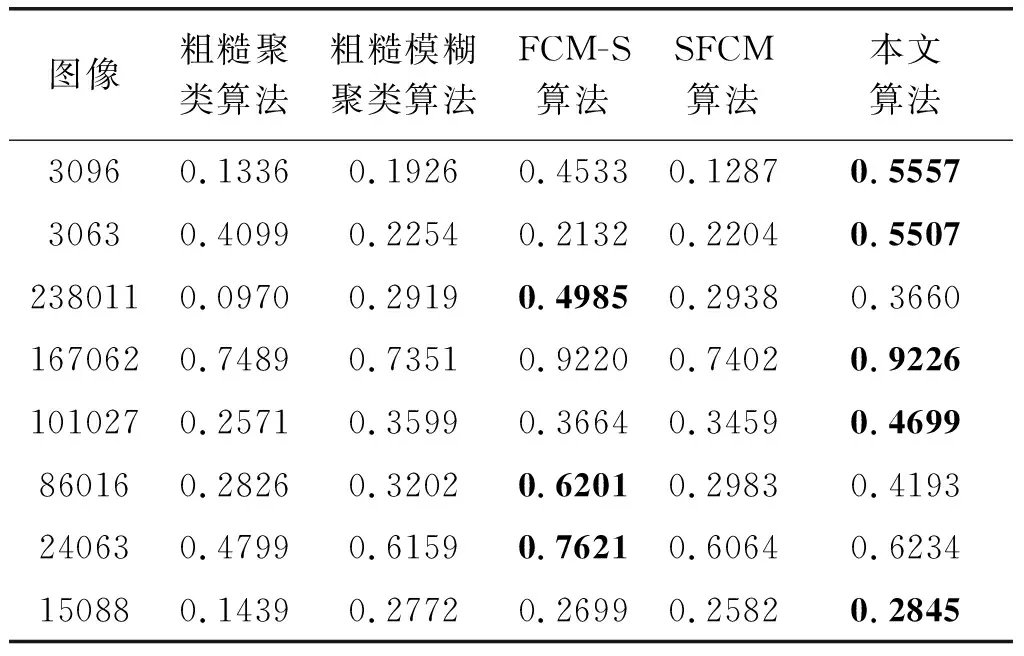
表4 均值為0、標準方差為0.005高斯噪聲 污染下的圖像標準化互信息指數

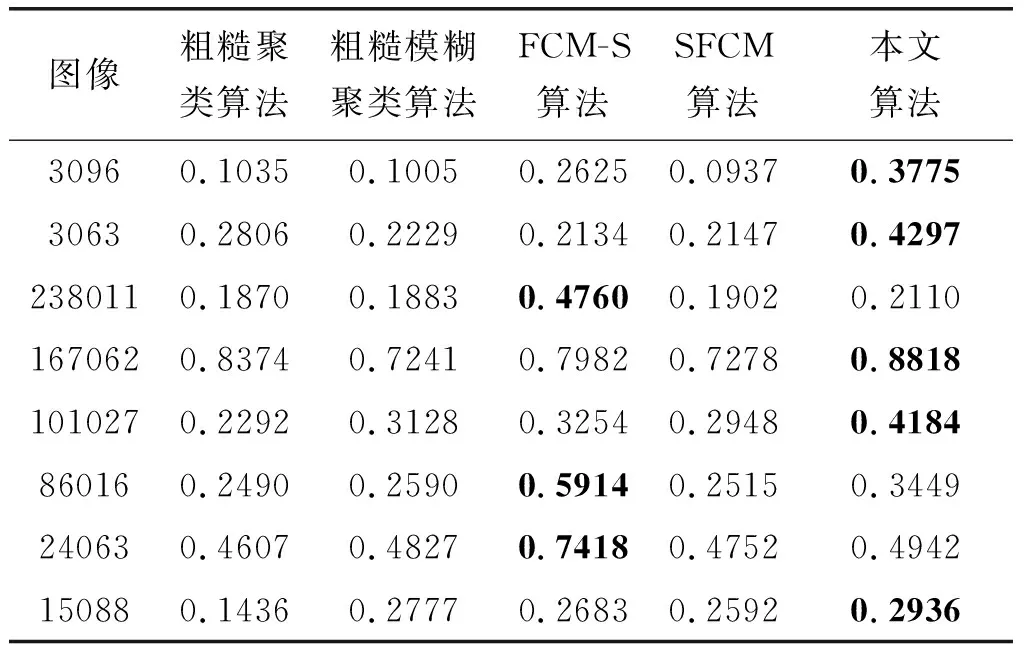
表5 均值為0、標準方差為0.01高斯噪聲 污染下的標準化互信息指數

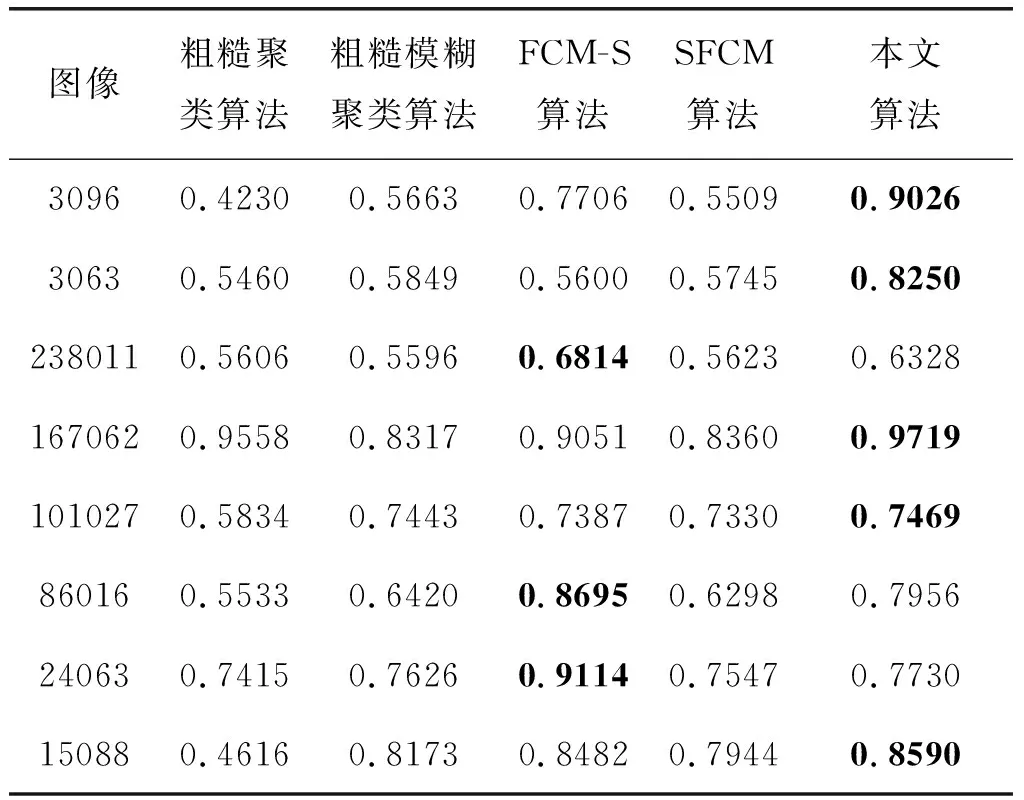
表7 均值為0、標準方差為0.01高斯噪聲 污染下的蘭德指數

為了更直觀的展示含噪圖像的視覺分割結果,在圖7～圖22中,展示了被不同噪聲污染的八幅圖像的分割結果。結合空間信息的FCM-S算法和本文提出的算法獲得視覺分割結果明顯優于其他分割方法,由于采用了粗糙和模糊理論相結合的思想,分割結果中的目標更加準確,且背景噪聲更少且錯分更少,因此本文提出的方法獲得了更加理想的分割結果。

圖7 均值為0、標準方差為0.005高斯噪聲污染下的圖像3096分割結果Fig.7 Segmentation results of 3096 image corrupted by Gaussian noise with zero mean and standard variance 0.005

圖8 均值為0、標準方差為0.005高斯噪聲污染下的圖像3063分割結果Fig.8 Segmentation results of 3063 image corrupted by Gaussian noise with zero mean and standard variance 0.005

圖9 均值為0、標準方差為0.005高斯噪聲污染下的圖像238011分割結果Fig.9 Segmentation results of 238011 image corrupted by Gaussian noise with zero mean and standard variance 0.005

圖10 均值為0、標準方差為0.005高斯噪聲污染下的圖像167062分割結果Fig.10 Segmentation results of 167062 image corrupted by Gaussian noise with zero mean and standard variance 0.005

圖12 均值為0、標準方差為0.005高斯噪聲污染下的圖像86016分割結果Fig.12 Segmentation results of 86016 image corrupted by Gaussian noise with zero mean and standard variance 0.005

圖13 均值為0、標準方差為0.005高斯噪聲污染下的圖像24063分割結果Fig.13 Segmentation results of 24063 image corrupted by Gaussian noise with zero mean and standard variance 0.005

圖14 均值為0、標準方差為0.005高斯噪聲污染下的圖像15088分割結果Fig.14 Segmentation results of 15088 image corrupted by Gaussian noise with zero mean and standard variance 0.005

圖15 均值為0、標準方差為0.01高斯噪聲污染下的圖像3096分割結果Fig.15 Segmentation results of 3096 image corrupted by Gaussian noise with zero mean and standard variance 0.01

圖16 均值為0、標準方差為0.01高斯噪聲污染下的圖像3063分割結果Fig.16 Segmentation results of 3063 image corrupted by Gaussian noise with zero mean and standard variance 0.01

圖17 均值為0、標準方差為0.01高斯噪聲污染下的圖像238011分割結果Fig.17 Segmentation results of 238011 image corrupted by Gaussian noise with zero mean and standard variance 0.01

圖18 均值為0、標準方差為0.01高斯噪聲污染下的圖像167062分割結果Fig.18 Segmentation results of 167062 image corrupted by Gaussian noise with zero mean and standard variance 0.01

圖19 均值為0、標準方差為0.01高斯噪聲污染下的圖像101027分割結果Fig.19 Segmentation results of 101027 image corrupted by Gaussian noise with zero mean and standard variance 0.01

圖20 均值為0、標準方差為0.01高斯噪聲污染下的圖像86016分割結果Fig.20 Segmentation results of 86016 image corrupted by Gaussian noise with zero mean and standard variance 0.01

圖21 均值為0、標準方差為0.01高斯噪聲污染下的圖像24063分割結果Fig.21 Segmentation results of 24063 image corrupted by Gaussian noise with zero mean and standard variance 0.01

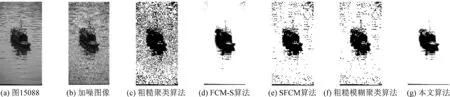
圖22 均值為0、標準方差為0.01高斯噪聲污染下的圖像15088分割結果Fig.22 Segmentation results of 15088 image corrupted by Gaussian noise with zero mean and standard variance 0.01

4 結論

為了從多個不同角度更加精細處理圖像數據的模糊性和不確定性,實現粗糙模糊聚類在圖像分割中的深度應用,并減少人為干預和對圖像中噪聲的敏感性,本文提出一種圖像信息驅動的抑制式粗糙模糊聚類分割算法。算法設計的基于超像素的自適應閾值策略大大降低了手動設置閾值對分割效果造成的影響,空間信息的引入成功抑制了圖像中的噪聲,抑制式學習思想的引入實現了粗糙和模糊思想的深度融合,進一步提升了聚類性能。實驗證明本文所提出的算法在對含噪圖像進行圖像分割時,分割效果明顯優于其他算法。在接下來的研究工作中,如何將粗糙聚類算法與更多現代智能優化算法相互結合從而構造具有混合智能機理的粗糙聚類算法是一個值得繼續探究的問題。