基于SVM-RFE特征選擇的規則提取方法

吳 璐

(上海市規劃和自然資源局 信息中心， 上海 200003)

0 引言

由于支持向量機(Support Vector Machine, SVM)具有堅實的統計學習理論基礎和良好的泛化性能，已經被應用到客戶分類和管理、銀行信用風險評估、故障檢測、地理遙感信息等[1-4]眾多領域中，并取得了較好的成果。然而SVM和人工神經網絡一樣也存在著固有的缺陷，即其“黑箱模型”。人們很難理解其模型代表的意義，也無法對模型的預測結果做出一個合理的解釋。SVM 學習到的知識蘊藏在由占樣本總數很少的支持向量及其權重系數(Lagrange系數)所得到的決策函數中，用戶無法了解SVM 到底學到了什么、能處理什么樣的任務，也無從知道SVM 如何進行分類和預測、為什么得出這樣或那樣的推理結論。由于缺乏透明性，在數據挖掘和決策支持領域、以及在安全性要求很高如醫療診斷方面等關鍵應用方面，支持向量機和神經網絡一樣往往被認為是不可靠的和難以理解的，使其應用受到一定限制。

將支持向量機訓練后生成的決策模型轉變成更加直觀、更易理解的知識的過程被稱為支持向量機規則提取方法。它主要分為基于學習的方法和基于結構分析的方法兩大類[5]。前者比較典型的算法如TREPAN、GEX、BUR等[6]，后者如SVM + prototypes、RulExSVM算法等[7-9]。雖然這些方法在實際應用中取得了一些成果，但從總體上看，這些規則提取方法產生的規則大都數量比較多、精度不高、規則的前提條件項數太多、結構較為復雜，不便于人們的理解和解釋。此外，這些方法對于研究領域的數據維度較高也不能很好地適應。

造成上述問題的主要原因主要在于過于強調準確率和忠實度指標，對可理解性重視不夠以及沒有對樣本屬性進行降維處理提高可理解性。對此本文提出了一種基于SVM-RFE特征選擇(SVM-BASED Recursive Feature Elimination，SVM-RFE)的序列覆蓋規則提取方法，將特征選擇作為整個規則提取的一部分來進行綜合考慮，并在規則生成和裁剪上通過采取包括生成的規則必須滿足最低的精度要求、覆蓋率大的規則優先選取、限制搜索深度和采用FOIL增益對條件項的增加進行評估對可理解性與準確率和忠實度指標之間進行平衡。

1 SVM-RFE特征選擇算法簡介

SVM-RFE特征選擇算法是一種以支持向量機的分類性能作為特征選擇評價標準的后向遞歸消除特征選擇算法，具有較高的識別性能。它最早是由Guyon等[10]在基因選擇中首先提出來的，并將其應用于癌癥分類問題中進行基因選擇，取得了非常好的效果。在這之后許多人又對 SVM-RFE方法進行了進一步的改進以提高它的性能和效率[11-12]，目前已經被廣泛應用于基因表達數據分析、蛋白質功能預測、圖像檢測、文本挖掘等多個領域。

SVM-RFE起始于全部特征，然后每次移去一個特征直到特征集合為空，移去的特征是所有特征中‖w‖2最小的一個。這樣對某一變量i，排序評價準則如式(1)。

(1)

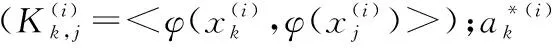
SVM-RFE方法通過不斷迭代方式將具有最小排序系數的特征移除，然后利用SVM對剩余的特征重新訓練以獲取新的特征排序，最后得到一個特征的排序列表。利用該排序列表，定義若干個嵌套的特征子集F1?F2?…?F來訓練SVM，并以SVM的預測正確率評估這些子集的優劣，從而獲得最優的特征子集。

2 基于SVM-RFE特征選擇的規則提取方法的實現

2.1 算法總體框架

基于SVM-RFE特征選擇的規則提取方法的總體架構，如圖1所示。

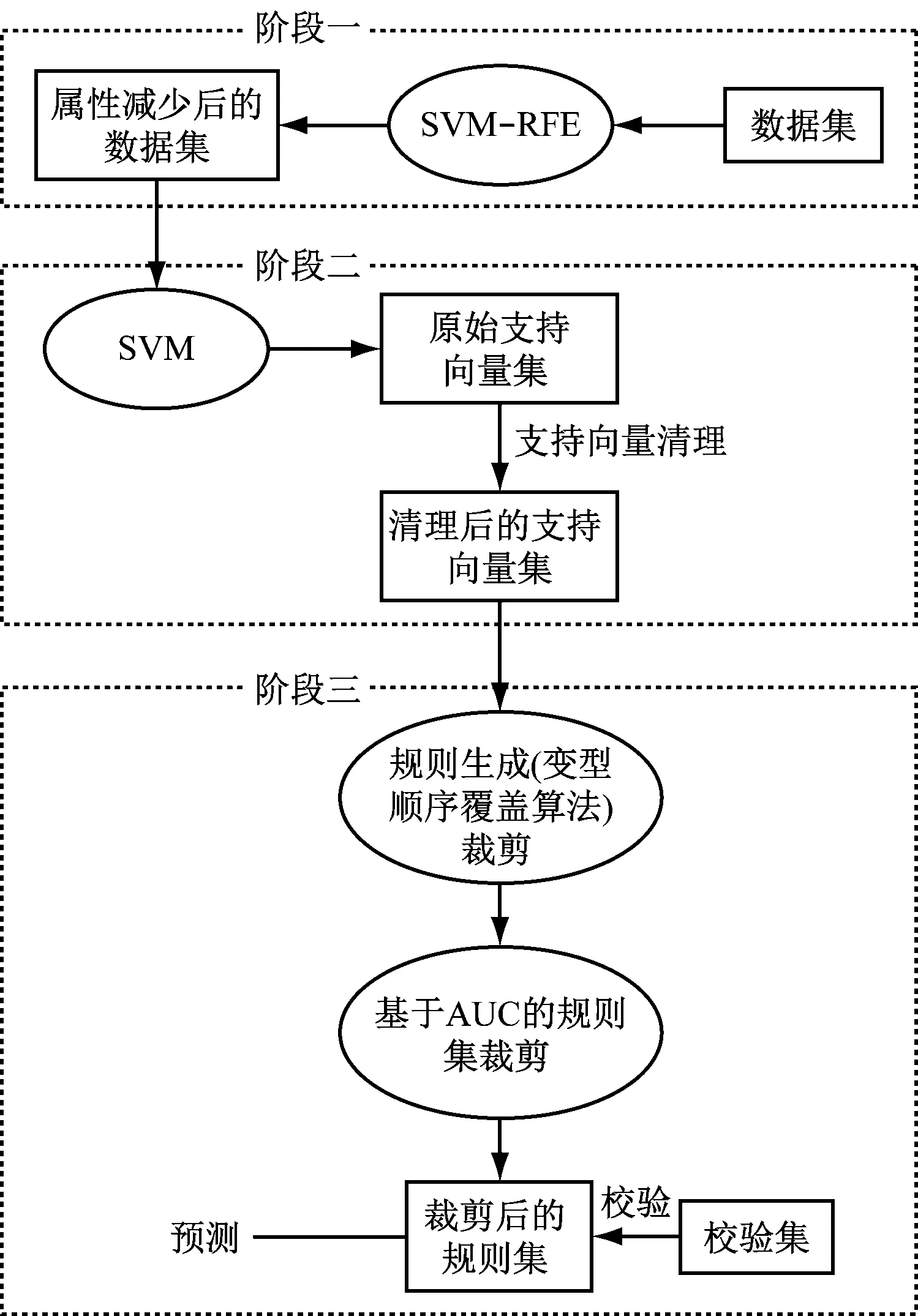
圖1 基于SVM-RFE特征選擇的規則提取知識表示方法的總體框架

主要包括基于SVM-RFE特征選擇、支持向量機學習、規則生成和規則集裁剪等3個階段。

首先，對初始數據集基于SVM-RFE特征選擇算法進行屬性約簡。根據它們在SVM分類器的權值進行重要性排序，得到最優特征子集并去除原屬性集中不相關和弱相關的屬性。在使用SVM-RFE算法進行特征選擇時，為了減少SVM-RFE算法對訓練集的選取較為敏感、特征排序不太穩定的問題，我們通過在樣本集隨機生成多個訓練集并綜合排名的方式進行了優化和改進。

其次，用得到屬性減少的樣本集對支持向量機進行訓練和學習，得到全部支持向量集。去除其中預測分類與樣本原有的類標簽兩者不一致的支持向量，從而生成清理后的支持向量集。

最后，通過一種變型的順序覆蓋規則學習算法對這些清理后的支持向量集進行歸納學習生成規則集，然后通過AUCs的差異顯著性對規則集進行裁剪，得到裁剪后的規則集。用驗證集來對其進行驗證，以確保其準確率(accuracy)滿足規定的要求，通過上述驗證后我們就可以使用得到的規則集來進行預測。本節后面重點對上述提到的這兩部分進行說明。

2.2 基于優化的SVM-RFE算法特征選擇

通過特征選擇可以使提取規則的可理解性得到很大的改善，還能夠提高分類器的識別率。這里采用基于支持向量機的特征選取方法，主要是由于它和支持向量機算法本身結合得更好，能夠保證甚至提高支持向量機的識別精度。

基于支持向量特征選擇選取方法主要分為Wrapper 、Filter和Embedded等[13]3種方法。考慮到Wrapper方法與學習分類器密切相關，構造的特征子集能夠帶來較高的學習能力，因此我們選擇SVM-RFE這種方法，它在處理高維方面能力更強。當然SVM-RFE這種方法也有不足之處，處理速度相對比較慢。但是考慮到對于規則提取來說，特征選擇的好壞更加重要，因此選擇SVM-RFE這種方法還是比較值得的。

在使用SVM-RFE算法進行特征選擇時，針對 SVM-RFE算法對訓練集的選取較為敏感、特征重要性排序不太穩定的問題，我們通過在訓練樣本集隨機生成多個訓練子集并采用綜合排名的方式進行了優化和改進。具體說明如下。

(1) 對于樣本集{(x1,y1),(x2,y2),…,(xl，yl)}，其中xi∈Rd，yi=±1，隨機生成m個訓練子集和測試子集對，其中m的取值根據樣本的數量，屬性維度和特征選擇的精度要求等確定。

(2) 對每一個訓練子集分別用SVM分類器進行訓練，并用徑向基函數作為支持向量機的核函數，這是由于在很多實際應用中發現它們具有較好的效果。懲罰參數和高斯核函數中的參數σ的值通過Grid search和10-fold交叉驗證來確定。

(4) 對于每個特征根據其在最優特征子集出現的頻度和位置，生成一個新的特征排序表。對每一個特征，按照式(2)進行加權求和并按照權值大小降序排序，得到一個新的特征排序表。

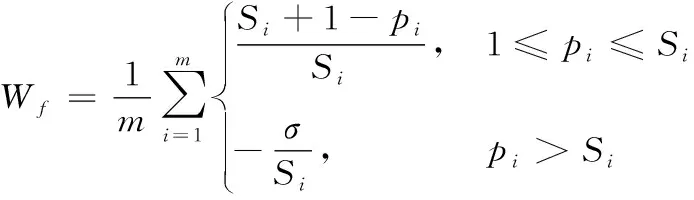
(2)

其中，Si為第i個隨機訓練子集上最優特征子集中特征的數量；pi為特征f在第i個隨機訓練集中最有特征子集中的位置；σ為懲罰系數(σ≥0)，當其值越大特征出現的次數對權值的影響更大。

(5) 根據新的特征排序列表生成d個嵌套子集，在所有的隨機訓練子集上用這些嵌套子集重新訓練SVM分類器，并將這些嵌套子集所訓練的SVM在測試子集上的分類精度進行算術平均，算術平均值最高的所對應的嵌套子集作為最終的最優特征子集。

2.3 基于變型順序覆蓋算法的規則生成

在規則生成和裁剪階段，從基于特征選擇的規則提取的架構上來看，原則上基于學習的規則提取方法如TREPAN、C4.5、BUR、CART等和基于結構分析的提取方法如SVM+ prototypes、RulExSVM都可以直接用來進行規則的提取。 基于在規則提取算法設計和實現上把提高可理解性作為一個重要目標，兼顧可理解性與準確率和忠實度之間的平衡原則，我們還提出了一種變型的順序覆蓋算法(Sequentail Covering Algorithm)將前面所述的一些提高可理解性的策略應用到該算法的實現中以提高生成規則的可理解性。該算法通過對清理后的支持向量集進行歸納學習來生成規則集。

該算法采用從一般到特殊的柱狀搜索方式，它在搜索過程中保留前面k個性能度量較高的選擇以降低只保留最高性能選擇容易造成的局部最優問題。另外它只產生覆蓋正例支持向量的規則，即對于規則沒有覆蓋的實例默認為負例。為了提高規則的可理解性，該算法在學習單個規則的核心子程序Learn-One-Rule的中主要特點說明如下。

(1) 迭代過程中對屬性值的劃分采用動態方式，隨著約束條件的增加不斷調整，并且屬性劃分采用信息增益即式(3)進行性能評估選取最佳分割點；另外在同樣性能條件下，離散屬性優先，如式(3)。

(3)

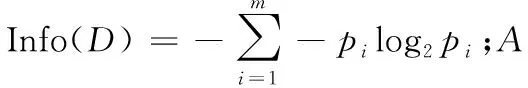
(2) 在搜索過程中為了保證生成的規則有較好的可理解性，強制其最大搜索深度為5，即條件前提項的項數不能超過5，這是因為當前提條件項數超過5個以后一般情況下人們已經不能很好理解。

(3) 在規則性能的度量上，采用FOIL增益即式(4)評估約束條件項增加前后的增益，當該值大于0時增加約束項才是有價值的。在此我們選取該方法的主要原因是與其他性能度量方法相比，FOIL增益更傾向具有高準確率并且覆蓋許多正例的規則，這樣有利于提高規則的可理解性。

(4)

其中,pos(neg)、pos′(neg′) 分別為條件項增加前后規則覆蓋的正(負)例的數目。

(4) 生成的每一條規則都必須滿足一定的精度要求，即其TPR/FPR>(TPR/FPR)min不小于(TPR/FPR)min,從而確保生成的規則有較高的精度。

Learn-One-Rule整個規則生成和裁剪的算法如下。

輸入：

SVs(來自SVM學習階段的結果——調整后的支持向量集)。

特征排序列表F(按照屬性重要性降序排列，來自SVM-RFE的特征選擇)。

(TPR/FPR)min(最小可接受的正例覆蓋率/負例覆蓋率比值)。

輸出：

命題規則集R。

處理：

① 初始化S=SVs。

② 初始化Best_hypothesis=φ，Candidate_hypotheses={Best_hypothesis}。

③ 對于F中的每一個屬性fi， 根據其屬性值在S中的取值范圍，尋找其最佳的閾值aib，它能在所有的樣例S中根據式(3)得到最大的信息增益。

④ 按照上述排序順序，對于F中的每一個屬性fi分別用與其相應的在③中得到的閾值aib生成一個約束ci，生成約束集C。

⑤ 對Candidate_hypotheses中的每個假設h，按照特征排序列表F的順序添加約束集C中沒有添加過的約束，如已無法添加則直接刪除。對于添加后的規則用式(4)評估其添加約束前后的FOIL增益，當其小于0時，將該條規則予以刪除。這樣得到新的假設集New_candidate_hypothesis。

⑥ 對New_candidate_hypothesis中的每個假設h，確定該條規則覆蓋樣本集S上的正例和負例數量，并由此計算它的TPR和FPR。如果假設h的TPR/FPR大于Best_hypothesis的TPR/FPR，則Best_hypothesis←h。

⑦ 選取New_candidate_hypothesis中TPR/FPR性能最好的k個規則來更新Candidate_hypotheses。

⑧ 如果Candidate_hypotheses=φ，返回到⑤。

⑨ 如果Best_hypothesis在樣本集S上的TPR/FPR≤(TPR/FPR)min，將該規則添加到規則集R中，并將它所覆蓋的SVs 從S中刪除，并轉到②。

⑩ 重復上述步驟②至⑨直到Stp中的所有SVs被覆蓋或者生成的規則因不滿足要求而被拒絕，規則生成算法終止。

3 實驗結果及分析

本節進一步對本文所提出的基于SVM-RFE特征提取的規則提取算法的性能進行了驗證。本算法是用MATLAB 7.8.0 (R2009b) 實現的，運行環境是一臺CPU 為 Intel Core 2-Quad processor，主頻2.8 GHz， 內存容量為4 GB的PC機，所用的SVM 軟件工具是較為流行的Libsvm (3.1.7)，其他對比的分類算法使用的是Weka 3.2相應的實現。

在實驗中我們主要用可理解性(comprehensibility)、正確率(accuracy)和忠實度(fidelity)等指標來進行評價。可理解性用規則的數量以及規則中前提條件平均項數來對其進行度量；正確率用被正確識別的樣本數占總樣本的比率來度量；忠實率用抽取的規則與支持向量機預測相一致的樣本數占總樣本的比率來表示。實驗主要采用了來自UCI庫的10個數據集，在所有的數據集上用于訓練和測試的數據比例為70:30，70%的數據通過10折交叉驗證法(10-folders cross validation)用來對分類器進行學習和提取規則，剩下的30%用于評估所產生的規則集的性能指標。

下面以Heart desease數據集為例進行說明，該數據集共有13個屬性和270個樣本，其中屬性1,4,5,8,10,12是連續值屬性，其他則為離散值屬性。在該數據集上隨機生成60個訓練和測試子集對，然后用SVM-FRE方法分別在這60個子集對上進行特征排序并確定其對應的最優特征子集，并按照式(2)對每一個屬性在這60個子集上的最優特征子集中出現的頻度和位置進行加權平均得到屬性排序列表，如表1所示。

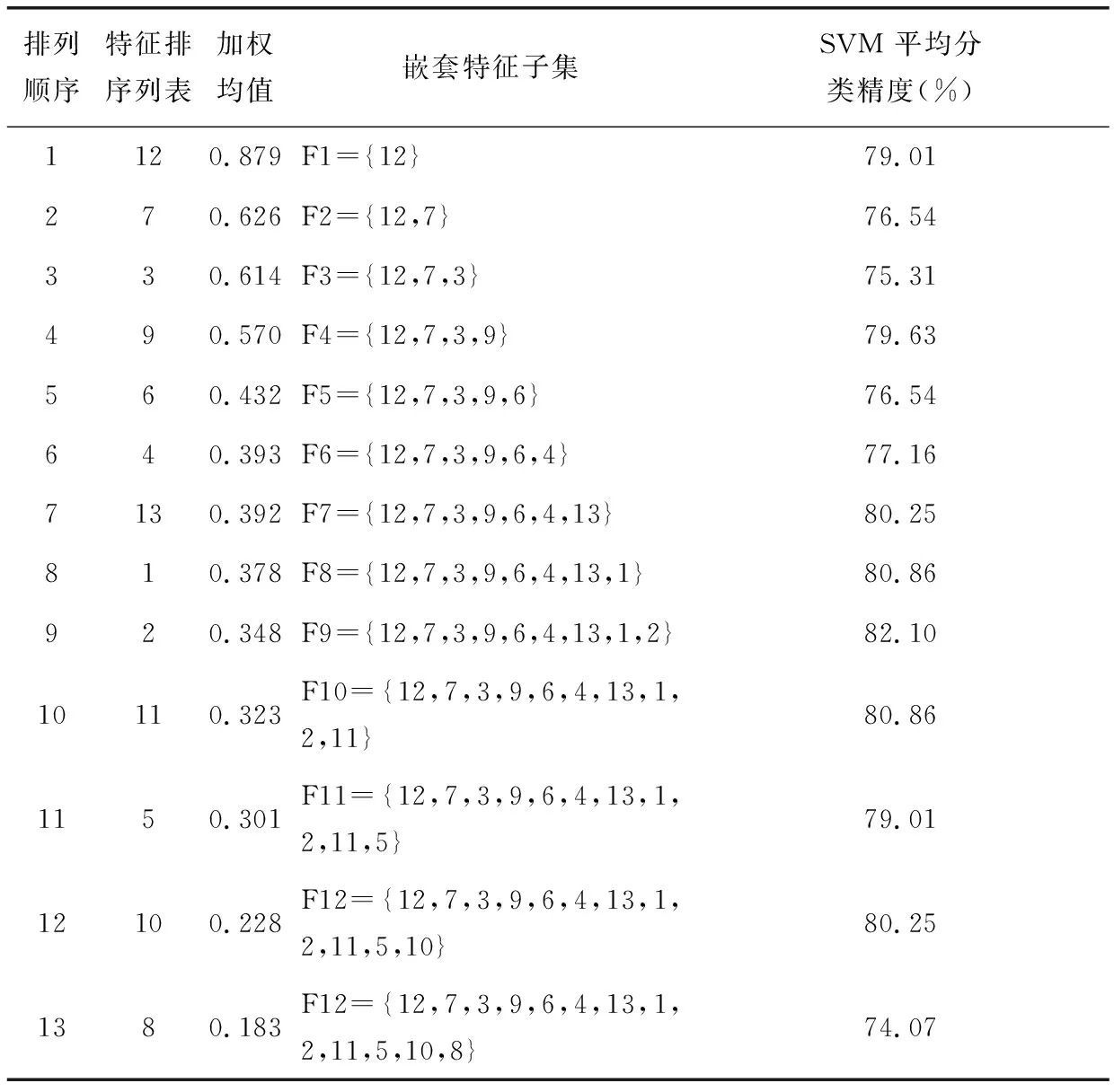
表1 Heart disease 數據的分析結果(分類器個數M3=60個)

將生成的嵌套特征子集在前面隨機產生的60個的測試集上計算SVM平均分類精度得到最優特征子集并最終得到最優特征子集{12,7,3,9,6,4,13,1,2}。用包含這些特征子集的數據集對SVM 進行訓練得到支持向量，并用生成的支持向量機模型對這些支持向量進行分類預測，去除預測分類結果與樣本原有的分類標簽兩者不一致的支持向量，得到清理后的支持向量。采用3.3節的方法生成5個規則(其中含1個默認規則)，我們分別計算每條規則增加前后的AUC的變化，如圖2所示。

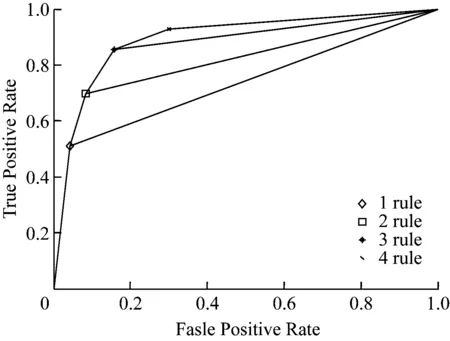
圖2 規則集在Heart desease 數據上的ROC圖

分別為：0.69，0.78，0.85，0.87。由于第4條規則增加后變化不顯著我們將其裁剪，得到規則集如式(5)。

R1：IFX13=7 ANDX3=4 THEN Occur=2

R2：IFX1≥59 ANDX9=1 THEN Occur=2

(5)

R3：IFX12=1 ANDX2=1 THEN Occur=2

Default: Occur=1

為了更好地對本文所提出的算法的性能進行評判，我們選取了兩個有代表性的規則提取方法，一個是直接從樣本中提取規則的C4.5算法，另一個是基于結構分析的SVM+ prototypes算法與本文提出的基于SVM-FRE特征選擇的規則提取方法進行比較。

這三種算法在5個數據集上的結果，如表2所示。

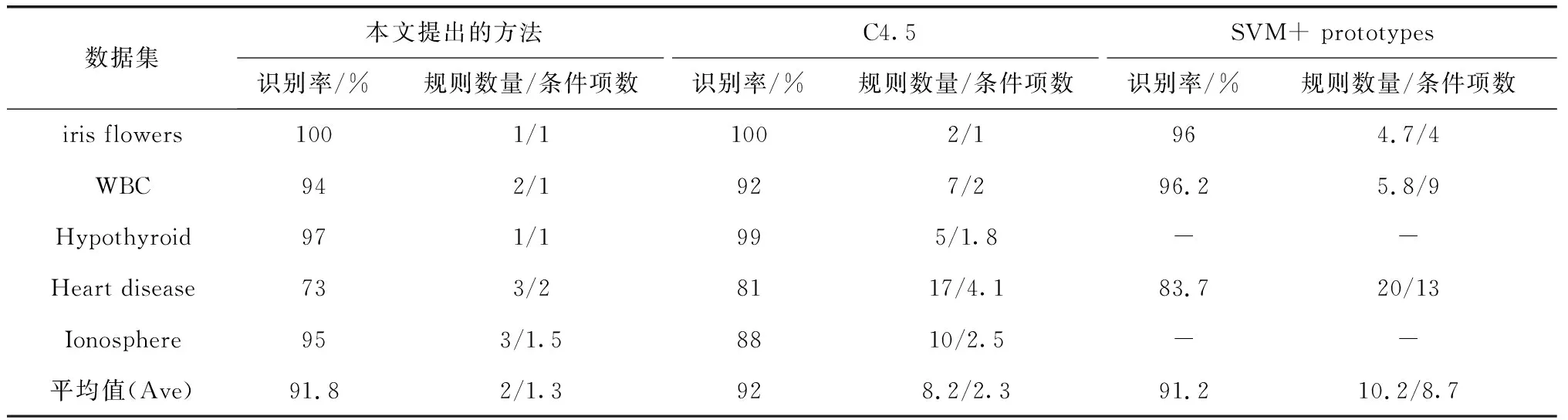
表2 本文提出的方法、C4.5算法和SVM+ prototypes算法的性能比較

從表中我們可以看出本文提出的算法在識別率上基本上和另外兩種相差不大，但所產生規則集中規則的數量以及規則前提中的條件明顯比另外兩種要小，提高了提取規則的可理解性。

4 總結

本文提出了基于SVM-RFE特征選擇的規則提取方法，該方法采用優化的SVM-RFE來獲取重要屬性集，并采用一種變型的順序覆蓋規則算法結合AUC進行規則生成和裁剪。實驗表明該方法在保持較高的精確度和忠實率的前提下提高了提取規則的可理解性。