電力供應量智能分析系統總體框架設計

杜俊賢

(煙臺汽車工程職業學院 電子工程系， 山東 煙臺 265500)

0 引言

電力系統在經濟發展中作用重大，迅速發展的經濟促使各產業的發展水平及國民生活水平得到快速提升，日常生產生活對用電量的需求隨之不斷提高，激增的用電量需求促使電力系統整體規模不斷擴大，一些新增發電項目在保障和促進經濟穩步發展中發揮著重要作用。為了促進電力系統的運行穩定性，必須要保證電網供需平衡。而目前調度計劃的制定需基于電力供應量及電力負荷的有效預測，準確的負荷預測是提升制定調度計劃準確度的重要手段，使由預測不準確帶來的棄電損失問題被有效避免。

1 需求分析

電力供應在日常生產生活中起到重要作用，隨著國民經濟發展對用電需求的不斷提升，對穩定的電力供應提出了更高的要求，仍然存在不同程度的供需矛盾，因此需對電力供求進行科學合理的規劃，并結合實際情況作出合理決策，促進經濟的穩定發展。基于統計學習理論的支持向量機屬于一種小樣本學習算法，分類與回歸分析的應用非常廣泛，支持向量機回歸因而在眾多領域(包括糧食產量、股市、氣象、電力負荷等方面的預測)得以廣泛應用。電力供應量的影響因素通常表現出較大的不確定性和復雜性，在統計電力產量時通常以季度或年作為時間標度，預測電力供應量屬于典型小樣本的非線性問題，但是支持向量機很難對樣本的特征屬性進行評價，所以在對模型進行訓練和檢驗過程中易受到一些次要屬性的干擾和影響，進而影響到最終的預測精度，因此對支持向量機的優化和完善仍然是研究重點，例如，通過對輸入樣本的權重或特征屬性進行優化處理，實現預測精準度的有效提高，在獲取樣本數據屬性的本質關系具有較大的優勢，對于知識的不確定性、信息的冗余程度具有較強的包容性，只要找到最小預測規則集即可[1]。因此本文在支持向量機回歸的基礎上結合運用粗糙集屬性約簡方法對數據樣本進行預處理和預測，針對電力相關歷史數據(包括產量及其主要影響因素)樣本建立回歸分析模型。

2 基于粗集屬性約簡的電力供應量智能預測

電網供需平衡是確保電力系統穩定運行的基礎，目前相關超大容量電能存儲技術仍處于研究階段，隨著用電需求和電力負荷的影響及制約因素的增加(如電價高低、區域經濟、氣候等關聯影響因素)，電力系統的穩定運行需通過相應發電調度計劃的有效實施實現，電力供應量及負荷預測在電力系統中起到非常重要的支持作用，電力規劃及日常生產運行等工作均離不開電力供應量及負荷預測(主要是對年最大負荷及用電量進行預測)，不斷增加的用電量對預測電力負荷的精準度提出了更高的要求，受到有限歷史數據的限制，電力負荷受不確定因素的影響較大，通過準確的電力負荷預測可以為社會效益的穩定發展提供保障。

2.1 支持向量機回歸應用原理

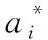
(1)

約束條件為式(2)。

(2)

針對非線性支持向量回歸問題，往往會將數據通過某一非線性映射的引入實現到更高維Hilbert空間的映射，線性回歸(對應原空間的非線性回歸)在此空間完成。為使高維空間內點積運算的復雜程度得到有效降低，針對低維空間輸入完成到高維特征空間的點積(通過核函數技術)，即K(xi，xj)=<Φ(xi)，Φ(xj)>。

對于非線性回歸，其最優超平面解析的表達式[2],如式(3)。

(3)

常用核函數包括p階多項式核函數 、高斯徑向基核函數、Sigmoid核函數，對應表達式如式(4)—式(6)。

K(xi，xj)=(<(xi，xj>+c)p(p∈N，c≥0)

(4)

K(xi，xj)=exp {-‖xi，xj‖2/2σ2}

(5)

K(xi，xj)=tanh(θ+υ)

(6)

2.2 粗集和屬性集相對約簡在電力供應量智能預測中的應用

實際在對樣本數據采用粗集理論進行分析時，通常以決策表作為處理對象。

(1) 決策表的定義：由知識表達系統構成決策表，其信息表具體由四元組構成表達式為S=(U，A，V，f)，U(非空有限對象集) 表示論域；V的集合由屬性a∈A的值域構成;A(非空有限屬性集)取值為C∪D;C表示條件屬性集;D(非空集) 表示決策屬性集;f表示信息函數各對象在指定論域U中各屬性的取值(U×A→V)。在D僅有一個決策屬性g0gggggg的情況下則為單一決策表。

(2) 上 、下近似集的定義：對任意XU及其上由B表示的等價關系，X在此關系下的上 、下近似集定義表達式如式(7)、式(8)。

B-(X)={x|x∈U∧ [x]B∩X≠?}

(7)

B-(X)={x|x∈U∧ [x]B?X}

(8)

X在B-(X)同B-(X)取值不同的情況下稱為一個B粗集。

(3) 正域的定義：由P、Q表示U上的兩個等價關系，定義Q的P正域表達式如式(9)(即以U|P的信息為依據能夠完成到Q的等價類中開集的集合的準確劃分)。

POSP(Q)=UX∈U|QP-(X)

(9)

(4) 約簡的定義：設論域U上的兩個等價關系簇由P、Q表示，?r∈S、POSS(Q) =POSP(Q)且POSS /{r}(Q) 同POSS(Q)的取值不同則S?P是P的Q獨立子集，滿足S是P的Q約簡的條件[2]。

各屬性在決策表信息系統中均與某個等價關系相對應，對于論域樣本上的論域通過使用條件屬性集和決策屬性集完成劃分及對應分類知識 的形成，對于條件屬性集則通過運用屬性約簡實現部分必要屬性的獲取，這部分必要屬性的分類能力不同于決策屬性同全部條件屬性相同。假設，S=(U，A，V，f)表示決策表;U表示論域取值為{x1，x2， …，xn}；A=C∪ g0gggggg，[ mina，maxa]表示屬性a(aA是一個連續屬性) 的值域。粗集理論的處理對象適用于離散屬性，在決策表含有連續屬性的情況下需進行離散化處理，本文使用凝聚層次聚類法完成離散化處理過程使負荷預測的精準度得到顯著提高，根據定義(4)完成C(條件屬性集合) 的約簡的獲取，由Cred表示C的相對約簡即C的最大獨立子集(相對于決策屬性g0gggggg)[3]。

3 電力供應量數據準備與預處理

電力供應量會受到生活水平、經濟水平等多種因素的影響，本文選擇電力產量(億千瓦小時)、國內生產總值(億元)、第一產業、第二產業、第三產業(億元)、人均國內生產總值(元 / 人)、原油產量、生鐵 產量、鐵路貨運量(萬噸)、原煤產量(億噸)因素作為代表，分別由d、a1、a2、a3、a4、a5、a6、a7、a8、a9表示[4]。

根據實際需要選取某一時間段的電力供應量的歷史數據進行處理，主要步驟如下。

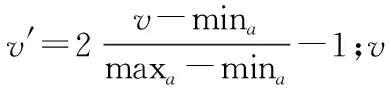
4 支持向量機回歸結果與分析

通用MATLABSVMToolbox的使用完成對支持向量機回歸的處理過程，核函數為K(xi，xj)=exp{-‖xi，xj‖2/2σ2}； 以線性ε-insensitive 函數作為損失函數，表達式為L(f(x)，y)=max(0， |f(x)-y|-ε)[6]。通過交叉驗證確定參數C，σ，ε的選擇。將原樣本上述步驟(4)和(5)進行處理以便后續比較。兩種回歸的相關參數和結果,如表1—表3所示。

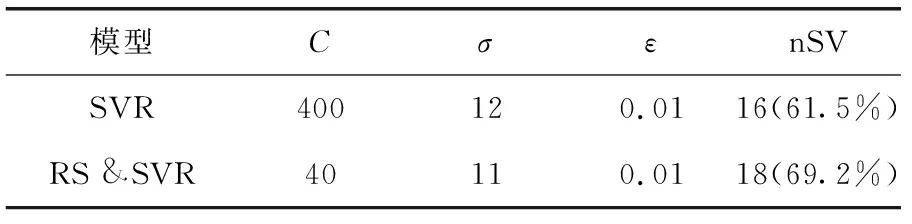
表1 參數值和支持向量個數

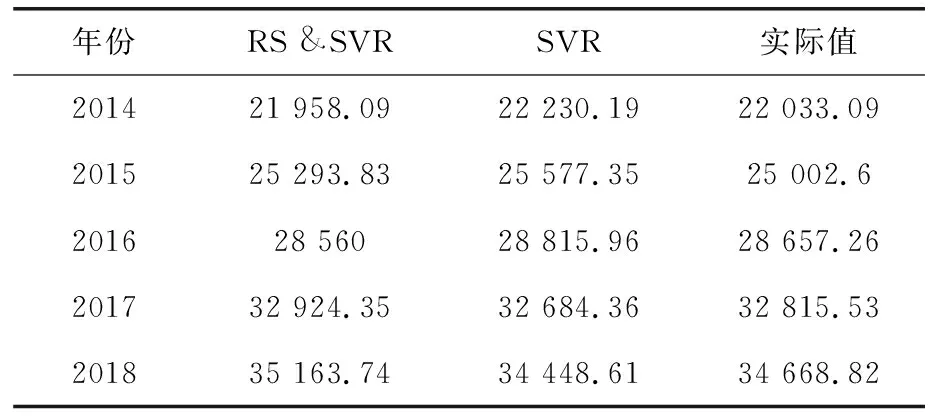
表2 電力產量預測值與實際值

表3 模型預測精度比較

其中,RMSE為式(10)。

(10)

THEIL_IC為式(11)。

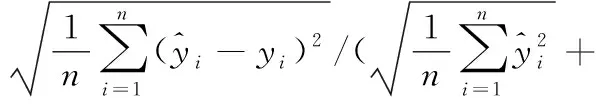
(11)

取值范圍通常在 0—1之間的希爾不等系數同預測精度成反比，即希爾不等系數越小精度越高，如式(12)。

(12)

通常在MAPE的值不超過10 的情況下表示預測精度較高，如式(13)。

(13)

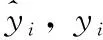
本文的RS &SVR 模型在支持向量個數方面類似于SVR模型，僅多了兩個支持向量。由表2—表3可知， RS &SVR 模型的希爾不等系數以及均方根誤差更小，預測值更加接近實際值，說明擬合效果及預測效果良好，充分證明了本文所構建模型應用于電力供應量回歸預測過程的有效性，在滿足用電需求、降低發電成本及確保電網安全穩定運行中具有較高的實用性[7]。

5 總結

在對電力供應量進行分析過程中采用支持向量機回歸能夠構建起較為理想的預測模型，而在對不確定的、冗余的信息進行處理時粗糙集理論表現出了強大的優勢，通過在數據預處理過程中使用屬性約簡方法可使電力相關數據樣本的特征維得到有效簡化。結合運用支持向量機回歸同粗糙集理論間構建的RS&SVR模型使電力供應量智能預測效果得到顯著提升，使用屬性約簡算法完成約簡處理，將電力供應量的預測結果同實際情況進行實驗對比，本文基于屬性約簡方法構建的預測模型能夠對較少的主要預測因子的信息進行充分利用， 預測結果的精準度得到顯著提高。