信息系統運行的穩定狀態計算方法

張銀鐵, 王麗君, 萬晶

(國網電力科學研究有限公司 信息系統集成分公司， 江蘇 南京 211106)

0 引言

信息系統在運行過程中，各種運行指標一定是隨著使用人員、時間階段、業務變化而變化的，運維過程中最大的難點就是無法準確掌握運行的歷史規律，指標高低并不能直接說明系統運行是否穩定。在運行監控中常見的監控辦法是設置監控閥值，但是監控閥值是很難設定的，指標高并不能說明系統運行就一定有問題，指標低也不能說明系統運行沒有問題。最合理的辦法是計算出系統在不同時間階段的穩定運行狀態，動態判斷每一時刻與穩定狀態的差異，進而掌握系統穩定之間的差異。

1 歷史數據中的規律

1.1 歷史數據使用誤區[1]

在信息系統運行過程中，需要監控的指標是非常多的，包括CPU、內存、磁盤、網絡等多個類別，每一個類別又可以細分為多個二級、三級等子類，例如CPU的運行狀態既有總負載情況，也有分core負載狀態，每一個狀態又可以再細分為sys負載、user負載和IO等待等。監控數據是隨著時間進行記錄的，這些歷史數據是監控閥值設定的基礎，比如CPU負載過高時容易造成宕機，所以設置閥值在90%等，預留處置時間。常見的閥值設置是通過歷史數據判斷最高狀態，當最高狀態都不超過80%，設置閥值為90%就并不合理了。

常見的解決辦法有兩種，一是極值判斷，二是方差分析。

(1) 機制判斷的問題

取歷史一定周期的監控數據，例如CPU狀態每分鐘記錄一個監控狀態，就有一天1 440個指標，一周就有10 080個指標，計算其中指標的最高值、最低值，超過最高或低于最低都是閥值的判斷標準。這種判斷最大的問題是系統運行是有實際差異的，白天的狀態一定高于夜間，工作日狀態一般也是高于非工作日狀態的，特殊調度時負載也會明顯高于普通狀態的，極限狀態并不能說明極限范圍內就一定沒有問題，并不能說明系統在區間范圍內就是穩定的。

(2) 方差分析的問題

方差分析法是將上述指標進行統計計算，尋找到99%指標所處的區間，為了加強監控力度，甚至可以尋找到95%指標所在的區間作為監控閥值，可以一定程度上解決極限判斷的問題。但是方差分析也存在一個問題，系統運行本身是不可能按照一個固定模式進行得分，負載都是動態變化的，或持續在增長、或持續有下降，樣本中原本較低的數值也并不一定就是有問題的，是系統狀態動態變化的過程，例如系統用戶在持續增加，一段時間的前后負載都是正常的，高低之差并不能說明系統存在問題。

1.2 理論中的穩定狀態[2]

通過上述分析可知，判斷出系統的穩定狀態才能準確地掌握動態閥值的設置條件，可以參考數據集中度進行判斷。在數據統計中常見的方法是通過平均值反應數據的集中程度。但是平均值也是有問題的，每天的1 440個分鐘指標是不能區分不同時刻業務差異的，需要的是判斷計算周期內每一個時刻的穩定狀態，例如每天8:00這個時刻在過去一個月的監控記錄，計算出8:00這個時刻如果正常的理論穩定指標值，這個值可能是平均值也可能不是平均值。因此，假設一種系統在每一個時刻都存在一個穩定狀態值，這個值可以使每一天這個時刻的運行值都是圍繞這個穩定運行狀態在運行的，即穩定狀態值與每天同一個時刻樣本中所有指標之間的差值之和是最小的，如式(1)。

(1)

其中，f(x)表示樣本同時刻每一個值與理論穩定值之間的差值之和；x表示樣本中種同時刻每一個時刻的監控歷史記錄值；X表示同時刻x樣本的平均值；a表示修正平均值的修正值，即X+a是計算時刻歷史記錄中理論穩定運行的狀態值；n表示樣本中這個時刻的數據量，即為計算的樣本歷史天數。

通過絕對值函數特性可知，f(x)是一個隨著x不斷變化的值，并且是一個始終大于零的數值，通過導函數可知f(x)存在最小值,如圖1所示。

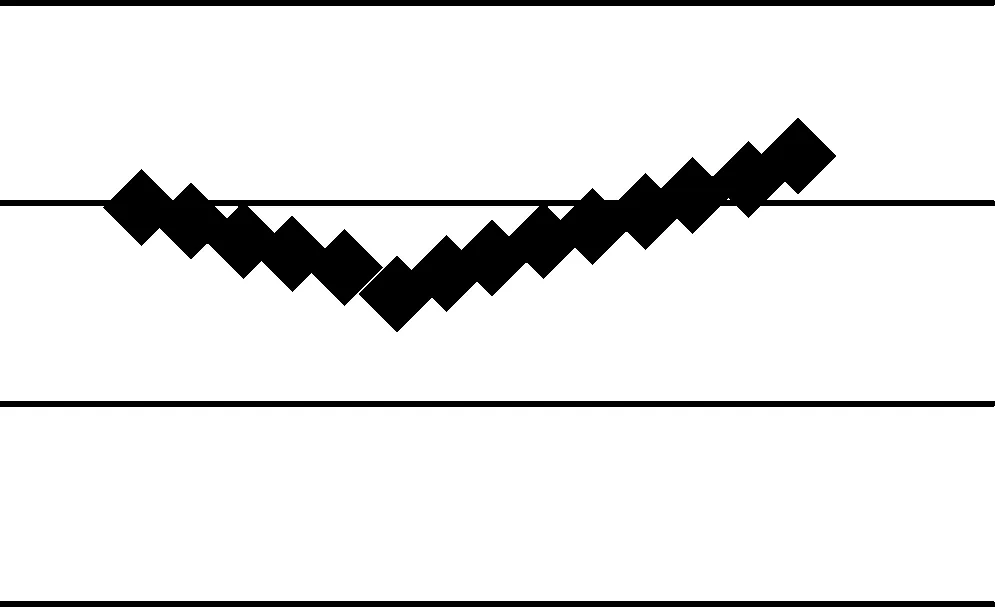
圖1 趨勢判斷示意

樣本值x都是已知的，而修正值a是不確定的，因此將f(x)自變量變為a，即可計算得出修正值a在某數值時，可以使得f(x)最小，計算每一指標、每一時刻在樣本周期中的理論穩定狀態,如式(2)。

(2)

其中，f(x)表示樣本中每一個值與理論穩定值之間的距離和；x表示修正平均值的穩定修正值，即X+x是計算時刻歷史記錄中理論穩定運行的狀態值；xi表示樣本中每一個時刻的監控歷史記錄值；X表示xi樣本的平均值；n表示樣本中這個時刻的數據量，即為計算的樣本歷史天數。

2 穩定狀態計算方法

2.1 公式轉換

通過上述分析可知存在一個修正平均值的值，可以得到某時刻的理論穩定運行狀態，這個時刻的所有監控記錄都應該圍繞這個值在運行，也是一種反應樣本集中度的數值，只不過不是平均值等常見統計數值，是一種修正后的數值。因為上述函數是一個絕對值函數，并且固定參數是隨著樣本不斷變化的，因此將上述函數進行格式轉換，便于進行絕對值判斷[3-5],如式(3)、式(4)。

(3)

(4)

因為xi和X在樣本確定的情況下都是固定值，所以將xi-X記作xi，得到式(5)。

(5)

其中，f(x)表示需要得到最小值；x表示f(x)最小時的x變量；xi表示樣本確定后的固定參數。將公式轉換為求得絕對值函數最小時的x值，如式(6)。

f(x)=|x-x1|+|x-x2|+…+|x-xn|

(6)

2.2 計算判斷[6-7]

轉換后的公式可知f(x)最小狀態與n的數值是有關聯關系的，因此區分兩種情況分別計算判斷。

(1)n=2k時

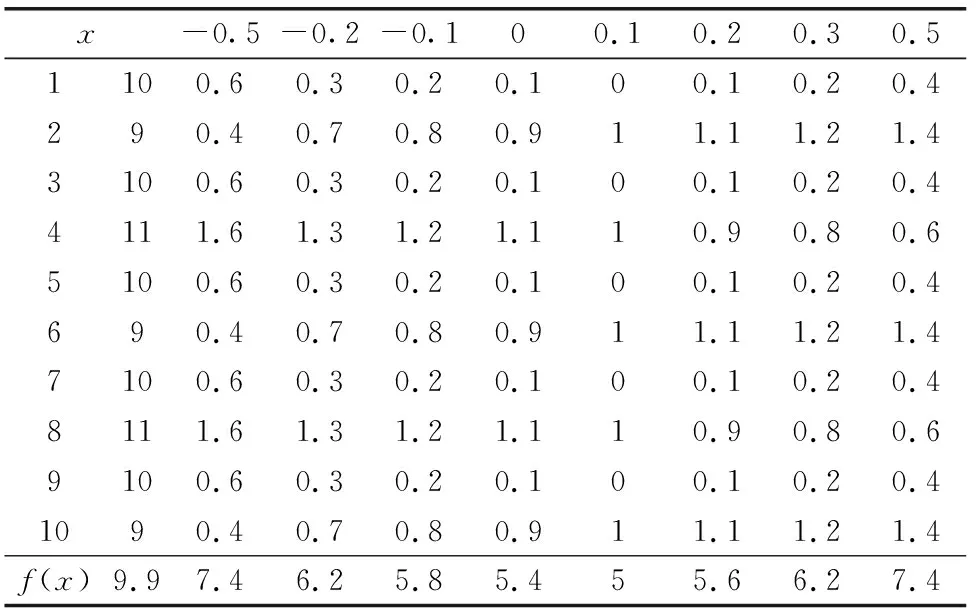
設ak

|x-a1|+|x-a2k|≥a2k-a1

(7)

當且僅當x∈(a1,a2k)等號成立,如式(8)。

|x-a2|+|x-a2k-1|≥a2k-1-a2

(8)

當且僅當x∈(a2,a2k-1)等號成立，依次類推得到式(9)。

|x-ak|+|x-ak+1|≥ak+1-ak

(9)

當且僅當x∈(ak,ak+1)成立，(ak,ak+1)是各組合區間的共有子區間，所以當x∈(ak,ak+1)時，各等號成立，才能使f(x)達到最小值。

(2)n=2k-1時,有式(10)。

|x-a1|+|x-a2k-1|≥a2k-1-a1

(10)

當且僅當x∈(a1,a2k-1)成立,有式(11)。

|x-a2|+|x-a2k-2|≥a2k-2-a2

(11)

當且僅當x∈(a2,a2k-2)成立，依次類推得到|x-ak|≥0,當且僅當x=ak時等號成立，x=ak是以上各區間的公共元素，所以此時f(x)達到最小值。

(3) 計算結論,如式(12)。

(12)

求x為多少時，f(x)最小，即此時修正值可以修正平均值，得到系統運行指標的理論穩定狀態。

當n=2k時，x∈(xk,xk+1)，f(x)最小。

當n=2k-1時，x=xk，f(x)最小。

2.3 數據驗證

假定某時刻監控指標是一個圍繞10數值上下浮動的，即10是理論上穩定的運行狀態，從兩個方面驗證上述穩定狀態修正值的計算合理性。分為兩個維度驗證，一是數據不存在異常數據，是否可以得到穩定修正值，二是數據存在異常數據，驗證是否可以得到穩定修正值[8-10]。

(1) 無異常數據的驗證

隨機樣本值為(10,9,10,11,10,9,10,11,10,9),得到驗證數據表,如表1所示。

表1 無異常驗證數據

由表1可知，樣本平均值為9.9，當x=0.1時f(x)得到最小值5，即9.9+0.1=10，可以修正得到穩定狀態值。

(2) 有異常數據的驗證

隨機樣本值為(10,9,10,11,18,9,10,11,10,9)，其中18是樣本中的異常數據，得到驗證數據表如表2所示。

表2 有異常驗證數據

由表2可知，樣本平均值為10.888 9，當x=-0.9時f(x)得到最小值12.055 56，即10.888 89-0.9=10，可以修正得到穩定狀態值，穩定狀態計算方法可以剔除出樣本中的異常數值。

3 穩定狀態使用技巧

首先，通過信息系統運行的穩定狀態計算方法可以知曉，這個穩定的狀態只是一個理論中的穩定狀態，信息系統運行是不存在絕對穩定的，因此穩定狀態只是用來判斷樣本中其他數據偏離情況的一個參考，偏離的多可以說明此時刻這個樣本是存在異常的，是需要重點進行排查，但不能說是存在故障。

其次，穩定狀態計算方法受限于樣本的數量，奇偶數量下是存在一定誤差可能的，只有樣本數量足夠大才能保障穩定狀態的可信度不斷提升，這又與某一時刻樣本的數量限制產生矛盾，畢竟同一時刻的樣本值一年也只有365個，如果一年中發生系統大的檢修，還要對樣本進行分組，所以穩定狀態只是理論值，是用來輔助判斷集中趨勢的參考，是動態閥值的參考。

最后，系統如果不存在穩定狀態，例如是一種持續增長負載的狀態，則計算得出的理論穩定值也只是這一個變化過程的中間狀態，這時就需要將樣本進行分組處理，檢查穩定狀態的變化情況，即可判斷系統的變化趨勢。

4 總結

信息系統的運行如同人體的各項生理指標，例如血常規等指標項，都需要一個明確的正常穩定狀態值，輔助人員或人工智能判斷指標與穩定狀態的偏離情況，才能動態準確地掌握系統的歷史規律，不同系統不同指標通過歷史數據都可以得到私有的穩定狀態值，但是這種穩定狀態只是理論狀態，只是輔助判斷時進行動態監控的參考，不應該作為絕對的監控閥值使用。