新能源化工熱力學(xué)
練成,程錦,黃盼,陶浩蘭,楊潔,劉洪來,3
(1 華東理工大學(xué)化學(xué)與分子工程學(xué)院,上海 200237;2 化學(xué)工程聯(lián)合國(guó)家重點(diǎn)實(shí)驗(yàn)室,上海 200237;3 華東理工大學(xué)化工學(xué)院,上海 200237)
能源存儲(chǔ)與轉(zhuǎn)換是目前人類能源相關(guān)技術(shù)中的重要課題,主要涉及電化學(xué)過程,因?yàn)殡娛且环N品位很高的能量,可以通過其他形式能源與電能的互相轉(zhuǎn)換來高效地利用能量,在一定程度上解決能源問題。電化學(xué)是研究?jī)深悓?dǎo)體(電子導(dǎo)體,如金屬或半導(dǎo)體;離子導(dǎo)體,如電解質(zhì)溶液)形成的接界面上所發(fā)生的帶電及電子轉(zhuǎn)移變化的科學(xué),主要涉及能量的儲(chǔ)存、釋放和轉(zhuǎn)化過程。其高速發(fā)展離不開熱力學(xué)的研究指導(dǎo)。
熱力學(xué)主要分為兩大部分:一個(gè)部分為實(shí)驗(yàn)方面對(duì)物質(zhì)熱力學(xué)性質(zhì)的研究與熱力學(xué)數(shù)據(jù)的測(cè)定;另一個(gè)部分為理論計(jì)算方面對(duì)物質(zhì)性質(zhì)的模擬與預(yù)測(cè),從理論的角度闡明物質(zhì)能量轉(zhuǎn)換和狀態(tài)變化的規(guī)律。兩個(gè)部分相輔相成,各有所長(zhǎng)。實(shí)驗(yàn)是一切化學(xué)研究的基礎(chǔ),可以得到所需體系準(zhǔn)確的熱力學(xué)參數(shù),而理論研究則在實(shí)驗(yàn)的基礎(chǔ)上探索規(guī)律與原理。實(shí)驗(yàn)研究雖然十分重要,但卻有多種限制因素,例如人們不可能測(cè)定所有體系的所有熱力學(xué)性質(zhì),也難以對(duì)微觀的體系進(jìn)行實(shí)驗(yàn)研究。而理論研究則可以通過計(jì)算快速對(duì)所需研究體系的性質(zhì)進(jìn)行預(yù)測(cè),也可以通過已知的理論工具去探索實(shí)驗(yàn)所無法涉及的領(lǐng)域,如納米尺度的粒子行為、電子結(jié)構(gòu)對(duì)體系的影響。因此,本文主要從理論計(jì)算方法的角度介紹熱力學(xué)在電化學(xué)能源存儲(chǔ)與轉(zhuǎn)換的應(yīng)用。化工熱力學(xué)通過對(duì)電化學(xué)過程、材料、工藝的研究以及計(jì)算機(jī)技術(shù)的輔助,可以快速且定量地解決大量關(guān)鍵問題。除了傳統(tǒng)的經(jīng)典熱力學(xué)以外,近年來分子與統(tǒng)計(jì)熱力學(xué)也有著蓬勃發(fā)展,而今的研究已經(jīng)更關(guān)注非平衡態(tài)熱力學(xué)過程。最后,計(jì)算機(jī)技術(shù)的發(fā)展也為熱力學(xué)研究帶來了高通量計(jì)算與機(jī)器學(xué)習(xí)的方法。綜上所述,熱力學(xué)研究大幅度提高了電化學(xué)領(lǐng)域的發(fā)展速度。
本文整理、分析了理論計(jì)算方面熱力學(xué)在電化學(xué)能源存儲(chǔ)與轉(zhuǎn)換領(lǐng)域的相關(guān)重要理論與最新研究成果。對(duì)不同熱力學(xué)理論方法的研究進(jìn)行分類和介紹,并針對(duì)其中分支的經(jīng)典熱力學(xué)、統(tǒng)計(jì)熱力學(xué)、非平衡態(tài)熱力學(xué)、機(jī)器學(xué)習(xí)等關(guān)鍵領(lǐng)域進(jìn)行了詳細(xì)探討,在文末分析了今后發(fā)展中應(yīng)重點(diǎn)思考和解決的問題,以期為電化學(xué)中熱力學(xué)的進(jìn)一步研究與電化學(xué)行業(yè)的進(jìn)步提供參考與啟發(fā)。
1 電化學(xué)的經(jīng)典熱力學(xué)
1.1 經(jīng)典熱力學(xué)概述
熱力學(xué)在形成初期只是研究熱能與機(jī)械能間的轉(zhuǎn)換,后來逐漸發(fā)展為研究與熱現(xiàn)象有關(guān)的各種能量轉(zhuǎn)換和狀態(tài)變化的規(guī)律。經(jīng)典熱力學(xué)研究?jī)?nèi)容主要以熱力學(xué)三個(gè)定律為基礎(chǔ),利用熱力學(xué)數(shù)據(jù),研究平衡系統(tǒng)各宏觀性質(zhì)之間的相互關(guān)系,揭示變化過程的方向和限度,結(jié)論具有普遍性。但是它不涉及粒子的微觀性質(zhì),不能闡明體系性質(zhì)的內(nèi)在原因,不能給出微觀性質(zhì)與宏觀性質(zhì)之間的聯(lián)系,不能對(duì)熱力學(xué)性質(zhì)進(jìn)行直接的計(jì)算。要克服這些缺點(diǎn)必須從分子的微觀結(jié)構(gòu)和內(nèi)部運(yùn)動(dòng)去認(rèn)識(shí)體系及其變化。
經(jīng)典熱力學(xué)對(duì)電化學(xué)的研究也主要集中在宏觀性質(zhì)方面。隨著電化學(xué)工業(yè)規(guī)模的擴(kuò)大、新過程的開發(fā)以及計(jì)算機(jī)的使用,經(jīng)典化工熱力學(xué)的研究和應(yīng)用也有了較大的發(fā)展。
1.2 經(jīng)典熱力學(xué)在電化學(xué)能源存儲(chǔ)與轉(zhuǎn)換領(lǐng)域的應(yīng)用
電能是一種經(jīng)濟(jì)、實(shí)用、清潔且容易控制和轉(zhuǎn)換的能源形態(tài),如何將其他類型的能源(風(fēng)能、潮汐能、太陽能等)轉(zhuǎn)化成電能并存儲(chǔ),這一過程與電化學(xué)息息相關(guān)。傳統(tǒng)電化學(xué)主要研究電能和化學(xué)能之間的相互轉(zhuǎn)換,如電解池和原電池。
經(jīng)典熱力學(xué)主要解決宏觀的穩(wěn)態(tài)問題,對(duì)于宏觀電化學(xué)過程與液態(tài)電解質(zhì)溶液的描述已經(jīng)有了成熟的研究。本節(jié)將著重于介紹三個(gè)方面的熱力學(xué)研究:電化學(xué)過程、電解質(zhì)溶液、電解質(zhì)溶液的過量函數(shù)(活度系數(shù))模型。
1.2.1 電化學(xué)過程的熱力學(xué)
從形式上來說,電化學(xué)過程與一般化學(xué)反應(yīng)的區(qū)別在于:反應(yīng)在電極的表面上進(jìn)行,溶液中有離子的遷移,并有電能的輸入和輸出。從熱力學(xué)原理分析,最顯著的特征是各相電位不同,過程進(jìn)行時(shí)不僅做體積功,還伴隨電功。
一般恒溫恒壓下的化學(xué)反應(yīng)只涉及體積功,dGT,p,dW′=0≤0,其中G 為吉布斯自由能,反應(yīng)中吉氏函數(shù)必定減少。
(1)兩種電化學(xué)過程 在電化學(xué)過程中,系統(tǒng)對(duì)外輸出電功或環(huán)境對(duì)系統(tǒng)輸入電功,采用ΔGT,p≤W′ele,根據(jù)ΔGT,p大于零還是小于零,可分為兩類。
(a)ΔGT,p< 0的過程,這類過程可以對(duì)外輸出電 功, W′ele< 0, W 為 電 功, 最 大 可 輸 出W′ele= ΔGT,p。這種電化學(xué)過程是化學(xué)電源的基本過程。
(b)ΔGT,p> 0的過程,這類過程必須得到電功才能進(jìn)行,W′ele> 0,最少應(yīng)得W′ele= ΔGT,p。這種電化學(xué)過程是電解和電冶煉工業(yè)的基本過程。氯堿、電解鋁、電解鎂等工業(yè)的基本過程都是ΔGT,p> 0的過程。
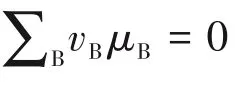
(3)電池的電動(dòng)勢(shì) 電池建立后,各相即存在一定的電位,界面兩邊就有一定的電位差。當(dāng)沒有外接負(fù)載,在開路下進(jìn)行一微元過程時(shí),電動(dòng)勢(shì)就是開路下電池中界面電位差的代數(shù)和。
不論是化學(xué)電源還是電解,當(dāng)外加電壓與電動(dòng)勢(shì)絕對(duì)值相等,但方向相反時(shí),所進(jìn)行的電化學(xué)過程為可逆過程。

最后,介紹電化學(xué)過程的有效能。電功可以任意地轉(zhuǎn)換,是品位最高的能量,因此電功即可定義為有效能。過程熱力學(xué)分析原理不變[1]。
1.2.2 電解質(zhì)溶液的熱力學(xué)性質(zhì)
電解質(zhì)溶液的最大特點(diǎn)是溶液中不僅存在分子,如溶劑分子和未離解的電解質(zhì)分子,還存在由電解質(zhì)離解產(chǎn)生的帶正電荷或負(fù)電荷的離子。根據(jù)電解質(zhì)在溶劑中的離解能力,理論上可分為兩大類電解質(zhì)溶液。第一類電解質(zhì)溶液中的電解質(zhì)是完全離解的,沒有未離解分子或正負(fù)離子締合物,如堿金屬、堿土金屬、過渡金屬的鹵化物以及一些過氯酸鹽的水溶液。第二類電解質(zhì)溶液中的電解質(zhì)則是部分離解的,溶液中有未離解的、原子間按共價(jià)鍵形式結(jié)合的分子,如各種強(qiáng)酸和弱酸、弱堿的水溶液;或有正負(fù)離子締合形成的離子對(duì),如二價(jià)金屬的硫酸鹽以及一些強(qiáng)堿的水溶液等。

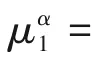

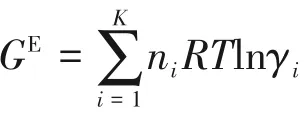
經(jīng)典熱力學(xué)方法,還可得到其他過量函數(shù)。
1.2.3 電解質(zhì)溶液的過量函數(shù)(活度系數(shù))模型
隨著現(xiàn)代統(tǒng)計(jì)力學(xué)理論在電解質(zhì)溶液中的應(yīng)用,電解質(zhì)溶液理論取得了長(zhǎng)足發(fā)展,建立了多個(gè)在工程計(jì)算上有廣泛應(yīng)用的模型[1-6]。
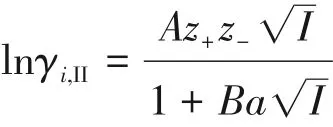
(2)Pitzer 模型 Pitzer 將離子處理為帶電硬球,并引入經(jīng)驗(yàn)的維里展開,以計(jì)及非靜電相互作用。各種電解質(zhì)的參數(shù)已被列出[2-3]。參數(shù)與溫度關(guān)系[7-8]已被研究,可用于混合電解質(zhì)溶液[9]。陸小華、王延儒和時(shí)鈞等[10-12]對(duì)Pitzer 參數(shù)以及對(duì)混合溶劑的推廣進(jìn)行了深入研究。
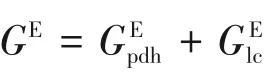
(4)電解質(zhì)溶液的積分方程理論和微擾理論 電解質(zhì)溶液模型的最新發(fā)展主要是在統(tǒng)計(jì)力學(xué)的積分方程理論和微擾理論的基礎(chǔ)上發(fā)展實(shí)用的工程計(jì)算模型,多數(shù)是在Blum的平均球近似(MSA)結(jié)果的基礎(chǔ)上研究電解質(zhì)溶液。
Blum采用MSA簡(jiǎn)化OZ積分方程中的離子間直接相關(guān)函數(shù)與離子間位能函數(shù)的關(guān)系,對(duì)具有不同大小和不同電荷的帶電硬球混合物(原始模型)獲得了解析式。其過量亥氏函數(shù)可表達(dá)為離子間硬球排斥作用的貢獻(xiàn)和離子間靜電相互作用的貢獻(xiàn)兩項(xiàng)之和。硬球排斥作用的貢獻(xiàn)采用Mansoori-Carnahan-Starling-Leland[20-21]狀態(tài)方程計(jì)算。離子間靜電作用的貢獻(xiàn)由Blum[22]的MSA 計(jì)算。在Blum的MSA 理論基礎(chǔ)上可以進(jìn)一步考慮離子間的其他相互作用,從而改進(jìn)模型的計(jì)算精度[23-25]。
2 電化學(xué)的分子和統(tǒng)計(jì)熱力學(xué)
2.1 分子和統(tǒng)計(jì)熱力學(xué)概述
分子和統(tǒng)計(jì)熱力學(xué)是在經(jīng)典熱力學(xué)與統(tǒng)計(jì)物理學(xué)的基礎(chǔ)上發(fā)展起來的。在經(jīng)典熱力學(xué)領(lǐng)域,人們已經(jīng)可以解決大部分宏觀問題,但是由于經(jīng)典理論的局限性,無法解決一些微觀的、復(fù)雜的體系。為了解決這個(gè)問題,逐漸發(fā)展了分子和統(tǒng)計(jì)熱力學(xué)。分子熱力學(xué)在分子水平上研究工程或應(yīng)用中出現(xiàn)的熱力學(xué)問題,起源于玻爾茲曼等從分子間相互作用力的角度出發(fā)對(duì)統(tǒng)計(jì)熱力學(xué)的研究,其主要內(nèi)容是提供表達(dá)分子結(jié)構(gòu)的分子參數(shù)與熱力學(xué)性質(zhì)間的定量關(guān)系。分子和統(tǒng)計(jì)熱力學(xué)在經(jīng)典熱力學(xué)的基礎(chǔ)上,開始關(guān)注單個(gè)粒子的貢獻(xiàn)與分布,在理論上引入了與粒子位置(r)有關(guān)的函數(shù),也開始考慮了量子化學(xué)中電子的影響。分子和統(tǒng)計(jì)熱力學(xué)在長(zhǎng)期發(fā)展中,主要誕生了以下強(qiáng)有力的研究工具:基于量子力學(xué)的密度泛函理論(QDFT)、經(jīng)典密度泛函理論(CDFT)、聯(lián)合密度泛函(Joint DFT)、基于反應(yīng)力場(chǎng)的分子動(dòng)力學(xué)(ReaxFF MD)和從頭算分子動(dòng)力學(xué)(AIMD)。分子和統(tǒng)計(jì)熱力學(xué)將人們探索熱力學(xué)的領(lǐng)域又一次拓寬了。
2.2 分子和統(tǒng)計(jì)熱力學(xué)在電化學(xué)能源存儲(chǔ)與轉(zhuǎn)換領(lǐng)域的應(yīng)用
電化學(xué)的發(fā)展中誕生了許多新的問題,經(jīng)典熱力學(xué)已經(jīng)無力解決,需要新的方法、新的思路來進(jìn)行突破。分子和統(tǒng)計(jì)熱力學(xué)的理論在過去幾十年里已經(jīng)突飛猛進(jìn),在電化學(xué)能源存儲(chǔ)與轉(zhuǎn)換領(lǐng)域可以解決大量問題,但以穩(wěn)態(tài)為主,下文主要介紹五個(gè)分子和統(tǒng)計(jì)熱力學(xué)理論方法及其所解決的問題:①量子力學(xué)的密度泛函理論(QDFT),可以研究某些難以解釋的實(shí)驗(yàn)現(xiàn)象及其相關(guān)機(jī)理;②經(jīng)典密度泛函理論(CDFT),探究粒子在帶電表面(孔道)、受限空間中的分布;③聯(lián)合密度泛函理論(JDFT),自洽高效地解決復(fù)雜固液表界面問題;④分子動(dòng)力學(xué)(MD),可以分析機(jī)理、篩選材料,還可以獲得原子的動(dòng)力學(xué)軌跡來研究擴(kuò)散機(jī)制等。
2.2.1 量子力學(xué)的密度泛函理論(QDFT)
隨著科技的發(fā)展,大量的新型材料應(yīng)需而生,而在應(yīng)用過程中某些實(shí)驗(yàn)現(xiàn)象難以解釋及其相關(guān)機(jī)理尚不明確[26]。例如,新材料為何能提高電池性能;電池中鋰枝晶形成,電解質(zhì)分子分解和SEI膜形成的機(jī)理;催化過程中催化反應(yīng)機(jī)理等。針對(duì)這些問題,需要從材料電子結(jié)構(gòu)的角度出發(fā)去尋求突破,而傳統(tǒng)的經(jīng)典熱力學(xué)無法處理這樣復(fù)雜的問題。因此,量子力學(xué)的密度泛函理論(QDFT)作為一種重要的方法,可用來描述并定量計(jì)算該熱力學(xué)問題。
QDFT 求解體系的電子結(jié)構(gòu)和能量信息最初的思想是通過Schr?dinger方程求解體系的波函數(shù)來獲得[27-28],如式(1)。
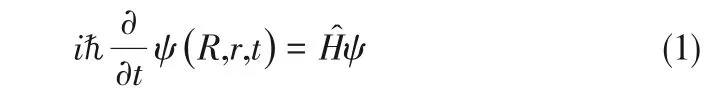
但是實(shí)際體系非常復(fù)雜,要嚴(yán)格求出Schr?dinger方程是不可能的,所以必須在物理模型上作一系列的近似和假定才能求得多電子體系中的電子結(jié)構(gòu)。因此,Born 和Oppenheimer 等[29-30]提出原子核質(zhì)量比電子的質(zhì)量大得多,電子運(yùn)動(dòng)的速度遠(yuǎn)遠(yuǎn)大于原子核運(yùn)動(dòng)的速度,因此可以把原子核認(rèn)為是近似不動(dòng)的點(diǎn)電荷,可以根據(jù)Born-Oppenheimer 近似把體系的波函數(shù)分離成電子波函數(shù)和核波函數(shù)的乘積。隨后,經(jīng)過Hartree、Fock和Slater[31]對(duì)方程進(jìn)行改進(jìn)提出了Hartree-Fock 方程,如式(2)。
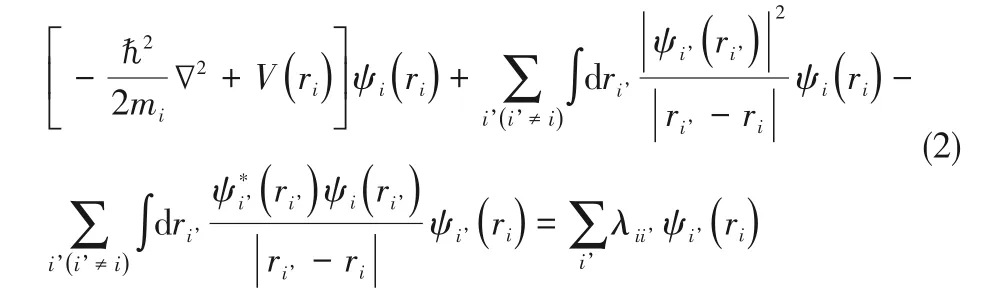
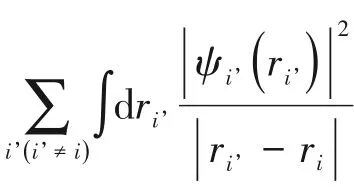
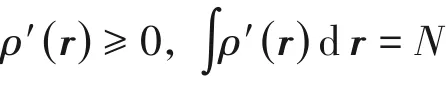
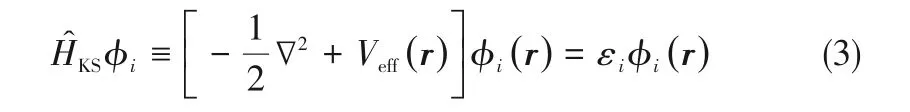
其中

在求解Kohn-Sham 方程時(shí)候必須知道泛函和交換相關(guān)項(xiàng)即第三項(xiàng)的關(guān)系,交換相關(guān)項(xiàng)分為交換能和相關(guān)能。目前來說,沒有得到交換相關(guān)項(xiàng)的準(zhǔn)確函數(shù)表達(dá)形式,但是得到了非常實(shí)用的近似泛函形式,其中主要有局域密度近似(LDA)泛函[34]、廣義梯度近似(GGA)泛函[35-37]。
QDFT 以Hohenberg-Kohn 定 理 以 及Kohn 和Sham 所提出的方程為基礎(chǔ),經(jīng)過幾十年的發(fā)展,在物理、化學(xué)和材料等領(lǐng)域被廣泛的應(yīng)用。通過QDFT 方法,電化學(xué)中吸附能和擴(kuò)散活化能的計(jì)算、鋰枝晶形成的機(jī)理等問題都可以迎刃而解。
在儲(chǔ)能材料領(lǐng)域,主要問題體現(xiàn)在對(duì)吸附能和擴(kuò)散活化能的計(jì)算上。眾所周知,作為一個(gè)良好的儲(chǔ)能材料需要對(duì)帶電離子(鋰離子、鈉離子等)具有良好的吸附性能,并且也要有利于這些帶電離子在材料上的擴(kuò)散。良好的吸附和擴(kuò)散性能體現(xiàn)在能量上就是需要大的吸附能和低的擴(kuò)散活化能。Tang等[38]利用QDFT 計(jì)算了鋰離子在Ti3C2以及Ti3C2X2(X=F、OH)上的吸附能和擴(kuò)散活化能,如圖1 所示。結(jié)果表明,在Ti3C2上有官能團(tuán)修飾時(shí),是不利于離子的擴(kuò)散的。Tang 等通過計(jì)算認(rèn)為,Ti3C2是鋰離子電池中良好的儲(chǔ)能材料,但是當(dāng)表面有官能團(tuán)(—F 或者—OH)修飾時(shí),電池的儲(chǔ)鋰性能將會(huì)下降。因此,實(shí)驗(yàn)中應(yīng)該避免Ti3C2表面—F、—OH 等官能團(tuán)的修飾。Zhou 等[39]通過QDFT 計(jì)算了Li2S6在不同金屬硫化物材料(Ni3S2、SnS2、FeS、CoS2、VS2、TiS2)上的吸附能以及鋰離子在這些材料上的擴(kuò)散活化能,結(jié)果如圖2所示。他們的結(jié)果顯示Li2S6在VS2、TiS2和CoS2上的吸附能較大,并且鋰離子在這些材料上的擴(kuò)散活化能較小。因此,他們預(yù)測(cè)VS2、TiS2和CoS2作為電極材料可以提高鋰硫電池的性能,并且通過實(shí)驗(yàn)證實(shí)了他們的觀點(diǎn)。
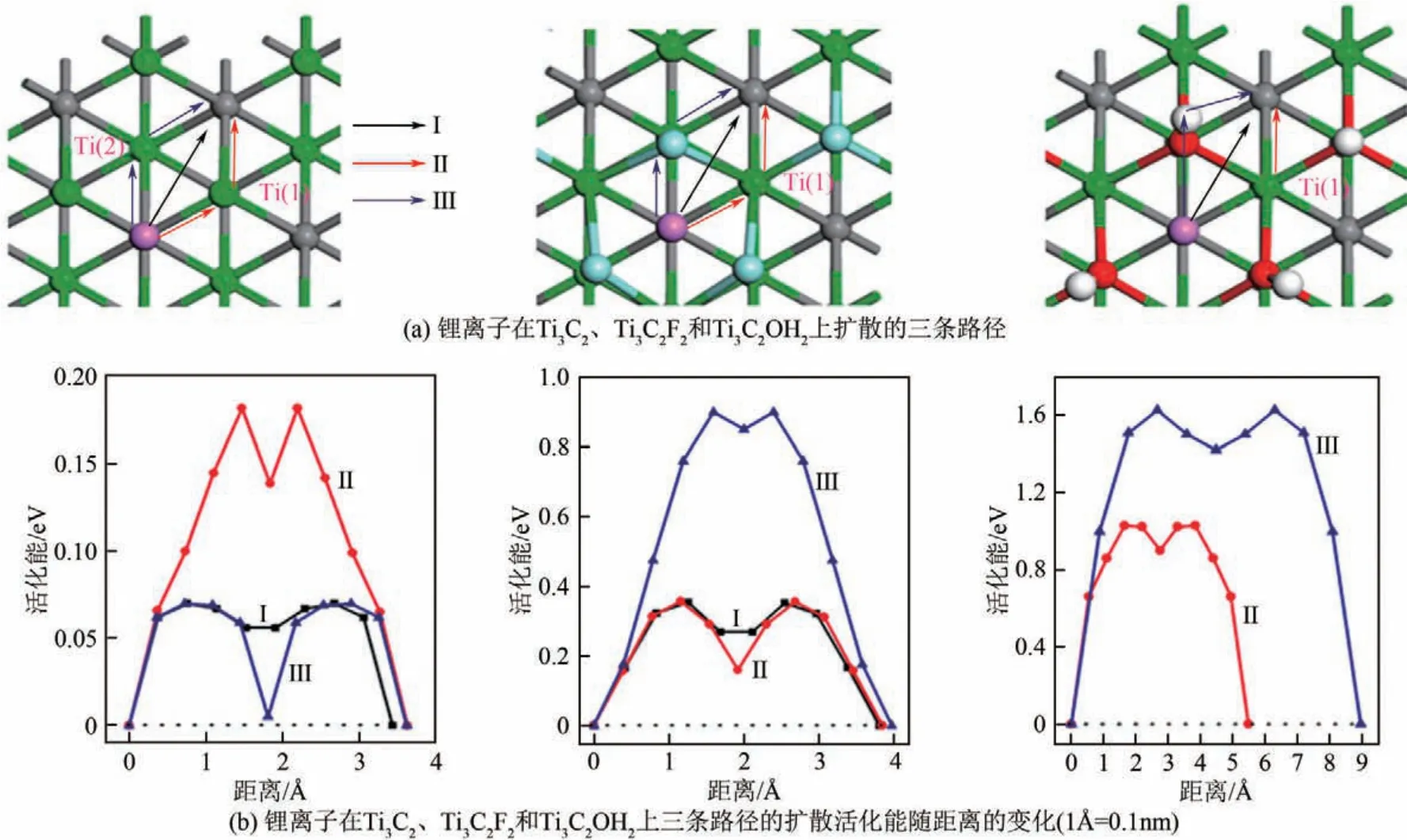
圖1 鋰離子在Ti3C2、Ti3C2F2和Ti3C2OH2上擴(kuò)散的三條路徑和對(duì)應(yīng)的擴(kuò)散活化能[38]
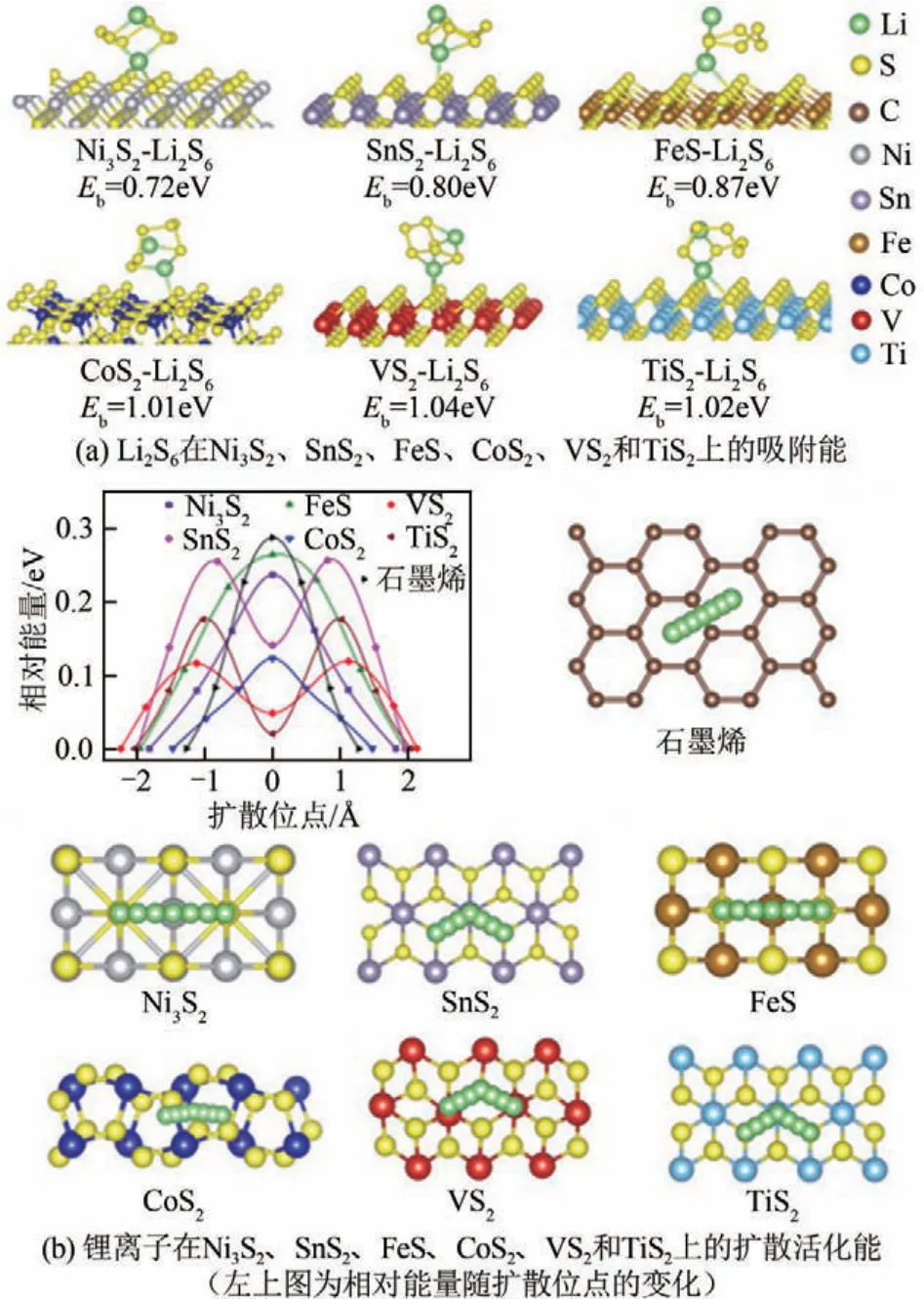
圖2 Li2S6在多種材料上的吸附能與鋰離子在多種材料上的擴(kuò)散活化能[39]
QDFT 還可以研究鋰枝晶形成的機(jī)理。本文作者課題組先前的研究[40]通過QDFT 證明成核是鋰晶體在理想界面上生長(zhǎng)的關(guān)鍵。位錯(cuò)缺陷降低了第一個(gè)鋰原子的吸附能,并對(duì)鋰晶體的生長(zhǎng)產(chǎn)生了長(zhǎng)期的影響。對(duì)于雜原子缺陷,如圖3所示,Cl原子漂浮在鋰晶體上,可以抑制鋰枝晶的生長(zhǎng)。

圖3 使用QDFT進(jìn)行幾何優(yōu)化前后Cl原子的位置發(fā)生變化[40]
QDFT 除了得到能量方面的信息外,還可以得到例如態(tài)密度(DOS)、電荷密度、差分電荷密度和軌道等電子結(jié)構(gòu)方面的信息。這些信息對(duì)儲(chǔ)能材料的篩選也有很大的幫助[38,41-43]。
2.2.2 經(jīng)典密度泛函理論(CDFT)
電化學(xué)相關(guān)材料表界面平衡及非平衡態(tài)性質(zhì)是一個(gè)重要的熱力學(xué)課題,探究粒子在帶電表面(孔道)、受限空間中的分布對(duì)于電化學(xué)系統(tǒng)的設(shè)計(jì)有重要意義。為了精確描述并定量計(jì)算,在傳統(tǒng)半經(jīng)驗(yàn)分子熱力學(xué)統(tǒng)計(jì)方法的基礎(chǔ)上,發(fā)展出了經(jīng)典密度泛函理論(CDFT),其可保留宏觀系統(tǒng)的微觀體系;而相比分子動(dòng)力學(xué)模擬,具有更高的計(jì)算效率。
經(jīng)典密度泛函理論是基于Hohenberg-Kohn 定理[32]建立的,定理指出,在體積、溫度和流體化學(xué)勢(shì)(μ)一定的開放體系,即巨正則系綜中,每種分子的潛在化學(xué)外勢(shì)ψi(r),只由體系平衡時(shí)的密度分布ρi(r)所決定。對(duì)于單組分體系,內(nèi)在Helmholtz自由能可表示為式(5)。
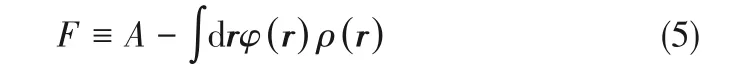
其中,A為Helmholtz 自由能。內(nèi)在Helmholtz自由能與巨勢(shì)能的關(guān)系可表示為式(6)。

內(nèi)在Helmholtz 自由能以及巨勢(shì)能是粒子/分子的單體密度分布的函數(shù),當(dāng)巨勢(shì)能取極小值時(shí),可獲得系統(tǒng)平衡態(tài)的微觀結(jié)構(gòu)和宏觀熱力學(xué)性質(zhì),如式(7)。

拓展到多組分流體,巨勢(shì)能和流體的內(nèi)在Helmholtz自由能可通過勒讓德(Legendre)變換互相關(guān)聯(lián),如式(8)。
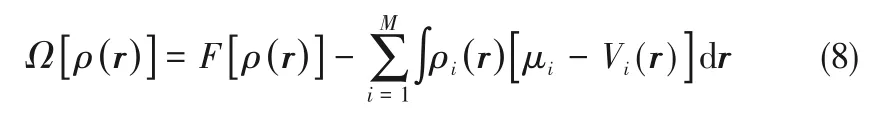
ρ(r)=[ρ1(r),ρ2(r),???,ρM(r)],其中ρi(r)、μi和Vi(r)分別為第i種粒子的密度分布、化學(xué)勢(shì)和外勢(shì)的作用能。
系統(tǒng)的內(nèi)在Helmholtz 自由能可分為兩部分:理想氣體Helmholtz 自由能Fid以及來自分子間相互作用力的過剩項(xiàng)Fex,如式(9)。
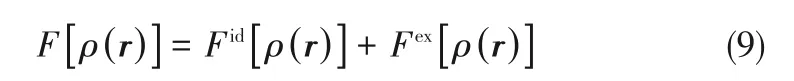
對(duì)于多組分流體,理想氣體Helmholtz 自由能通過統(tǒng)計(jì)力學(xué)推導(dǎo),可表示為式(10)。

進(jìn)一步可得到非均勻流體理想氣體的內(nèi)在Helmholtz自由能,如式(11)。

精確表示過剩Helmholtz自由能對(duì)于CDFT計(jì)算至關(guān)重要,然而確切公式通常是未知的。因此只能采用各種近似,以描述流體分子間復(fù)雜的相互作用。
若能得到剩余自由能對(duì)密度分布的泛函表達(dá)式,將式(8)~式(11)代入式(7)可得描述流體密度分布的Euler-Lagrange方程。
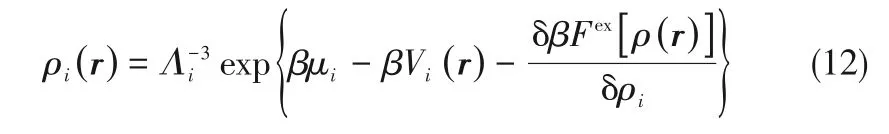
目前主要有兩種方法用于計(jì)算體系的過剩Helmholtz 自由能:一是泛函密度展開;二是將過剩Helmholtz自由能分解[44-46]。
得益于CDFT的準(zhǔn)確性和高效率,它已成為研究超級(jí)電容器電極中雙電層結(jié)構(gòu)和電化學(xué)性能的理想工具。Jiang 和Wu 等[47-48]利用CDFT 預(yù)測(cè)了帶電平板表面的離子液體分布情況。如圖4所示,帶電平板表面吸附反離子(與平板帶電性相反),形成帶電量相反的緊密層,進(jìn)而形成共電極材料離子層(與平板帶電性相同)。同理,依次形成陰陽離子層交錯(cuò)的結(jié)構(gòu),這也與實(shí)驗(yàn)及其他模擬方法如MD[49-50]、MFT[51]、MC[52-53]的預(yù)測(cè)結(jié)果保持一致。
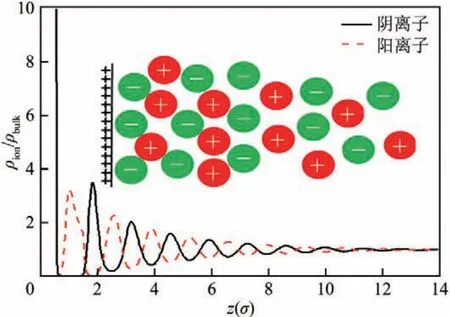
圖4 離子液體電解液在帶電平板表面的分布(ρion/ρbulk)隨位置(z)的變化
求解電極材料表面附近雙電層的結(jié)構(gòu)后,根據(jù)下列公式可計(jì)算不同外電勢(shì)下電極材料中儲(chǔ)存的電荷總量Q、微分電容CD和積分電容C,如式(13)。
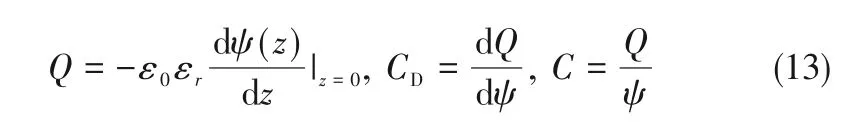
在此基礎(chǔ)上,通過研究表界面性質(zhì),還可以探究電極材料[54-58]與電解液[59-61]對(duì)于超級(jí)電容器性能的影響。
2.2.3 聯(lián)合密度泛函理論(JDFT)
為了進(jìn)一步提高電容器等儲(chǔ)能設(shè)備的電化學(xué)性能,多種新型電極及電解質(zhì)材料已被廣泛應(yīng)用。此時(shí),固液界面環(huán)境十分復(fù)雜:當(dāng)電極界面不能假設(shè)為理想的金屬或硬壁邊界時(shí),電極化學(xué)將起到十分重要的作用。直接利用量子密度泛函理論處理整個(gè)體系,計(jì)算成本高,現(xiàn)階段難以實(shí)現(xiàn)。因此,Arias等[62]提出聯(lián)合密度泛函理論(JDFT),以自洽高效地解決固液表界面問題。
JDFT 利用QDFT 處理溶質(zhì),同時(shí)利用CDFT 處理溶劑。通過最小化總的自由能,可得到平衡狀態(tài)下的固液界面性質(zhì)。JDFT 中自由能可表達(dá)為式(14)。

式中,AHK是Hohenberg-Kohn Theorems 提出的電子能;Alq是經(jīng)典密度泛函表示的液體自由能[63];ΔA是源于溶質(zhì)與溶劑相互作用的耦合能量。
對(duì)于雙電極系統(tǒng),工作電極的電勢(shì)μ定義為單個(gè)電子從工作電極(電化學(xué)勢(shì)μW)遷移到參比電極(電化學(xué)勢(shì)μR)的能量,即ε = μR- μW。如果選定參比電極的電勢(shì)為0,即ε =-μ。當(dāng)電極在模擬中為電中性時(shí),μ 和零電荷電勢(shì)(PZC)有關(guān)。通過對(duì)比理論預(yù)測(cè)和實(shí)驗(yàn)標(biāo)準(zhǔn)的PZC,可得到標(biāo)準(zhǔn)氫電極的電勢(shì)。隨后即可作出不同表面電荷下電極電勢(shì)曲線,通過微分計(jì)算可得到電極電容。
以超級(jí)電容器中廣泛應(yīng)用的石墨烯材料為例,與傳統(tǒng)碳電極不同,電容來自于雙電層電容以及量子電容兩部分的貢獻(xiàn)。前者來自帶電界面的電子-溶劑排斥作用,將影響雙電層的結(jié)構(gòu)和屏蔽電位。后者來自額外的電極電勢(shì)降,當(dāng)電極帶電時(shí),電子開始占據(jù)較高能態(tài),因此降低了整體電容。通過將經(jīng)典模擬中的雙電層電容與電子結(jié)構(gòu)中的法拉第電容相結(jié)合,可以計(jì)算整體電容,如式(15)。

對(duì)于2D 材料,量子電容和雙電層電容相當(dāng),量子電容對(duì)總電容的影響不可忽略。Zhan等[64]利用JDFT 研究了石墨烯層數(shù)對(duì)量子電容及總電容的影響。JDFT 還可用來考察石墨烯超級(jí)電容器的介電屏蔽[65]、邊緣效應(yīng)[66]甚至是贗電容器的充放電機(jī)制(如RuO2[67]、MXene[68]),由此獲得更加真實(shí)的電極材料性質(zhì)及其與電化學(xué)性能間的構(gòu)效關(guān)系。
JDFT 也被證明是金屬電池材料表界面性質(zhì)研究的良好工具,在原子層面上理解電極電解質(zhì)界面的物理過程對(duì)于設(shè)計(jì)改性電池十分重要。金屬材料如鋰、鈉具有高能量密度的特點(diǎn),已被廣泛應(yīng)用為電池陽極材料。然而它們?cè)诔潆姇r(shí)會(huì)局部成核,并形成針狀結(jié)構(gòu),阻礙了其商業(yè)化發(fā)展與應(yīng)用。Gunceler等[69]利用JDFT預(yù)測(cè)電解質(zhì)中鹵化物陰離子(特別是氟離子)的存在會(huì)使得Li+在鋰電極電解質(zhì)界面擴(kuò)散的活化能壘降低0.13eV。這可將表面擴(kuò)散率增加兩個(gè)數(shù)量級(jí)以上,大幅改善鋰電沉積的穩(wěn)定性并抑制液體電解質(zhì)中枝晶的生長(zhǎng),隨后的實(shí)驗(yàn)也驗(yàn)證了這一猜想[70-71]。Ozhabes等[72]更深入地在原子水平上探索了鹵化物陰離子抑制枝晶的機(jī)制。
由于JDFT 準(zhǔn)確高效地解決了固液界面問題,已在儲(chǔ)能設(shè)備、燃料電池領(lǐng)域的機(jī)制探究上取得重大突破。隨著相關(guān)理論基礎(chǔ)的進(jìn)一步完善,JDFT有希望指導(dǎo)更多電化學(xué)相關(guān)材料的設(shè)計(jì)優(yōu)化。
2.2.4 分子動(dòng)力學(xué)(MD)
能量的儲(chǔ)存、釋放和轉(zhuǎn)化往往伴隨著微觀行為(如擴(kuò)散、吸附、化學(xué)反應(yīng)等)的發(fā)生,想要更深入地認(rèn)識(shí)這些過程,就需要使用分子模擬從原子尺度上進(jìn)行更加細(xì)致的研究。利用QDFT等量子化學(xué)計(jì)算手段,可以在原子、電子層面研究體系中的各種微觀性質(zhì);利用CDFT、DDFT等半經(jīng)驗(yàn)的統(tǒng)計(jì)熱力學(xué)方法,可以將微觀性質(zhì)與介觀、宏觀的現(xiàn)象進(jìn)行結(jié)合。前者具有很高的可靠性和精確性,但無法直接對(duì)動(dòng)態(tài)過程中的現(xiàn)象進(jìn)行描述;后者雖然能夠預(yù)測(cè)介觀、宏觀上的現(xiàn)象,但無法表現(xiàn)粒子的具體行為。
為解決上述問題,分子動(dòng)力學(xué)(MD)應(yīng)運(yùn)而生。發(fā)展最成熟、應(yīng)用最廣泛的分子動(dòng)力學(xué)方法是力場(chǎng)分子動(dòng)力學(xué)(FFMD),但其無法描述化學(xué)反應(yīng),對(duì)未知或復(fù)雜的體系也難以作出可靠的模擬,因此發(fā)展出了兩種更為先進(jìn)的分子動(dòng)力學(xué)方法:基于反應(yīng)力場(chǎng)的分子動(dòng)力學(xué)(ReaxFF MD)以及從頭算分子動(dòng)力學(xué)(AIMD)。
(1)力場(chǎng)分子動(dòng)力學(xué)(FFMD) 分子動(dòng)力學(xué)方法是Alder 和Wainwright[73]在1957 年開創(chuàng)的,他們提出了基于剛球勢(shì)的分子動(dòng)力學(xué)方法。Rahman[74]于1964 年利用Lennard-Jones 勢(shì)函數(shù)對(duì)液態(tài)氬的性質(zhì)進(jìn)行了模擬,Rahman 和Stillinger 在1971 年模擬了具有分子團(tuán)簇行為的水的性質(zhì),1977 年Rychaert 和Ciccotti 等提出了約束動(dòng)力學(xué)方法。此后,人們對(duì)這種方法作了很多方面的改進(jìn),尤其是1980 年后,隨著計(jì)算機(jī)技術(shù)的快速發(fā)展以及多體勢(shì)函數(shù)的提出和發(fā)展,更加加速了分子動(dòng)力學(xué)模擬技術(shù)的發(fā)展運(yùn)用。
具體來說,分子動(dòng)力學(xué)模擬是以分子(原子或其他離子,為方便描述故統(tǒng)稱為分子)作為基本的研究對(duì)象,把待模擬系統(tǒng)看作大量分子的集合,運(yùn)用經(jīng)典力學(xué)或者量子力學(xué)的方法來研究這些分子的運(yùn)動(dòng)規(guī)律,從而最終得到體系的宏觀性質(zhì)和基本規(guī)律。分子動(dòng)力學(xué)首先要選取合適的力場(chǎng)。力場(chǎng)是勢(shì)能函數(shù)的經(jīng)驗(yàn)表達(dá)式。分子的勢(shì)能是各類型勢(shì)能的總和,包括非鍵結(jié)勢(shì)能、鍵伸縮勢(shì)能、鍵角彎曲勢(shì)能、二面角扭曲勢(shì)能、離平面振動(dòng)勢(shì)能和庫侖靜電勢(shì)能。自分子動(dòng)力學(xué)模擬方法開創(chuàng)以來,計(jì)算所使用的力場(chǎng)也一直在發(fā)展,研究者針對(duì)不同應(yīng)用目的發(fā)展出各種不同的力場(chǎng),所以不同的力場(chǎng)各有其優(yōu)點(diǎn)和適用范圍,這也就決定了在應(yīng)用分子動(dòng)力學(xué)模擬時(shí)要根據(jù)模擬的系統(tǒng)選擇最合適的力場(chǎng)。
在電解過程中,由于電極表面吸附的水的參與,廣泛用作電解質(zhì)的濕潤(rùn)疏水性離子液體的電化學(xué)窗口減小了。Chen等[75]使用FFMD探討在濕潤(rùn)離子液體中添加鋰鹽對(duì)電極表面吸附水的影響,結(jié)果表明,通過加鹽,大部分水分子被從陰極和陽極排斥開。該工作提供了潛在的機(jī)制和一個(gè)簡(jiǎn)單但實(shí)用的方法來保護(hù)潮濕的離子液體免受電化學(xué)性能退化。
有機(jī)溶劑/水混合電解質(zhì)是一種很有發(fā)展前途的新一代儲(chǔ)能裝置,是工業(yè)電氣化和脫碳的關(guān)鍵。然而,人們對(duì)納米多孔超級(jí)電容器電極中電解質(zhì)離子的擴(kuò)散行為知之甚少。Li等[76]通過實(shí)驗(yàn)和數(shù)值模擬對(duì)超級(jí)電容器的電阻和離子動(dòng)力學(xué)進(jìn)行了系統(tǒng)的研究。在納米多孔電極上的電化學(xué)結(jié)果顯示,超級(jí)電容器電阻隨溶劑遷移率的增加呈非單調(diào)(先減小,后增大,再減小)的趨勢(shì),這對(duì)長(zhǎng)期以來認(rèn)為超級(jí)電容器電阻隨有機(jī)溶劑遷移率的增加而減小的觀點(diǎn)提出了挑戰(zhàn)。通過對(duì)0.95nm納米通道內(nèi)電解質(zhì)離子擴(kuò)散的分子動(dòng)力學(xué)數(shù)值模擬,驗(yàn)證了這種反常趨勢(shì)。以上進(jìn)一步證實(shí)了溶劑分子的范德華尺寸和孔道寬度在確定納米多孔電極電解質(zhì)電導(dǎo)率中的關(guān)鍵相互作用。
Ma等[77]應(yīng)用FFMD來描述具有多孔碳電極的咪唑離子液體,建立了包括狹縫和圓柱孔在內(nèi)的基本幾何模型,以確定離子在充放電過程中的行為。通過研究局部電荷的變化,表明電極的電荷或極化與離子動(dòng)力學(xué)或弛豫有關(guān),特別是在電極附近。探索了實(shí)現(xiàn)循環(huán)伏安法和電化學(xué)阻抗譜技術(shù)的途徑。
氧化石墨烯(GO)納米通道中的離子液體(IL)流動(dòng)對(duì)基于IL 和GO 的流體裝置和其他化學(xué)分離技術(shù)的性能起著關(guān)鍵作用。Wang 等[78]通過分子動(dòng)力學(xué)模擬研究了離子液體在GO納米通道中的流動(dòng)行為,確定了滑移速度與剪切應(yīng)力之間的定量關(guān)系,證實(shí)了GO附近IL層結(jié)構(gòu)的變化是界面性質(zhì)發(fā)生巨大變化的原因。此外,由于受限離子液體庫侖有序的部分破壞,黏度會(huì)隨著羥基化程度的增加而增加。同時(shí),由于IL/GO界面具有較強(qiáng)的相互作用網(wǎng)絡(luò),羥基對(duì)IL流動(dòng)的影響比水在GO納米通道中的影響更為顯著。發(fā)現(xiàn)羥基化是一種令人信服的方法來調(diào)節(jié)IL在納米通道中的流動(dòng)。
(2)基于反應(yīng)力場(chǎng)的分子動(dòng)力學(xué)(ReaxFF MD) 大規(guī)模ReaxFF-MD 模擬得到的原子軌跡和鍵級(jí)信息中蘊(yùn)含著復(fù)雜的化學(xué)反應(yīng)信息,便于進(jìn)行人工分析機(jī)理。基于反應(yīng)力場(chǎng)的分子動(dòng)力學(xué)模擬(ReaxFF MD)在化學(xué)物理學(xué)、材料科學(xué)以及生物物理學(xué)發(fā)揮著舉足輕重的作用。ReaxFF 反應(yīng)力場(chǎng)的方法已經(jīng)成功地應(yīng)用于一些反應(yīng)動(dòng)力學(xué)模擬的研究中,應(yīng)用體系包括碳?xì)溆袡C(jī)小分子體系、高分子體系、高能材料體系、金屬氧化物體系以及過渡金屬催化劑體系[79-80]。
ReaxFF 反應(yīng)力場(chǎng)是van Duin 及其同事開發(fā)的[81]。反應(yīng)分子動(dòng)力學(xué)(ReaxFF MD)是一種極具潛力可應(yīng)用于模擬較大規(guī)模分子體系(>10000個(gè)原子)的化學(xué)反應(yīng)的新方法。
ReaxFF系統(tǒng)能量描述如式(16)。

式中,各項(xiàng)分別為孤對(duì)電子能量修正項(xiàng)Elp;過配位能量校正項(xiàng)Eover、Eunder;價(jià)角能量項(xiàng)Eval;鍵角能量懲罰項(xiàng)Epen;四體共軛項(xiàng)Econj、Etors;三體共軛項(xiàng)Ecoa;C2修正項(xiàng)EC2;范德華作用項(xiàng)EvdWaals;庫侖作用項(xiàng)ECoulomb;氫鍵作用項(xiàng)EH-bond。
研究者利用ReaxFF MD 方法可以探究鋰離子在電解液中的存在形態(tài)與擴(kuò)散情況、SEI膜的形成機(jī)理與結(jié)構(gòu)、鋰離子在電極之間的傳輸方式等。Hossain 等[82]將ReaxFF 反應(yīng)力場(chǎng)參數(shù)集擴(kuò)展到有機(jī)電解質(zhì)種類,例如碳酸亞乙烯酯、碳酸亞乙酯、LiPF6鹽以及碳酸乙基甲基酯;并利用該力場(chǎng)研究了鋰離子和鋰原子分別對(duì)于鋰溶劑化的反應(yīng)機(jī)制。該工作對(duì)初始充、放電循環(huán)期間電解質(zhì)分解的機(jī)理進(jìn)行了闡釋。
對(duì)于鋰離子電池陽極,電極材料的高鋰容量,穩(wěn)定的循環(huán)性能一直是人們研究的熱點(diǎn)。
從圖5(a)中可以看出,硅的理論容量高達(dá)4200mAh/g。因此,硅-氧-碳雜化納米結(jié)構(gòu)作為鋰離子電池的有希望的負(fù)極材料受到了廣泛關(guān)注。
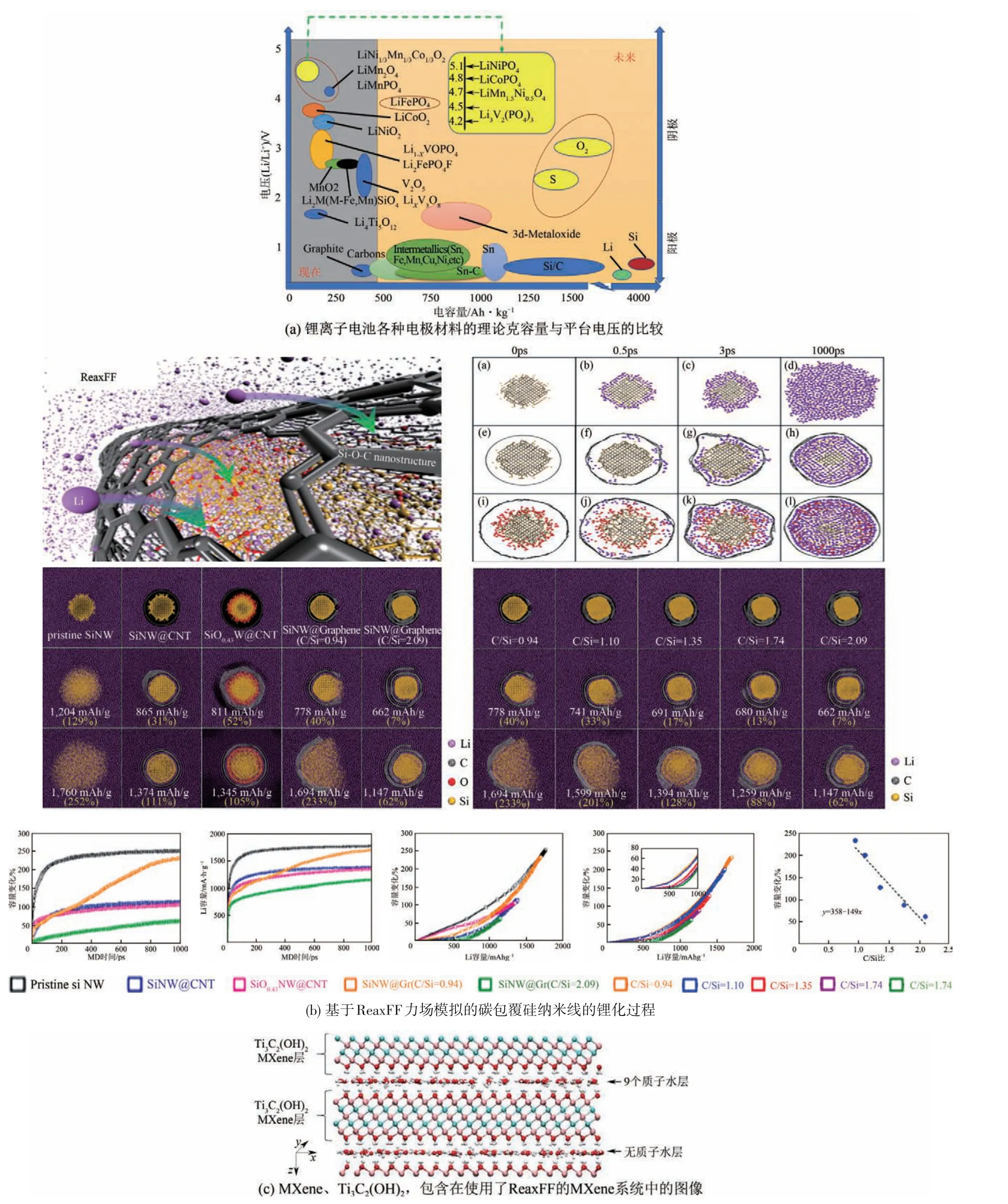
圖5 基于反應(yīng)力場(chǎng)的分子動(dòng)力學(xué)示意圖[83-85]
Han 等[83-84]在Si/C/O/Li 反應(yīng)力場(chǎng)開發(fā)方面做出許多重要工作。報(bào)告了不同種類的硅陽極(原始硅和SiOx),各種碳酸鹽電解質(zhì)的不同類型和組成以及添加劑對(duì)SEI形成的影響。隨后,該團(tuán)隊(duì)利用該力場(chǎng)研究了sp2 碳包覆的Si 和SiOx納米結(jié)構(gòu)(例如納米線(NWs)和納米顆粒(NPs))的原子鋰化行為。該工作為Si-O-C 混合陽極的設(shè)計(jì)提供了理論指導(dǎo)意義。具體工作如圖5(b)所示。
MXenes 最近發(fā)現(xiàn)的二維(2D)材料,由于其出色的電導(dǎo)率,可作為超級(jí)電容器電極材料,這引起了研究者極大的興趣[85]。通過ReaxFF-MD 分析了位于9個(gè)不同溫度(200K、250K、260K、270K、280K、290K、300K、350K、400K) 下 的 雙 層MXene層之間的單層水中的質(zhì)子遷移,對(duì)三個(gè)獨(dú)立創(chuàng)建的MXene-水模型的仿真中,發(fā)現(xiàn)質(zhì)子擴(kuò)散常數(shù)隨溫度升高而變化的異常趨勢(shì)。如圖5(c)所示。
(3)從頭算分子動(dòng)力學(xué)(AIMD) 經(jīng)過數(shù)十年的發(fā)展,人們已經(jīng)針對(duì)多種原子、分子(或基團(tuán))、粗粒化粒子和不同體系建立了分子力場(chǎng),但遠(yuǎn)未能完全滿足分子動(dòng)力學(xué)研究的需要,對(duì)于復(fù)雜、未知的體系往往難以獲得可靠的結(jié)果。此外,力場(chǎng)分子動(dòng)力學(xué)的模擬結(jié)果完全取決于力場(chǎng)參數(shù),而這些參數(shù)來自于實(shí)驗(yàn)測(cè)定和量化計(jì)算的結(jié)果,只能體現(xiàn)原子、分子層面的特征信息,如果行為受電子層面的性質(zhì)變化影響很大,力場(chǎng)分子動(dòng)力學(xué)將難以描述。
從頭算分子動(dòng)力學(xué)(AIMD)是一種使用量子化學(xué)方法計(jì)算原子的受力情況,可以從電子層面出發(fā)描述粒子的動(dòng)態(tài)行為,其計(jì)算基本流程如圖6所示。因其基于量化計(jì)算,具有精度高、可靠性好、普適性強(qiáng)的優(yōu)點(diǎn),并且可以對(duì)化學(xué)反應(yīng)的本征過程進(jìn)行表現(xiàn)。但是,AIMD 的計(jì)算成本更加昂貴,在相同體系下的時(shí)間成本相對(duì)于FFMD 高出幾個(gè)數(shù)量級(jí)[86]。

圖6 AIMD模擬的基本流程
在納米尺度的約束下,流體中的粒子表現(xiàn)出與在體積(Bulk)區(qū)完全不同的行為。利用AIMD,能夠以高的準(zhǔn)確性和可靠性對(duì)粒子的反常擴(kuò)散和傳輸進(jìn)行動(dòng)態(tài)研究[87-91]。
Mo 等[89]率先在鋰離子導(dǎo)體材料的離子擴(kuò)散研究中應(yīng)用AIMD 模擬,自此以后AIMD 作為一種研究快速離子導(dǎo)體的標(biāo)準(zhǔn)技術(shù)被用于Na+、Mg2+、O2-等很多種離子的研究中[92-94]。AIMD(以及經(jīng)典MD)的優(yōu)勢(shì)在于,材料中的擴(kuò)散行為直接從原子的動(dòng)力學(xué)軌跡中觀測(cè),而不是人為指定了擴(kuò)散機(jī)制。對(duì)于復(fù)雜材料(如超離子導(dǎo)體)而言,其擴(kuò)散機(jī)制的猜測(cè)十分困難,且無法保證猜測(cè)的可靠性,AIMD 模擬在發(fā)現(xiàn)和識(shí)別不同體系的遷移機(jī)制方面發(fā)揮了獨(dú)特作用,如最近對(duì)超離子導(dǎo)體的研究發(fā)現(xiàn),鋰石榴石[91,95]等中的遷移行為是多離子協(xié)同的結(jié)果,而非孤立離子的跳躍。此外,AIMD 模擬可以對(duì)擴(kuò)散行為影響因素的貢獻(xiàn)進(jìn)行采樣和統(tǒng)計(jì),這對(duì)建立該體系中擴(kuò)散機(jī)制的數(shù)學(xué)模型有極大的幫助。
目前,AIMD 模擬已經(jīng)成為研究擴(kuò)散機(jī)制和特定材料的擴(kuò)散特性時(shí)廣泛使用的手段。使用AIMD模擬來提取擴(kuò)散特性需要解決三個(gè)問題:①以最小誤差從模擬結(jié)果中提取擴(kuò)散特性;②將提取出的擴(kuò)散特性的誤差進(jìn)行量化;③可靠的物理范圍。為此,He等[96]建立了分析程序,從AIMD模擬結(jié)果中提取擴(kuò)散特性并量化其統(tǒng)計(jì)誤差,并估計(jì)了AIMD模擬可用的溫度范圍。
3 電化學(xué)的非平衡態(tài)熱力學(xué)
3.1 非平衡態(tài)熱力學(xué)概述
目前,以平衡態(tài)和可逆過程為基礎(chǔ)的平衡態(tài)熱力學(xué)已經(jīng)形成了完善的理論結(jié)構(gòu)并廣泛的用于各種物理、化學(xué)過程的研究。然而,平衡態(tài)熱力學(xué)僅研究平衡態(tài)及其過程的特殊情況,有很大的局限性[97-99]。熱力學(xué)在非平衡態(tài)過程中的應(yīng)用有多種形式,最簡(jiǎn)單的是基于局部平衡假設(shè)的線性非平衡態(tài)熱力學(xué)。假定非平衡態(tài)過程發(fā)生的系統(tǒng)可以被分成一系列小區(qū)域,每一個(gè)小區(qū)域的熱力學(xué)性質(zhì)都和平衡態(tài)一致。局部平衡假設(shè)是否使用于某一系統(tǒng)取決于是否存在兩個(gè)大小不同的弛豫時(shí)間,即是否存在遠(yuǎn)小于整個(gè)體系達(dá)到統(tǒng)計(jì)平衡的弛豫時(shí)間τ的時(shí)間τr,使在時(shí)間間隔τr內(nèi),這些小區(qū)域可以建立局部平衡。局部平衡概念適用于各種常見的氣體和液體的宏觀系統(tǒng),以及大多數(shù)反應(yīng)過程的碰撞速率小于總碰撞速率的運(yùn)輸過程和化學(xué)反應(yīng),而不適用于在碰撞非常稀少的高度稀有氣體。另一種眾所周知的應(yīng)用是第二定律分析法,這一分析方法基于Gouy-Sodola定理,說明由于過程的不可逆性,損失的可用能與熵增成正比。熵增的程度被用作與判斷過程最優(yōu)性的標(biāo)準(zhǔn),主要通過減少過程的不可逆性去減少有用功的耗散和自然資源的枯竭。
3.2 非平衡態(tài)熱力學(xué)在電化學(xué)能源存儲(chǔ)與轉(zhuǎn)換領(lǐng)域的應(yīng)用
在電化學(xué)相關(guān)材料的制備和應(yīng)用領(lǐng)域,其包含的過程更復(fù)雜,如擴(kuò)散、遷移、傳熱、流體流動(dòng)、化學(xué)反應(yīng),甚至耗散結(jié)構(gòu)主導(dǎo)的過程[100]。這些不可逆過程在儲(chǔ)能和轉(zhuǎn)換系統(tǒng)中是高度耦合的,并且隨著時(shí)間的推移,從非平衡態(tài)到平衡態(tài)發(fā)展。根據(jù)線性非平衡熱力學(xué),可以用響應(yīng)矩陣的非對(duì)角項(xiàng)來描述不同熱力學(xué)力對(duì)電化學(xué)系統(tǒng)中離子輸運(yùn)的耦合效應(yīng)。解析法側(cè)重于通過數(shù)學(xué)推導(dǎo)求解唯象系數(shù)矩陣,矩陣的非對(duì)角項(xiàng)描述不同熱力學(xué)力的相互作用。分子建模已被廣泛應(yīng)用于研究一些特殊的輸運(yùn)現(xiàn)象,如充電動(dòng)力學(xué)、電動(dòng)現(xiàn)象和熱電效應(yīng),這些現(xiàn)象可以提供關(guān)于輸運(yùn)過程的詳細(xì)信息,但需要大量的計(jì)算工作。連續(xù)性模擬是快速探索電化學(xué)系統(tǒng)動(dòng)態(tài)特性的一種有效方法,但它受到稀釋溶液理論的限制,使該理論不適用于分子尺度或高外加電位下。而動(dòng)態(tài)密度泛函理論(DDFT)可以在考慮空間效應(yīng)和其他相互作用的情況下,快速和準(zhǔn)確地研究這些運(yùn)輸過程。
如圖7 所示,DDFT 是一種綜合方法,忽略過量化學(xué)勢(shì)就得到Nernst-Planck (NP)方程。將DDFT與包括泊松方程、Navier-Stokes(NS)方程、熱方程和Butler-Volmer(BV)方程在內(nèi)的其他幾個(gè)偏微分方程耦合起來可用于描述電化學(xué)相關(guān)材料制備及應(yīng)用過程中的多種非平衡態(tài)過程。

圖7 電解質(zhì)非平衡熱力學(xué)的動(dòng)態(tài)DFT理論
Poisson-Nernst-Planck (PNP) 方 程[101-102]既 描述了溶液中物質(zhì)的質(zhì)量傳遞,又描述了電解質(zhì)中的電勢(shì)分布,可用于研究與其他過程方程耦合的非平衡過程,如NS方程、熱方程和BV方程。
本節(jié)基于非平衡態(tài)熱力學(xué),從傳質(zhì)、反應(yīng)和傳遞耦合、熱效應(yīng)三個(gè)角度來理解電化學(xué)能量?jī)?chǔ)存與轉(zhuǎn)換過程。
3.2.1 非平衡態(tài)傳質(zhì)
實(shí)際化工過程大多為非平衡態(tài)過程,而其中最重要的粒子行為就是傳質(zhì)。不受外力作用時(shí),電解質(zhì)中的離子會(huì)永不停息地做隨機(jī)運(yùn)動(dòng),而在外電場(chǎng)的作用下,沿著帶電表面流動(dòng)的電解質(zhì)不僅可以由壓力梯度驅(qū)動(dòng),也可以由電壓差產(chǎn)生的電場(chǎng)驅(qū)動(dòng),形成傳質(zhì)現(xiàn)象,也叫離子遷移。非平衡態(tài)熱力學(xué)在經(jīng)典熱力學(xué)、分子和統(tǒng)計(jì)熱力學(xué)的基礎(chǔ)上,考慮了時(shí)間t的影響,也就是粒子隨時(shí)間的變化過程。
在某一系統(tǒng)中,假設(shè)含有i種與電極接觸的離子,zi為對(duì)應(yīng)的化合價(jià),ε為介電常數(shù),n為黏度,T為溫度。連續(xù)性方程如式(17)。
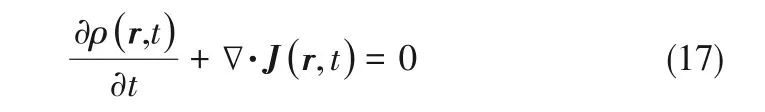
對(duì)于通量,這里考慮擴(kuò)散和遷移的貢獻(xiàn),首先考慮擴(kuò)散的貢獻(xiàn),由通用的菲克定律給出,如式(18)。

式中,J是“流”;化學(xué)勢(shì)μ的梯度是熱力學(xué)“力”,是粒子密度分布,而Γ=D/kBT是遷移率。化學(xué)勢(shì)μ可以分為本征項(xiàng)μint和外場(chǎng)項(xiàng)μext,其中本征項(xiàng)μint的推導(dǎo)與CDFT 類似,取決于系統(tǒng)的Helmholtz 自由能,如式(19)。

其中,F(xiàn)[ρ]= Fid[ρ(r)]+ Fexc[ρ(r)],包括理想自由能Fid和剩余自由能Fexc,理想自由能可以表示為式(20)。
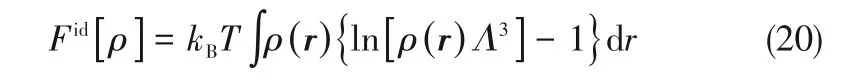
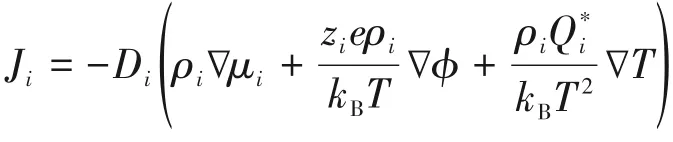
在穩(wěn)態(tài)假設(shè)下,通量與從高濃度區(qū)域到低濃度區(qū)域的梯度成正比,如式(21)。

其中,Di是擴(kuò)散系數(shù)或擴(kuò)散系數(shù)。其次,考慮遷移的貢獻(xiàn),利用愛因斯坦關(guān)系,可以用波動(dòng)耗散引起的擴(kuò)散系數(shù)來表示,如式(22)。

其中,vi指通量速度;E 指系統(tǒng)內(nèi)的電場(chǎng)。速度是電力(ZieE)與Stokesian 摩擦項(xiàng)(6πηαi,αi是離子半徑)之間的比值。
綜上,可得到通量的表現(xiàn)形式如式(23)。
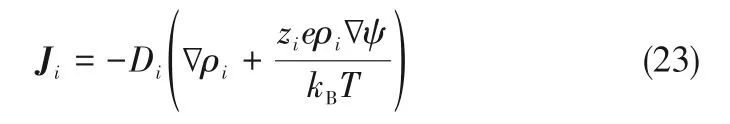
這一關(guān)系常用于電化學(xué)與電化學(xué)分析領(lǐng)域。
在電化學(xué)能源存儲(chǔ)領(lǐng)域,超級(jí)電容器可以提供比電池更高的輸出功率,并且可以提供比介電電容器更多的能量[104]。由于碳電極包含大量的納米孔并可被流動(dòng)性離子液體填充,許多類型的碳基材料已用于電容器電極的制造中。然而,實(shí)驗(yàn)測(cè)量的超級(jí)電容器充電和放電時(shí)間尺度與現(xiàn)有的理論預(yù)測(cè)之間存在很大的差距,并且多孔結(jié)構(gòu)與宏觀超級(jí)電容器的充電點(diǎn)和動(dòng)力學(xué)之間的關(guān)系仍然不清楚。Lian等[103]提出了一個(gè)用于解釋超級(jí)電容器充電動(dòng)力學(xué)的新模型,如圖8(a)所示,將電極結(jié)構(gòu)近似為一系列無限薄的平行板堆疊而成,平行板的間隙即典型孔的寬度。模型成功減少了理論預(yù)測(cè)與實(shí)驗(yàn)測(cè)量結(jié)果之間的時(shí)間尺度差距,并可作為擴(kuò)展突破平面對(duì)稱性的基礎(chǔ)。
鋰離子電池作為一種傳統(tǒng)的二次電池,依靠鋰離子在正負(fù)極之間的移動(dòng)來轉(zhuǎn)換能量,為實(shí)現(xiàn)更高的安全性與能量密度,全固態(tài)鋰離子電池有望成為新一代鋰離子電池。全固態(tài)鋰離子電池的核心組成部分就是固體無極快離子導(dǎo)體。He 等[91]基于密度泛函理論的分子動(dòng)力學(xué)模擬了如圖8(b)所示的擴(kuò)散模型。
在圖中所示的擴(kuò)散模型中,四個(gè)流動(dòng)離子排列在一個(gè)由兩個(gè)單元組成的一維晶格中。整個(gè)移動(dòng)晶格的總能量E 由晶體骨架(即能量景觀)的勢(shì)能φ 和移動(dòng)離子之間的庫侖相互作用給出,如式(24)。
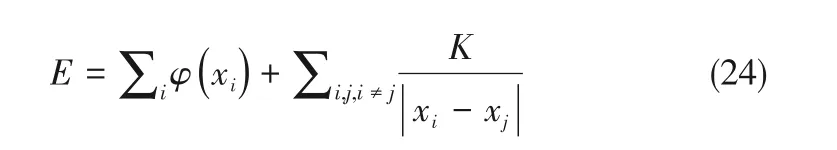
其中,xi是離子i的位置;K是兩個(gè)流動(dòng)離子之間的庫侖相互作用強(qiáng)度。
該模型闡明了協(xié)同離子擴(kuò)散的低能勢(shì)壘是超離子導(dǎo)體中獨(dú)特的移動(dòng)離子構(gòu)型和強(qiáng)的移動(dòng)離子相互作用的結(jié)果,為設(shè)計(jì)具有快速離子擴(kuò)散的固體材料提供了一般的框架和通用的策略。
半導(dǎo)體光催化技術(shù)[圖8(c)]能夠把豐富的太陽能轉(zhuǎn)化為化學(xué)能,是維持地球的未來發(fā)展的潛在技術(shù)。在半導(dǎo)體光催化過程中,半導(dǎo)體體相內(nèi)電子和空穴的復(fù)合過程比電荷傳輸和電荷表面催化過程快,這導(dǎo)致半導(dǎo)體光催化劑的體相電荷分離效率降低,嚴(yán)重阻礙了半導(dǎo)體光催化技術(shù)的發(fā)展與實(shí)際應(yīng)用。Li等[105]發(fā)展了一種通過內(nèi)電場(chǎng)調(diào)控來提高半導(dǎo)體光催化劑體相電荷分離效率的全新策略,獲得了較高的體相電荷分離效率。

圖8 超級(jí)電容器及其電極堆疊模型、鋰離子電池?cái)U(kuò)散模型、半導(dǎo)體光催化劑示意圖[91,103]
3.2.2 反應(yīng)和傳遞的耦合
在非平衡態(tài)熱力學(xué)解決了傳質(zhì)問題后,反應(yīng)和傳遞耦合問題也普遍體現(xiàn)在電化學(xué)的儲(chǔ)存和轉(zhuǎn)化過程中,以備受關(guān)注的電催化反應(yīng)為例,其可持續(xù)發(fā)展的模式是以太陽能、風(fēng)能和水力能等可再生的電化學(xué)作為動(dòng)力,通過電化學(xué)過程將水、二氧化碳和氮?dú)獾刃》肿愚D(zhuǎn)化成高附加值的產(chǎn)品,如氫氣、烴類、氧化物和胺,其中涉及析氫反應(yīng)(HER)、氧還原反應(yīng)(ORR)、二氧化碳還原反應(yīng)(CO2RR)以及氮還原反應(yīng)(NRR)。對(duì)于電催化的發(fā)展,為了指導(dǎo)高性能電催化劑材料的開發(fā)和制備,一個(gè)很重要的前沿是利用實(shí)驗(yàn)和計(jì)算方法快速分析和解釋在大量不同類別的催化劑上以及在不同的操作條件(如pH、溶劑和電解質(zhì)等)下的反應(yīng)過程和機(jī)制[106]。為了研究在催化劑和電解液界面發(fā)生的各種傳遞和反應(yīng)耦合過程,動(dòng)態(tài)密度泛函理論(DDFT)是一個(gè)有效的手段,它是CDFT 在動(dòng)力學(xué)上的延伸,以化學(xué)勢(shì)梯度驅(qū)動(dòng)密度分布[100]。通過很多不同的推導(dǎo)過程都可以得到標(biāo)準(zhǔn)的DDFT 形式,基于唯象理論和線性非平衡態(tài)熱力學(xué)理論的推導(dǎo)方法是其中最快的,它的出發(fā)點(diǎn)是通用菲克定律,見式(18)。
由式(17)~式(20)可以獲得DDFT 方程的標(biāo)準(zhǔn)形式,如式(25)。

對(duì)于化學(xué)勢(shì)μ(r,t),如果只考慮本征項(xiàng)中的理想自由能以及外場(chǎng)項(xiàng)中的外加平均電勢(shì),進(jìn)一步耦合Poisson 方程,可以得到上述的PNP 方程,而表面電極反應(yīng)可以用BV方程表示,如式(26)。

式中,i0是交換電流密度;αa和αc是量綱為1的陽極和陰極電荷轉(zhuǎn)移系數(shù);n是所涉及的電子數(shù);F是法拉第常數(shù);R是氣體常數(shù)。這樣,可以利用得到的PNP-BV方程去解決電催化體系中的傳遞和反應(yīng)的耦合問題,比如通過計(jì)算電極尖端的電場(chǎng)、離子分布和電流密度來描述電極尖端曲率對(duì)電催化二氧化碳還原的影響[圖9(a)][107]。對(duì)于電化學(xué)系統(tǒng),理解離子在微結(jié)構(gòu)電極中的傳輸過程對(duì)多孔電極的設(shè)計(jì)十分重要,Suter 和Haussener[108]利用實(shí)驗(yàn)上的電極幾何結(jié)構(gòu)構(gòu)建了一個(gè)三維的傳質(zhì)模型[圖9(b)],并考慮電解質(zhì)溶液中的KCO3緩沖反應(yīng),以及通過上述的BV 方程表示電極表面的催化反應(yīng),來計(jì)算CO2還原成CO的過程中局部的濃度分布,進(jìn)而從優(yōu)化電極幾何和傳質(zhì)的角度提升CO的選擇性。
在上述PNP 方程推導(dǎo)的基礎(chǔ)上,如果再考慮本征項(xiàng)μint中剩余自由能Fexc的體積排斥項(xiàng)Fhs[ρ],就可以得到修正的通量表達(dá)式,如式(27)。
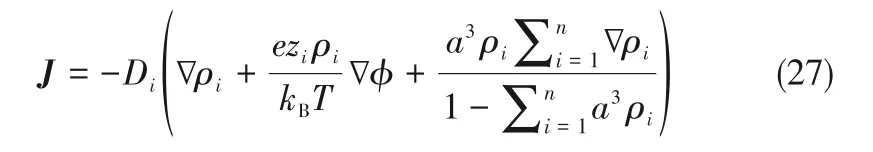
式中,?是電勢(shì);a是分子或離子的尺寸。再進(jìn)一步結(jié)合式(17)和Poisson 方程,就得到了修正的PNP 方程。Bohra 等[109]利用通用修正的PNP 方程(GMPNP)描述了電催化CO2還原體系中電極附近的擴(kuò)散、遷移和反應(yīng)耦合的現(xiàn)象[圖9(c)],其中考慮了因?yàn)槿苜|(zhì)分子或離子的溶劑化尺寸所引起的體積排阻效應(yīng),比較準(zhǔn)確地計(jì)算了雙電層區(qū)域的電勢(shì)和濃度分布,以及雙電層結(jié)構(gòu)對(duì)CO2擴(kuò)散的影響。研究傳遞和反應(yīng)耦合現(xiàn)象時(shí),外場(chǎng)除了電勢(shì)外,流體流動(dòng)的影響也十分重要,Lis 等[110]首次從實(shí)驗(yàn)上報(bào)道了流體流動(dòng)對(duì)界面反應(yīng)與EDL 結(jié)構(gòu)的影響,將微流體與表面特性SFG光譜學(xué)相結(jié)合證明流體流動(dòng)導(dǎo)致界面水分子的可逆重新排列和浸沒表面的表面電荷變化。同樣,動(dòng)態(tài)密度泛函理論也可以用于研究流體流動(dòng)對(duì)界面反應(yīng)的影響,Lian等[111]將經(jīng)典密度泛函理論與NS 方程以及反應(yīng)動(dòng)力學(xué)結(jié)合來研究溶劑流動(dòng)與表面化學(xué)反應(yīng)的關(guān)系[圖9(d)],發(fā)現(xiàn)固體表面的溶劑流動(dòng)對(duì)表面反應(yīng)有顯著的影響,進(jìn)而影響表面電荷密度,因此在高的驅(qū)動(dòng)壓力下,流動(dòng)電流隨壓力呈現(xiàn)出非線性的關(guān)系。
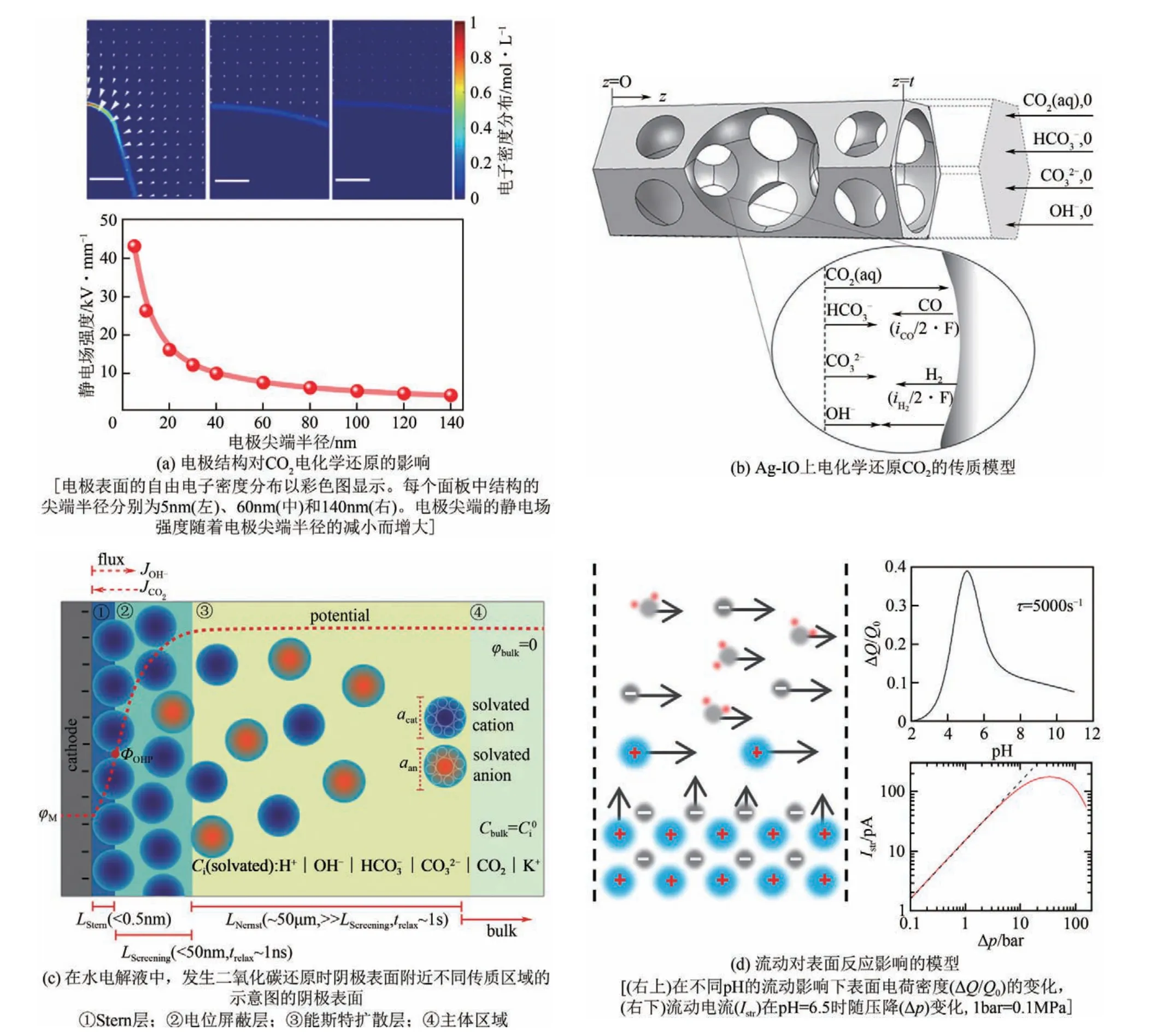
圖9 反應(yīng)和傳遞的耦合示意圖[107-109,111]
3.2.3 熱效應(yīng)
在非平衡態(tài)熱力學(xué)關(guān)注的領(lǐng)域,除了主要的傳質(zhì)與反應(yīng)問題外,熱效應(yīng)也是與幾乎所有電化學(xué)過程息息相關(guān)的,且這個(gè)過程是非平衡的,因此前文所述經(jīng)典化工熱力學(xué)、分子和統(tǒng)計(jì)熱力學(xué)都無能為力,而非平衡態(tài)熱力學(xué)則可以在一定程度上解決這個(gè)問題。熱效應(yīng)主要分為兩個(gè)方面,即電生熱、熱生電。
(1)電生熱 高溫會(huì)導(dǎo)致材料老化、內(nèi)阻增大、電容降低、發(fā)生電化學(xué)副反應(yīng)和自放電等問題。而低溫會(huì)使化學(xué)反應(yīng)速度變慢,電解液阻值變大,鋰離子穿越性能變差,活性降低,放電的電流變小,電池的可用容量降低。通過建模可以更好地理解能量轉(zhuǎn)換裝置的熱行為。
PNP方程假設(shè)物理系統(tǒng)是等溫的,并使用恒定的溫度來描述,這可能適用于那些溫度變化很小的系統(tǒng)。然而,電流通常伴隨著焦耳熱效應(yīng),導(dǎo)致相當(dāng)大的溫度變化。d'Entremont 等[112]提出了一種新的雙電層電容恒流充放電過程中離子耦合傳熱的物理模型[圖10(a)]。該模型利用修正的PNP模型解釋了Stern 層的存在和離子的有限大小。模擬結(jié)果定性地再現(xiàn)了文獻(xiàn)報(bào)道的各種充放電條件下的實(shí)驗(yàn)數(shù)據(jù)[圖10(b)]。Hsieh 等[113]利用能量變分方法導(dǎo)出了一個(gè)非等溫電動(dòng)力學(xué)模型。用變溫度下的PNP 方程描述電荷輸運(yùn),熱流滿足傅里葉定律。這種Poisson-Nernst-Planck-Fourier模型既滿足熱力學(xué)第一定律和第二定律,又滿足Onsager 的倒數(shù)關(guān)系,因此它是熱力學(xué)一致的。最后,利用能量法證明了該模型在初始數(shù)據(jù)很小的假設(shè)下的全局適定性。
目前對(duì)于雙電層形成過程中發(fā)生的可逆熱效應(yīng)仍然缺乏統(tǒng)一的認(rèn)識(shí),充電的熱響應(yīng)也沒有得到充分的研究。從熱力學(xué)的觀點(diǎn)來看,在充電過程中,超級(jí)電容器的電極熵的表面電荷被反離子電荷屏蔽,因此離子構(gòu)型熵降低。對(duì)于一個(gè)準(zhǔn)靜態(tài)帶電的絕熱超級(jí)電容器,熱力學(xué)要求其滿足等熵的條件。離子減少的構(gòu)型熵被增加的電解質(zhì)熵(升溫)所抵消[圖10(c)]。從動(dòng)力學(xué)觀點(diǎn)來看,在放電過程中,反離子必須越來越多地?cái)U(kuò)散回溶液中。這種擴(kuò)散是在對(duì)抗電力時(shí)發(fā)生的。提高這些離子的電能所需的能量必須從周圍的離子和分子中吸收,并從后者的熱運(yùn)動(dòng)中以動(dòng)能的形式傳遞。因此,絕熱的超級(jí)電容器在放電時(shí)降溫。Jamssen 等[114]對(duì)超級(jí)電容器可逆加熱的不同觀點(diǎn)進(jìn)行了詳細(xì)的比較,在定量上調(diào)和了可逆加熱的兩種觀點(diǎn),討論了熱力學(xué)觀點(diǎn)中的等熵過程的理想氣體等熵壓縮模型(含亥姆霍茲和古伊-查普曼吸附)和應(yīng)用麥克斯韋關(guān)系式和巨勢(shì)函數(shù)的模型,其中只有后者的結(jié)果與動(dòng)力學(xué)的觀點(diǎn)中的PNP方程耦合熱方程相一致[圖10(d)]。
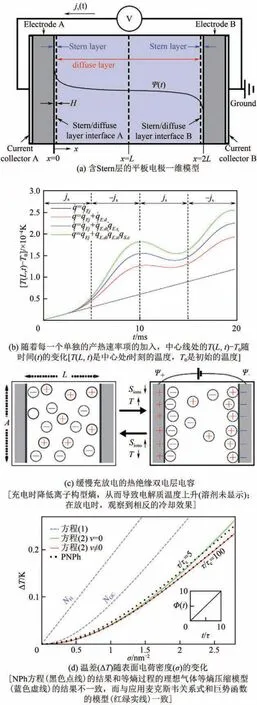
圖10 熱效應(yīng)電生熱示意圖[112,114]
(2)熱生電 低品質(zhì)的熱(低于373K)普遍存在于實(shí)際生產(chǎn)中,包括來自工業(yè)廢熱流、太陽能加熱、地?zé)崴畮臁⒑Q鬅崽荻取⑸镔|(zhì)發(fā)酵甚至數(shù)據(jù)中心的廢熱,是主要的可持續(xù)能源。但由于目前的回收技術(shù)不具成本效益,因此大部分都被浪費(fèi)了。熱電效應(yīng)表示溫度梯度和電壓梯度之間存在直接轉(zhuǎn)換。通過熱電效應(yīng),可以直接將低品質(zhì)的熱能轉(zhuǎn)換為電能。
溫度演化與電流的耦合對(duì)理解電解液系統(tǒng)的動(dòng)力學(xué)特性具有重要意義,近年來引起了廣泛的關(guān)注。Janssen等[115]利用PNP方程耦合熱方程研究了電解槽在其兩個(gè)邊界電極的其中一個(gè)表面突然施加小的溫度升高時(shí)的瞬態(tài)響應(yīng)(圖11)。通過PNP 模型耦合熱方程推導(dǎo)了鹽濃度、電荷量和早期(遠(yuǎn)短于熱弛豫時(shí)間)以及后期(遠(yuǎn)長(zhǎng)于熱弛豫時(shí)間)熱電壓的解析逼近解。對(duì)于陰陽離子擴(kuò)散系數(shù)不相等的電解質(zhì),熱電壓表現(xiàn)出兩步弛豫過程,與實(shí)驗(yàn)數(shù)據(jù)一致[116]。

圖11 熱效應(yīng)熱生電示意圖[115]
雖然已經(jīng)成功揭示了溫度梯度對(duì)離子輸運(yùn)的影響,但目前還沒有詳細(xì)的研究探索納米通道中熱驅(qū)動(dòng)離子輸運(yùn)的調(diào)節(jié)方法,特別是通過溫度差和納米通道長(zhǎng)度來調(diào)節(jié)的方法。Zhong 等[117]建立了基于PNP方程的計(jì)算模型來描述熱驅(qū)動(dòng)離子在納米通道中的輸運(yùn)。研究了不同影響因素對(duì)離子輸運(yùn)的影響,包括納米通道的溫差、離子濃度、納米通道的半寬和納米通道的長(zhǎng)度。結(jié)果表明,離子濃度為1mol/m3、納米通道半寬度為1nm 是理想的用于熱電應(yīng)用的納米通道體系。
與在體相中對(duì)應(yīng)的熱電動(dòng)勢(shì)相比,電解質(zhì)在受限空間里的熱電動(dòng)勢(shì)有很大的不同。電解質(zhì)在體相中的熱電動(dòng)勢(shì)與不同離子的熱泳遷移率有關(guān),而即使每種離子的遷移熱相同或非常小,電解質(zhì)在受限空間里的熱電動(dòng)勢(shì)也可能存在。Dietzel等[118]發(fā)現(xiàn)即使在最簡(jiǎn)單的電解質(zhì)中,如果被限制在帶電的壁之間,也不需要這種Soret 型離子熱擴(kuò)散來誘導(dǎo)熱電效應(yīng)。在約束下的熱電動(dòng)勢(shì)與通道ζ電位或表面電荷密度成正比。雙電層的空間電荷導(dǎo)致了由溫度依賴性的電泳離子遷移率驅(qū)動(dòng)的選擇性離子擴(kuò)散,這對(duì)于狹窄的通道來說,可能會(huì)導(dǎo)致比經(jīng)典Soret 平衡大30 倍的熱電壓。Fu 等[119]采用分子動(dòng)力學(xué)模擬方法研究了被限制在帶電壁之間的氯化鈉和氯化碘溶液的熱電響應(yīng)。結(jié)果表明計(jì)算得到的熱電響應(yīng)比標(biāo)準(zhǔn)圖方法的預(yù)測(cè)大2個(gè)數(shù)量級(jí),這表明納米流體系統(tǒng)的集熱性能可與最佳熱電材料的集熱性能相媲美。這是因?yàn)樗倪^剩焓(在標(biāo)準(zhǔn)圖方法中被忽略)與液固界面的電滲透遷移率結(jié)合起主導(dǎo)作用。因此,使用水動(dòng)力滑移較大的表面可以提高熱電響應(yīng)。
4 用于電化學(xué)相關(guān)材料設(shè)計(jì)的高通量計(jì)算和機(jī)器學(xué)習(xí)
4.1 高通量計(jì)算和機(jī)器學(xué)習(xí)概述
研發(fā)清潔高效且廉價(jià)的電化學(xué)相關(guān)材料對(duì)當(dāng)前世界能源危機(jī)的解決具有重大意義,但一般從產(chǎn)品研發(fā)到投入市場(chǎng)的時(shí)間跨度極大。傳統(tǒng)的發(fā)現(xiàn)新材料的方法,如經(jīng)驗(yàn)試錯(cuò)法和基于密度泛函理論(DFT)的方法[120-122],由于其開發(fā)周期長(zhǎng)、效率低、成本高,已經(jīng)無法跟上當(dāng)今材料科學(xué)的發(fā)展步伐。用于高通量篩選的現(xiàn)代化學(xué)模擬工具包可以幫助人們加速尋找新材料。特別是,通過高通量計(jì)算,無需實(shí)驗(yàn)合成就可以得到材料的一些關(guān)鍵特性[123-124]。而結(jié)合數(shù)據(jù)挖掘技術(shù),以機(jī)器學(xué)習(xí)為核心算法的人工智能技術(shù)由于其計(jì)算成本低、開發(fā)周期短,加上強(qiáng)大的數(shù)據(jù)處理能力和高預(yù)測(cè)性能,正在材料檢測(cè)、材料分析和材料設(shè)計(jì)中廣泛應(yīng)用[125]。
因此,本節(jié)主要討論了高通量計(jì)算和機(jī)器學(xué)習(xí)在電化學(xué)相關(guān)材料的性能預(yù)測(cè)和穩(wěn)定性評(píng)價(jià)、構(gòu)效關(guān)系的建立等方面的成功應(yīng)用。
(1)高通量計(jì)算 高通量計(jì)算通過將組合化學(xué)中的“構(gòu)建單元”和“高通量篩選”觀點(diǎn)用于材料模擬中,通過材料計(jì)算尋找或篩選材料組成的基本構(gòu)建單元,構(gòu)造新的化合物,建立起材料成分、結(jié)構(gòu)、和性能的定量關(guān)系模型來用于指導(dǎo)新材料設(shè)計(jì)。
(2)機(jī)器學(xué)習(xí) 機(jī)器學(xué)習(xí)作為人工智能的一個(gè)分支,在算法的指導(dǎo)下,利用大量的數(shù)據(jù)不斷優(yōu)化模型,作出合理的預(yù)測(cè)。圖12 顯示了一個(gè)完整的機(jī)器學(xué)習(xí)過程,包括數(shù)據(jù)處理、建模和驗(yàn)證[126]。
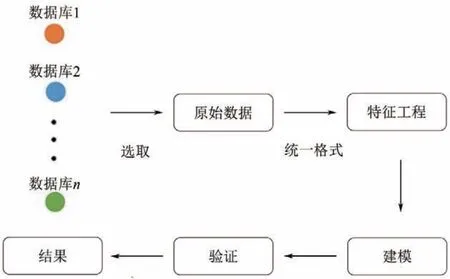
圖12 機(jī)器學(xué)習(xí)的流程(包括數(shù)據(jù)處理、建模和驗(yàn)證)[126]
4.2 材料性能預(yù)測(cè)和穩(wěn)定性評(píng)價(jià)
目前,用于鋰離子電池的電極材料種類繁多,其實(shí)際使用壽命也受到多種因素影響,難以預(yù)測(cè)。因此,如何準(zhǔn)確預(yù)測(cè)鋰離子電池等復(fù)雜非線性系統(tǒng)的壽命對(duì)于加速技術(shù)發(fā)展至關(guān)重要。然而,不同的老化機(jī)制、顯著的設(shè)備變異性和動(dòng)態(tài)的工作條件仍然是主要的挑戰(zhàn)。現(xiàn)有的預(yù)測(cè)鋰離子電池剩余壽命的方法大多依賴于對(duì)老化機(jī)理的先驗(yàn)知識(shí),使用化學(xué)或物理配方和分析電池模型。這種依賴性在實(shí)踐中通常很難確定,這限制了這些方法的應(yīng)用。Severson 等[127]生成了一個(gè)包括124 個(gè)在快速充電條件下循環(huán)的商業(yè)磷酸鐵鋰/石墨電池的數(shù)據(jù)集,其循環(huán)壽命變化很大,從150次到2300次不等。利用早期循環(huán)的放電電壓曲線(尚未顯示容量退化),應(yīng)用機(jī)器學(xué)習(xí)工具根據(jù)循環(huán)壽命預(yù)測(cè)和分類電池。模型在使用前100個(gè)周期(顯示從初始容量中位數(shù)增加0.2%)定量預(yù)測(cè)周期壽命時(shí)達(dá)到9.1%的測(cè)試誤差,使用前5個(gè)周期將周期壽命分為兩組時(shí)達(dá)到4.9%的測(cè)試誤差。Yang 等[128]提出了一種基于統(tǒng)計(jì)知識(shí)的鋰離子電池健康狀態(tài)估計(jì)方法。采用擴(kuò)展卡爾曼濾波-遞歸-最小二乘聯(lián)合算法對(duì)電池充電狀態(tài)進(jìn)行估計(jì),同時(shí)識(shí)別模型參數(shù)和開路電壓。然后采用粒子群優(yōu)化-最小二乘支持向量回歸方法,給出了可靠的健康狀態(tài)估計(jì)結(jié)果,具有較高的精度和良好的泛化能力,粒子群優(yōu)化算法提高了算法的全局尋優(yōu)能力。
超級(jí)電容器作為一種清潔的儲(chǔ)能裝置,具有快速充放電動(dòng)力學(xué)、高功率密度和長(zhǎng)循環(huán)壽命等顯著優(yōu)點(diǎn),已被廣泛應(yīng)用于為汽車電動(dòng)機(jī)提供動(dòng)力。精確評(píng)估超級(jí)電容的剩余使用壽命,為更換損壞電池提供反饋,以維持電動(dòng)汽車的安全性。目前基于數(shù)據(jù)或模型的預(yù)測(cè)的評(píng)估方法要么耗時(shí),要么精度較低。Zhou 等[129]提出了一種基于遞歸神經(jīng)網(wǎng)絡(luò)方法和混合遺傳算法相結(jié)合的通用策略,以實(shí)現(xiàn)對(duì)剩余使用壽命的有效和魯棒性評(píng)估。序列二次規(guī)劃作為遺傳算法的局部搜索算子,增強(qiáng)了遺傳算法的全局搜索能力,以退出概率和隱含層單元數(shù)為手段快速搜索局部最優(yōu)解。最后,將這種預(yù)測(cè)方法應(yīng)用于穩(wěn)態(tài)充電模式下的超級(jí)電容器,成功地估算了其剩余使用壽命。
雖然已經(jīng)有大量關(guān)于溶劑對(duì)超級(jí)電容器性能的影響的實(shí)驗(yàn)和模擬研究,但它們往往耗時(shí)或缺少微觀機(jī)理的認(rèn)識(shí)。因此,需要一種更全面的方法來更好地理解溶劑在超級(jí)電容器上的作用。Su 等[130]采用將機(jī)器學(xué)習(xí)、實(shí)驗(yàn)和分子建模相結(jié)合的方法,研究溶劑對(duì)電容性能的影響,并可用于預(yù)測(cè)和提高超級(jí)電容器的性能。用已發(fā)表的實(shí)驗(yàn)數(shù)據(jù)測(cè)試了5種機(jī)器學(xué)習(xí)模型,包括支持向量回歸、多層感知、M5 模型樹、M5 規(guī)則和線性回歸[圖13(a)],確定了每個(gè)溶劑變量對(duì)電容的相對(duì)重要性。溶劑分子種類和介電常數(shù)是超級(jí)電容器最重要的變量,而溶劑的偶極矩、黏度和沸騰溫度對(duì)其影響不大。Jain等[131]將人工神經(jīng)網(wǎng)絡(luò)技術(shù)應(yīng)用于碳基超級(jí)電容器的電容預(yù)測(cè)。從數(shù)百篇發(fā)表的論文中提取數(shù)據(jù)訓(xùn)練神經(jīng)網(wǎng)絡(luò)模型,選取了比表面積、孔徑、ID/IG比、氮摻雜水平和電壓窗5 個(gè)特征來計(jì)算它們對(duì)電容的影響,然后選取幾個(gè)碳基樣本對(duì)神經(jīng)網(wǎng)絡(luò)的性能進(jìn)行評(píng)價(jià)。結(jié)果表明,與線性回歸、Lasso 回歸等其他機(jī)器學(xué)習(xí)方法相比,人工神經(jīng)網(wǎng)絡(luò)技術(shù)在電容預(yù)測(cè)方面表現(xiàn)出最好的準(zhǔn)確性和適應(yīng)性。
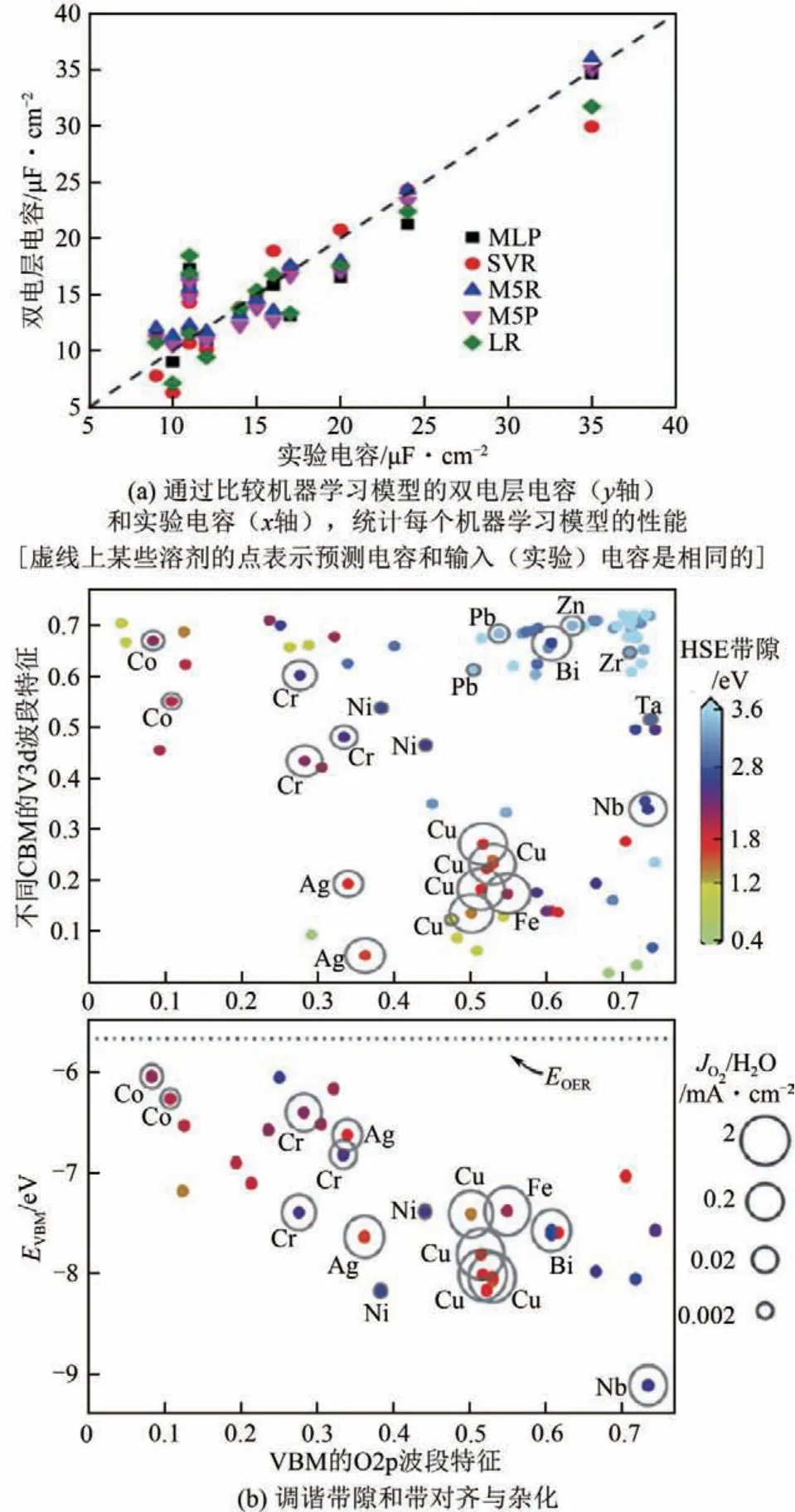
圖13 材料性能預(yù)測(cè)和穩(wěn)定性評(píng)價(jià)示意圖[130,132]
Yan等[132]提出了一種磷酸鹽作為正極材料的高通量從頭算分析方法。容量、電壓、比能量、能量密度和熱穩(wěn)定性的評(píng)估計(jì)算數(shù)以千計(jì)的化合物[圖13(b)]。確定了磷酸鹽化學(xué)固有的重量和容量方面的極限,給出了磷酸鹽中所有氧化還原偶的電壓范圍,分析了影響電壓的結(jié)構(gòu)因素。重新研究磷酸鹽材料是否本質(zhì)上是安全的,并發(fā)現(xiàn)在相同的氧化態(tài)下,磷酸鹽的熱力學(xué)釋氧溫度低于氧化物的。Joshi 等[133]使用深度神經(jīng)網(wǎng)絡(luò)、支持向量機(jī)和核脊回歸,結(jié)合化合物的屬性和其成分的元素屬性的特征向量,來預(yù)測(cè)金屬離子電池電極材料的電壓。首先利用它們生成電壓剖面圖,并將其與密度泛函理論計(jì)算進(jìn)行比較,最后利用該方法提出了近5000 種鈉離子和鉀離子電池的候選電極材料。
4.3 構(gòu)效關(guān)系的建立
隨著高壓可充電電池等儲(chǔ)能系統(tǒng)的發(fā)展,高效地尋找新的電解質(zhì)變得至關(guān)重要。Park等[134]建立了一個(gè)1000000氧化還原勢(shì)組成的搜索地圖,以篩選具有新的核心和官能團(tuán)的有機(jī)添加劑和溶劑,從而建立電解質(zhì)數(shù)據(jù)庫。闡明了氧化還原勢(shì)與官能團(tuán)之間的定量關(guān)系,最后篩選了一種喹諾林化合物作為陽極添加劑,并將其應(yīng)用于電解質(zhì)中,實(shí)驗(yàn)結(jié)果表明,在鋰離子電池循環(huán)近200次時(shí),容量保持率從64.3%提高到80.8%。高電壓和高熱安全性是正極材料的理想特性,但很難同時(shí)實(shí)現(xiàn)。Jain等[135]使用高通量密度泛函理論計(jì)算來評(píng)估超過1400 種正極材料的電壓和安全性(由熱力學(xué)氧氣釋放溫度估計(jì))之間的聯(lián)系。結(jié)果表明電壓與安全性之間存在強(qiáng)烈的反比關(guān)系。并研究了聚陰離子基團(tuán)、氧化還原偶聯(lián)和氧與反陽離子比對(duì)電壓和安全性的影響。總的來說,只有少數(shù)化合物代表有限的氧化還原偶/聚陰離子組合,表現(xiàn)出高電壓和高安全性。
5 結(jié)語
在目前電化學(xué)領(lǐng)域的高速發(fā)展中,化工熱力學(xué)相關(guān)技術(shù)和應(yīng)用對(duì)其發(fā)展具有很大的指導(dǎo)意義。在經(jīng)典熱力學(xué)的基礎(chǔ)上,各種新興的熱力學(xué)領(lǐng)域與研究方法如雨后春筍般蓬勃發(fā)展,對(duì)推動(dòng)電化學(xué)行業(yè)進(jìn)步起到了輔助與加速作用。在經(jīng)典化工熱力學(xué)、分子和統(tǒng)計(jì)熱力學(xué)的堅(jiān)實(shí)基礎(chǔ)上,非平衡態(tài)熱力學(xué)的發(fā)展越來越貼近實(shí)際,可以定量解決大量電化學(xué)過程的模擬計(jì)算問題。高通量計(jì)算和機(jī)器學(xué)習(xí)則是近年來研究人員所使用的新方法,是用于電化學(xué)相關(guān)材料設(shè)計(jì)的利器,也是一個(gè)未來可以大有作為的化工熱力學(xué)分支。如何構(gòu)建完備的非平衡態(tài)熱力學(xué)體系,如何高效利用新興計(jì)算機(jī)技術(shù)來輔助熱力學(xué)的發(fā)展,應(yīng)當(dāng)是今后發(fā)展中應(yīng)重點(diǎn)思考和解決的問題。目前,對(duì)于實(shí)際電化學(xué)問題的解決缺乏連貫性與系統(tǒng)性,更加偏向于逐個(gè)攻破,問題的解決應(yīng)該著力于進(jìn)行多尺度多物理場(chǎng)的耦合計(jì)算,建立起電化學(xué)領(lǐng)域的理論計(jì)算體系,可以從電子尺度、原子尺度、分子尺度、顆粒尺度、器件尺度等多尺度進(jìn)行連貫的計(jì)算,并且耦合電場(chǎng)、速度場(chǎng)、溫度場(chǎng)和反應(yīng)等多物理場(chǎng)的效應(yīng)。在熱力學(xué)的多重研究的加持下,電化學(xué)領(lǐng)域?qū)⒊掷m(xù)高速發(fā)展,在解決人類能源問題中占有越來越重要的地位。

