電網頻率擾動下并網變換器系統暫態穩定性分析

閆 寒，黃 萌，唐英杰，付熙坤，查曉明

（武漢大學電氣與自動化學院，湖北省武漢市 430072）

0 引言

隨著新能源大規模并網，越來越多的電力電子變換器被用作分布式能源與交流電網的接口。與此同時，電力電子裝備也給電網的安全穩定運行帶來影響。與傳統高慣性同步發電機不同，電力電子變換器在電網擾動下具有更為快速和復雜的暫態過程，對并網變換器系統的安全、穩定運行會造成一定的影響。新疆哈密地區發生的風電機組群次/超同步振蕩、河北沽源地區發生的雙饋風電機組群與串聯補償電網相互作用的次同步諧振［1］等表明對并網變換器系統進行暫態穩定性研究是必要的。

在并網過程中，鎖相環（phase-locked loop，PLL）被廣泛用于電壓信號的實時跟蹤，為并網變換器提供頻率以及參考相位。傳統的分析方法采用小信號線性化方法將鎖相環與并網變換器統一建模，例如基于阻抗模型［2］、狀態空間模型［3］的分析方法。鑒于上述2種模型的局限性，基于拉普拉斯（s）變換的節點導納矩陣的網絡諧振結構分析法［4］和幅相模型［5-7］等被進一步提出并用以分析含非同步機電源系統在不同時間尺度下的動態特性。研究結果表明，高鎖相環帶寬［2］以及鎖相環引入的負阻抗［8］都會對系統穩定性造成危害。

在非理想電網條件下，鎖相環由于鑒相作用而存在固有的非線性特性，對并網變流器系統的穩定性造成影響。傳統的鎖相環線性化模型不能完全描述鎖相環的暫態過程，需要對其非線性特性進行分析。文獻［9］分別從非線性動力學以及虛擬同步機的角度揭示了鎖相環的數學和物理本質，并采用李雅普諾夫能量函數分析了鎖相環的穩定條件。文獻［10］將鎖相環近似等效為同步發電機，并用等面積定則（equal-area criterion，EAC）解釋了帶鎖相環的并網變換器失穩機理。然而，EAC的這類應用并不能完全代表鎖相環的控制特性［11-12］。文獻［11］對比了在電網對稱故障下各分析方法的優缺點。文獻［13］通過建立降階非線性模型來解釋鎖相環的不穩定過程和再同步瞬態過程，定性分析了鎖相環控制參數對暫態過程的影響。

當負荷突變或發電機投入、切除時，系統的功率輸入、輸出都會產生不平衡。當系統受到擾動時，功率將重新分配，系統輸入、輸出功率在一定電壓、頻率水平下將呈現不同的暫態特性［14］。文獻［15］指出，當負載增加時，電網頻率下降，同步發電機轉速降低，從而向電網釋放能量。在文獻［11-12］中，對鎖相環二階微分方程的推導是基于電網頻率不變的假設，適用于電網阻抗變化和電流變化的情況。若電網發生頻率擾動時，對鎖相環二階微分方程的推導，則不可避免地要考慮頻率的變化。

本文針對弱電網條件下的頻率擾動工況，推導了鎖相環與電網相角差的暫態輸出方程。基于非線性動力學的多尺度法［16］，定量解析了頻率擾動下鎖相環的二階微分方程，進一步分析了誤差產生的原因。基于解析解，得出暫態穩定判據，為鎖相環的參數設計提供參考。

1 頻率擾動下鎖相環的二階微分方程

本文關注鎖相環受到擾動后的暫態過程，在對電壓環以及電流環進行參數選擇時，按穩定點在工作點附近進行處理。若電流環響應速度足夠快，則可以對其進行解耦，并直接給定電流參考值，因此可設定Id=Idref，Iq=Iqref。其中Id、Iq、Idref、Iqref分別為電流環電流的d軸、q軸分量以及相應的參考值。并網變流器系統的拓撲結構如圖1所示。其中，Ut∠θt、Vg∠θg、E∠θ分別為公共耦合點（point of coupling，PCC）電壓、電網相電壓以及并網逆變器輸出端口電壓；Udc為直流側電壓；θpll為鎖相環輸出相角；ωn為固有角頻率，其值為100π；ω為系統角頻率；t為時間變量；Lf和Cf分別為濾波電感和濾波電容；Ls和Rs分別為電網電感和電網電阻；R和C分別為直流側穩壓電阻和穩壓電容；ia、ib、ic為線路三相電流。

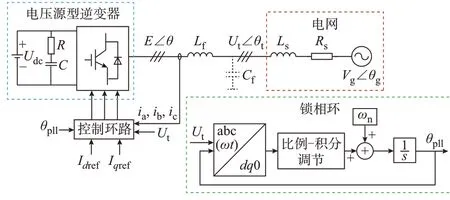
圖1 并網變流器系統結構及鎖相環控制Fig.1 Structure and PLL control of grid-connected converter system

由文獻［15］可知，由輸入、輸出功率不平衡造成的頻率變化率（rate of change of frequency，RoCoF）在一次調頻的最初階段，可以認為以固定斜率k變化。因此，基于鎖相環的時間尺度，本文將頻率擾動設為一次函數。在此基礎上，可以基于文獻［12］推導出在頻率擾動下鎖相環輸出相角的二階微分方程。

在弱電網中，穩定狀態下的PCC處電壓可以表示為：

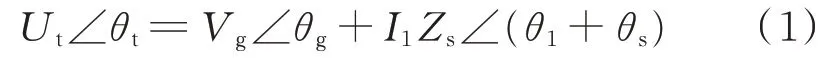
式中：Zs和θs分別為電網阻抗幅值和相角；I1和θ1分別為并網變換器等效電流源的電流幅值和相位。

電流環電流d軸分量設為0，此時θ1=θpll，進一步對式（1）進行dq分解，得到Utq如式（2）所示。

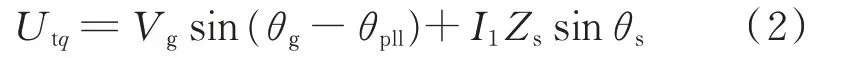
式中：Utq為PCC處電壓幅值的q軸分量。

根據圖1可以得到θpll如式（3）所示。

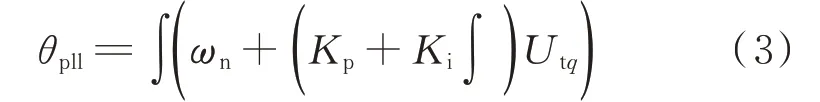
式中：Kp和Ki分別為鎖相環控制器的比例系數和積分系數。

當電網頻率從50 Hz以斜率k線性變化時，電網阻抗與電網角頻率、電感、電阻的關系可進一步表示成式（4）。

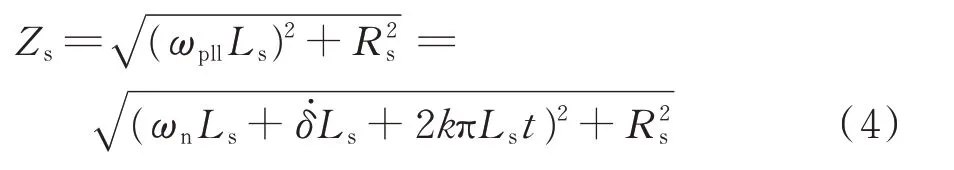
式中：ωpll為鎖相環角速度；δ為相位差。

將式（2）代入式（3），可以進一步推導出考慮頻率擾動時相位差δ的二階微分表達式，如式（5）所示。

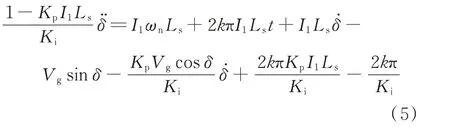
2 基于多尺度法的解析求解方法

電網頻率擾動的存在，使得式（5）存在顯含時間的項，對其解析求解存在困難。由于δ的二階微分方程和非線性動力學的研究對象有相似之處，本文借鑒單自由度非自治系統的多尺度解法，對其進行求解。

2.1 多尺度法的基本原理

文獻［16］指出，多尺度法的基本原理是微擾法，也稱攝動法。它把微分方程的解x（t）視為很多快慢不同時間尺度或變量的函數，從而適用于求取弱非線性系統的瞬態解。

由于微擾法可能會產生長期項，多尺度法可以對這一現象進行改進。多尺度法把微分方程的解不只看作是單一時間自變量t的函數，而是把t，εt，ε2t等看成獨立自變量，利用不同尺度的時間變量，使得漸進解在ε指定階次的范圍內得出一致有效解。

2.2 二階微分方程的解析求解

假設δ受到擾動后存在新的穩態點δ0，為了簡化計算過程以及應用多尺度法，需要對式（5）在新的穩態點處進行泰勒展開。在擾動較小時，可以舍去三次及以上高次項，式（5）可以進一步化簡為：

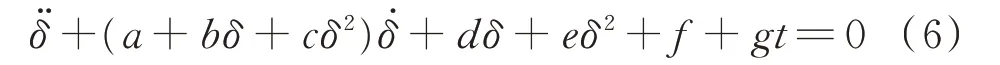
式中：a、b、c、d、e、f、g為相應的泰勒展開系數。

式(6)的推導過程見附錄A式(A1)和式(A2)。由于gt項的存在，在運用多尺度法進行求解的過程中，依舊不可避免地存在長期項，而非線性動力學中的方法更多的是針對外施激勵為周期函數的系統，因此，如果能夠將gt項轉化為周期函數，則能降低解析難度。考慮到鎖相環輸出相角在暫態過程中的時間尺度較小，因此可以在時間的一定范圍內將一次函數處理成正弦函數。附錄A圖A1給出了將一次函數正弦化處理的比較結果。該結果表明，當正弦函數周期越大時，正弦函數與一次函數保持較小誤差的時間跨度越長。因此，式（6）在0≤t≤tmax（tmax是正弦化函數與一次函數保持較小誤差的最大時間）范圍內可以被進一步近似等價為：

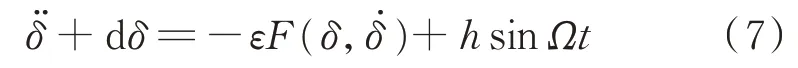
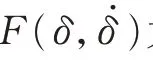
引入變量α、β、γ、λ、η，并令a=εα，b=εβ，c=εγ，e=ελ，f=εη，則有：

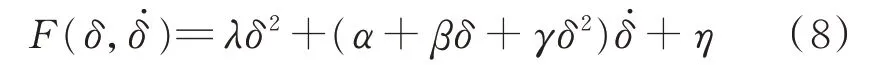
引入2個時間尺度T0和T1，式（7）的一次近似解為：

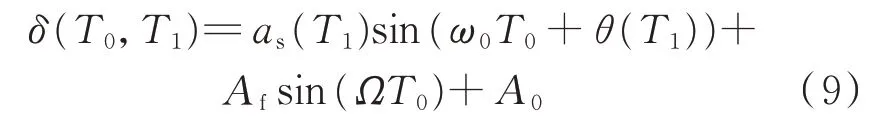
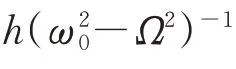
將式（9）代入式（7），并令方程等號兩側ε的同次冪系數相等，進一步消除長期項。當ΩT0盡可能小時，在消 除 長 期 項 過 程 中，cos（ω0T0+θ(T1)±μΩT0）（μ為 正 整 數）項 可 以 與cos（ω0T0+θ(T1)）項 合 并，sin（ω0T0+θ(T1)±μΩT0）項 可 以 與sin（ω0T0+θ(T1)）項合并，可以得到：

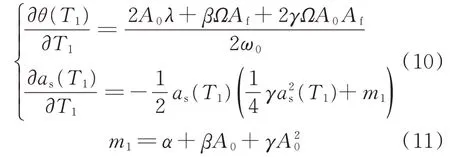
式中：m1為引入的參數。

對式（10）進行積分，可以得到：

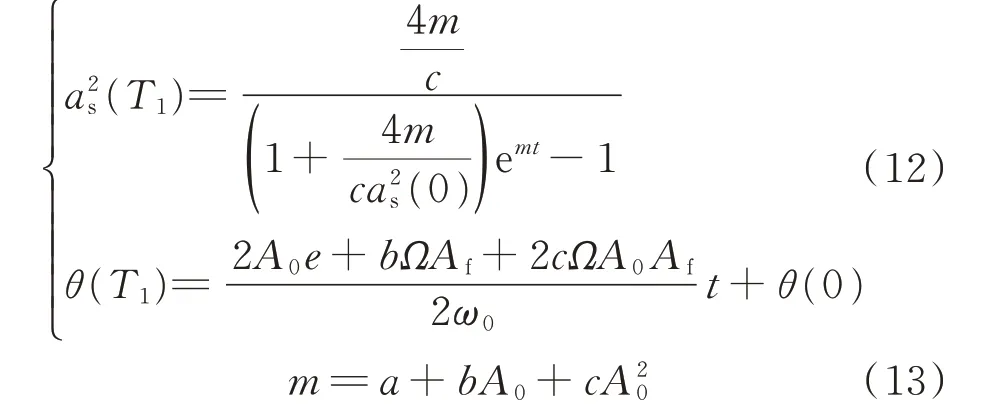
式中：m為引入的參數。

根據實際運行工況，初值可以寫為：

式中：B0為δ在t=0-時刻的初值。

將式（14）代入式（9），可以得到：

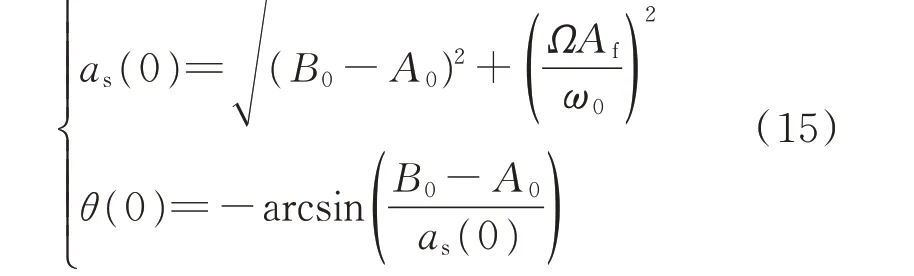
于是得到式（6）的一次近似解：

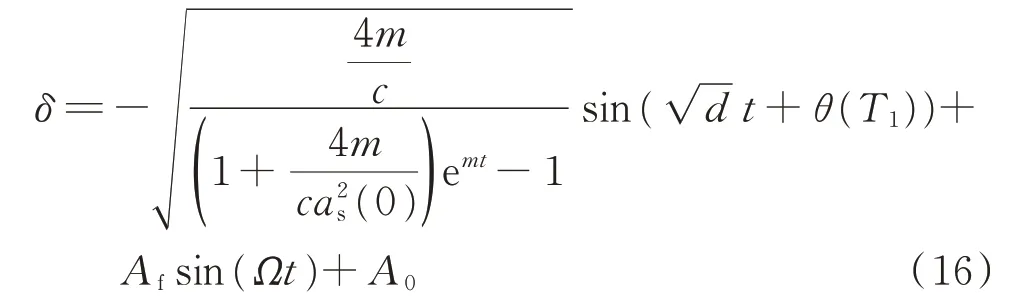
式（16）等號右邊的第1項為自由振動項，第2項為強迫振動項，強迫振動項是由外施激勵引發的。根據式（16），在非共振情況下，若自由振動部分隨著時間的增加而衰減，則穩態響應將僅由強迫振動的解構成。

3 解析解的相關討論

3.1 誤差分析

在k為-2，Kp分 別 為0.02和0.01時，附 錄A圖A2給出了方程（5）的數值解（采用ode45解法）與解析解的比較結果。改變鎖相環比例參數，在振蕩收斂或振蕩發散狀態時，解析解在前幾個振蕩周期皆與數值解一致。隨著振蕩誤差的累積，強迫振動的斜率在后期會出現一定的偏差。上述現象產生的原因有以下幾點。

1）由于式（5）求解困難，因此為了符合應用多尺度法的微分方程形式，用于求解解析解的式（6）是在式（5）的基礎上通過泰勒展開并舍去高階項處理得來的，從而振蕩的幅值和相位會與實際情況有所出入。當δ振蕩幅值越大時，誤差也就越明顯。此外，因為式（16）中Af與ω0有關，而ω0正是由于上述處理得來的，所以強迫振動的斜率也會與實際斜率有誤差，在2～4 s時解析解與數值解振蕩斜率分別約為-0.011 6和-0.012 6（見附錄A圖A2）。

2）解析解是一次近似解，而不是式（6）的精確解，進一步求取其二次、三次近似解，可增加解的精度。

3）當時間跨度足夠大時，由于一次函數項與正弦項誤差較大，式（7）與式（6）不再等價，此時此解析解便不再適用。

3.2 顯含時間項的二階微分方程的解

當Ω足夠小時，在一定時間范圍內式（17）成立。

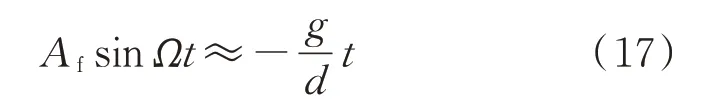
雖然非線性微分方程不滿足疊加原理，但是研究結果表明，在一定情況下，顯含時間一次項的非線性微分方程的解的形式可以看作非線性解與線性解的疊加。式（5）等號右側的一次項影響的是強迫振動的斜率。

由于鎖相環路方程有其具體的物理背景，因此也可以認為電網頻率的擾動使得電網阻抗值發生變化，δ的穩態值也在不斷地變化，因此式（18）成立。

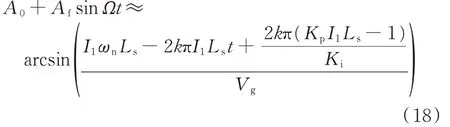
基于鎖相環路方程及其物理意義，可對解析解的強迫振動斜率進行修正。基于式（18）進行解析解修正，可以使解析解的強迫振動斜率與數值解更吻合（見附錄A圖A3）。

3.3 穩定邊界

式（5）中有顯含時間的一次項，因而δ存在強迫振動。在非共振情況下，δ是由非線性解析函數決定的自由振動與強迫振動的組合；當自由振動衰減后，就只剩下強迫振動。在非共振情況下求解穩定邊界時，解析解中的強迫振動項不會對系統穩定性造成影響。經推導，m可展開為：

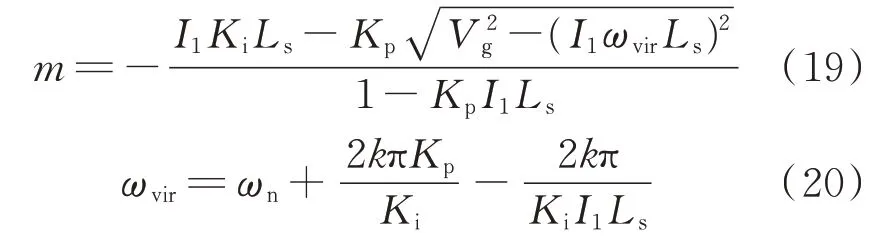
式中：ωvir為固有角頻率的修正值。

圖2（a）至圖2（d）分別給出了在Kp-Ki-I1、Kp-Ls-I1空間內m等于0時的穩定邊界曲面及幾組Ki和Ls參數下的邊界曲線。在這里將m稱作“判據值”。m小于0絕對發散，可將滿足m小于0的參數區域視為振蕩發散域，m大于0的參數區域視為振蕩收斂域。若絕對收斂還需要進一步滿足式（21）。

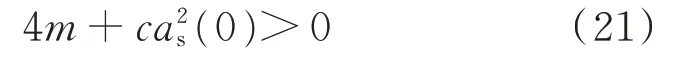
式（21）與系統初始運行狀態有關，若不能滿足，則鎖相環輸出也將振蕩發散。在圖2（a）至（d）中，隨著Kp增大，電流I1非線性增加，Ki和Ls的增大皆會使邊界曲線向下偏移。電網參數和控制參數的變化，可能使得原先的穩定點變為不穩定，如點A至點C（I1增大）、點D至點C（Kp減小）所示。解析解得到的穩定邊界可以在一定程度上指導鎖相環的控制參數設計。

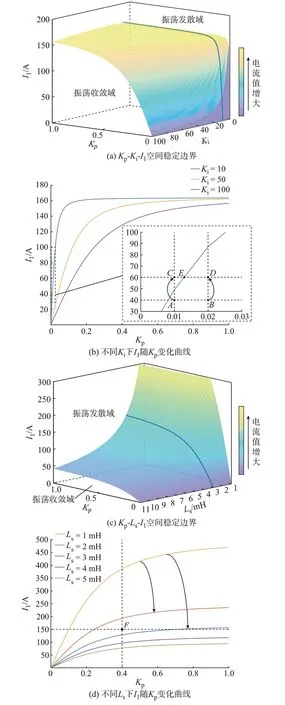
圖2 在不同空間內的穩定邊界Fig.2 Stability boundary in different spaces

4 仿真及實驗驗證

用于仿真驗證的Simulink模型參數設置如下：電網相電壓（峰值）Vg=155 V；電網電感Ls=3 mH；濾波電感Lf=1 mH；濾波電容Cf=25μF；直流側電壓Udc=380 V；直流側穩壓電阻R=0.01Ω；直流側穩壓電容C=4 000μF；電網基準頻率f=50 Hz；電流環比例系數Kip=2；電流環積分系數Kii=20。為了驗證解析判據的有效性，基于上述參數以及圖2的穩定邊界，在k=-2的前提下設置如表1所示的4種仿真驗證工況，可以得到圖3所示仿真結果以及圖4所示相圖。

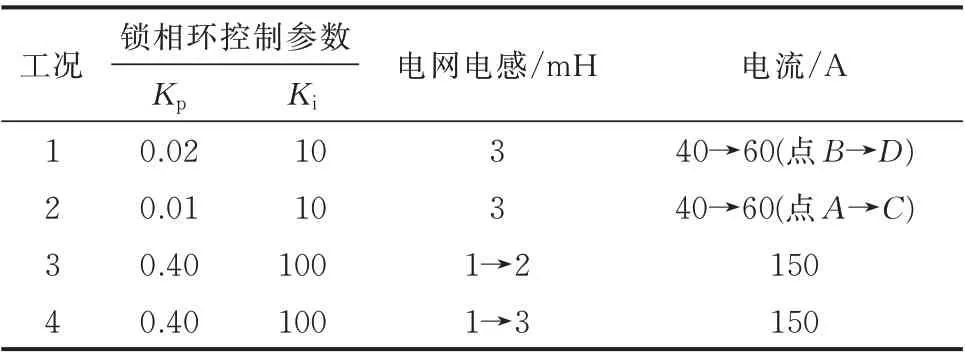
表1 仿真驗證工況設置Table 1 Settings of operation conditions for simulation verification

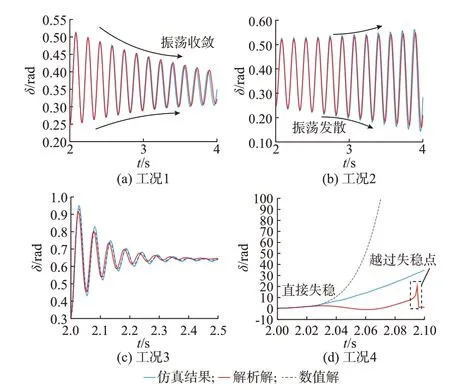
圖3 鎖相環二階微分方程一次近似解與仿真結果的比較Fig.3 Comparison of first-order approximate solutions to second-order differential equation of PLL and simulation results

圖4 鎖相環輸出相角相圖Fig.4 Phase diagram of PLL output

工況1和2設置了電流擾動，工況3和4設置了電網電感擾動。在圖2中，工況1和3均在穩定域內，工況2和4均在失穩域內。圖3（a）至圖3（d）分別給出了4種工況下的仿真結果與解析解和數值解的對比結果。由圖3可得以下結論。

1）圖3（a）中δ振蕩收斂，圖3（b）中δ振蕩發散，2種工況下解析解與仿真結果皆比較吻合；仿真收斂和發散結果與圖2穩定域判定結果一致。

2）圖3（c）中δ振蕩收斂，解析解與仿真結果的幅值誤差約為0.035 rad，周期誤差從0逐漸增大，而原始方程的數值解與仿真結果的幅值誤差約為0.017 rad，其原因可能是解析解的局限性以及仿真中電流環、開關動態等的影響；仿真收斂和發散結果與圖2穩定域判定結果一致，在這種工況下，誤差未對判別結果造成影響。

3）在圖3（d）中，解析解、數值解與仿真軌跡不相符合，但穩定判別結果與圖2一致：數值解與仿真結果不符合是因為系統失穩，電流發散，不符合所建微分方程模型的前提（即穩態點附近電流值設為固定不變）；在2.09 s左右時，δ的解析解越過不穩定點失去穩定，但由于解析解表達式中的分母存在極點，在計算過程中虛部被忽略，故出現了如圖3（d）所示越過穩定點的現象；而解析解與數值解不符合是因為擾動過大、泰勒展開的高次項被忽略引起的。

4）由圖3（a）和圖3（c）相比可知，工況3條件下δ的收斂速度較快；由圖3（b）和圖3（d）相比可知，工況4條件下δ的失穩速度較快。這與解析解的判據值m絕對值的大小相關。

解析解判穩結果與仿真結果的對比如表2所示。通過對比工況1和2或工況3和4的判據值m可以看到，在m大于0且滿足式（21）的前提下，δ振蕩收斂，且m值越大，收斂效果越明顯；在m小于0時，δ振蕩發散或直接失穩，m絕對值越大，δ發散速度越快。

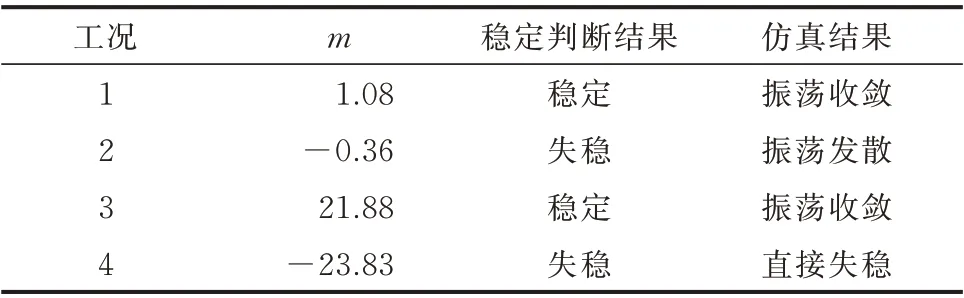
表2 4種工況下的解析穩定判斷及仿真驗證結果Table 2 Analytical stability judgment and simulation verification results under four operation conditions

圖4（a）至圖4（d）給出了4種工況下的鎖相環輸出相角相圖，其中，δ˙表示δ的一階導數。可以看到，圖4（a）和（c）中鎖相環輸出逐漸收斂，圖4（b）和（d）中鎖相環輸出逐漸發散或直接失穩，相圖結果與圖2穩定域判定結果一致。圖3和圖4結果表明，相圖分析結果與解析結果在δ的斂散性上具有一致性。

綜合以上分析：在暫態響應方面，在δ波動幅度較小時，解析解可以很好地展現鎖相環受擾時的暫態過程；當振蕩幅值較大時，因解析解本身的局限性，其與數值解和仿真結果不一致，此時從波形上看是不符合的。在判斷穩定性方面，由于穩定性和臨界狀態緊密相關，因此第1個振蕩周期的有效性即可使解析判斷穩定結果有效，而鑒于圖3（c）的誤差，可在對鎖相環進行參數設計時留有一定的裕度。m絕對值的大小可在一定程度上衡量穩定/不穩定裕度的大小。

為了進一步對穩定邊界進行驗證，對工況3和工況4進行了并網逆變器的硬件在環實驗。實驗裝置如附錄A圖A4所示，并網逆變器的主電路在RTLAB實驗平臺上建立，控制部分由DSP 28335數字控制平臺實現。圖5給出了硬件在環實驗結果。

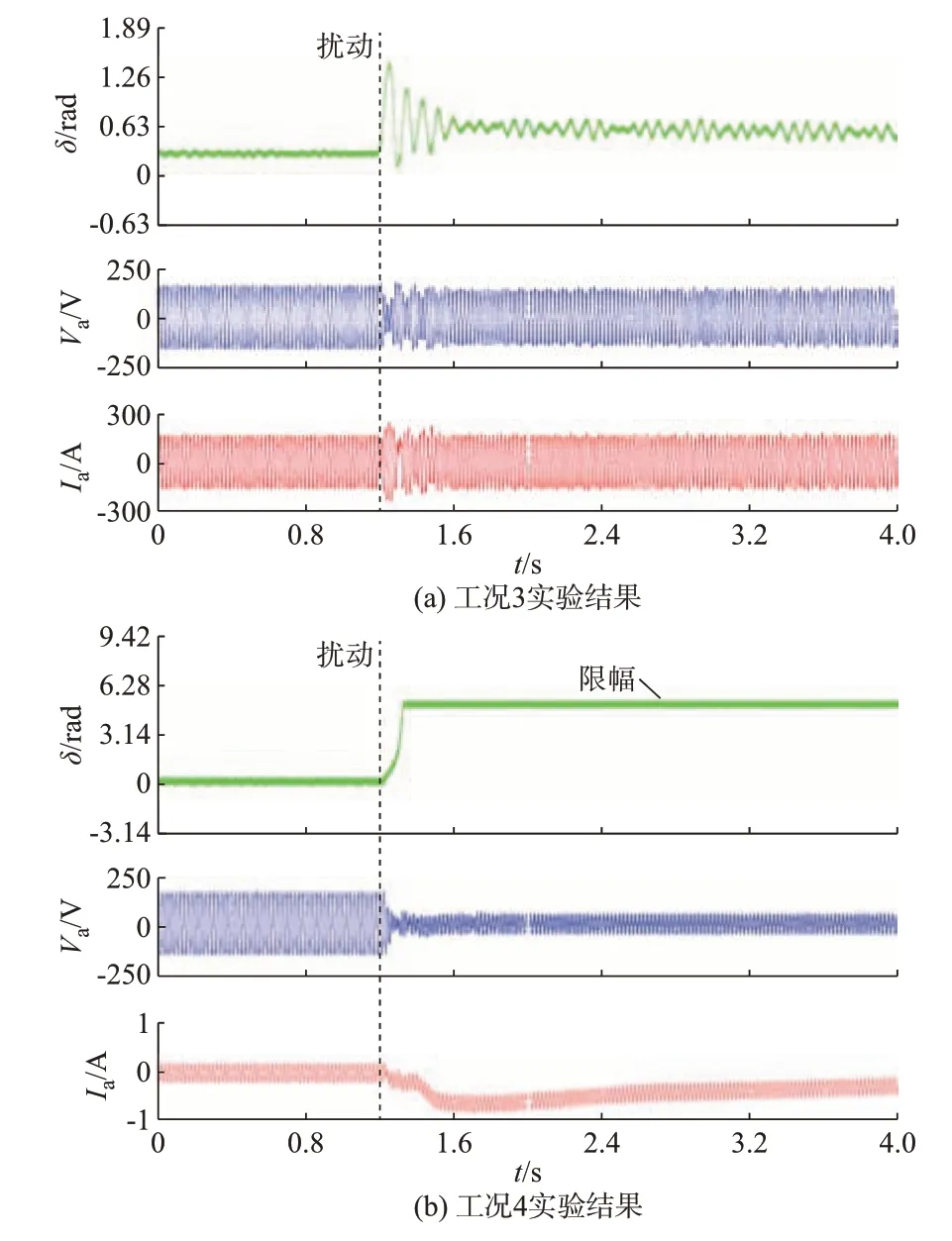
圖5 實驗驗證結果Fig.5 Results of experimental verification

圖5（a）中PCC處A相 電 壓Va和A相 電 流Ia經過振蕩恢復穩定，由于電網阻抗增大，電壓的幅值有所下降，鎖相環與電網的相角差δ在擾動后0.4 s左右穩定在新的穩態值（約0.65 rad），并進一步隨著電網頻率而變化。圖5（b）中，系統公共耦合點處電壓和電流直接失穩，鎖相環與電網的相角差δ迅速增大并達到了限幅值（約5.03 rad）。這2種工況下的實驗結果進一步驗證了穩定邊界的有效性。

5 結語

本文針對電網頻率擾動時弱電網中鎖相環輸出相角的二階微分方程，推導了解析解及穩定邊界，通過仿真及實驗，得到以下結論。

1）仿真波形及實驗結果表明，基于非線性動力學多尺度法的解析解及穩定邊界具有可行性及有效性。

2）由于求解近似解時忽略了高階項，以及對小參數進行了一次近似，相角暫態表達式存在一定誤差。但是在一般擾動下，解析解完全可以用來分析鎖相環在不同電網工況下的穩定性。

3）解析結果表明，電網阻抗、注入電流的增大導致m減小并越過臨界值，鎖相環失穩；在一定范圍內增大鎖相環比例-積分控制器比例系數、減小積分系數，有利于鎖相環的快速穩定。

本文僅針對單個變換器鎖相環進行分析，今后擬對多變換器系統鎖相環穩定性現象及原因進行分析，并在現有研究的基礎上，進一步探究多變換器系統之間的交互機理。

附錄見本刊網絡版（http：//www.aeps-info.com/aeps/ch/index.aspx），掃英文摘要后二維碼可以閱讀網絡全文。