培養學生從“感覺”到“理智”的問題分析能力

張穎

[摘 要]低年段學生做題，多半是依靠直覺經驗和機械模仿，對一些有著明顯符號化、標簽化的基礎題，他們只要認為“感覺好像是這樣”就可以得出正確答案。長此以往，學生的思維就會變得淺顯化，只有多深思“一定是這樣嗎”，才能讓思維從感性向理性延伸。

[關鍵詞]滲透;思維;感性;理性

[中圖分類號] G623.5[文獻標識碼] A[文章編號] 1007-9068（2021）23-0084-02

學生考慮問題從“感覺好像是這樣”到“一定是這樣”的轉型和進步，是為了以后的學習之路更加順當。批判性地反思教學是為了更好地改進教學策略，提出更科學的教學主張，探索更先進的教育理念。那么就事論事，當學生還在經驗直覺分析的路上蹣跚踉蹌時，對待問題都滿足于“感覺好像是這樣”的狀態，我們該如何引領學生將判斷模式向“必定是這樣”的理性形態發展呢？

一、厘清思維程序，在“簡單”中做到“不簡單”

學生在求知求學的智育進程中，思維形式是從簡單到復雜，從低級到高級，從感性到理性不斷進化的。而在簡單思維階段，學生往往靠直接經驗遷移知識以及直觀操作經驗判斷。

例如，低年段學生解決這類題目：有8盒餅干，每盒裝有6塊餅干，一共有多少塊餅干？學生往往都能正確列式，但在新授課結束后，部分教師對乘法原理就不再重視，也不再要求學生說出“為什么用6×8來計算”。因為這部分教師潛意識里認為學生會列式了，就一定是通曉算理了。事實果真如此嗎？有部分學生是憑感覺列式，讓他們分析前因后果，根本交代不出什么，而當學生一直憑感覺做題，一旦感覺失效，就會黔驢技窮，頓感迷茫。

筆者看到美國加州的一版數學教材，里面有一道簡單的數學題：“有2個木匠在建木屋，又來了4個木匠幫忙，現在一共有多少個木匠在建木屋？”教材引導學生思考4個問題：①我的目的是干什么？圈出問題;②我將怎么解決這個問題？③將我的思路整理成文;④回頭檢查，我的答案是否正確？這似乎給筆者上了一課：如果學生在做最簡單的題時，也能將所有的步驟有條理、有章法地列出來，完美展現整個思維過程，也許就可以化腐朽為神奇。

又如，面對“疫情期間小剛要買8只口罩，每只2元，一共要花多少元？如果每4只口罩裝一盒，小剛要買幾盒？”的題目時，教師不妨問一問學生：“為什么用8×2？要求要買幾盒口罩又該怎么處理？”利用問題使思維程序化，學生就會在解決問題時思考：求8只口罩的總價就是計算8個2是多少，也就是用只數×口罩的單價;求要買幾盒，就要看口罩總數里面含有幾個4，也就是用口罩總數÷每盒口罩的只數，即8÷4=2（盒）。如此一來，自然可以避免“憑感覺”“想當然”列出16÷4=4（盒）的錯誤算式了。

眾所周知，飛機起飛前要滑行一段很長的跑道，因為只有這樣才能給飛機起飛做加速準備。學生的思維訓練同樣如此，如果說中年段以后是學生思維能力發展的起飛階段，那么低年段就應該是學生思維能力的滑行階段，為后續學習提供“加速度”。

二、打破常規，鼓勵創新，從“知識取舍”向“知識運用”轉變

學生的思維潛能不容小覷，這需要教師大力培養和挖掘。但很多時候，挖掘潛力是一把雙刃劍，一方面開發思維能力，另一方面又埋沒了學生的創新能力，具體表現為：學生學習時，唯教材和教師馬首是瞻，缺乏批判精神。如何幫助學生建構自主意識，發展批判性思維呢？當務之急就是在日常教學時，善待學生的錯誤。

例如，填寫計量單位：文具盒面的面積是250（? ? ）。有學生填寫了“平方毫米”，面對這一答案，筆者卻一反常態地表揚了這名學生。

一來，這樣的錯誤有創造性，這名學生在填寫前或許還會自鳴得意：“這個面積單位我們根本沒學，其他人也許不知道有這個面積單位，管他三七二十一，姑且一試。”敢于挑戰教材權威、沖破教材桎梏是要有魄力的。

二來，正確答案可能只是刻板模仿和記憶的結果，而像這種錯誤的答案也許充滿思維含量，是學生結合了面積單位和長度單位后的對應性和衍生性行為，大膽“創造”出“平方毫米”并付諸實踐，這便是質疑精神和批判精神的生動體現。

面對這一答案，筆者表揚學生之后，便設計練習題拓展學生視域，避免一葉障目不見泰山。比如，在三年級教學完5個長度單位的內容之后，筆者帶領學生上網查詢課本之外的長度單位，進行交流展示匯報，學生深感學無止境，課本上的長度單位僅僅是度量單位的“冰山一角”，給學生打開知識的大門。之后，筆者在度量單位選擇題里特意加了一道“開胃菜”：一根胡須的直徑是70（? ? ）。學生通過對比、推理，發現課本上所學的度量單位統統不適用，此處應填一個比毫米更小的長度單位。由此釋放出強烈的信號：問題的解決有時并不是必須在典型答案中做出選擇，而是要有自己的獨立判斷以及科學根據。

有些教師會擔憂，一旦開了先河，放任學生天馬行空的想象，考試的時候很吃虧。但筆者認為，學生的思維一旦被禁錮，再想激活就很困難，從長遠的思維發展來看是值得的。再者，隨著學生獨立思考能力的加強，他們在選擇答題時會更加謹慎，沒有充足理由不會輕易下結論。

三、在辯論中促成思維走向成熟，讓“感性”與“理性”并軌

部分小學數學知識可以從感性、經驗中判斷，這符合小學數學學科的特征，但不能讓學生依賴于此種判斷方法，應當通過各種渠道追求突破和進步。

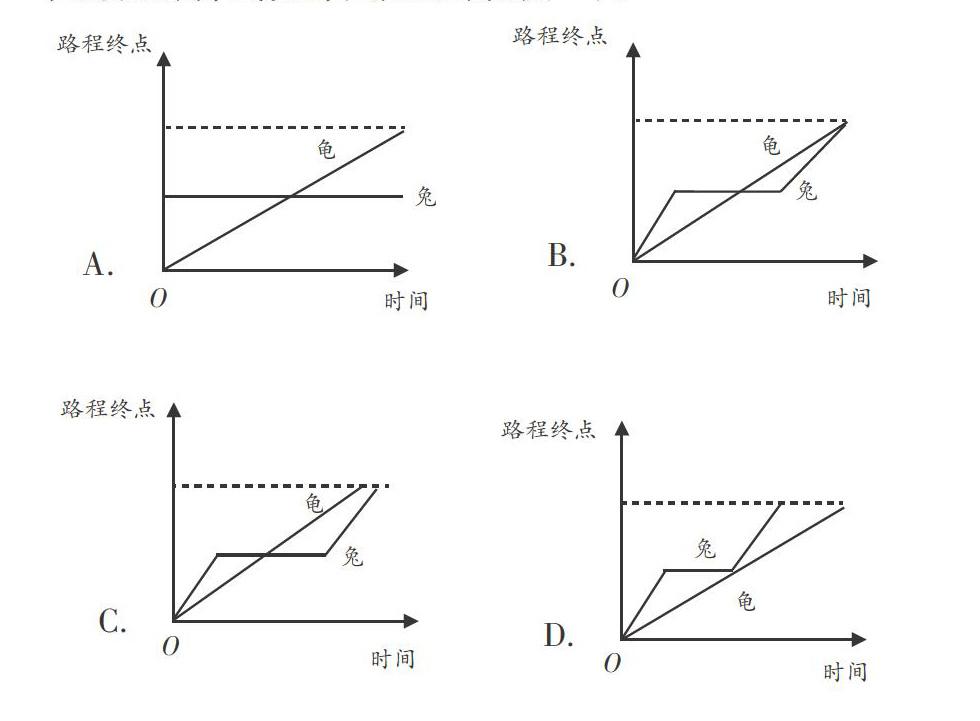
（1）在修正中“思”起來。如何讓學生慢慢學會理性看待問題？一個重要途徑就是講道理，說話有理有據。如教學折線統計圖時，出示題目“烏龜和兔子賽跑，它們同時起跑，兔子一直領先，但領先的兔子開始驕傲自滿，睡起大覺來。烏龜始終緊追不舍，當兔子睡醒時，烏龜已經反超兔子。快逼近終點時，兔子開始倒追烏龜，可是為時已晚，最終烏龜獲勝。”下列哪個選項的折線統計圖是正確的（? ? ）。

選項A是錯誤的，因為代表兔子行程的折線是水平的，且起點和烏龜不在同一位置，說明兔子在起跑點前一段距離處一直原地不動（一直在睡覺），顯然不符合劇情;而選項B的錯誤在于兔子醒來后，開始追趕烏龜，最后和烏龜同時到達終點，不符合“烏龜先到達終點”的劇情;選項D的錯誤在于最后兔子先達到終點，烏龜敗給兔子。所以正確的選項是C，而選項B具有迷惑性。本題的關鍵是要讓學生深刻理解折線統計圖表達的含義，以及各段折線表示的數量變化情況，并能將這種直觀的幾何語言轉譯成描述性語言，在與原情境對比中甄別出正確的折線圖。

（2）在辯論中唇槍舌劍。語言是思維的載體，成熟的思維需要靠精練的語言體現，讓學生在表述中進一步鍛煉思維。尤其是一些易混淆的概念，如質數和互質數概念。什么是質數？“沒有因數的自然數叫質數”這種說法漏洞百出，因為任何自然數都有因數。“除1和它本身外，沒有其他因數的自然數叫質數”這種說法才是嚴謹的，雖然有時表述起來文縐縐的，但是嚴謹精確，無懈可擊。又如，互為質數的兩個數不一定都是質數。“沒有公因數的兩個數是互質數”的說法是不嚴謹的。如自然數8和9，兩個數都是合數，但是它們卻互為質數，嚴格的說法應該是“公因數只有1的兩個數為互質數”。

數學是一門感性與理性并存的學科，學生的思維本就埋有理性的種子，當這些種子不斷萌發，就可促進理性思維的蓬勃發展。當然，對理性的追尋并不代表對感性認知的否定和排斥，感性思維中蘊含著直覺的微光，但這點微光只能照亮眼前，若要看得更遠，需要理性的追問和思考，沒有理性思維的不斷發展壯大，直覺只能是“曇花一現”。

[ 參 考 文 獻 ]

[1] 胡新猛.小學生數學問題意識培養的有效策略[J].數學教學通訊，2019（28）.

[2] 錢玲.數學問題驅動對小學數學深度學習的促進意義[J].教師，2020（18）.

[3] 董真.小學數學分析和解決問題能力的組成及培養策略解析[J].數學大世界（下旬），2019（5）.

（責編 覃小慧）