帶有特殊非線性項(xiàng)的Dirichlet問(wèn)題正解的確切個(gè)數(shù)
姚燕燕, 徐 晶, 高紅亮
(蘭州交通大學(xué) 數(shù)理學(xué)院, 蘭州 730070)
1 引言與主要結(jié)果
考慮當(dāng)非線性項(xiàng)為f(u)=u(eu-1)和f(u)=eu-1兩種形式時(shí), 一維Minkowski空間給定平均曲率方程Dirichlet問(wèn)題

(1)
正解的確切個(gè)數(shù)及分歧圖, 其中參數(shù)λ,L>0.
平均曲率問(wèn)題是偏微分方程中的一個(gè)重要問(wèn)題.設(shè)Ω?N為一個(gè)區(qū)域,k≠0是常數(shù).考慮方程
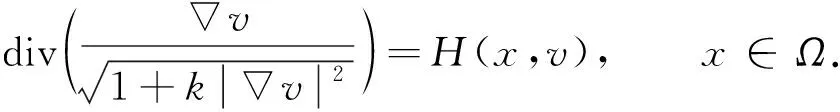
(2)
當(dāng)k=1時(shí), 方程(2)稱(chēng)為Euclidean空間中的給定曲率方程; 當(dāng)k=-1時(shí), 方程(2)稱(chēng)為Minkowski空間中的給定曲率方程.問(wèn)題(1)是Minkowski曲率方程Dirichlet問(wèn)題
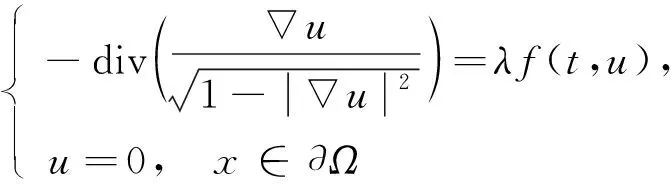
(3)
的一維情形.研究表明, 這些問(wèn)題在微分幾何和狹義相對(duì)論中具有重要作用[1-5].
近年來(lái), 關(guān)于一維或高維Minkowski空間給定平均曲率方程Dirichlet問(wèn)題的研究受到廣泛關(guān)注, 如文獻(xiàn)[6-14]用非線性分析的方法獲得了問(wèn)題(1)或(3)正解的存在性和多解性, 其中: Bereanu等[6]用Larea-Schauder度理論研究了非線性邊值問(wèn)題
(φ(u′))′=f(t,u,u′),l(u,u′)=0
解的存在性和多解性, 式中l(wèi)(u,u′)=0表示在[0,T]上Dirichlet、 周期或者Neumann邊界條件,φ: (-a,a)→是增同胚且φ(0)=0; Coelho等[7]用變分方法和拓?fù)涠壤碚撗芯苛艘痪SMinkowski曲率方程Dirichlet問(wèn)題(1)正解的存在性和多解性, 其中λ>0為參數(shù); Bereanu等[8-9]利用臨界點(diǎn)理論、 上下解方法和Larea-Schauder度理論討論了Minkowski空間中Dirichlet問(wèn)題(3)在球域上徑向正解的存在性和多解性; Ma等[10]用分歧理論研究了球域上問(wèn)題(3)正解的全局結(jié)構(gòu); Dai等[11]用分歧理論分別討論了非線性項(xiàng)在零點(diǎn)漸近線性、 次線性和超線性情形下球域上問(wèn)題(3)徑向變號(hào)解的全局結(jié)構(gòu).
上述文獻(xiàn)對(duì)平均曲率問(wèn)題正解的存在性研究較多, 而對(duì)其正解的確切個(gè)數(shù)研究較少. Zhang等[12]用時(shí)間映像原理研究了問(wèn)題
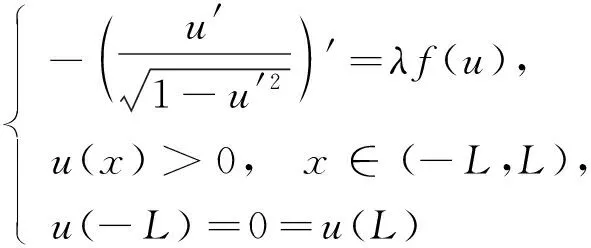
(4)
正解的確切個(gè)數(shù)及分歧圖, 其中參數(shù)λ>0,L>0, 得到了如下結(jié)果.
定理1[12]假設(shè)f滿足如下條件:
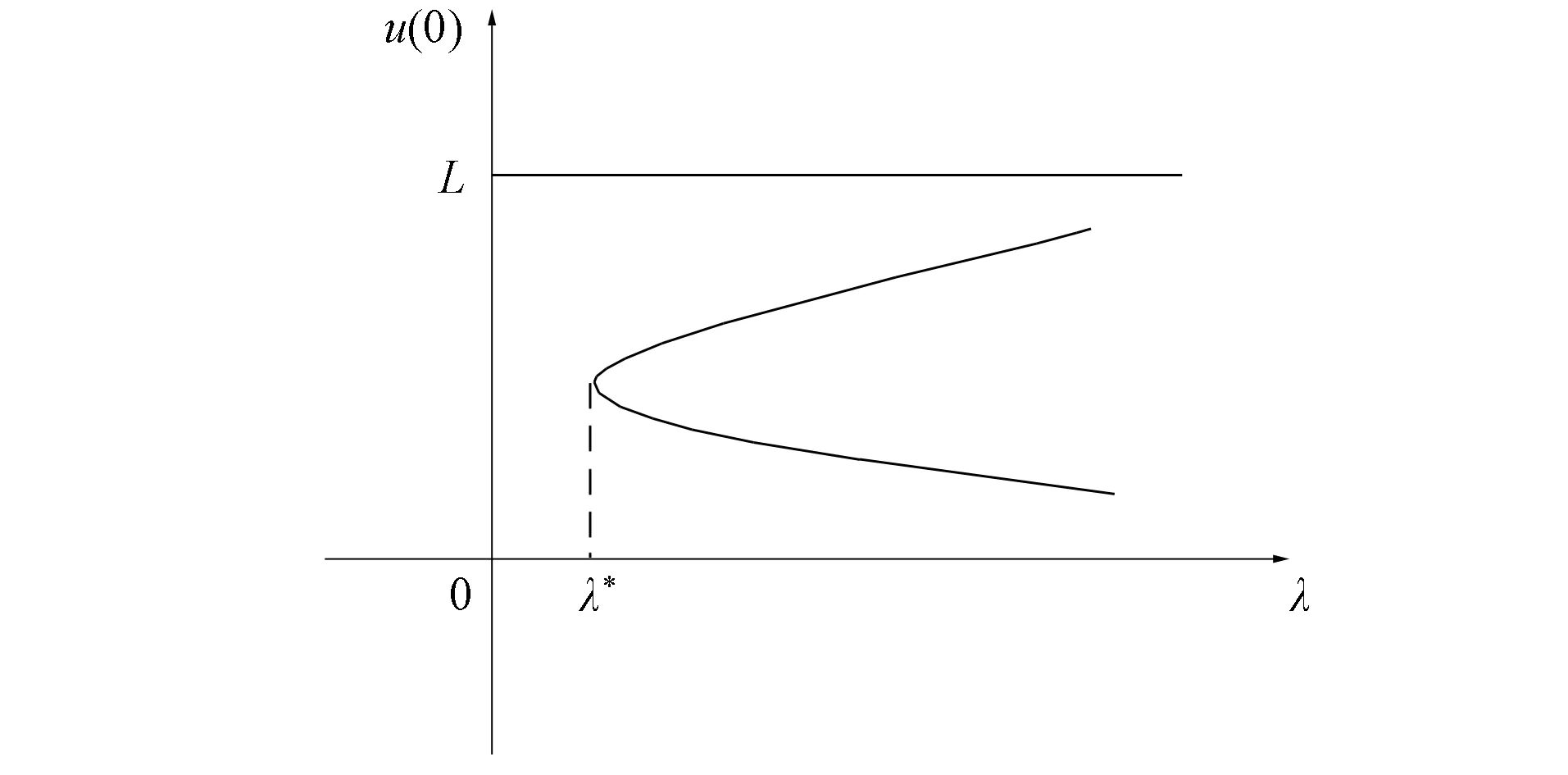
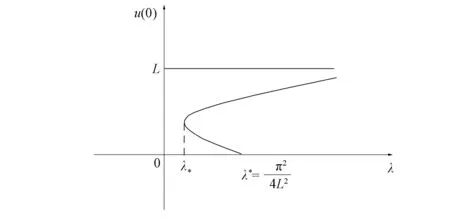
1)f∈C([0,∞),R),f(u)>0, 0 2)f∈C1([0,∞),R),f′(u)u≤f(u), 0 則有: 定理2[12]若f(u)=up(p>1), 則存在λ*>0, 使得當(dāng)λ∈(0,λ*)時(shí), 問(wèn)題(4)無(wú)正解; 當(dāng)λ=λ*時(shí), 問(wèn)題(4)恰有一個(gè)正解; 當(dāng)λ∈(λ*,∞)時(shí), 問(wèn)題(4)恰有兩個(gè)正解. 文獻(xiàn)[15-17]研究表明, 擬線性問(wèn)題與半線性問(wèn)題有很多不同之處, 分歧圖也不同.由于平均曲率問(wèn)題的時(shí)間映像估計(jì)較復(fù)雜, 因此文獻(xiàn)[12]只討論了非線性項(xiàng)在零點(diǎn)處次線性增長(zhǎng)的情形, 如f(u)=up(p>1),f(u)=up+uq(q>p>1).而對(duì)非線性項(xiàng)為f(u)=u(eu-1),f(u)=eu-1情形的研究目前尚未見(jiàn)文獻(xiàn)報(bào)道.因此, 本文研究給定平均曲率方程Dirichlet問(wèn)題(1)非線性項(xiàng)為這兩種形式時(shí)正解的確切個(gè)數(shù)及分歧圖, 其中參數(shù)λ>0,L>0.用時(shí)間映像原理獲得了如下結(jié)果: 1) 當(dāng)0<λ<λ*時(shí), 問(wèn)題(1)沒(méi)有正解; 2) 當(dāng)λ=λ*時(shí), 問(wèn)題(1)恰有一個(gè)正解; 3) 當(dāng)λ>λ*時(shí), 問(wèn)題(1)有兩個(gè)正解. 當(dāng)f(u)=u(eu-1)時(shí), 問(wèn)題(1)的分歧圖如圖1所示. 1) 當(dāng)0<λ<λ*時(shí), 問(wèn)題(1)無(wú)正解; 2) 當(dāng)λ=λ*或λ≥λ*時(shí), 問(wèn)題(1)恰有一個(gè)正解; 3) 當(dāng)λ*<λ<λ*時(shí), 問(wèn)題(1)有兩個(gè)正解. 當(dāng)f(u)=eu-1時(shí), 問(wèn)題(1)的分歧圖如圖2所示. 圖1 當(dāng)f(u)=u(eu-1)時(shí)問(wèn)題(1)的分歧圖Fig.1 Bifurcation diagram of problem (1) when f(u)=u(eu-1) 圖2 當(dāng)f(u)=eu-1時(shí)問(wèn)題(1)的分歧圖Fig.2 Bifurcation diagram of problem (1) when f(u)=eu-1 設(shè)u(x)是問(wèn)題(1)的正解.由于u(x)在x=0處取得最大值并且關(guān)于x=0對(duì)稱(chēng), 且當(dāng)-L (5) 進(jìn)而有 (6) 對(duì)式(6)兩端從0到L積分, 可得 Tλ(s)稱(chēng)為f的時(shí)間映像.由時(shí)間映像的定義可知, 問(wèn)題(1)等價(jià)于找到s∈(0,L), 使得 Tλ(s)=L. (7) (8) 引理1[12]若f: [0,+∞)→[0,+∞)是連續(xù)函數(shù), 且?u∈(0,L),f(u)>0, 則有 (9) (10) 引理2[12]若f: [0,+∞)→[0,+∞)是連續(xù)函數(shù), 且?u∈(0,L),f(u)>0, 則對(duì)任意s∈(0,L), 時(shí)間映像T關(guān)于λ嚴(yán)格遞減. 引理3[12]f: [0,+∞)→[0,+∞)是連續(xù)函數(shù), 且滿足?u∈(0,L),f(u)>0. 引理4f: [0,+∞)→[0,+∞)是連續(xù)函數(shù), 且滿足?u∈(0,L),f(u)>0. 證明: 1) 若f(0)>0, 則當(dāng)s→0時(shí), 故 故 并且當(dāng)s→0時(shí), 有 于是 引理5[12]記η(λ)=inf{Tλ(s)|s∈(0,+∞)}, 則η(λ)在(0,+∞)上遞減; 記ω(λ)=sup{Tλ(s)|s∈(0,+∞)}, 若ω(λ)≠∞, 則ω(λ)在(0,+∞)上遞減. 引理6若f(u)=u(eu-1), 則對(duì)于任意的λ∈(0,+∞), 有 ξ=λ(F(s)-F(st))=λ(ses-es-s2/2-stest+est+s2t2/2), 則 ξ′=λ(f(s)-tf(st))=λ[s(es-1)-st2(est-1)], ξ″=λ(f′(s)-t2f′(st))=λ[(es+ses-1)-t2(est+stest-1)]. 令 A=ξ=λ(ses-es-s2/2-stest+est+s2t2/2), B=sξ′=λ[s2(es-1)-s2t2(est-1)], C=s2ξ″=λ[s2(es+ses-1)-s2t2(est+sest-1)], 又 其中s[A(2+A)]5/2>0, 則 因?yàn)?/p> 令g(s)=s3+(M-3)s2+2(3-M)s+2(M-3), (g(s)es)′=s3+Ms2>0, ?M>0, esg(s)-estg(st)>0, 又因?yàn)?/p> 則 根據(jù)Taylor公式, 當(dāng)s<1/(1-t)時(shí), 有 則 對(duì)式(11)關(guān)于t求導(dǎo), 可得 g′(s)=4t3s4-(3t2+2t+1)(2M+3)s3+12(M+1)ts2+2(3-M)s, g″(s)=12t2s4-(6t+2)(2M+3)s3+12(M+1)s2,g?(s)=24s4t-6(2M+3)s3, 從而 f1(s)=-(t3+t2+t+1)(2M+3)s3+6(M+1)t2s2+2(1+t)(3-M)s+4M. 由于s3≤s2, 則有-(t3+t2+t+1)(2M+3)s3≥-(t3+t2+t+1)(2M+3)s2, 于是 -(t3+t2+t+1)(2M+3)s3+6(M+1)t2s2≥[-(t3+t2+t+1)(2M+3)+6(M+1)t2]s2, g1(t)=-(t3+t2+t+1)(2M+3)+6(M+1)t2=-(t3+t+1)(2M+3)+(4M+3)t2, 當(dāng)M=7,s∈(0,0.8)時(shí), 式(12)大于0.下面證明 (t-1)2s2es(1+t)[(t2+4t+1)s2-2(M+3)(t+1)s+4M]>0. 令h=(t2+4t+1)s2-2(M+3)(t+1)s+4M, 可知 h′(t)=(2t+4)s2-2(M+3)s,h″(t)=2s2>0, 則h′(t)單調(diào)遞增, 當(dāng)t=1時(shí),h′(t)=(2t+4)s2-2(M+3)s<0, 故h(t)單調(diào)遞減.于是 h(t)=(t2+4t+1)s2-2(M+3)(t+1)s+4M≥6s2-4(M+3)s+4M, 引理7若f(u)=eu-1, 則對(duì)于任意的λ∈(0,+∞), 有 證明: 記ξ=λ(F(s)-F(st))=λ(es-est-s+st), 則 ξ′=λ(f(s)-tf(st))=λ(es-test-1-t), ξ″=λ(f′(s)-t2f′(st))=λ(es-t2est). 令A(yù)=λ(es-est-s+st),B=λ(ses-stest-s+st),C=λ(s2es-s2t2est), 可知 其中 g(s)=2(2+M)-8M+2s2-6s+2s(2+M)=2s2+2(M-1)s+4-6M, (g(s)es)′=[2s2+2(M+1)s+2-4M]es. 從而當(dāng)0≤M≤1/2時(shí), esg(s)-estg(st)≥0, 其中 令 由時(shí)間映像的定義可知, 問(wèn)題(1)等價(jià)于找到s∈(0,L), 使得 T(s)=L. (13) 因此當(dāng)非線性項(xiàng)為f(u)=u(eu-1)時(shí), 問(wèn)題(1)的解等價(jià)于方程(13)的解. (14) 由時(shí)間映像的定義可知, 問(wèn)題(5)等價(jià)于找到s∈(0,L), 使得式(13)成立.因此當(dāng)非線性項(xiàng)為f(u)=eu-1時(shí), 問(wèn)題(1)的解等價(jià)于方程(13)的解. (15)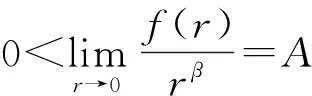
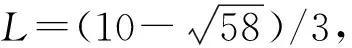
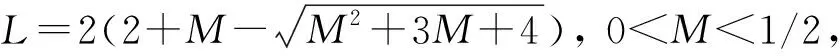
2 預(yù)備知識(shí)
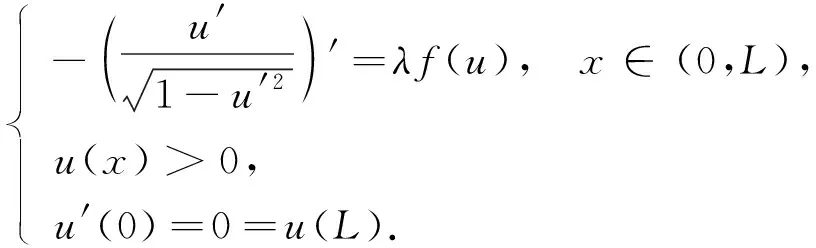
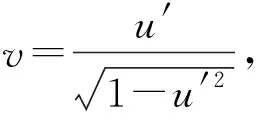

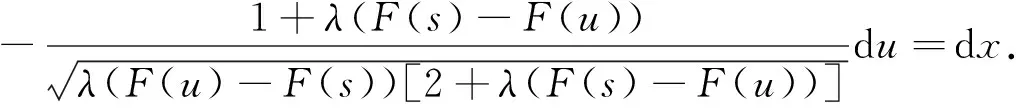


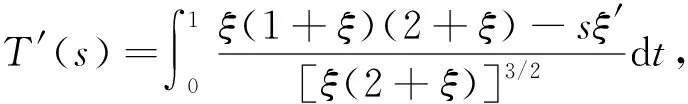
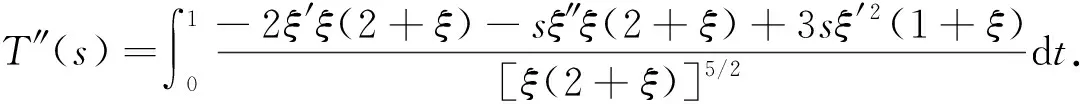
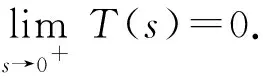
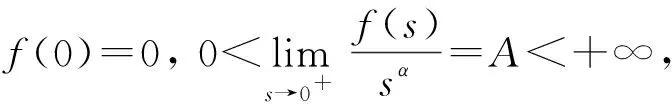

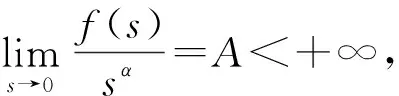
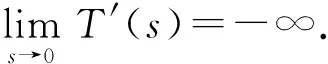
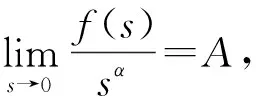
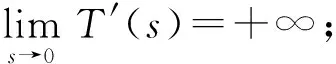
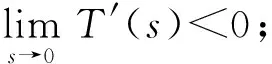
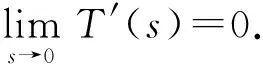
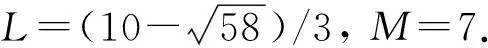
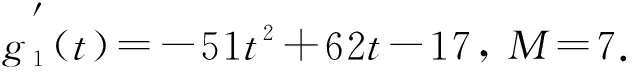
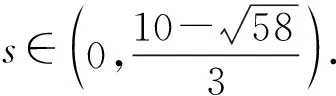

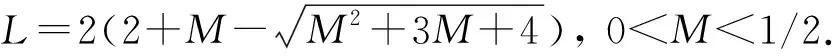
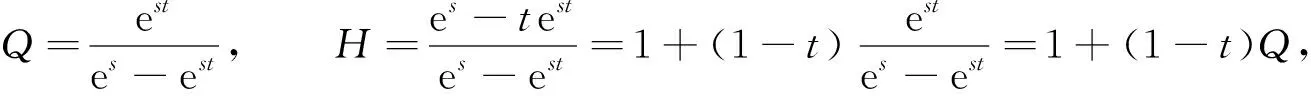
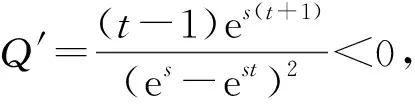
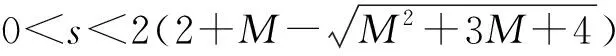
3 主要結(jié)果的證明
3.1 定理3的證明
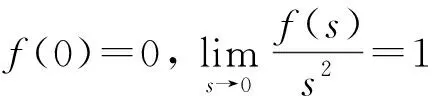

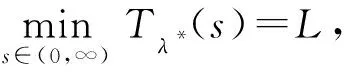
3.2 定理4的證明

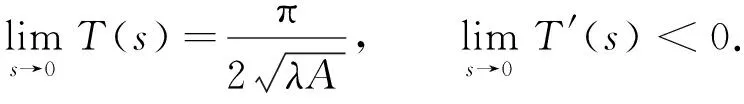
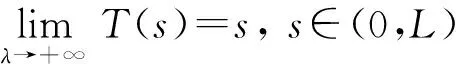
 吉林大學(xué)學(xué)報(bào)(理學(xué)版)2021年5期
吉林大學(xué)學(xué)報(bào)(理學(xué)版)2021年5期
