基于門循環單元神經網絡模型的煤層底板突水動態預測

鄧 強，張召千，王 震

(1.太原理工大學 礦業工程學院，太原 030024；2.秦皇島工程設計研究院有限公司，河北 秦皇島 066000)

煤炭是我國的戰略性能源，在貧油、少氣、富煤的能源結構下，煤炭依然會被長期依賴[1]。而在煤礦開采過程中，經常會存在大量的安全隱患[2]。其中煤層底板突水問題一直是受到專家學者關注的安全問題[3-6]。目前，煤炭開采環境復雜，煤層底板突水頻發，但突水預測能力依舊不足，對煤礦的安全生產造成了重大威脅。

國內外專家學者研究煤層底板突水問題時，會將其與煤層底板突水機理有效地結合，科學提出煤層底板突水影響因素指標體系，再通過一系列靜態預測模型，如回歸分析[7]、數據挖掘[8-9]、支持向量機[10-12]、神經網絡[13-15]及極限學習機[16-17]等方法對煤層底板突水進行預測。這些煤層底板突水預測模型在煤礦生產中的應用，提高了煤礦突水的預測能力，防范于未然。

但在煤礦的實際開采過程中，某一回采點對煤層底板突水影響是由多種因素組成的，如地質構造、煤層厚度、煤層傾角等，并且這些因素會隨著采動的進行影響權重，所以煤層底板突水預測不能簡單地當成一個靜態問題處理，需要考慮采動影響下的動態變化[18]。針對該問題，本文提出了動態預測模型：門循環單元(gated recurrent unit，簡稱GRU)神經網絡預測模型，該模型能夠充分利用采動過程中收集的時間序列數據，過濾監測過程中的缺失數據及干擾數據，通過對一系列樣本數據變化規律的學習，實時更新影響因素的變化，精確地對煤層底板突水進行預測，提高煤礦生產安全。

1 煤層底板突水指標體系

煤層底板突水是復雜的非線性問題，它受到多種因素的影響，并且隨著開采的進行其影響因素也會產生動態變化。早在20世紀60年代就有學者提出突水系數法用于煤層底板突水預測[19]。后來的許多學者不斷對突水系數法進行完善，同時，“下三帶”理論、薄板理論、“強滲通道”說及關鍵層理論等基于經驗公式和力學模型的突水理論也相繼發展起來[18]。

通過總結以往煤層底板突水理論，本文選擇煤礦突水實例的工作面煤層底板突水數據以及正常回采實測數據進行分析，如表1所示。

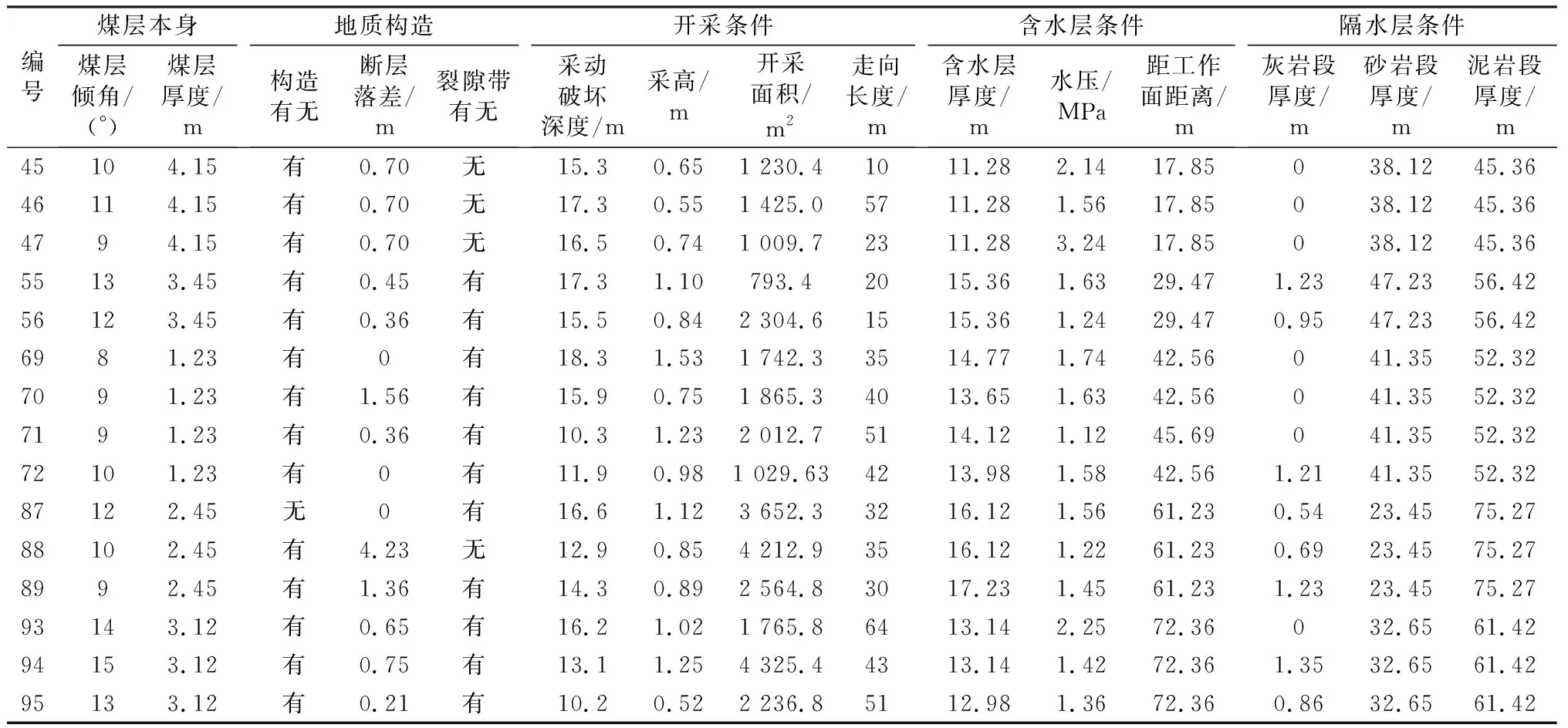
表1 礦區部分現場實測數據Table 1 Partial field measured data in mining area

影響突水的因素是多方面的，突水機理是非常復雜的，一般影響突水的因素包括地質構造、底板隔水層、底板承壓水、礦山壓力和開采活動等幾個方面。這些因素對煤礦突水影響程度各不相同，具體到某突水事故可能是單個因素的作用結果，也可能是幾個因素組合反映的作用。我們需要具體研究分析每一種因素對礦井突水的影響方式和作用，就可以有針對性地進行預測和采取有效的預防措施。

抗突水的唯一重要因素阻抗突水能力的大小取決于巖石的力學性質隔水層的厚度及其組合關系。底板承壓水對突水的影響受到水壓大小和所含水量等因素的影響，水壓是造成底板突水的前提條件和動力源泉，其作用主要是對底板巖層中的裂隙和節理進行沖刷，使得承壓水滲透量上升，當遇到不同路徑的通道接近煤層時，承壓水可能趁勢流入導致突水。除了導水斷層造成工作面突水或采掘工作揭露充水之外，礦山壓力對采煤工作面底板突水有著非常大的影響。因此，開采活動對底板突水的影響是通過對以上幾個方面的部分或綜合影響表現出來。但是隨著回采工作的進行，煤層自身及上覆和下覆巖層的原始應力狀態發生了變化，承壓含水層和底板各巖層之間所處的相對平衡狀態發生改變，其開采活動的影響正是表現在使原始的應力狀態重新分布，頂底板巖層受到破壞的過程。

本文提出了煤層底板突水影響因素指標體系，如表2所示。煤層底板突水影響因素指標體系被劃分成5個一級指標和15個二級指標。

表2 煤層底板突水影響因素指標體系Table 2 Index system of influencing factors of water inrush from coal floor

2 GRU神經網絡

數據在傳統神經網絡中傳遞是先從輸入層到隱含層，再從隱藏層進入輸出層，層間傳播呈現全連接形式，而層內的節點之間不存在聯系，模型無法很好地處理數據的時間序列問題。循環神經網絡(recurrent neural networks，RNN))的提出很好地解決了數據的時間序列問題，但RNN在計算時存在梯度消失問題，GRU的出現徹底解決了這個問題[20]。圖1為GRU神經網絡結構圖。GRU是RNN的改進版本，它在RNN的基礎上通過增加狀態c來確保在長期狀態下能夠長久保存，解決了之前僅僅一個隱層狀態h的局面。

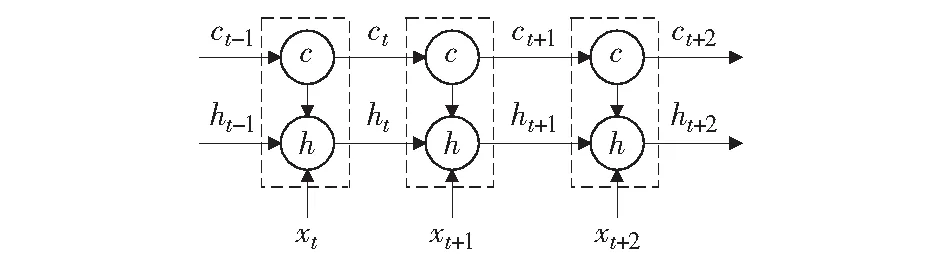
圖1 GRU神經網絡結構圖Fig.1 GRU neural network structure

圖2為GRU神經網絡模型單位結構圖。GRU單元中含更新門zt、重置門rt、輸入xt、輸出ht，t-1表示上一時刻，t表示當前時刻。重置門決定上一時刻的單元信息是否被記住或者遺忘，更新門決定單元信息是否被刪除或新信息是否被添加。隱藏層通過使用One-Hot編碼進行二維向量輸出，在隱藏層傳遞最后一個時間單元的輸出值給輸出層后，SoftMax分類器會對其進行解碼，將其轉化為代表預測結果的0和1，其中1代表突水，0代表不突水。

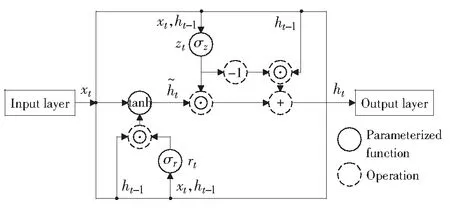
圖2 GRU神經網絡模型單元結構圖Fig.2 GRU neural network model unit structure

式(1)表示此模型的損失函數：

J(θ)=-∑(x(i),y(i))∈Dlog(p(y=y(i)|x(i),θ)) .

(1)

式中：θ為模型參數；D表示樣本數據構成的訓練集；(x(i)，y(i))表示訓練集中第i個樣本數據，x(i)是10維的向量，y(i)的取值僅有0和1，分別表示不突水和突水；p(y=y(i)|x(i))，θ)表示樣本(x(i) ，y(i))突水(不突水)的概率。

3 煤礦實測數據采集及處理

3.1 數據來源

本文研究的某煤礦含煤層為侏羅系中統延安組，根據巖性、巖相、沉積旋回及煤巖組合特征分為三段:第一段含4、4-1、4-2煤，第二段含4上-2、4上-1煤，第三段含3煤。礦井目前開采4煤層，4煤層屬于穩定可采煤層，底板為泥巖。礦區主要屬中生代承壓水盆地范疇，勘探階段未揭露大型斷層，僅在采掘過程中揭露部分小型斷層，因此該礦的充水通道主要受采動影響。

回采工作面位于礦區二采區中部。煤層頂板為深灰色炭質泥巖和灰白色中砂巖，工作面地質構造相對簡單。工作面三岔口以北263 m存在一正斷層，斷層面膠結性良好，透水性較差。三岔口以北516 m處存在一逆斷層，斷層發育高度較小，掘進過程中頂板存在淋水現象，水量較小且持續時間較短。NY103工作面中部有一走向EW的向斜構造，北翼傾向SW，傾角3°～8°，南翼傾向NW，傾角3°～11°.回采過程中頂板淋水、NY105工作面采空區積水等將全部流向向斜軸部，有可能造成工作面突水。

本文選取該煤礦突水實例的工作面煤層底板突水數據以及正常回采實測數據進行分析(如表1所示)。

3.2 數據歸一化處理

由于原始數據中各項數據相互間有較大的差別，例如其數據類型有差別、數據采用的量綱也不同、絕對值存在較大的差值，因此需要對數據進行歸一化處理，否則會對模型的運行產生較大影響。輸入樣本中包含邏輯型數據和數值型數據，前者使用0和1表示，后者運用線性轉換方式把輸入數據的范圍投射到[0，1]區間，其轉換方式如式(2)所示：

(2)

式中：x(p，i)為樣本p中第i個數據進行歸一化處理后的數值；x0(p，i)為樣本p中第i個數據進行歸一化處理前的數值；xmin(i)為全部樣本中第i個數據的最小值；xmax(i)為全部樣本中第i個數據的最大值。

3.3 基于Wrapper評價的特征選擇

特征選擇是將冗余特征去掉，將輸入向量空間維數減小，同時將學習樣本進行優化，是對輸入數據使用降維操作的一個步驟，可以明顯提升訓練效率。針對煤層底板突水預測問題，各個地區的煤礦處于不同的地理位置，并且各個地區煤礦的主控因素千差萬別，因此存在各種各樣導致突水的原因。在現場收集的數據不僅數據量非常大，同時存在許多無關緊要的冗余數據，而這些數據會對模型的訓練效率產生影響，所以需要預先去掉這些冗余數據。

在突水預測問題方面，可以采用Wrapper評價策略，因為原始樣本的數據量比較小，其數據特征只有15維，在保證準確率的情況下，運算速度也不至于太慢。因此本文選用基于Wrapper評價策略的特征選擇方法[21]。

以下為該特征選擇方法的詳細過程和計算結果：

將原始特征集合內的所有特征進行編號，開始第一輪的特征選擇，號碼“1，2，…，15”分別代表“煤層傾角、煤層厚度、構造有無、斷層落差、裂隙帶有無、采動破壞深度、采高、開采面積、走向長度、含水層厚度、水壓、距工作面距離、灰巖段厚度、砂巖段厚度、泥巖段厚度”。在15維的原始特征集合內每次刪掉號碼i的特征(i=1，2，…，15)，把剩下的14維特征用特征子集Mi(i=1，2，…，15)表示，從而獲得M1，M2，…，M15共15個特征子集；并且，用子集M0表示原始特征集合。把子集M0，M1，M2，…，M15按順序輸入模型，對GRU神經網絡模型進行訓練，將預測準確率的大小用作評判結果好壞的標準，選用“十折交叉驗證法”對錯誤率進行運算。Mi(i=0，1，…，15)的錯誤率分別由xi(i=0，1，…，15)表示。把xi(i=1，2，…，15)分別與x0做對比，如果相互間的差值很小，就假設僅去掉號碼i的特征之后，對整體的誤差率不會產生太大影響，將其認定為待定冗余特征。

圖3為各個子集第一輪特征選擇時的誤差率計算結果，由圖可知，“x0，x3，x9，x12，x15”這5個點的誤差率較低，將不去除子集中任意特征的誤差率設為x0，“x3，x10，x13，x15”代表在原始的特征子集中僅單獨去掉“構造有無、含水層厚度、灰巖段厚度、泥巖段厚度”這四個特征后的誤差率。故而，“構造有無、含水層厚度、灰巖段厚度、泥巖段厚度”被判定為待定冗余特征。同時，因為x3和x0最為相近，因此認定與其對應的“構造有無”為冗余特征，再把該特征從原始集合中剔除，集合變成14維，然后進行第二輪特征選擇。和第一輪相同，第二輪特征選擇對每個特征重新編號，重復一遍第一輪的過程。

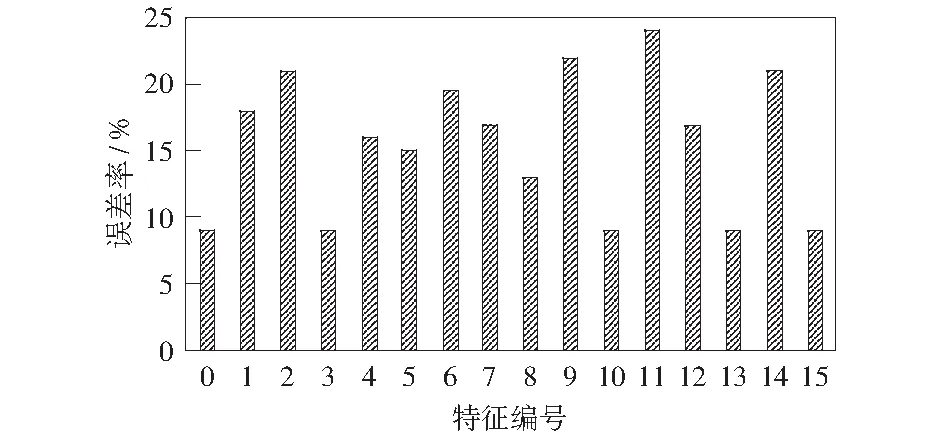
圖3 各個子集在第一輪特征選擇時的誤差率Fig.3 Error rate of each subset in the first round of feature selection

圖4為各個子集在第五輪特征選擇時的誤差率。如圖所示，從集合中單獨去除某一特征后，都顯著影響了最后的誤差率，可以表明“煤層傾角、煤層厚度、斷層落差、裂隙帶有無、采動破壞深度、采高、開采面積、走向長度、水壓、距工作面距離、砂巖段厚度”這11項特征和煤層底板突水是密切相關的。同時前四輪已去除的4項特征被認定為冗余特征，分別為“構造有無、含水層厚度、灰巖段厚度、泥巖段厚度”。

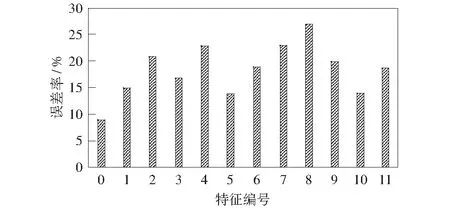
圖4 各個子集在第五輪特征選擇時的誤差率Fig.4 Error rate of each subset in the fifth round of feature selection

4 煤層突水GRU神經網絡預測模型的建立

4.1 GRU預測模型的訓練

GRU神經網絡模型可以學習時間序列數據。由上文可知，數據維數已由15維降到11維，在進行分類和劃分數據集后，就可輸入到模型中。通過回采點與時間段的差異，對數據進行排序分組，然后把分組好的數據分為訓練集、驗證集和測試集；每個部分所占的比例不同，其中訓練集是分組好的數據中隨機抽取60%所構成，驗證集為20%，測試集為20%.

在訓練過程中，每次訓練輸入一組數據，把模型預測結果和實際結果對比，從而得到誤差率，之后采用優化算法對權重矩陣進行更新，提高預測準確率。在全部數據都輸入模型得到預測結果，并進行權重調整后，對模型的一輪訓練才算結束。同時，根據實際情況確定訓練的輪數。

4.2 訓練結果分析

圖5為GRU神經網絡模型準確率及損失情況。圖5(a)代表訓練集上預測的準確率變化動態，圖5(b)表示訓練集上損失值變化動態，圖5(c)表示驗證集上預測的準確率變化動態，圖5(d)表示驗證集上損失值變化動態。因Dropout的啟用，一部分節點被隱藏，模型的準確率以及損失會隨迭代次數的加大而發生抖動，而訓練集準確率低于驗證集，同時明顯的過擬合顯現沒有發生。由圖5可以得到，GRU預測模型在訓練集上的準確率可以達90.42%，在驗證集上的準確率可以達96.29%.

圖5 GRU神經網絡模型準確率及損失情況Fig.5 Accuracy and loss of GRU neural network model

5 煤層底板突水動靜態模型預測對比

結合前文礦區的現場實測數據，本文使用支持向量機、BP神經網絡、極限學習機這三個靜態神經網絡預測模型與動態的GRU神經網絡預測模型進行對比。每個模型均按前文所述方法，將數據劃分成訓練集、驗證集及測試集，應用各模型將訓練集數據進行訓練，以測試集準確率為準進行模型預測精度評估。

不同預測模型的準確度結果如圖6所示，動態的GRU神經網絡預測模型在訓練、驗證和測試三個階段的準確率均要高于靜態的支持向量機、BP神經網絡和極限向量機。尤其是在最終的測試階段，動態的GRU神經網絡預測模型的準確率要達到95.23%，而其他的靜態預測模型的準確率均低于90%.

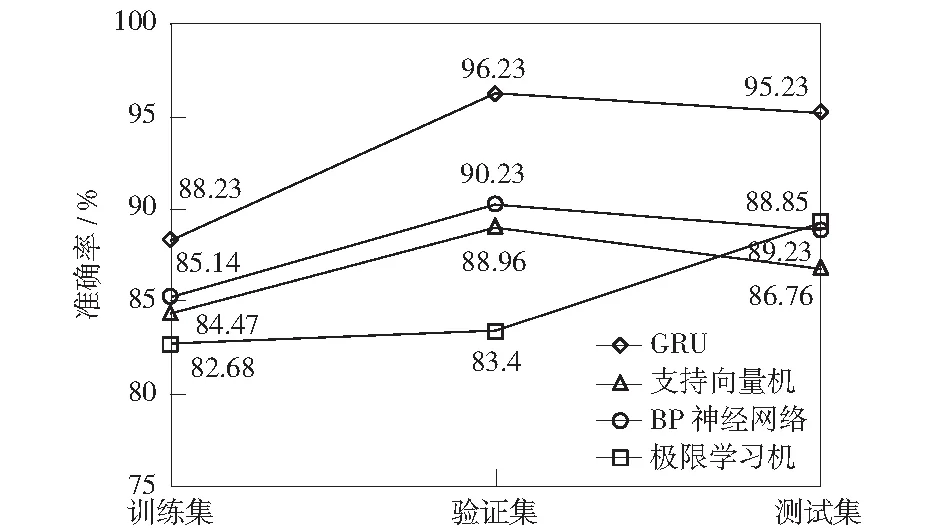
圖6 不同預測模型在訓練、驗證及測試階段的準確率Fig.6 Accuracy of different prediction models in the training, verification, and testing phases

GRU神經網絡模型與BP神經網絡等向前反饋的靜態預測模型相比，GRU神經網絡模型依靠對大量的數據樣本進行學習，并自身總結出煤層底板突水的變化規律及該動態變化對突水的影響，從而對突水變化因素進行高精度的篩選，較其余三種靜態神經網絡預測模型在煤層底板突水預測能力上具有更高的準確率，運用到煤礦開采中可以極大地提高生產安全。

工程現場表明，大部分礦井突水都與斷層、陷落柱等構造密切相關。該礦統計的大部分數據中都是有構造的，但通過Wrapper評價的特征選擇，最終確定“構造有無”為冗余特征；相反，“煤層厚度、開采面積”卻被特征選擇為與煤層底板突水密切相關。后續研究需要進一步改進相關的特征選擇方法。

6 結論

1) 以煤礦突水理論及現場實測數據為依據，建立了煤礦突水影響因素指標體系，并基于Wrapper評價策略的特征選擇，確定“煤層傾角、煤層厚度、斷層落差、裂隙帶有無、采動破壞深度、采高、開采面積、走向長度、水壓、距工作面距離、砂巖段厚度”這11項特征和煤層底板突水密切相關。

2) 煤層突水GRU神經網絡模型通過對現場實測數據的學習，確定其在訓練集上的預測準確率達90.42%，在驗證集上的準確率達到96.29%，可以很好地進行煤層突水預測測試。

3) 將動態的GRU神經網絡預測模型與支持向量機、BP神經網絡及機器學習機這三個靜態的神經網絡預測模型進行比較，發現動態的GRU預測模型預測的準確率在訓練、驗證及測試階段都要高于其他的靜態模型。因此，GRU模型比其他靜態神經網絡預測模型要更適合應用到煤層底板突水預測。