四階精度差分法解定態薛定諤方程

劉展源，關成波，呂英波，張 鵬，叢偉艷

(山東大學(威海) 空間科學與物理學院，山東 威海 264209)

在經典物理場方程的數值求解中，差分法是一種最普遍采用的方法[1-3]．通過自變量的離散化，差分法把微分方程轉化成代數方程，其中最重要的是將待求函數的導數用有限差分近似表示．文獻中，各類精度差分公式的推導一般是利用待定系數法，結合泰勒級數轉化成線性代數方程組的求解．本文介紹一種更簡潔的方法，利用多項式插值導出差分公式，包括二階精度和四階精度差分公式．這種方法既易于理解也方便推廣到更高的維數和精度．

差分法也經常被應用于定態薛定諤方程的求解，例如一維方勢阱、拋物勢阱、W形勢阱以及各類量子阱和量子點等物理問題的研究[4-17]．對于能量分立的束縛態，差分法將定態方程轉化成矩陣的本征方程，進而求出能量和波函數的數值解．在上述研究定態問題的文獻中，普遍采用的差分公式是3點中心差分公式，其誤差為步長的二次方量級，無法滿足高精度要求．本文采用四階精度的差分公式，求解幾個經典勢場中的定態方程．以一維諧振子為例，我們利用不同精度的差分公式分別計算能級，所得結果表明，四階精度差分比二階精度差分收斂更快并且誤差更小．此外，我們還討論了兩類有限深勢阱，方勢阱和拋物勢阱，計算了不同勢阱深度下的基態能量和波函數，繪出了兩個勢阱的基態能量和勢阱深度的關系曲線．

1 插值法推導差分公式

假設待求函數f(x) 在區間 [a,b] 上是光滑的，取步長h將區間N等分，我們就可以將自變量離散化為一組等間距的節點 {xi=a+i×h;i=0,1,…,N}．數值求解微分方程就是計算出所有節點處的函數值f(xi)，而前提是將方程中的導數用有限差分近似表示．在本節中，我們利用多項式插值法推導出一階導數和二階導數的差分公式．

1.1 二階精度差分公式

如圖1所示，我們選取xi及其最近鄰的兩個節點做3點插值，可得二次多項式．

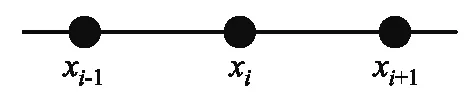
圖1 3點插值

利用拉格朗日插值公式[1,3]可以直接寫出這個多項式:

(1)

(2)

(3)

這兩個式子就是常用的3點中心差分公式，其精度可以結合泰勒級數來分析．將f(xi±1)=f(xi±h) 展開成泰勒級數:

(4)

再代入到中心差分公式(2)和(3)的右側，可得

(5)

(6)

可見，兩個中心差分公式的精度為2階，其截斷誤差為步長的二次方量級O(h2)．

1.2 四階精度差分公式

如圖2所示，我們取xi及相鄰節點做5點插值，可得4次多項式.

圖2 5點插值

其拉格朗日插值公式如下

p4(x)=

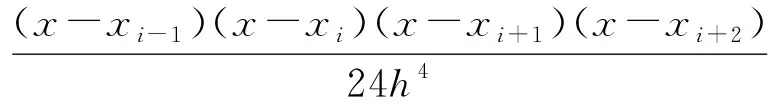
(7)

(8)

(9)

將f(xi±2)=f(xi±2h) 展開成泰勒級數:

其他應收、應付款業務是指電力企業在主營收付款業務之外發生的其他各類往來款項，包括日常供電應收的違約金罰款、對外出租包裝物等的租金、收取的職工墊付款、其他各類為政府部門等的墊付款等。根據會計核算規則，需要設置“其他應收款”“備用金”等科目。

(10)

再與f(xi±1) 的泰勒級數式(4)一起代入到5點差分公式(8)和(9)的右側，可得

(11)

f(2)(xi)+O(h4)

(12)

可見，5點差分公式(8)和(9)的精度比前面的3點中心差分(2)和(3)高了兩個階次．我們如果利用這兩個四階精度的差分公式求解微分方程，原則上可以將計算誤差控制在更小的量級．

2 差分法求解定態方程

差分法可以將定態薛定諤方程轉化成實對稱矩陣的本征方程，而求解線性代數方程有經典的算法和軟件(例如MATLAB)．本節第1部分以一維諧振子為例說明差分法的應用，利用二階精度和四階精度差分公式做計算并對比其結果．在第2部分，我們利用四階精度差分公式計算有限深方勢阱和有限深拋物勢阱的基態能量和波函數．

2.1 一維諧振子

一維諧振子的定態方程一般寫成如下形式:

(13)

(14)

諧振子的定態都是束縛態，位置概率分布集中在原點的附近．對于能級不是很高的態，可以在有限區間 [-L,L] 內求解方程，并設定邊界條件：

ψ(x)=0,|x|≥L

(15)

選取步長h將區間N等分，我們得到一組節點 {xi=-L+i×h;i=0,1,…,N}．考察節點xi處的定態方程，并將波函數的二階導數用差分公式近似，于是得到定態方程的差分格式：

(16)

也可以寫成矩陣的形式：

AΨ=EΨ

(17)

(18)

表示波函數在內部節點處的值；A為 (N-1)×(N-1) 維的實對稱矩陣，其矩陣元Aij與二階導數差分公式相關：

1) 如果選取二階精度差分公式(3)，則有

(19)

2) 如果選取四階精度差分公式(9)，則有

(20)

取區間上限L=10，對不同精度的差分公式給出的A矩陣 (19)和(20)，我們分別求解其本征方程(17)，列出前十個能級的數值結果，并與真值En=n+1/2 對比．

如表1所示，相同步長下得到的計算結果，四階精度差分明顯優于二階精度的中心差分．特別地，四階精度差分在步長為0.1時的計算結果已經非常接近于中心差分在步長為0.01時的計算結果，說明前者比后者收斂更快．

表1 一維諧振子的能級(小數最后一位四舍五入)

2.2 一維有限深勢阱

設一個質量為μ的粒子在寬為a深為V0的一維有限深勢阱中運動．為了數值計算方便，我們仍然選取自然單位，μ=a=?=1，此時能量的單位為ε=?2/μa2=1．如圖3所示.

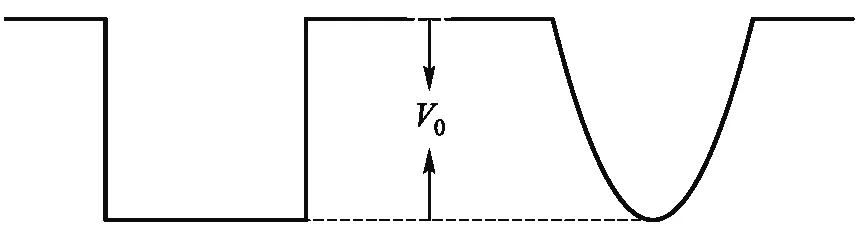
圖3 有限深方勢阱和有限深拋物勢阱

我們討論兩類有限深勢阱，方勢阱和拋物勢阱，對應勢函數有如下形式:

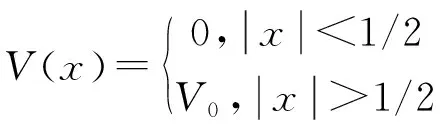
(21)

(22)

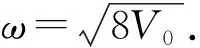
為了數值求解束縛定態，特別是基態，我們取有限區間 [-L,L]，以及式(15)中的邊界條件．勢阱如果不是很深，其束縛粒子的能力較弱，那么基態波函數的分布范圍較大，這時L要適當取稍大數值，確保波函數滿足邊界條件．我們利用四階精度差分公式分別計算了兩類勢阱的基態波函數和能量．以下是計算結果及討論．

圖4給出了不同V0時基態粒子的位置概率分布曲線，其中實線表示方勢阱中的概率分布，虛線表示拋物勢阱中的概率分布．V0取值較小時，粒子在勢阱外部的概率分布較大，有顯著的隧道效應；V0取較大值時，粒子幾乎完全被束縛在勢阱內部．另外，對比兩類勢阱中的概率分布，我們發現，在V0取值0.1和1時，拋物勢阱中的概率分布要比方勢阱中的概率分布稍寬一些，而在V0取值10和100時卻情況相反．原因在于，當V0很大時，勢阱內的拋物勢斜率也大，從而阻礙粒子向阱壁運動；當V0較小時，拋物勢斜率也小，對粒子的運動影響較弱，但拋物勢阱相對于方勢阱有更大些的基態能量，從而提高了隧道穿透的概率．

圖4 基態粒子的位置概率分布(已歸一化)

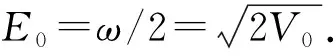
圖5 基態能量與勢阱深度 V0 的關系圖

3 結論

本文介紹了利用多項式插值推導差分公式的方法．本方法既可以推導出精度更高的差分公式(例如用七點插值)，也可以推導出任意階導數的差分公式．當然，差分公式的精度越高，計算量也會越大，我們需要結合實際情況選擇最合適的差分公式．

在差分法求解一維定態薛定諤方程時，我們建議選擇四階精度的差分公式，因為其計算量并不比二階精度的差分公式大太多，但能把計算精度提高兩個階次．