用變分優化正交的連帶Laguerre基函數計算無支撐單層MoS2中激子的能量和波函數

吳曙東, 王 強, 程立文

(揚州大學 物理科學與技術學院, 江蘇 揚州 225002)

近年來，具有二維層狀晶體結構特征的過渡金屬硫族化合物(化學式為MX2，其中M=Mo、W 等; X = S、Se或Te)因其獨特的電學和光學性質而激起了人們的極大研究興趣，在光電領域中具有廣闊的應用前景[1-7]. 以單層MoS2為代表的過渡金屬硫族化合物是一種新型的類石墨烯二維層狀材料，在位于布里淵區K和K′點的導帶和價帶之間有1.9 eV的直接帶隙，這對光電應用至關重要[7]. 此外，單層MoS2的谷圓偏振光獨特的選擇吸收允許有效地控制其自旋和谷自由度[8]. 激子是電子和空穴在靜電庫侖力作用下相互吸引的束縛態. 以前的理論和實驗結果表明，激子效應在決定單層MoS2的光學性質方面起著重要作用. 在室溫下可以觀測到不同于塊體材料高達幾百毫電子伏的激子束縛能，并且可以觀測到更高階的激子態。除了極大的激子束縛能之外，還有強激子吸收. 例如，在單層MoS2中觀察到非常強的直接躍遷光致發光. 與塊體材料相比，其發光量子效率顯著提高了104倍以上[7]. 研究結果還表明，在單層二維材料中，激子的靜態介電函數不再是定值，而是隨著主量子數的變化而變化，其來源于介質的介電屏蔽效應[3,9,10]，因此其能量本征值問題沒有解析解.在準確對角化方法中，選擇合適的基函數是很重要的.連帶Laguerre基矢是高度局域化和靈活的基函數，并且已經被證明是高精度計算的一個很好的選擇，因為它們是正交的，并且比類氫軌道和高斯型軌道收斂更快[11]. 在變分優化下，連帶Laguerre基矢僅幾個簡單的軌道就可以收斂，具有豐富的物理意義，然而其它的基矢是基于大量的基函數，使描述復雜化. 本文將以無支撐單層MoS2為例，采用了一種基于變分優化的正交歸一化的連帶Laguerre基矢的準確對角化方法計算了單層MoS2中A型激子的能量和波函數，其中哈密頓量的矩陣元中不涉及顯式積分. 通過對收斂性的檢驗和文獻數據的比較來評估該方法的收斂效率和有效性.

1 理論模型與計算方法

激子是一個因庫侖吸引力束縛在一起的電子-空穴對.在有效質量近似下，在單層MoS2中激子的哈密頓量可寫為

(1)

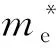
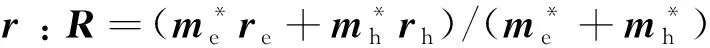
(2)

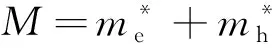
(3)

除非特別說明，本文中使用Rydberg(里德堡)原子單位(e2=2，?=1，μ=1/2)。在單層MoS2材料中，激子是在一個二維平面內運動.在極坐標(r,φ)中，電子-空穴對相對運動的薛定諤方程為

(4)

其中E和ψ(r)分別為激子的本征能量和對應的本征函數.在二維激子系統中，使用由Rytova-Keldysh導出的屏蔽庫侖勢[12]：

(5)

其中H0和Y0分別為零階Struve函數和第二類Bessel函數，r0為單層MoS2的激子介電屏蔽長度.

對于屏蔽庫侖勢，其本征值問題沒有解析解. 因此，采用變分優化的準確對角化方法求解方程(4)，將激子波函數展開為一組二維正交歸一化的連帶Laguerre基函數[11]

(6)

其中

(7a)

和

(7b)

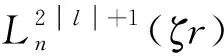
將式(6)代入式(4)，得到關于Cnl的本征值方程

(8)

其激子哈密頓量矩陣元有如下的形式

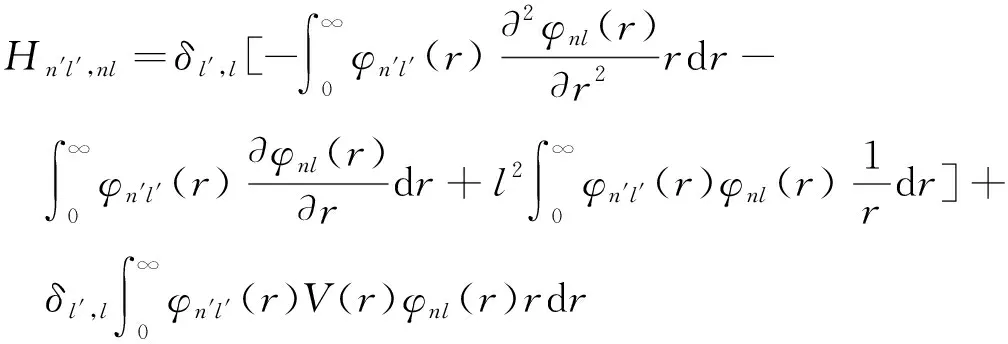
(9)

其中δn′,n和δl′,l是Kronecker delta函數. 從式(9)可以看出n不再是好量子數, 但l仍然是好量子數，因此激子本征態可根據l來分類.

為了使Hn′l′,nl中不涉及顯式積分，我們推導了激子哈密頓量矩陣元的解析形式. 連帶Laguerre多項式由以下公式顯式給出[11]

(10)

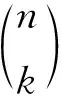
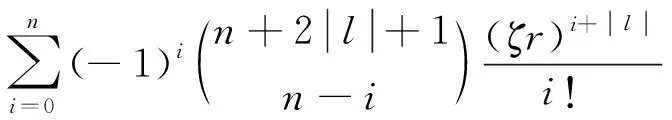
(11)

在式(9)中基于連帶Laguerre基函數積分是可積的. 對于l′=0和l=0的情況,Hn′l′,nl可寫為

(12)

對于l′≠0 或l≠0的情況,Hn′l′,nl可寫為

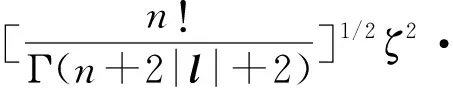
(13)

激子哈密頓量矩陣元的解析表達式大大簡化了計算，因為大部分計算時間都花費在激子哈密頓量矩陣對角化上，而不是矩陣元素的計算上.激子哈密頓量矩陣是實的，對稱的，稀疏的.在計算了激子哈密頓量矩陣后，采用變分優化的對角化方法得到激子本征能量和其對應的本征函數.在選定基函數大小的情況下， 用里茲變分原理通過改變ζ的值使能量最小化.因此，其步驟如下:

1) 初始化各能級Enl的變分參數ζ的值；

2) 將本征值方程(8)對角化得到能級Enl和波函數ψnl(r,φ)；

3) 調整參數ζ的值并跳到步驟(2)，直到找到了能量最小值Enl, 此時即為基態和激發態的能級Enl和波函數ψnl(r,φ).

2 計算結果與討論

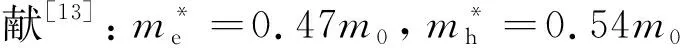
(14)

圖1所示為變分參數ζ和相對誤差ε(N)隨基矢大小N的變化情況.如圖1(a)所示，當N從3連續變化到20,ζ值顯示出隨著N增加而顯著增加的階梯狀行為. 這是因為隨著N值的增大, 展開的基函數的數量增加. 隨著ζ值的增大, 基函數被徑向壓縮. 通過變分壓縮徑向波函數而移動節點位置以獲得所需要的波函數. 如圖1(b)所示, 相對誤差ε隨N增大呈指數遞減的階梯狀行為, 這意味著相對于N的收斂速度非常快，表明了該方法的可靠性. 激子本征能量即使在少數基函數下也表現出非常好的收斂性. 例如，一個基矢大小為N=5的所有能量的相對誤差均低于10-5, 這是因為連帶Laguerre基函數在空間中非常集中，導致了相當快的收斂速度. 此外，還可以通過選擇一個最合適的ζ值對收斂性進行變分優化. 綜上所述可得出如下的結論：在基矢的大小足夠大的情況下，可獲得極好的結果. 因此，我們提出的變分優化二維正交歸一化的連帶Laguerre基矢是一個很好的選擇.

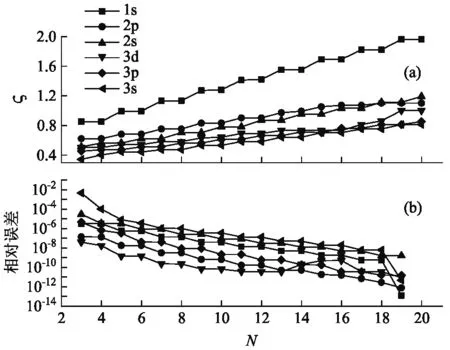
圖1 (a)變分參數ζ和(b)激子本征能量的相對誤差ε(N)隨基矢大小N變化關系

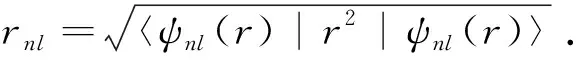
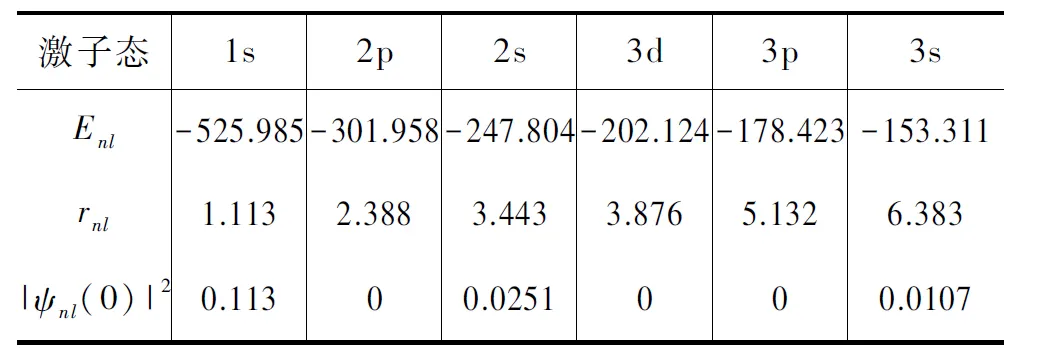
表1 在單層MoS2中，激子的6個低本征能量Enl (meV)、半徑rnl (nm)和模的平方|ψnl(0)|2

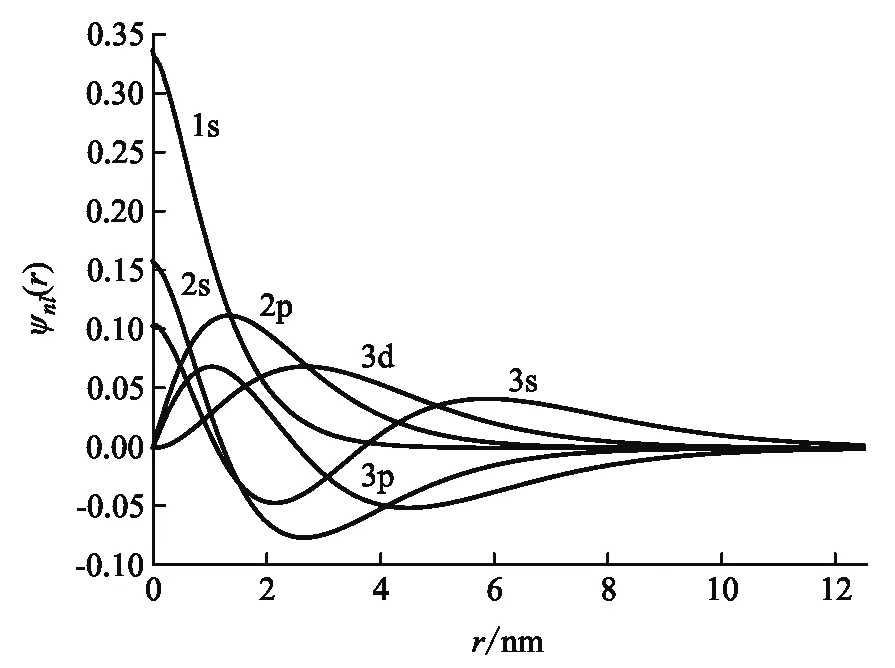
圖2 在單層MoS2中激子歸一化的徑向波函數ψnl(r)

圖2描繪了A型激子的6個低本征能量的歸一化徑向波函數. 由于V(r)圓對稱性, 我們可以把激子波函數分解成徑向波函數和角度波函數. 徑向波函數依賴于n和l. 在開區間的(0,∞)的節點數為n-|l|-1. 每次隨著量子數n增加, 一個額外的節點產生. 每次隨著量子數|l|增加, 一個額外的節點又一次消失，被通過原點的節點所代替. 1s軌道在原點有一個凸起，而它在較大距離處呈指數衰減. 它的最大值在r=0, 即為發現電子和空穴在同一空間位置的概率密度最高的點. 由于離心力項的作用，2p或3d軌道被推離原點更遠, 即?2l2/2μr2是一種排斥力。2s或3p軌道包含一個正振幅和一個負振幅. 3s軌道在3個凸凹下變得更加分散. 這是因為隨著n的增加，波函數從原點延伸得更遠，包含更多的節點.

3 結論

本文基于變分優化的二維正交歸一化的連帶Laguerre基矢，用準確對角化方法計算了無支撐單層MoS2中A型激子的本征能量和本征函數. 介電屏蔽效應破壞了SO(3)對稱性，導致了激子本征能量以反常軌道角動量的順序出現. 在變分參數優化下，分析了當基函數的大小從3連續增加到20時，激子本征能量的收斂性. 收斂速度不僅與基函數的數量有關，而且與變分參數有關. 在變分優化的情況下，收斂速度非常快，證明了該方法的可靠性. 該方法用連帶Laguerre多項式自動構造了既滿足束縛態又滿足連續態的正交基函數集，且哈密頓量的矩陣元不涉及顯式積分. 利用正交歸一化的連帶Laguerre函數作為基函數，可以顯著減小基矢的大小. 激子本征能量即使在少量基函數情況下也與以前的計算結果非常吻合. 因此，我們提出的變分優化的二維正交化歸一化的連帶Laguerre基函數是描述二維材料中激子和原子物理的一個很好選擇.