姿態傳感器的坐站轉移測量系統研究

劉 鵬，陳寶亮，肖飛云，王 勇

(合肥工業大學 機械工程學院，合肥 230009)

坐站轉移運動是人類最基本的功能性活動，是人類獨立進行日常生活活動的基本前提[1-2]，從生物力學的角度來看，坐站轉移運動需要不同肌肉之間的相互協調，以及需要足夠的肌肉力量提升身體重心運動；對于腦卒中偏癱患者而言，坐站轉移能力是決定其能否獨立生活的重要功能基礎[3]。因此，對于坐站轉移能力的評估顯得尤為重要。在臨床上，關節力矩是評估坐站轉移能力的常用指標[4]，在康復訓練器材的設計上，關節力矩對于驅動器的選擇具有重要意義。近年來一些學者也開始了坐站轉移運動輔助訓練器材的研究[5-7]，然而，建立一個有效的人類日常活動的動力學模型是設計殘疾人輔助裝置的關鍵步驟[8]。因此，分析人體坐站轉移運動對于康復評估和康復訓練器材的設計顯得至關重要。

在人體生物力學的研究中，三維運動捕捉系統通常被認為是人體運動分析的黃金標準，Pinheiro C等[9]通過運動捕捉系統和測力板對人體坐站轉移進行了運動學和動力學分析；Yoshioka S等[10]通過運動捕捉系統對人體坐站轉移的運動學和關節最小峰值力矩進行了研究；Shia V等[11]研究了基于攝像系統的坐站轉移的事件檢測，然而基于攝像機的運動捕捉系統雖然測量精度高，但是價格昂貴，測量環境要求高，只能在特定的實驗室內進行。近年來，傳感器技術的進步使小型和低成本的可穿戴設備得以迅速發展，這些設備具有復雜的功能來監測人體的運動。例如，李元良等[12]研究了一種基于MEMS(micro-electro-mechanical system)傳感器的人體運動識別系統；Kong A等[13-15]實現了基于三軸加速度傳感器的人體跌倒的檢測；劉坤等[16]通過可穿戴傳感器和測力板分析了人體坐站轉移的動力學特性，并與運動捕捉系統進行比較，然而其傳感器必須安裝在人體體段的質心位置，難以實現實際安裝。目前，基于姿態傳感器來分析人體運動的相關研究較少，姿態傳感器能夠精確測量載體的姿態角，其內部包含了三軸陀螺儀、三軸加速度計、地磁場傳感器，采用高性能的微處理器和先進的動力學解算與卡爾曼動態濾波算法，能夠快速求解出模塊當前的實時運動姿態，這對于人體運動分析提供了便利。

通過以上文獻分析，在人體坐站轉移的運動研究中，現有方法大都采用運動捕捉系統采集人體的關節角度信息。基于攝像機的運動捕捉系統價格昂貴，反射標記的安裝耗時長，對于安裝位置要求較高，而且容易被遮擋，同時需要專用的實驗室空間，后處理(包括反射標記的識別、跟蹤、空間坐標的計算)時間長，不適合作為一種臨床的技術手段。

因此，為解決上述技術問題，基于多個姿態傳感器解算人體在坐站轉移運動過程中踝關節、膝關節和髖關節的運動角度，通過建立簡化的人體動力學模型，將理論計算得到的足底壓力信息與測力板測得的實際數據進行了對比，驗證基于姿態傳感器的坐站轉移測量系統的準確性與有效性，并利用拉格朗日方法對坐站轉移運動進行動力學分析。

1 運動學信息采集及動力學建模

1.1 運動模型的建立及參數獲取

對人體坐站轉移的運動進行分析，首先需要將人體簡化為適當的計算模型，再運用坐標變換的數學方法解決人體運動位姿的計算[17]。本文研究人體坐站轉移的運動學信息，不考慮上肢和頭部姿態，所以將頭部、上肢和軀干簡化為一根連桿，假設人體坐站轉移的運動是關于矢狀面對稱的且只在矢狀面內運動[18]，足部始終與地面接觸且不發生相對運動，把左右小腿和大腿均用連桿表示，故將人體簡化為三連桿模型，三連桿之間通過轉動副連接。

簡化的人體三連桿剛體模型如圖1所示，按照右手定則，定義姿態傳感器的慣性坐標系W，在足部建立全局坐標系{OXYZ}，坐標原點O位于踝關節處，規定Y軸垂直于地面向上，X軸水平向前，在小腿、大腿和軀干分別建立局部坐標系{oixiyizi}，i=1，2，3，坐標原點分別位于踝關節、膝關節和髖關節處，如圖1中所示，yi由關節i指向關節i+1，xi垂直于yi向前，規定關節角度θi為yi與X正方向的夾角；其中關節角度θi通過如下方法計算：

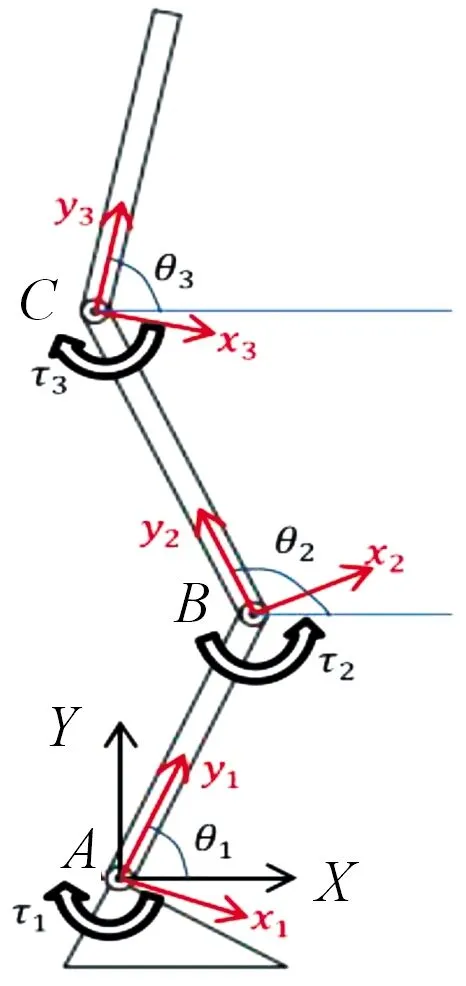
圖1 人體三連桿剛體模型示意圖

設小腿、大腿和軀干的長度分別為l1、l2和l3，關節回轉中心分別為A、B、C，對于踝關節角度θ1，膝關節中心B在坐標系{o1x1y1z1}下的位置矢量為：

(1)

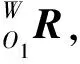
(2)

則膝關節中心B在坐標系{OXYZ}下的位置矢量為：

(3)

A點到B點的方向向量記為a，故a為：

(4)

因此，向量a與X軸正方向的夾角即踝關節角度為：

(5)

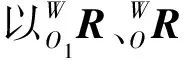
(6)

因此：

θ1=cos-1(ox)

(7)

同理，θ2、θ3可由同樣的方法得到。

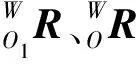
該姿態傳感器在用歐拉角表示姿態時的坐標系旋轉順序為z-y-x，這種描述姿態傳感器上的局部坐標系{oixiyizi}的方位的法則為：局部坐標系{oixiyizi}的初始方位與慣性坐標系W相同，首先使其繞zi軸旋轉γ角，然后繞yi軸旋轉β角，最后繞xi軸旋轉α角，其中各次旋轉都是相對于運動坐標系的某軸進行的，從而得到表達式：

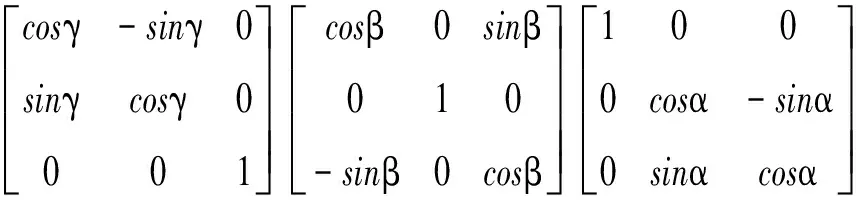
(8)

即旋轉變換通式：

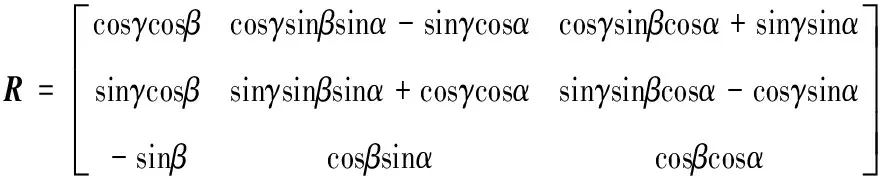
(9)

1.2 坐站轉移的動力學建模

剛體動力學分析的主要方法有牛頓—歐拉方法、拉格朗日方法，牛頓—歐拉方法在運用時既要考慮外界驅動力，又要考慮產生加速度的慣性力，拉格朗日方法則基于系統能量的概念，這種方法只需速度而不必求各桿件的內作用力，直接求出關節的驅動力矩，是一種比較清晰簡便的方法[20]。本研究采用拉格朗日方法進行動力學分析。

在任一時刻，連桿1的質心位置：

xc1=lc1cosθ1

(10)

yc1=lc1sinθ1

(11)

連桿2的質心位置：

xc2=l1cosθ1+lc2cosθ2

(12)

yc2=l1sinθ1+lc2sinθ2

(13)

連桿3的質心位置：

xc3=l1cosθ1+l2cosθ2+lc3cosθ3

(14)

yc3=l1sinθ1+l2sinθ2+lc3sinθ3

(15)

其中：lci(i=1，2，3)為體段i質心到其局部坐標系原點的距離。

在坐站轉移過程中，當人體脫離座位后，此時只受到地面對人體的作用力，所以此時系統的勢能為：

m1glc1sinθ1+m2g(l1sinθ1+lc2sinθ1)+

m3g(l1sinθ1+l2sinθ2+lc3sinθ3)

(16)

其中：mi表示剛體i的質量，g表示重力加速度。

系統的動能為：

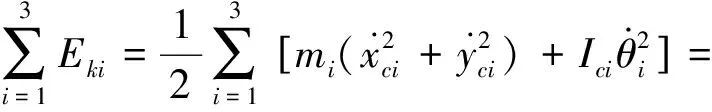
(17)

其中：Ici(i=1，2，3)表示剛體i相對于其質心的質量慣性矩。

拉格朗日函數L定義為系統的動能Ek與總勢能Ep之差，即：

(18)

則系統的動力學方程為：

(19)

聯立可得，脫離座位后各關節力矩：

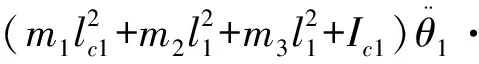
(m1lc1+m2l1+m3l1)gcosθ1

(20)

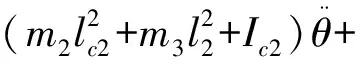
(m2lc2+m3l2)gcosθ2

(21)

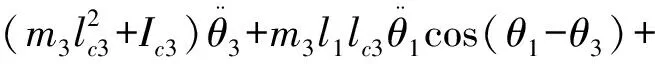
(22)

在坐站轉移運動中，由于軀干所受的外力始終只有重力作用，在脫離座位前，式(22)仍然適用。

由牛頓第二定律可知，地面的支撐反力為：

Fy=(m0+m1+m2+m3)g+

(23)

2 實驗及結果分析

2.1 實驗

為驗證前述方法的準確性與可行性，搭建了基于姿態傳感器的人體坐站轉移運動測量系統，通過3個姿態傳感器采集人體坐站轉移過程中的下肢關節角度信息。同時，利用測力踏板采集人體坐站轉移運動過程中足部受到的地面反力，如圖2所示。

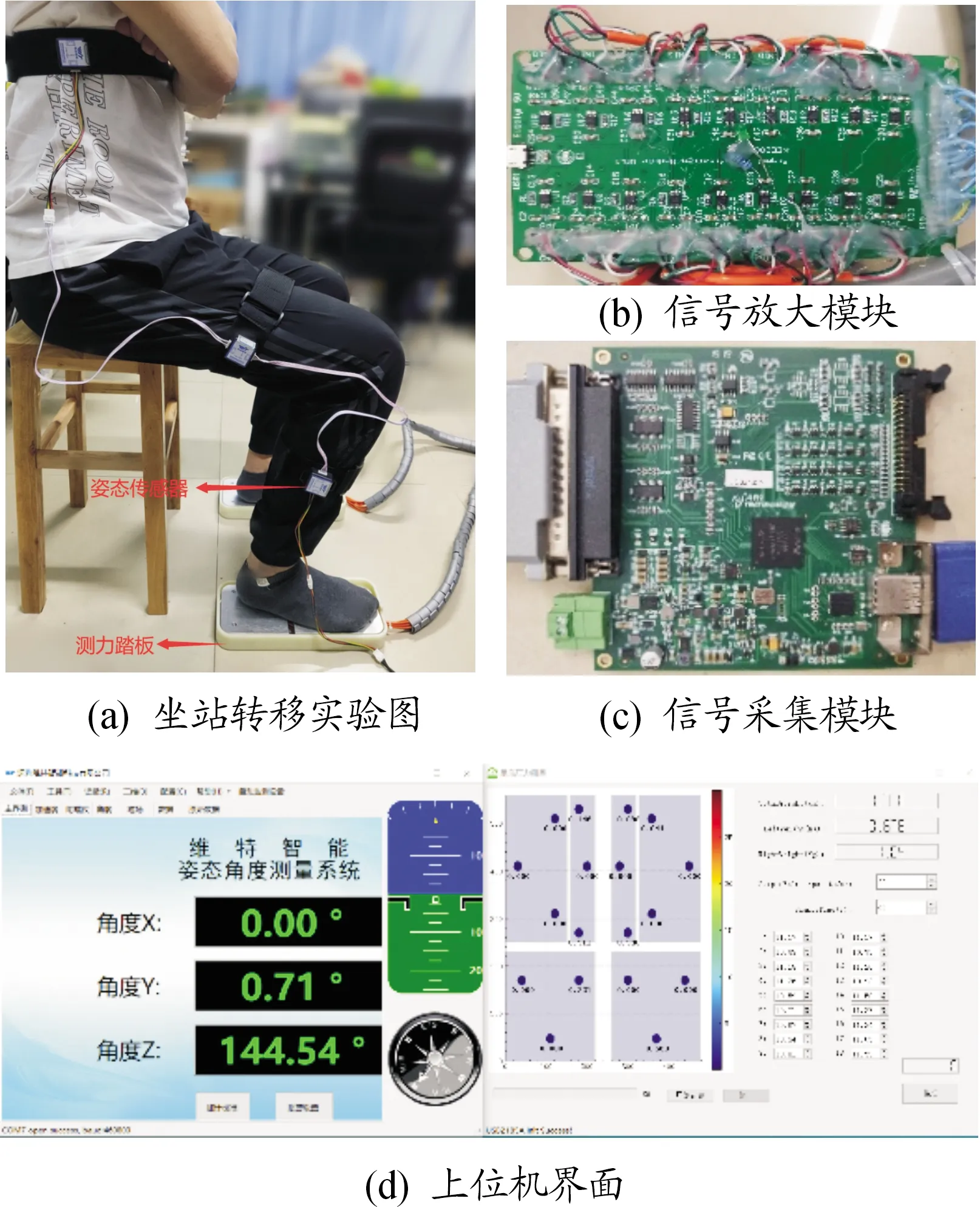
圖2 坐站轉移運動測量系統

采用深圳維特智能科技有限公司型號為WT 901C 485的姿態傳感器，該傳感器支持多個模塊級聯，在上位機上能夠同時采集多個模塊的數據，該模塊內部集成了高精度的陀螺儀、加速度計、地磁場傳感器，能夠在動態環境下準確輸出模塊的當前姿態，姿態測量精度0.01°，加速度測量精度0.01g，角速度測量精度0.05(°)/s；姿態傳感器通過USB直接與上位機通信，采樣頻率為50 Hz；測力踏板壓力傳感器選用蚌埠大洋傳感公司型號為DYLY-108的壓力傳感器，量程為50 kg；該傳感器的輸出靈敏度為1.0～2.0 mV/V，工作電壓為5.0～10.0 V；測力踏板通過信號放大模塊和信號采集模塊與上位機實時通信，采樣頻率為50 Hz。

實驗招募了7名健康且沒有任何運動障礙的男性在校學生，7名受測者的基本信息如表1所示。根據《GB/T 1000—1988.中國成年人人體尺寸》和《GB/T 17245—2004.成年人人體慣性參數》，受測者的各項人體測量學數據如表2所示。表2中給出了7名受測者各肢段的長度li、質量mi、質心位置lci以及關于質心的轉動慣量Ici，在實驗中，受測者以平時的習慣性坐姿為準，雙手自然放置于膝蓋上，座位高約為0.45 m，3個姿態傳感器通過綁帶分別固定于小腿、大腿、軀干位置，保證每個姿態傳感器的y軸方向沿著所在肢段兩端關節的連線，并由下端指向上端，2個測力踏板放置于受測者腳下，左右距離以個人平時習慣性坐姿為準，由于健康人群的坐站轉移運動通常被認為是關于矢狀面對稱的[18]，因此在實驗中只采集身體一側的運動數據；受測者穿戴好實驗器材后，要求受試者保持穩定的站立姿勢，對姿態傳感器的安裝誤差進行校準；由于實驗對象都是健康的大學生群體，因此本研究認為，在靜態站立時，受測者身體與地面保持垂直，以此校準姿態傳感器的安裝誤差。

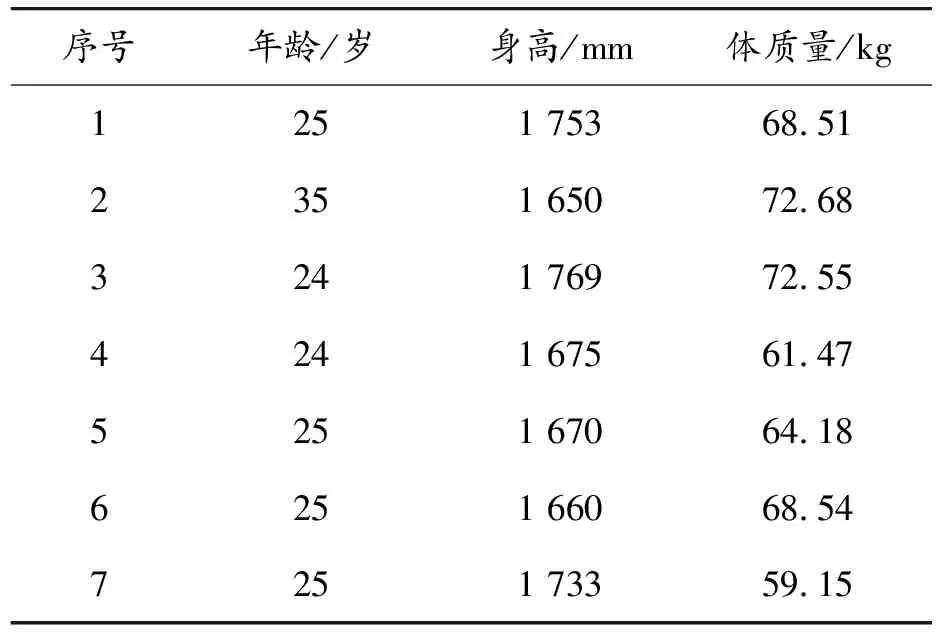
表1 7名受測者的基本信息

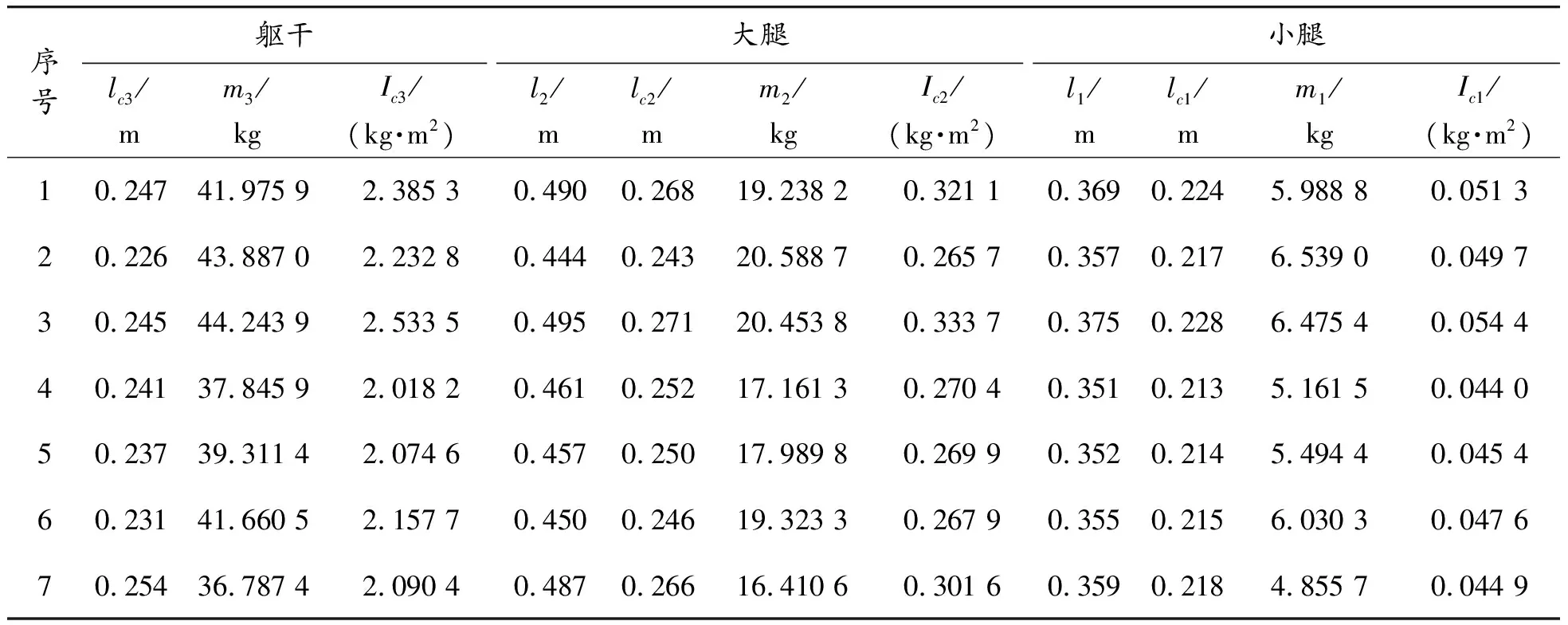
表2 7名受測者的人體測量學數據

2.2 實驗結果分析

實驗完成后，將受測者的坐站轉移時間做歸一化處理，將足底壓力與受測者體重進行標準化處理；最終得到7名受測者坐站轉移運動的關節角度數據和足底壓力數據；其中1名受測者的坐站轉移運動的關節角度曲線和足底壓力曲線如圖3、4所示，圖中A1、B1、C1分別表示θ1、θ2、θ3在運動初始時刻的角度；A2、C2分別表示θ1、θ3在運動過程中的最大屈曲角度；A3、B3、C3分別表示θ1、θ2、θ3在運動結束時刻的角度(最大伸展角度)，同理，F1、F2、F3、F4、F5分別表示運動初始時刻的壓力值、運動過程中的壓力峰值以及運動終止時刻的壓力值；7名受測者各個時刻的角度數據和足底壓力數據見表3、4。

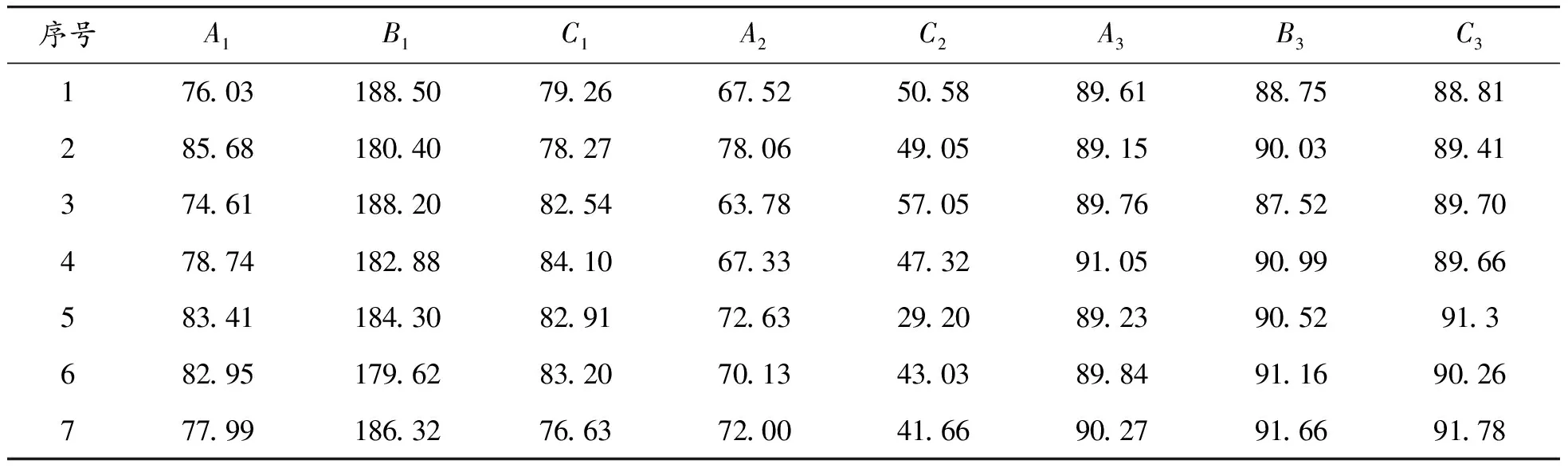
表3 7名受測者各時刻關節角度數據 (°)

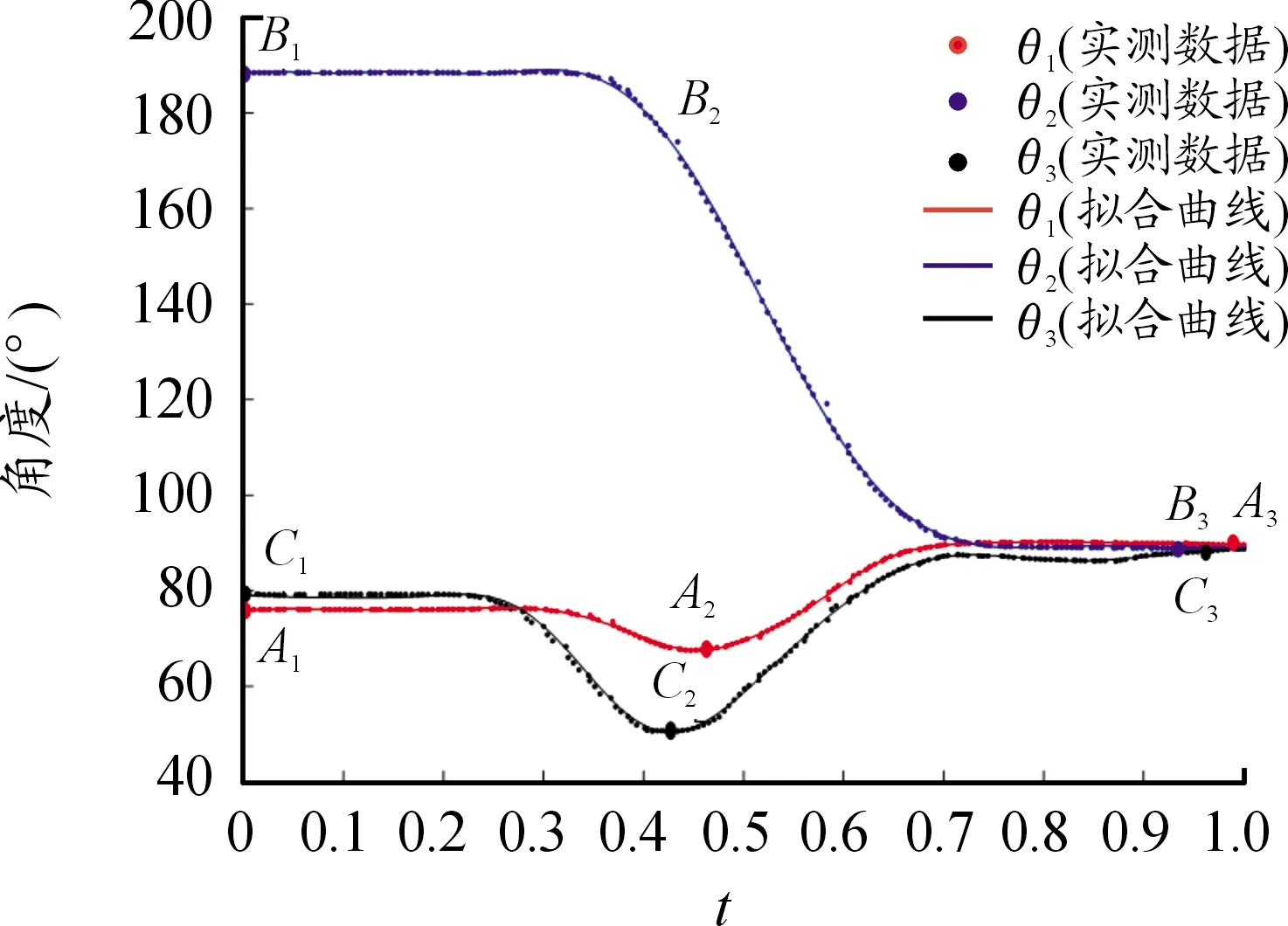
圖3 1名受測者坐站轉移的關節角度曲線

由圖3、4可知，在坐站轉移的開始階段，此時軀干與水平面夾角大約為80°，之后髖關節角度開始變化，軀干開始前傾，此時足底壓力開始減小，當足底壓力到達第一個波谷后(F2)，踝關節和膝關節開始運動，身體由一個穩定的坐姿狀態加速上升，此時足底壓力快速增大，當足底壓力達到最大值后(F3)，重心繼續上升，足底壓力開始減小，當足底壓力到達第二個波谷后(F4)，足底壓力開始增大，身體逐漸伸直至完全站立。

為了驗證姿態角解算關節角度的正確性，將關節角度數據代入式(23)，從而得出足底壓力的理論計算數據，由于姿態傳感器放置在衣服的外側，人體肌肉的形變和衣服的滑移，使姿態傳感器相對于非剛性的人體產生微小的位姿變化，造成曲線的不圓滑，本研究對角度曲線進行了擬合，如圖3所示。將擬合后的關節角度曲線數據代入式(23)，進而得出足底反力的理論計算數據；在坐站轉移過程中，當人體離開座位前，式(23)的計算數據不能反映足底的受力情況，因此需要確定人體離開座位的時間點。文獻[21]中，當足底的支撐反力達到最大時，認為可作為離開座位的時刻。本文中以最大地面反力出現的時刻(F3)為起始點，將實際測量的地面反力數據與理論計算結果進行對比，其中1名受測者理論計算數據和實際測量數據曲線見圖4，7名受測者數據見表5。表5中給出了離開座位后，足底壓力的理論計算與實測數據間的均方根誤差(RMSE)和相關系數(R)。從表5可以看到，通過理論計算和測力板得到的地面反力二者間具有較大的相關系數(R≥0.91)，實測數據和理論計算數據有一定的誤差，但誤差較小(RMSE≤0.44)；因此，基于姿態傳感器的測量系統是可靠的，可以用于坐站轉移的研究。通過分析左右測力踏板各自壓力數據可以發現，在坐站轉移過程中，左右腳的足底壓力并不是對稱的，如圖5所示，因此，足底壓力的不對稱性在一定程度上反映了運動的不對稱性，使理論計算數據與實際測量數據之間存在偏差，然而從實驗結果來看，這種運動不對稱性對于誤差的影響并不大，在實際應用中，對于偏癱和下肢功能障礙者，可能需要同時采集左右兩側的關節角度數據；另外，本研究力學模型的參數是根據受測者的體重和身高按照國家標準提供的回歸方程求得，與實際人體的質量分布和體段參數存在較大差異，這也造成了誤差。

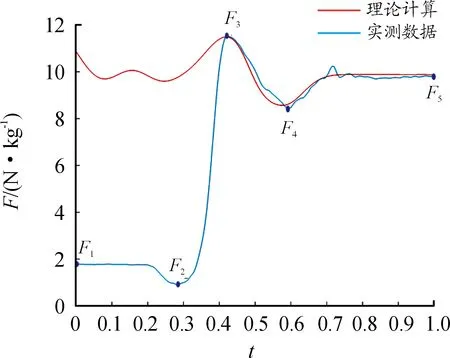
圖4 1名受測者坐站轉移的足底壓力曲線

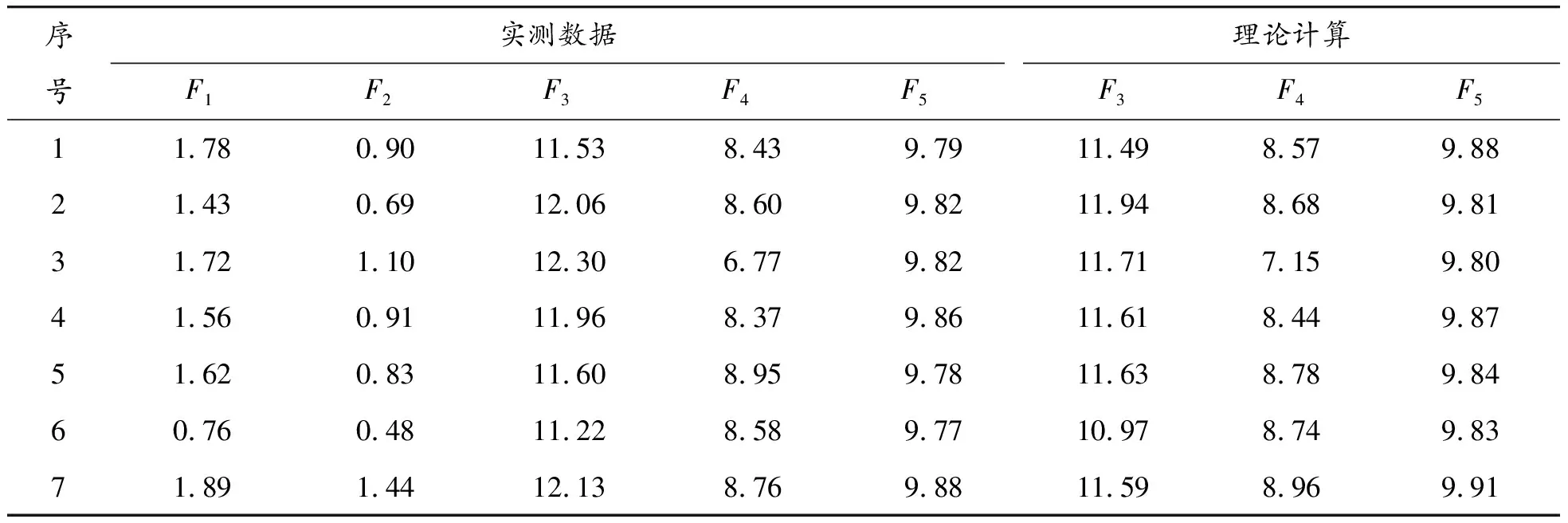
表4 7名受測者各時刻足底壓力數據 N/kg

表5 7名受測者足底壓力的理論計算與實測數據

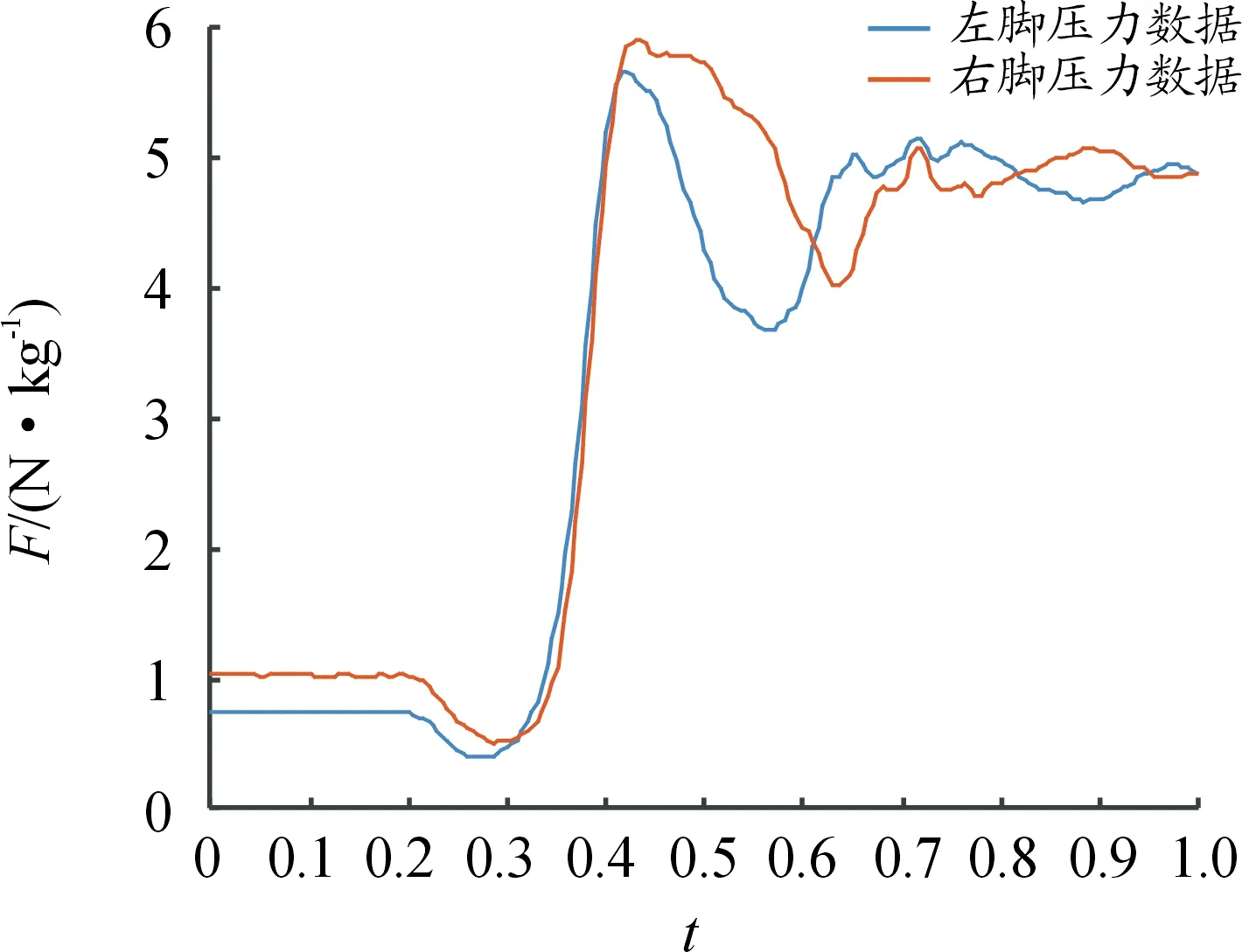
圖5 1名受測者坐站轉移的左、右腳足底壓力曲線

在坐站轉移運動中，關節峰值力矩是評估其下肢能力的重要指標[10]，因此，將姿態傳感器測得的關節角度數據代入式(20)～(22)中，根據表2中的人體各項體段參數，得到坐站轉移過程中髖關節、膝關節和踝關節的力矩曲線，如圖6所示。當人體離開座位前，由于沒有考慮人體與座位之間的接觸力，因此只繪出離開座位之后的膝關節和踝關節力矩曲線(逆時針方向為正)，圖中虛線表示離開座位的時刻；每個關節的力矩與身體質量乘以身高進行歸一化，以便于不同體型受試者之間的比較。由圖6可知，在坐站轉移的開始階段，髖關節力矩小于0.1 N·m/(kg·m)，在軀干前傾階段，髖關節力矩逐漸增大，在離開座位后很短一段時間內，髖關節力矩達到最大值，之后髖關節、膝關節和踝關節力矩逐漸減小，軀干、大腿和小腿逐漸伸直。7名受測者的關節最大峰值力矩見表5所列，在坐站轉移實驗中，7名受測者膝關節力矩峰值均大于1.0 N·m/(kg·m)，其中有6名受測者的膝關節力矩峰值大于1.2 N·m/(kg·m)，這是因為在坐站轉移運動中，膝關節需要通過較大的角位移來使身體重心向上運動，這也意味著膝關節損傷患者在進行坐站轉移運動時可能更容易跌倒。在7名受測者中，受測者1和受測者3的踝關節峰值力矩大于其髖關節峰值力矩，由表1可知，受測者1和受測者3的身高較其他受測者更高，這可能意味著更高的身高需要更大的踝關節力矩控制身體重心位于足底支撐面內。

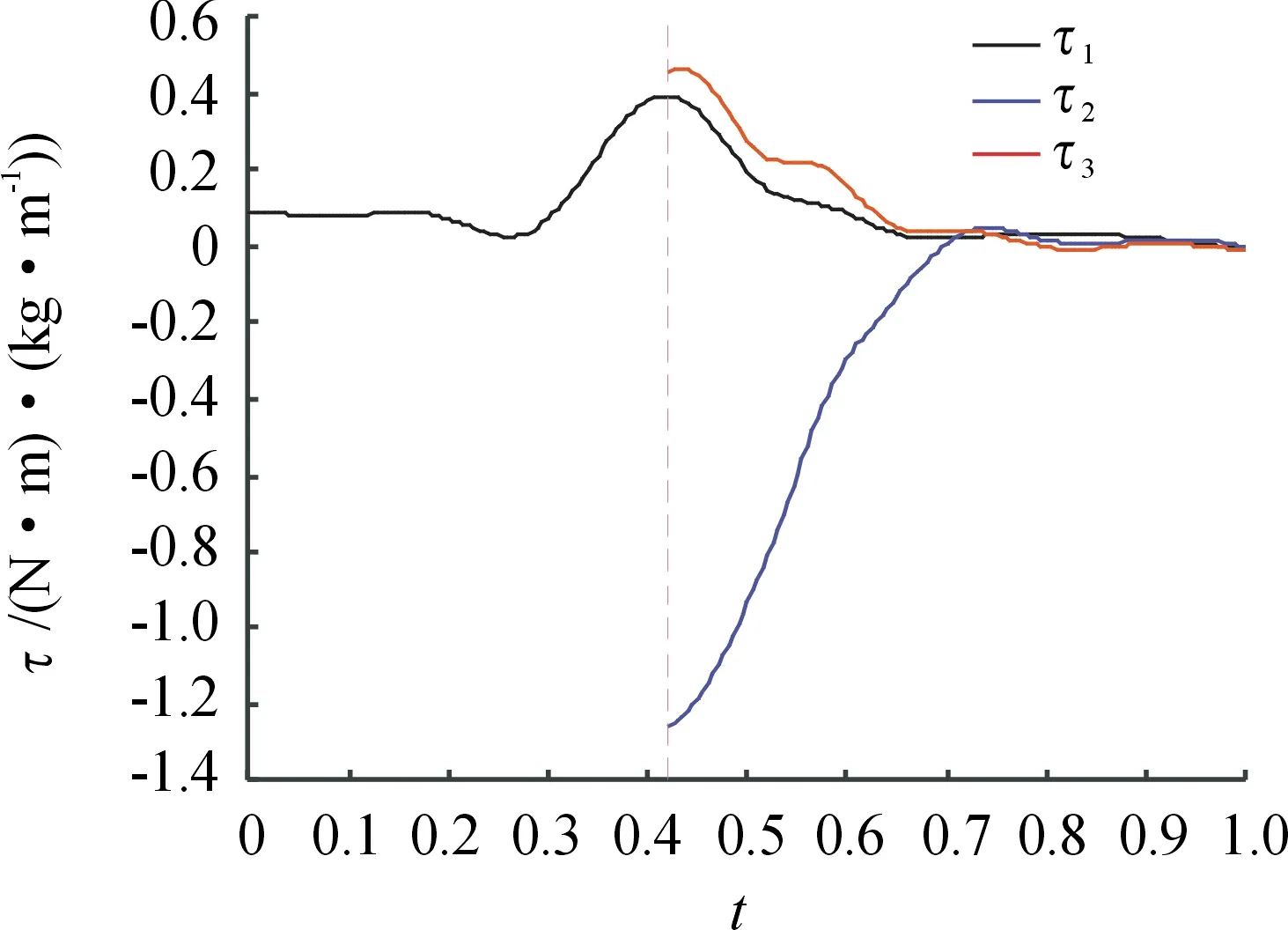
圖6 1名受測者坐站轉移的關節力矩曲線

表6 7名受測者的關節最大峰值力矩 N·m/(kg·m)

3 結論

搭建了一種基于姿態傳感器的人體坐站轉移運動測量系統，通過姿態傳感器采集的姿態角解算人體坐站轉移的下肢關節角度數據，利用足底測力踏板驗證了基于姿態傳感器的測量系統的可行性與有效性，實測地面反力數據與理論計算地面反力數據相關系數R≥0.91，均方根誤差RMSE≤0.44，通過拉格朗日動力學方法計算了人體坐站轉移過程中關節的最大峰值力矩，其中踝關節平均最大峰值力矩為(0.413±0.091)N·m/(kg·m)，膝關節絕對平均最大峰值力矩為(1.241±0.076)N·m/(kg·m)，髖關節最大峰值力矩為0.427±0.065 N·m/(kg·m)。

由于本研究的實驗對象僅限于7名健康大學生，其運動學和動力學參數不足以涵蓋所有人群，為了進一步提高基于姿態傳感器的人體坐站轉移測量系統的準確性，應對不同的群體開展更廣泛的研究，以驗證該系統的穩定性和可靠性。同時，應對坐站轉移過程中下肢對稱進一步研究，對于偏癱及對于坐站轉移障礙患者的平衡評估具有重要意義。

基于姿態傳感器的人體坐站轉移測量系統，相較于運動捕捉系統，更能滿足臨床的實際應用，為坐站轉移康復評估提供了更加便利的方法，也可以為坐站康復訓練器具的研發提供參考。