異質(zhì)信息網(wǎng)絡(luò)中基于網(wǎng)絡(luò)嵌入的影響力最大化

楊宇迪，周麗華,2，杜國王，鄒星竹，丁海燕

（1.云南大學 信息學院，云南 昆明 650504;2.云南大學 滇池學院，云南 昆明 650228）

影響力最大化問題是指在特定的擴散模型下，尋找一組初始擴散節(jié)點使影響擴散范圍最大的優(yōu)化問題。目前，影響力最大化算法主要分為兩類：貪心算法[1-3]和啟發(fā)式算法[4-6]，其中貪心算法主要用于提高算法的精確度；啟發(fā)式算法主要用于解決實際問題以提高算法效率。Kempe 等[7]首次形式化定義了影響力最大化問題，并提出了一個貪心算法，其近似值約為 1?/e?ε，但是該算法的效率較低。Leskovec 等[8]提出了CELF 算法，Goyal 等[9]提出了CELF++算法，通過實驗發(fā)現(xiàn)該算法比CELF 快35%～55%。接著，為了解決貪心算法的效率問題，Tang 等[10]提出一種基于跳的算法，該算法可以在常用的擴散模型(獨立級聯(lián)模型和線性閾值模型)下輕松應(yīng)用于十億規(guī)模的網(wǎng)絡(luò)。Peng 等[11]認為個體之間的影響有直接影響和間接影響，社會影響力的強弱取決于個體之間的關(guān)系、網(wǎng)絡(luò)距離、時間、網(wǎng)絡(luò)和個體的復雜性和不確定性。但這些算法通常僅將社會網(wǎng)絡(luò)看作同質(zhì)網(wǎng)絡(luò)，忽略了社會網(wǎng)絡(luò)的異質(zhì)性，即網(wǎng)絡(luò)中包含不同類型的對象和鏈接。在異質(zhì)信息網(wǎng)絡(luò)(heterogeneous information network，HIN)中，影響力可以通過不同的對象和鏈接進行擴散，從而獲得更廣泛的影響范圍。

盡管異質(zhì)信息網(wǎng)絡(luò)豐富的結(jié)構(gòu)和語義信息有助于實現(xiàn)影響力擴散范圍最大化，但也給影響力的分析帶來了挑戰(zhàn)。目前，HIN 中的數(shù)據(jù)挖掘任務(wù)主要集中于相似性搜索[12-13]、聚類[14-15]、分類[16-17]等，很少有研究者關(guān)注HIN 中的社會影響力分析。為了建模HIN 中的社會影響力，Yang 等[18]提出了一種基于元路徑的信息熵模型MPIE，利用多條元路徑從異質(zhì)信息網(wǎng)絡(luò)中提取多個同質(zhì)信息網(wǎng)絡(luò)，在每個同質(zhì)信息網(wǎng)絡(luò)中基于熵度量直接影響力和間接影響力，然后融合多個同質(zhì)信息網(wǎng)絡(luò)中的影響力度量HIN 中的社會影響力。盡管MPIE 取得了一定的效果，但該算法需選擇特定類型的節(jié)點設(shè)定元路徑，不能靈活地度量HIN 中不同類型節(jié)點間的影響。

HIN 嵌入[19-21]旨在通過基于節(jié)點的結(jié)構(gòu)特性保留不同類型節(jié)點之間的鄰近性來學習各個不同類型的節(jié)點的低維表示，而這些低維表示可直接應(yīng)用于網(wǎng)絡(luò)分析任務(wù)，比如節(jié)點分類、聚類以及鏈路預測等。由于HIN 嵌入將不同類型節(jié)點映射于同一向量空間，用同一空間的低維向量來描述不同類型的節(jié)點，不僅概括了網(wǎng)絡(luò)的重要結(jié)構(gòu)特征，而且學習到的嵌入具有同質(zhì)性，易于使用和集成。最近幾年，異質(zhì)信息網(wǎng)絡(luò)的表征學習受到了研究者的廣泛關(guān)注。

因此，本文提出了一種異質(zhì)網(wǎng)絡(luò)中基于網(wǎng)絡(luò)嵌入的影響力最大化模型IMNE。IMNE 首先利用網(wǎng)絡(luò)嵌入學習HIN 中所有節(jié)點在同一向量空間的低維表征，保持不同類型節(jié)點在同一度量空間，然后基于HIN 原始的網(wǎng)絡(luò)拓撲結(jié)構(gòu)，擴展傳統(tǒng)的信息熵模型，考慮多種影響因素，度量HIN 中不同類型節(jié)點的社會影響力并選擇最具影響力的節(jié)點作為初始擴散節(jié)點，最后，選擇特定的信息擴散模型實現(xiàn)HIN 中的影響力最大化。本文工作一方面擴展了HIN 嵌入的應(yīng)用，另一方面將Peng 等[1]所提的模型擴展到了HIN。

1 相關(guān)符號和問題定義

定義1 異質(zhì)信息網(wǎng)絡(luò)[22]。異質(zhì)信息網(wǎng)絡(luò)通常被定義為一個帶有對象類型映射函數(shù)?:V→A和邊類型映射函數(shù)φ:E→R的無向圖G=(V,E)，其中每個對象v∈V屬于一個特定的對象類型?(v)∈A，每條邊e∈E屬于一個特定的關(guān)系類型φ(e)∈R，且 |A|+|R|>2。

定義2 HIN 中的影響力最大化。給定一個異質(zhì)信息網(wǎng)絡(luò)G={V,E}，δ(Vs)是將種子集Vs映射到受種子集影響的對象數(shù)量的影響函數(shù)，異質(zhì)信息網(wǎng)絡(luò)中影響力最大化的目的是選擇一組最具影響力的種子集且該種子集可以最大化影響力的擴散范圍，即

2 IMNE 模型

本節(jié)將詳細介紹異質(zhì)網(wǎng)絡(luò)中基于網(wǎng)絡(luò)嵌入的影響力最大化模型IMNE。

首先以圖1 為例說明本文動機。如果將學術(shù)網(wǎng)絡(luò)視為同質(zhì)網(wǎng)絡(luò)，該網(wǎng)絡(luò)中僅Lily 和Bob、Ada 和Tom 間存在邊，此時，若將Ada 作為初始擴散節(jié)點，其將僅影響Tom 一個節(jié)點，即影響范圍為1。然而，若將學術(shù)網(wǎng)絡(luò)視為HIN，如圖2 所示，該網(wǎng)絡(luò)中包含3 種類型的節(jié)點，論文和會議之間存在發(fā)表/被發(fā)表關(guān)系，論文和論文之間存在引用/被引用關(guān)系，作者和論文之間存在撰寫/被撰寫關(guān)系，考慮不同類型節(jié)點通過不同關(guān)系互相影響，令Ada 作為初始擴散節(jié)點，則P2 和P6 兩篇論文會受到Ada 的直接影響，其次，由于Ada 和Tom 之間通過路徑“Tom-P2-Ada(合作)”相關(guān)聯(lián)，Ada 和Mary 通過“Ada-P6-C1-P5-Mary(共同參加會議)”相關(guān)聯(lián)，所以Ada 也可間接影響Tom 和Mary。相比同質(zhì)網(wǎng)絡(luò)，Ada 的影響范圍更廣。

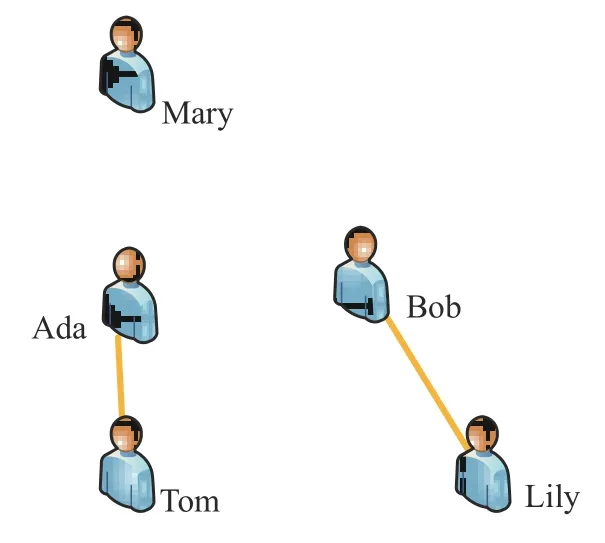
圖1 同質(zhì)網(wǎng)絡(luò)示例Fig.1 Example of a homogeneous network

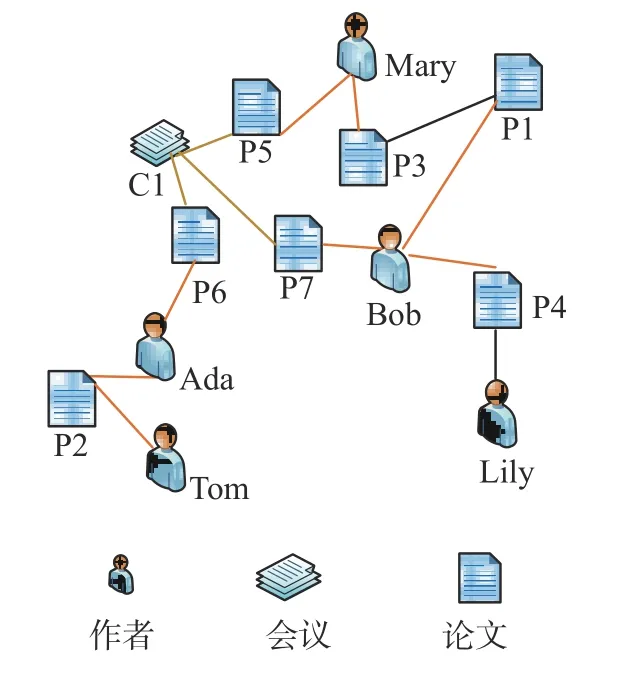
圖2 異質(zhì)網(wǎng)絡(luò)示例Fig.2 Example of a HIN

IMNE 模型的整體框架如圖3 所示。首先，IMNE 從HIN(圖3(a))中學習各種類型節(jié)點的嵌入(圖3(b))，然后，擴展信息熵模型度量社會影響力，并選取最具影響力的節(jié)點作為種子集(圖3(c))；最后在特定擴散模型下實現(xiàn)影響力最大化(圖3(d))。

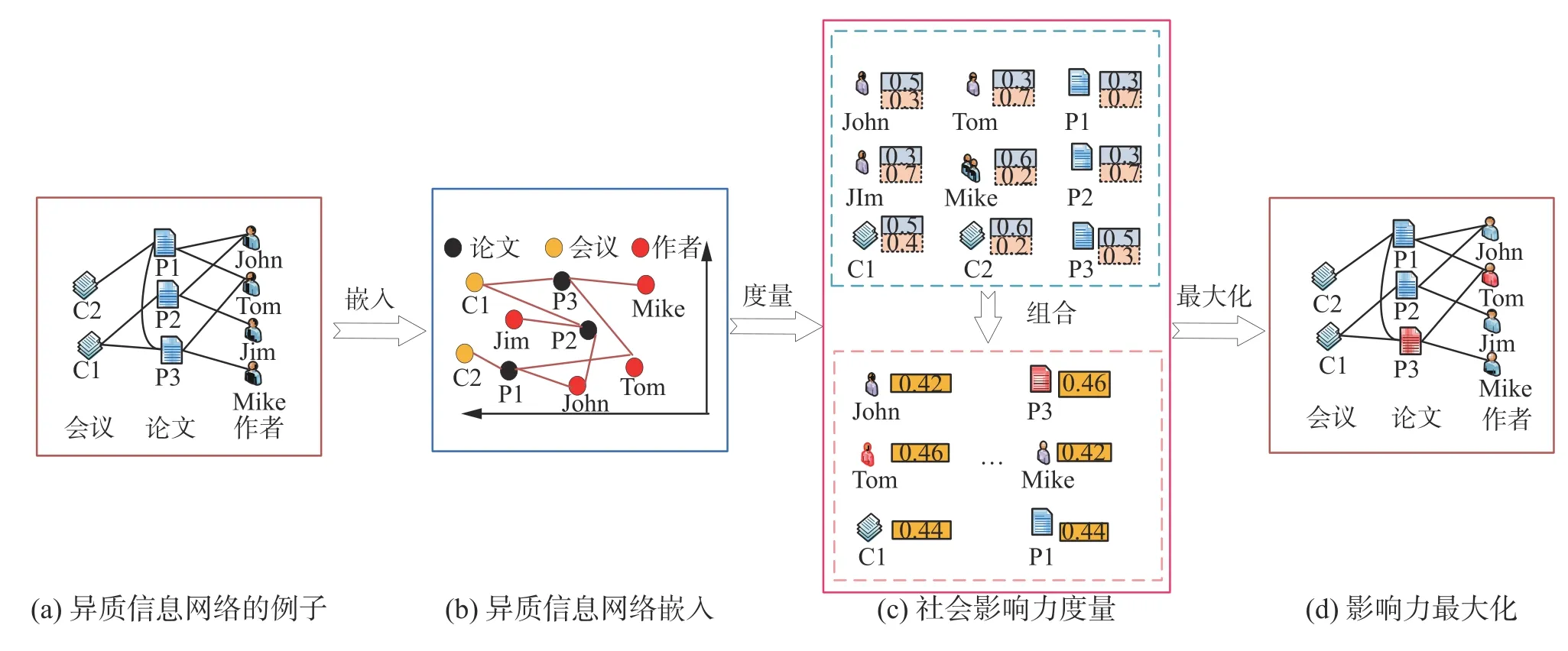
圖3 IMNE 模型的具體框架Fig.3 The specific framework of the IMNE model

2.1 HIN 嵌入

本文使用HIN2Vec 模型[23]實現(xiàn)HIN 嵌入。HIN2Vec 模型旨在通過最大程度地聯(lián)合預測節(jié)點之間關(guān)系的可能性來學習節(jié)點向量和關(guān)系向量。模型采用一對節(jié)點x和y，以及某種關(guān)系r∈R的one-hot 向量x、y和r作為輸入，通過神經(jīng)網(wǎng)絡(luò)將x、y和r轉(zhuǎn)化為隱藏層中的潛向量中關(guān)系和節(jié)點的語義含義不同，所以關(guān)系向量r通過正則化轉(zhuǎn)化為限制r的值在0 到1 之間)，在輸出層通過Sigmoid實現(xiàn)邏輯分類(⊙ 表示逐元素相乘)。通過HIN2Vec，HIN 中的每個節(jié)點轉(zhuǎn)換為同一向量空間的低維度潛在表示，在捕獲和表示HIN 中的豐富信息的同時，有效避免了HIN 中不同類型節(jié)點和關(guān)系的不兼容性，便于度量不同類型節(jié)點的社會影響力以選取初始擴散種子集。

2.2 影響力度量

HIN 中，一個對象的社會影響力通常不僅體現(xiàn)于緊密的直接聯(lián)系，還體現(xiàn)在節(jié)點的間接聯(lián)系。HIN 中社會影響的相關(guān)定義如下：

定義3 直接/間接影響力。給定異質(zhì)信息網(wǎng)絡(luò)G中的對象u、v，若對象u和v之間有邊相連，即euv=1，則Deu(v)表示對象u和對象v間的直接影響力；若對象u和v之間沒有邊直接相連，即euv=0，則IIu(v)表示對象u和對象v間的間接影響力。

定義4 全局影響力。給定異質(zhì)信息網(wǎng)絡(luò)G中的節(jié)點u，若節(jié)點u在整個網(wǎng)絡(luò)中具有影響力，那么Iu被定義為節(jié)點u在G上的全局影響力。

全局影響力與直接/間接影響力有著密切關(guān)系。如果對象具有很強的直接和間接影響力，則該對象通常在社會網(wǎng)絡(luò)中具有較強的全局影響力。IMNE 算法考慮了不同類型對象之間的影響(如作者對論文的影響或論文對作者的影響)，通常具有影響力的對象其相關(guān)行為也具有影響力。例如，在數(shù)據(jù)挖掘領(lǐng)域具有較強影響力的研究人員，他發(fā)表的論文在數(shù)據(jù)挖掘領(lǐng)域通常也具有較高的影響力。

2.2.1 直接影響力度量

在社交網(wǎng)絡(luò)中，影響力與許多潛在因素相互作用，如相似性和相關(guān)性，相似對象之間的相互影響往往更強，例如，在學術(shù)網(wǎng)絡(luò)中，作者i與作者j、作者m均有合作，若作者i與作者j的研究領(lǐng)域更相似，那么作者i和j間的相互影響往往更強。同時，度中心性作為圖論中度量節(jié)點相對重要性的評價指標，也是社會影響力的潛在影響因素。

根據(jù)HIN 嵌入得到的各類型節(jié)點的嵌入信息，可獲得HIN 中各類型節(jié)點的相似度 Simij，即：

式中：ei和ej分別對應(yīng)對象i和j的潛在表征向量；(·) 表示向量的點積；∥e∥ 表示向量的長度。

HIN 網(wǎng)絡(luò)嵌入不僅將不同類型節(jié)點映射于同一空間便于度量不同類型節(jié)點間的社會影響，還保留HIN 原始結(jié)構(gòu)，故給定異質(zhì)信息網(wǎng)絡(luò)G，令Ni表示對象i的度，對象i的直接影響力的定義如下：

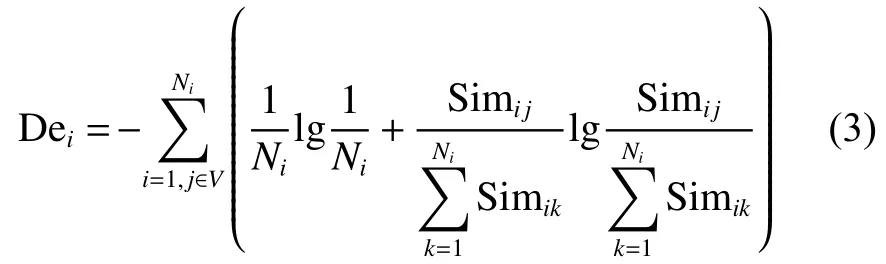
其中i≠j且i≠k。

2.2.2 間接影響力度量

除了直接影響力，對象之間往往也具有某種間接影響，例如，在學術(shù)網(wǎng)絡(luò)中，具有影響力的作者可以通過論文或會議影響其他作者。

給定異質(zhì)信息網(wǎng)絡(luò)G，令Nik表示對象i和k間公共對象的數(shù)量，則對象i和k之間的間接影響力描述如下：

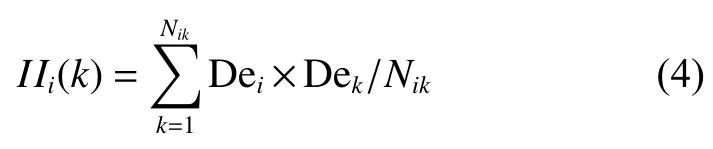
令Mi表示對象i的多跳連接對象的數(shù)量，對象i的間接影響力IIi的定義如式(5)所示。

2.2.3 全局影響力度量

根據(jù)直接影響力和間接影響力的度量可得，對象i的全局影響力如式(6)所示。

式中：α和 β分別表示直接影響力 Dei和間接影響力IIi的權(quán)重，且 α+β=1。

2.3 IMNE 算法描述

算法1 IMNE 算法

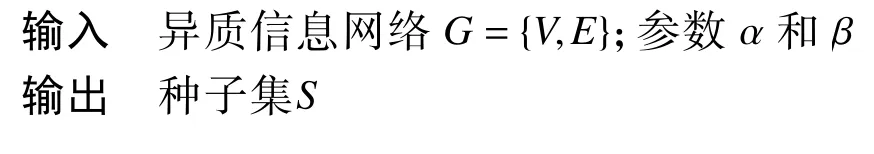
該算法中語句3～11 用以選擇最具影響力的k個對象作為種子節(jié)點集S。IMNE 算法的復雜度為O(m+nd+nlog(k))，其中n表示異質(zhì)信息網(wǎng)絡(luò)中對象的數(shù)量，n=|V|；k表示最具影響力的對象數(shù)量；d表示一跳鏈接對象的平均數(shù)量；m表示異質(zhì)信息網(wǎng)絡(luò)中邊的總數(shù)，m=|E|。

3 實驗評估

3.1 實驗準備

3.1.1 數(shù)據(jù)集

本文實驗部分共使用了3 個真實的HIN 數(shù)據(jù)集，來自兩種不同領(lǐng)域，其中4-area 數(shù)據(jù)集來自學術(shù)領(lǐng)域，Yelp 數(shù)據(jù)集和Amazon 數(shù)據(jù)集來自商業(yè)領(lǐng)域。4-area[24]是從DBLP 網(wǎng)站收集的子數(shù)據(jù)集，涉及數(shù)據(jù)庫、數(shù)據(jù)挖掘、機器學習和信息檢索4 個研究領(lǐng)域，共包含20 場會議、排名前5 000的作者、14 328 篇論文和8 789 個術(shù)語，其中作者與論文、論文與會議、論文與術(shù)語之間存在聯(lián)系。Yelp 數(shù)據(jù)集記錄了1 268 條用戶對坐落于47 個城市、3 種類型的2 614 條商戶的評分情況，其中用戶與商戶、商戶與城市、商戶與類型之間存在聯(lián)系。Amazon 是一種商業(yè)網(wǎng)絡(luò)，該網(wǎng)絡(luò)記錄了6 170 個用戶對來自334 個品牌旗下的22 種類別共2 753 項產(chǎn)品的3 857 條評論情況，其中用戶與產(chǎn)品、產(chǎn)品與評論、產(chǎn)品與類別、產(chǎn)品與品牌之間存在聯(lián)系。以上3 個數(shù)據(jù)集，除了來自不同的領(lǐng)域，還具有不同的稀疏性，其中Yelp 的數(shù)據(jù)分布最稀疏，Amazon 數(shù)據(jù)分布最密集。在實驗過程中選擇HIN2Vec[13]模型嵌入HIN 數(shù)據(jù)集，使不同類型節(jié)點處于同一度量空間。

3.1.2 擴散模型

影響力最大化旨在正確識別一組種子集以使它們在特定擴散模型下影響力的擴散范圍最大化。本文選擇SIR 模型[25]和線性閾值模型共兩種模型作為擴散模型，在SIR 模型實驗中，感染概率 γ 設(shè)為0.8，恢復概率 θ 設(shè)為0.5，種子集大小設(shè)為1～100；在線性閾值模型實驗中，其閾值設(shè)置為0.5，種子集大小設(shè)為0～50。

3.1.3 對比算法

采用DC、PageRank、Entropy-based、MPIE 和IMNE-D 算法作為對比算法，驗證IMNE 算法實現(xiàn)HIN 中影響力最大化的有效性。其中DC、PageRank 算法是常見的影響力最大化中選擇種子集的方法；Entropy-based 算法[11]是同質(zhì)網(wǎng)絡(luò)中不僅考慮直接影響和間接影響，還考慮影響力擴散的一種方法，有助于對比異質(zhì)信息對種子集選擇的影響；其次，IMNE 算法除了實現(xiàn)HIN 中的影響力最大化，還可以度量HIN 中節(jié)點的社會影響力，而MPIE 算法是基于元路徑度量HIN 中節(jié)點影響力的方法，因此，本文還選擇MPIE 算法[18]作為對比算法，分析IMNE 算法在HIN 中度量節(jié)點社會影響力的效果。

在實驗中，DC、PageRank 和Entropy-based 方法將忽略HIN 中節(jié)點和鏈接的異質(zhì)性，直接在整個網(wǎng)絡(luò)(4-area、Yelp 和Amazon)上運行，實驗結(jié)果包含各種不同類型的節(jié)點。IMNE-D 是IMNE 算法的變體，主要通過計算節(jié)點的直接影響力來選擇種子集，未考慮非直接相連的節(jié)點間的影響，有助于對比間接影響力對影響力最大化的作用。特別地，基準算法中的參數(shù)均選擇實驗結(jié)果最優(yōu)參數(shù)。

3.1.4 評估指標

1) 在SIR 模型實驗中，將感染率(Infection rate)和感染時間(Infection time)作為評估指標驗證IMNE 算法的性能，其中感染率表示種子集在SIR 模型下感染節(jié)點占所有節(jié)點的比例；感染時間代表種子集在SIR 模型下達到最大感染率所需時間，驗證IMNE 算法是否在SIR 擴散模型下使得影響力擴散范圍在較短時間內(nèi)達到最大。令NI表示在影響力擴散過程中從易感染狀態(tài)轉(zhuǎn)變?yōu)楦腥緺顟B(tài)的節(jié)點數(shù)量，|V| 表示整個HIN 包含的節(jié)點數(shù)量，則感染率定義為

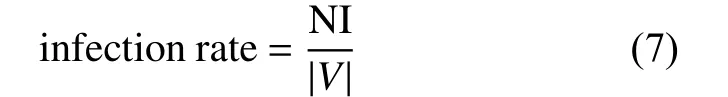
通常情況下，感染率越大、感染周期越短，算法性能越強。

2)在線性閾值模型實驗中，將使用種子節(jié)點激活的其他節(jié)點數(shù)目來評估不同算法的性能，激活的節(jié)點數(shù)量越多，表示該影響力最大化算法的性能越強。

3.2 IMNE 算法在SIR 模型下的性能

本節(jié)將從感染率和感染時間兩個方面分析IMNE 算法在SIR 模型下的有效性。

1)最大感染率。

由于存在隨機性，每次實驗中被感染節(jié)點的數(shù)量通常不同，因此本實驗將每組種子集在SIR模型上運行50 次，取平均感染率作為該組種子集的感染率。圖4 顯示了不同算法的top-k個不同類型的影響力節(jié)點獲得的感染率。

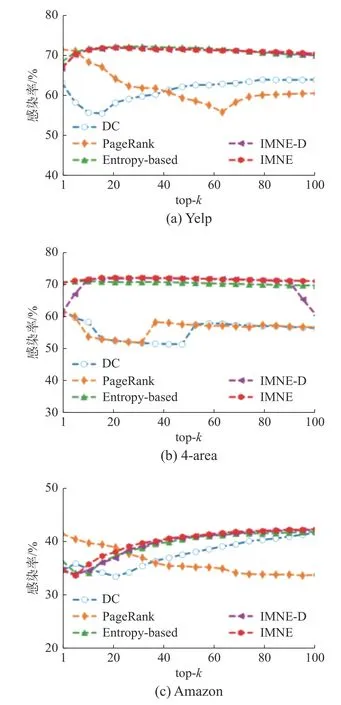
圖4 不同算法的top-k 影響力節(jié)點的感染率比較Fig.4 Comparison of infection rate of different methods with different top-k influential nodes

首先，從圖4 可以看出，IMNE 算法得到的感染率優(yōu)于基線算法(DC、PageRank 和Entropybased)，這表明不同類型節(jié)點之間具有影響且這些異質(zhì)信息有益于影響力最大化。其次，由于不同數(shù)據(jù)集數(shù)據(jù)的分布情況不同，相同的方法在不同的數(shù)據(jù)集上具有不同的感染率。特別地，DC 和PageRank 更加依賴于數(shù)據(jù)的分布情況，例如4-area中節(jié)點度的差異比Amazon 和Yelp 更明顯，因此，在4-area 中PageRank 的性能比在Amazon 和Yelp 更穩(wěn)定。同時，還可觀察到，當k值較小時，在Yelp 數(shù)據(jù)集中，Entropy-based 優(yōu)于IMNE 算法，但是隨著k值的增加，IMNE 算法的感染率逐漸優(yōu)于Entropy-based。

其次，關(guān)于IMNE-D，其與IMNE 的主要區(qū)別在于影響力度量組件，IMNE-D 僅考慮了直接鏈接節(jié)點之間的影響，忽略了社交網(wǎng)絡(luò)中朋友的朋友之間的某種間接影響。根據(jù)結(jié)果(IMNE>IMNE-D)，可以發(fā)現(xiàn)間接影響力對改善影響力的傳播范圍具有重要意義。

2)達到最大感染率的時間。

影響力最大化不僅要求種子節(jié)點的影響范圍最廣，還要求在短時間內(nèi)達到影響力擴散范圍最廣，因此，本實驗從感染時間驗證IMNE 算法的性能。圖5 顯示了不同模型的top-k影響力節(jié)點達到最大感染率的周期（周期即種子完成一次感染和恢復所需時間），可以看出IMNE 算法在3 個數(shù)據(jù)集上的影響力傳播過程中，尤其是Yelp 和Amazon，IMNE 達到最大感染率的時間均小于其他基線算法，表示IMNE 算法能在較短的時間內(nèi)達到較大的感染率,即IMNE 算法具有效性。在4-area 數(shù)據(jù)集中，當k值超過60 時，盡管IMNED 感染時間小于IMNE，但此時從圖4 可以發(fā)現(xiàn)IMNE 算法的感染率大于IMNE-D。

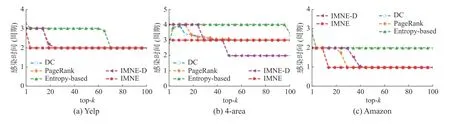
圖5 不同算法的top-k 影響力節(jié)點感染時間比較Fig.5 Comparison of infection time of different methods with different top-k influential nodes

綜上所述，通過分析最大感染率和達到最大感染率所需時間，可以發(fā)現(xiàn)，IMNE 算法相較于其他基準算法能在更短的時間實現(xiàn)影響力最大化。

3.3 IMNE 在線性閾值模型下的性能

為了更好地驗證IMNE 算法的有效性，本實驗也驗證了IMNE 算法在線性閾值模型下的有效性。圖6 顯示了在4-area 和Yelp 數(shù)據(jù)集上不同算法的k=(5,10,20,30,40,50) 個有影響力作者的影響范圍。

從圖6 可看出，IMNE 算法的影響范圍均大于同質(zhì)網(wǎng)絡(luò)中的方法(DC、Entropy-based 和PageRank)，這表明IMNE 算法在LT 模型下也能較好地實現(xiàn)影響力最大化。其次，IMNE 算法的影響范圍接近MPIE 算法，這表明IMNE 算法可以在不指定特定的元路徑的情況下也能較為有效地度量HIN 中節(jié)點的社會影響力。

圖6 不同算法的top-k 影響力節(jié)點影響范圍Fig.6 Comparison of the range of top-k influential nodes of different methods

3.4 計算效率

本實驗主要從節(jié)點社會影響力的計算時間分析IMNE 算法的效率。表1 展示了不同算法在4-area、Yelp 和Amazon 數(shù)據(jù)集上計算節(jié)點社會影響力耗費的時間。

首先，從表1 可以看出，由于不同數(shù)據(jù)集的數(shù)據(jù)分布情況不同，不同算法在不同數(shù)據(jù)集上的計算時間不同，IMNE 算法和其他基準算法在Yelp 數(shù)據(jù)集上的計算時間最少，4-area 數(shù)據(jù)集上的計算時間最多。

表1 不同算法的計算時間比較Table 1 Comparison of computation time of different algorithm s

其次，IMNE 算法花費的計算時間高于同質(zhì)網(wǎng)絡(luò)中的方法(DC、PageRank 和Entropy-based)，這是因為IMNE 算法既考慮了HIN 中節(jié)點的異質(zhì)性又度量了節(jié)點的直接影響力和間接影響力，而DC、PageRank 和Entropy-based 忽略了HIN 中節(jié)點類型和邊類型，僅做簡單的計算；IMNE 算法的計算時間少于MPIE 算法，這是因為MPIE 算法需要迭代計算不同元路徑下節(jié)點的社會影響力進行融合，而IMNE 算法通過網(wǎng)絡(luò)嵌入已將HIN 映射于同一向量空間，節(jié)省了社會影響力的計算時間。

通過分析IMNE 算法的計算效率和有效性可以發(fā)現(xiàn)，IMNE 算法不僅相較于其他基準算法能在更短的時間內(nèi)實現(xiàn)影響力最大化，而且在社會影響力的計算效率上，也具有一定的優(yōu)勢。

3.5 參數(shù)分析

1)權(quán)重的影響。

圖7 展示了IMNE 算法中直接影響力和間接影響力的各種線性組合對影響力最大化的影響。從圖7(a)、(b)可以看出直接影響力和間接影響力的權(quán)重分別為0.6 和0.4 時，感染率優(yōu)于其他組合。這表明區(qū)分直接影響力和間接影響力對影響力最大化具有重要意義。此外，在Amazon 數(shù)據(jù)集下，不同直接影響力和間接影響力權(quán)重組合，其感染率變化不明顯，這是因為Amazon 是一個密集數(shù)據(jù)集，在密集數(shù)據(jù)集中，具有較高直接影響力的節(jié)點其也具有較高的間接影響力。因此，本文將直接影響力和間接影響力的權(quán)重分別設(shè)置為0.6 和0.4。

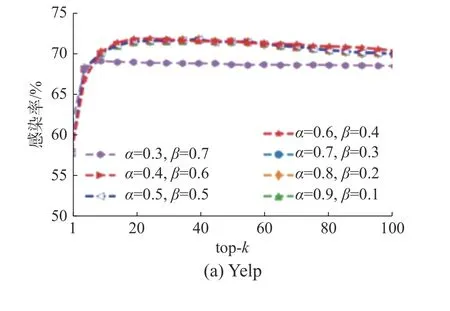
圖7 不同的權(quán)重對IMNE 算法的影響Fig.7 Comparison of IMNE with different weight of direct and indirect influence on three datasets.

2)感染概率 γ 的影響。

SIR 模型主要包含感染概率 γ 和恢復概率θ兩個參數(shù)，本節(jié)實驗測試了感染概率γ=(0.4,0.5,0.6,0.7,0.8,0.9)對IMNE 算法的影響，測試結(jié)果如圖8所示。

圖8 SIR 中不同的感染概率對IMNE 算法的影響Fig.8 Comparison of IMNE with different γ on three datasets.

從圖8 可以看出，隨著感染概率 γ 的增加，感染節(jié)點的比例也增加，這與事實相符。但是，從圖8(a)可以看出，當感染概率分別為0.6 和0.7 時，感染率接近，因此本文選擇0.8 作為感染概率。

4 結(jié)束語

本文提出了一種HIN 中基于網(wǎng)絡(luò)嵌入的影響力最大化算法IMNE，該模型首先基于網(wǎng)絡(luò)嵌入方法將不同類型的節(jié)點映射于低維向量空間，保留HIN 的網(wǎng)絡(luò)結(jié)構(gòu)以及語義信息，使得不同類型節(jié)點處于同一度量空間，然后通過擴展傳統(tǒng)信息熵模型度量HIN 中不同類型節(jié)點的影響力選擇最具影響力的節(jié)點作為種子集，實現(xiàn)了HIN 中的影響力最大化。但本文選擇了已知的SIR 模型和線性閾值模型作為影響力擴散模型，未提出新的擴散模型，在將來的工作中，將考慮提出基于博弈論的擴散模型，不僅考慮網(wǎng)絡(luò)結(jié)構(gòu)對影響力擴散的影響，還考慮信息本身對影響力擴散的影響。

本文的主要貢獻如下：

1) 提出了一種HIN 中基于網(wǎng)絡(luò)嵌入的影響力最大化模型IMNE，該模型利用網(wǎng)絡(luò)嵌入將HIN 中所有節(jié)點映射于同一向量空間，不僅揭示了HIN 中豐富的語義信息，還保留了更多的上下文信息，同時還解決了HIN 中不同類型間的異質(zhì)問題，保持不同類型節(jié)點處于同一度量空間；

2)擴展傳統(tǒng)的信息熵模型，考慮多種社會影響力的影響因素，度量HIN 中不同類型節(jié)點的直接影響和間接影響，有效地描述了社會影響力的復雜性和不確定性。

3)在3 個真實數(shù)據(jù)集和兩個擴散模型上評估了IMNE 算法的性能，實驗結(jié)果表明，IMNE 算法相較于其他基準算法能在更短的時間內(nèi)實現(xiàn)影響范圍最大。