融合分區和局部搜索的多模態多目標優化

胡潔，范勤勤,2，王直歡

（1.上海海事大學 物流研究中心，上海 201306;2.上海交通大學 系統控制與信息處理教育部重點實驗室，上海 200240）

現實生活中的問題往往會涉及多個優化目標，且它們可能彼此沖突、相互制約，這類問題被稱為多目標優化問題(multi-objective optimization problem,MOP)[1]。而多模態多目標優化問題(multimodal multi-objective optimization problem,MMOP)是其中一類較特殊的問題。相比于傳統的多目標優化問題，它在決策空間的多個解可能會有相同的目標值。故多模態多目標優化問題不僅要找到多樣性好和逼近性好的近似帕累托前沿(pareto front,PF)，而且要在決策空間找到盡可能多的等價解[2]。

由于多模態多目標問題在近幾年才受到學者們的重視和研究，故相比于多目標優化算法的研究，其成果相對較少。基于Li[3]提出的無參數小生境算法，Yue 等[4]在此基礎上提出基于環形拓撲結構的粒子群算法(multi-objective particle swarm op timizer using ring-topology，MO_Ring_PSO_SCD)來解決多模態多目標問題，該算法除引入基于索引的環形拓撲結構外，還在決策空間和目標空間中設計一種新的特殊的擁擠距離來進行粒子選擇與更新。結果表明，該算法能定位和保持大量的等價解；Liang 等[5]提出一種自組織多模態多目標粒子群算法(self-organizing multi-objective particle swarm optimization algorithm，SMPSO-MM)。該算法使用自組織映射網絡構建粒子間的鄰域關系并進行鄰域間信息交流；另外引入精英策略避免算法陷入停滯。實驗結果表明該算法能夠定位到更多等價解，決策空間解的分布也較均勻；Li 等[6]提出一種基于適應度排序與強化學習的多模態多目標算法(differential evolution based on reinforcement learning with fitness ranking，DE-RLFR)，該算法首先使用適應度函數聯合排序值確定種群中每個個體的分層狀態，再根據分層狀態確定進化方向和變異策略，最后利用強化學習來引導種群搜索。實驗證明該算法可以顯著提高決策空間中種群搜索效率，在解決多模態多目標問題時有較好表現；Fan 等[7]則使用分區的概念來提高種群在決策空間中的多樣性和降低問題的求解復雜度。研究表明，該方法能夠輔助MO-Ring-SO-SCD 找到更多等價解。Zhang 等[8]提出一種基于聚類的多模態多目標粒子群算法(cluster based PSO with leader updating mechanism and ring-topology，MMO-CLRPSO)。該算法使用決策變量聚類方法劃分子種群，利用帶有領導粒子更新機制的全局粒子群算法獨立地更新每一個子種群的粒子，并在子種群之間建立環形結構探索未被開發的區域以搜索更多的非支配解。實驗結果證明該算法在決策空間與目標空間的解集都能維持較好的多樣性；Liang 等[9]提出一種多模態多目標差分進化優化算法(multimodal multi-objective differential evolution optimization algorithm，MMODE)。該算法使用預選擇機制將所有個體進行適應度值排序后再根據決策空間中的擁擠距離選擇個體進行變異，同時引入新的邊界處理方法將停留在邊界的個體重新調整。實驗結果證明利用 MMODE算法獲得的Pareto 解在決策空間和目標空間中都有一個較好的表現；Liu 等[10]提出一種基于歸檔和重組策略的多模態多目標算法(multimodal multi-objective evolutionary algorithm using two-archive and recombination strategies，TriMOEA-TA&R)。該算法使用決策變量分析技術將種群個體分別歸入多樣性存檔和收斂性存檔中，各自從兩個存檔中選擇父代進行交叉復制。此外，多樣性存檔中使用聚類算法及清除策略來保證目標空間多樣性。最終將兩個存檔的解重組以形成最終解集。實驗結果證明，兩個存檔的分工減少了環境選擇的難度，且算法的整體性能明顯優于比較算法；Lin 等[11]提出一種決策空間和目標空間雙重聚類的多模態多目標進化算法(multimodal multi-objective evolutionary algorithm with dual clustering in decision and objective spaces，MMOEA/DC)。該算法在決策空間和目標空間均采用聚類算法來保持兩個空間的多樣性。在決策空間根據鄰域關系將父代與子代結合并劃分為多個類別，將這些類中獲得的非支配解及其他收斂性好的解對應在目標空間中的解重新劃分為多個類。實驗結果表明該算法能夠有效定位到全局Pareto 解和局部Pareto 解，并且在兩個空間中都有較好的多樣性。Zhang 等[12]提出一種改進的粒子群算法(modified particle swarm optimization,MPSO)求解多模態多目標問題。該算法引入一種基于鄰域的動態學習策略代替全局學習策略，并使用子代競爭機制來提高算法的多樣性。實驗結果證明該算法在多數測試函數上的表現都優于其他比較算法。Li 等[13]提出一種基于高斯采樣(multi objective particle swarm optimization based on gaussian sampling,GS-MOPSO)的多目標粒子群優化算法以求解多模態多目標問題。該算法在搜索前期利用全局高斯采樣方法來進行全局搜索，在搜索后期則采用局部高斯采樣來尋找有潛力解的鄰域。此外，GS-MOPSO 算法采用一種新的外部存檔策略來儲存歷史解。實驗結果表明，該算法能夠找到更多Pareto 解。

雖然諸多學者對多模態多目標進化算法進行改進，但如何保持/提高種群多樣性和提高局部搜索能力來找到更多等價解仍需得到進一步研究。為提高多模態多目標進化算法的性能，本文提出一種融合分區和局部搜索的多模態多目標粒子群算法(multimodal multi-objective particle swarm optimization combining zoning search and local search,ZLS-SMPSO-MM)。在ZLS-SMPSO-MM 算法中，整個決策空間首先被劃分成多個子空間；然后在各個子空間內，自組織映射網絡被用來構建各個子空間的鄰域，并使用協方差矩陣自適應算法(covariance matrix adaptation evolutionary strategies,CMA-ES)來增強算法的局部搜索能力；最后對所有子空間得到的解集進行合并選擇。為驗證所提算法性能，本文選取5 種知名多模態多目標進化算法和14 個多模態多目標問題進行比較與測試。所得實驗結果表明，ZLS-SMPSO-MM 不僅能夠維持種群多樣性以找到更多的等價解，而且能夠在較短時間內找到高質量的解。

1 預備知識

1.1 多目標優化問題

不失一般性，多目標優化問題(以最小化問題為例)的數學形式表示如下[13-14]:

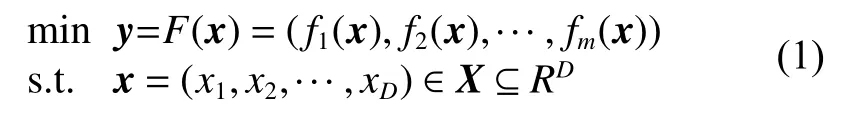
式中：x為D維的決策矢量；X為D維的決策空間；y=(y1,y2,···ym)∈Y?Rm為m維的目標矢量；Y為m維的目標空間。其他一些相關概念如下[15]：

定理1支配關系：向量p支配另一個向量q(記作p?q)的條件是：如果?θ ∈{1,2,···,φ},pθ≤qθ，并且p≠q。

定理2Pareto 最優解集(pareto set，PS)：一個向量x?∈X，若不存在其他向量x∈X，使得F(x)?F(x?)，就稱x?為Pareto 解，所有Pareto 解構成的集合(記作X?)被稱為Pareto 解集。

定理3Pareto 前沿：在多目標優化問題中，Pareto 解集對應目標空間中的目標向量被稱為Pareto 前沿，表示為 PF={F(x?)|x?∈X?}。

1.2 多模態多目標優化問題及評價指標

多模態多目標優化問題是一種特殊的多目標優化問題，其主要表現為兩種情況：1)決策空間中每個解都有多個等價解；2)決策空間中部分解有多個等價解[7]。由于多模態多目標優化問題不僅需要在目標空間獲得逼近性及多樣性較好的PF 逼近，也需要在決策空間中獲得足夠多等價解。因此，本文引入帕累托解集近似(pareto set proximity，PSP)[4]和超體積值(hypervolume，HV)[16]這兩種評價指標來評價多模態多目標優化算法的性能。

式中：CR (cover rate)表示所得解集中解個數與真實PS 中解個數的比值，也稱為解的覆蓋率；IGDx 表示決策空間中的反向世代距離和是算法獲得的解集PS*中第j個變量的最大值和最小值；是PS 中第j個變量的最大值和最小值；d(b,PS*)是b與PS 中最近點的歐幾里得距離；|PS|表示PS 中解的數量。PSP 主要評價得到的解集PS*與PS 之間的相似性。PSP 的值越大，表示算法得到的等價解越多，算法的性能就越好。

2 融合分區和局部搜索的多模態多目標粒子群算法

2.1 分區搜索

對于求解多模態多目標優化問題來說，提高/維持種群多樣性是影響其最后結果的一個重要因素。同時，降低問題求解復雜度也能輔助算法找到質量更好的解。鑒于文獻[7]中所提方法能夠實現以上兩個目標，故所提算法使用分區搜索(zoning search，ZS)來求解多模態多目標優化問題。搜索空間分割步驟：首先從決策空間X的D維優化問題中隨機選取h(1≤h≤D)個變量，將每個變量都分割成l(l>1)段，最終，整個決策空間被分為lh個子空間。

2.2 自組織多模態多目標粒子群算法

在所提算法中，選取自組織多模態多目標粒子群算法[5](self-organizing multi-objective particle swarm optimization algorithm for multimodal multiobjective problems，SMOPSO)為基本的搜索算法，其主要步驟如下：

1)構建自組織映射網絡(self-organizing maps，SOM)。該步驟主要利用SOM 網絡為粒子群算法中的粒子構建鄰域關系，并在根據鄰域關系獲得的神經元集合中選取合適的引導粒子指導種群進化。SOM 網絡構建鄰域關系主要有以下幾步[5,17-18]：

①判斷獲勝神經元。

SOM 網絡中輸入的數據維度為D，將種群的位置信息x=(x1,x2,···xD) 輸入網絡，隱藏層中的每個神經元與輸入層是全連接的結構，所以神經元的權值矩陣的行秩與輸入空間的維度相同，神經元權值矩陣的列秩則與神經元個數相同。因此，整個隱藏層的權值矩陣表示為

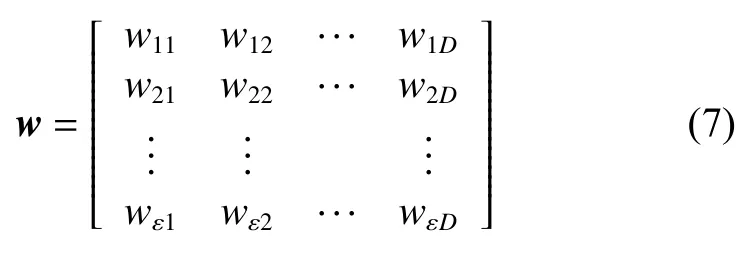
其中ε 代表SOM 網絡中神經元個數。

競爭過程就是找到與輸入向量x最佳匹配的權值向量，等價于找到與向量x歐幾里得距離最小的權值向量，該權值向量所對應的神經元也被稱之為獲勝神經元。其主要公式為

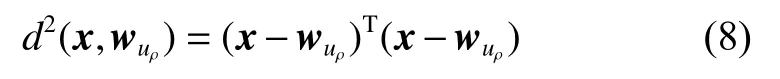
用索引I(uρ) 來標識與輸入向量x最佳匹配的權值向量，其公式為

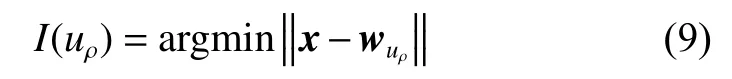
②獲取鄰域神經元信息并更新權值。

根據競爭過程產生的獲勝神經元的索引確定獲勝神經元在隱藏層中的位置，并根據鄰域半徑確定其鄰域神經元。根據已獲得的獲勝神經元的信息更新鄰域神經元的權值信息，權值更新為

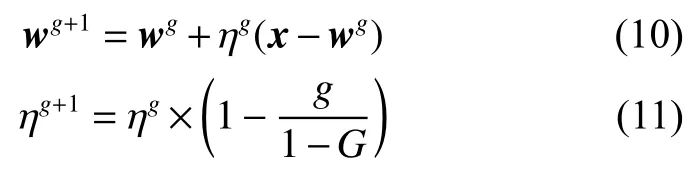
式中：g為當前代數；G為最大迭代代數；η 為學習率。

2)獲得合適的引導粒子。根據1)中構建的SOM 網絡，記錄種群內每個粒子對應的獲勝神經元及每個獲勝神經元的鄰域神經元，將獲勝神經元及其鄰域神經元對應的粒子組成引導粒子的備選庫，并采用非支配排序法選擇排序在第一位的粒子作為當前的引導粒子。

3)粒子速度和位置更新。

式中：v=(v1,v2,···vD) 表示粒子速度；w′為慣性權重；r1和r2是在(0，1)區間正態分布間的隨機數；c1和c2是兩個加速因子；xpbest是個體歷史最優；xnbest是個體鄰域最優。

4)粒子速度和位置超出臨界值修正。在進行粒子速度和位置更新時，若粒子速度超出臨界值，則將其設置為臨界值；若粒子位置超出臨界值，則將粒子位置設置為臨界值并將該點粒子的速度設置為當前速度的相反數。

5)當g≥G時，算法停止。否則回到1)。

2.3 協方差矩陣自適應策略搜索

協方差矩陣自適應策略(covariance matrix adaptation evolutionary strategies，CMA-ES)主要步驟如下[19]：

1)對種群內所有粒子進行采樣。采樣即利用正態分布得到粒子的 λ 個新搜索點作為進入下一代進化的候選解，其采樣公式為

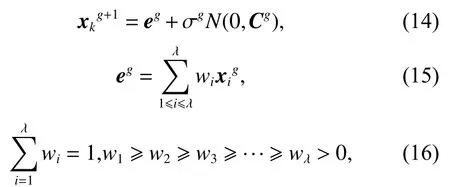
式中：λ ≥2[20]；k代表第g+1代中第k個個體；eg∈Rn是已被挑選入第g代種群的所有個體的加權平均位置；σg∈R+是第g代種群進化的步長；Cg∈RD×D是第g代種群進化的協方差矩陣；N(0,Cg)是均值為0，協方差矩陣為Cg的多元正態分布；wi是采樣后產生的個體的權值。

采樣完成后，重新計算eg+1并設置每個個體的權值，使質量更好的個體有更大概率進行下一步操作。

2)協方差矩陣更新。使用秩-μ 更新模式來計算連續進化代之間的變異步長，并調整協方差矩陣。協方差矩陣的更新分為兩個部分，第1 部分是對進化路徑進行更新，公式為

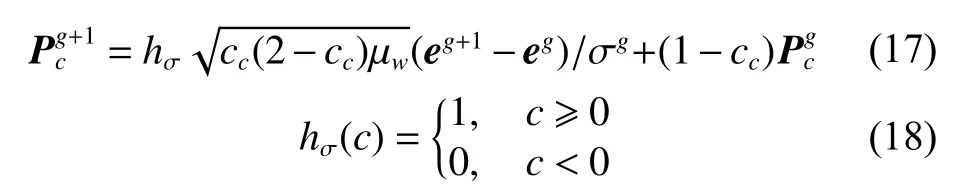
式中：hσ為Heaviside 函數；cc為權值系數；μw為方差有效選擇質量[20]。第2 部分是對協方差矩陣進行更新，公式為

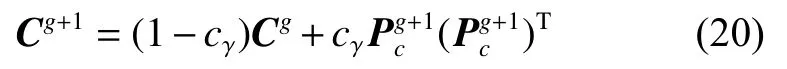
其中cγ是協方差矩陣的學習率。

3)全局步長控制。全局步長控制進化路徑更新與2)的進化路徑相似，公式為

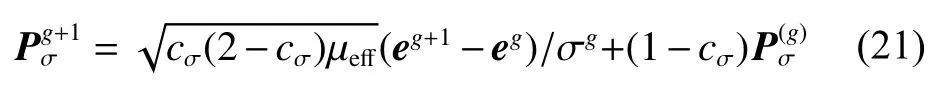
式中：cσ為進化路徑的學習率；μeff為方差有效選擇質量，計算方式與 μw一致[20]。

全局步長更新公式為

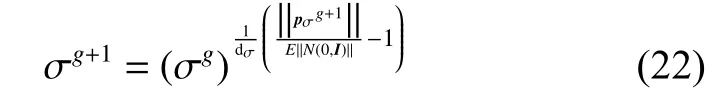
其中dσ是接近阻尼1 的系數。

4) 停止準則。當算法消耗評價次數大于CMA-ES 算法最大評價次數時，算法停止。否則，回到2)。

2.4 融合分區和局部搜索的多模態多目標進化算法

基于2.1～2.3 節，融合分區和局部搜索的多模態多目標算法的具體實現步驟如下：

輸入種群規模NP；算法最大評價次數A；分區數量zn；粒子群參數w、r1、r2、c1、c2；子空間外部存檔容量Q；CMA-ES 算法參數cγ、cc、cσ、局部搜索步長 σ、單個個體進行CMA-ES 搜索消耗的最大評價次數A1；單個個體進行CMA-ES 搜索消耗的累計評價次數A2；CMA-ES 算法加入時消耗的算法總評價次數A3；算法累計評價次數A4。

輸出PS*和PF*。

1)初始化種群x=(x1,x2,···xNP)，子空間外部存檔Q，A1=12，A2=0，A3=0，A4=0；CMA-ES 算法其他參數與文獻[19]保持一致。

2)根據2.1 節對決策空間進行分割，得到4 個子空間。

3)在各個子空間中使用2.2 節的多模態多目標進化算法進行搜索。

4)當A3=0 時，分別對各個子空間中得到的非支配解使用2.3 節的局部搜索算法。當單個粒子消耗的累計評價次數大于A1時，該粒子的局部搜索過程結束。下一粒子繼續進行局部搜索。直到NP 個粒子完成局部搜索，或者A4≥A時局部搜索結束。

5)每個參與局部搜索的粒子與其產生的子代均使用基于特殊擁擠距離的非支配排序法[4]進行排序，排在第一位的粒子取代原本參與局部搜索的粒子進入粒子群，其余非支配解均加入外部存檔。當外部存檔內的非支配解個數大于外部存檔容量Q時，繼續使用基于特殊擁擠距離的非支配排序法進行排序，將前Q個解保留。若外部存檔內非支配解個數小于Q，則全部保留。

6)循環3)～5)，直到A4≥A1時跳出循環。

7)將每個子空間內最后一代粒子群與子空間外部存檔合并，使用基于特殊擁擠距離的非支配排序法選出每個子空間的非支配解。將4 個子空間的解集合并后使用環境選擇得到最終解集PS?=selection(PS1?∪PS2?∪PS3?∪PS4?)和近似帕累托前沿 PF?=selection(PF1?∪PF2?∪PF3?∪PF4?)。

3 實驗結果與分析

3.1 測試函數

為驗證ZLS-SMPSO-MM 的性能，本文選取14 個多模態多目標優化問題對其進行測試。其中，8 個MMF 問題[4]、3 個SYM-PART 問題[21]、3 個OMNI 問題[22]，詳情見表1。所有優化問題的目標個數均為2，MMF 問題與SYM-PART 問題的空間維度為2，OMNI 問題的空間維度分別為3、4、5。PSs 的數量表示決策空間中的不同PS 對應目標空間同一個PF 的數量，PSs 的數量越大，問題的求解難度也會相應增大。最后一列表示的是PSs 在決策空間的每一維度是否重疊，一般情況下，PSs 在決策空間的重疊會增加問題的復雜度。

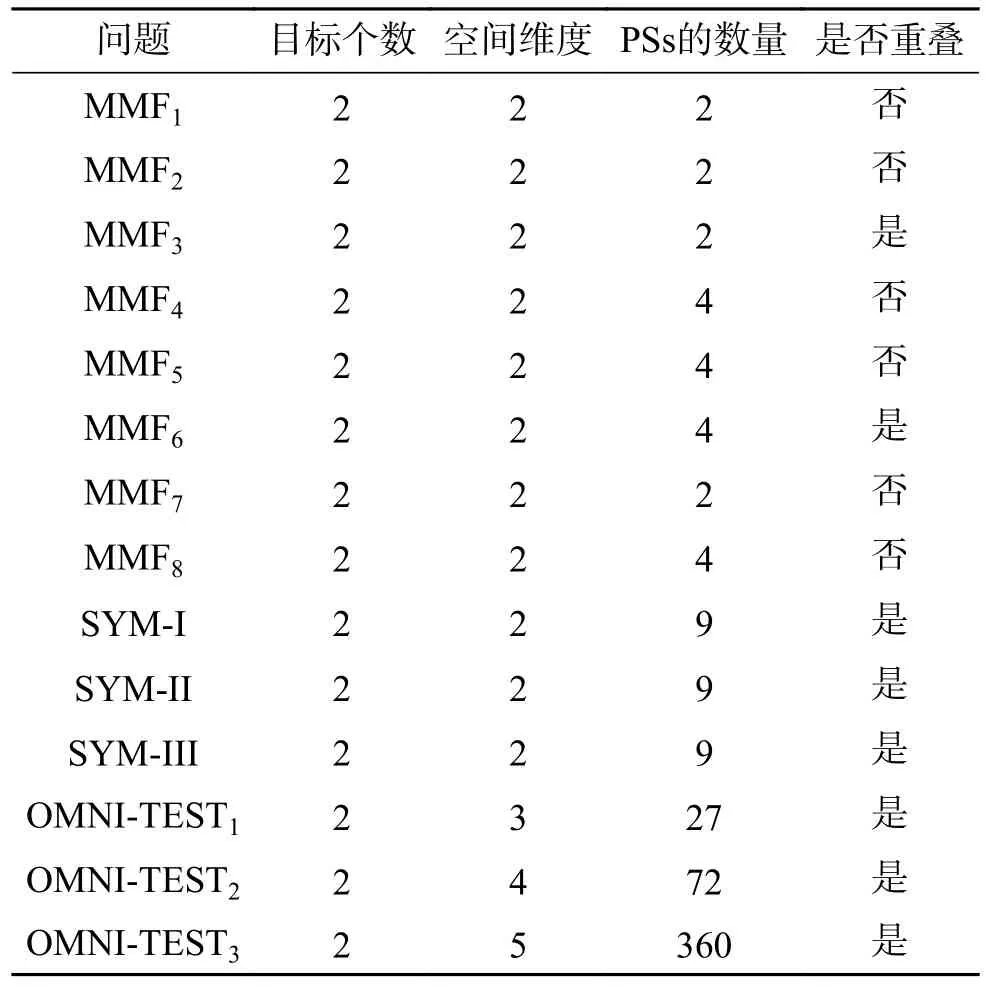
表1 多模態多目標優化問題的相關特征Table 1 Features of multimodal multi-objective optimization problems

3.2 實驗設置

為驗證ZLS-SMPSO-MM 的性能，本文選取5 種多模態多目標進化算法來進行比較。其分別是DN-NSGA-II[2]、Omni-optimizer[22]、MO-Ring-PSO-SCD[4]、SMPSO-MM[5]、Zoning-MO-Ring-SCDPSO[7]。同時，所有比較算法的參數設置與原文獻一致。本實驗中所有測試函數均為2 目標問題，所有測試函數的種群數量均設置為800，最大評價次數為80 000，單個粒子使用CMA-ES 算法的評價次數設置為12。外部存檔容量設置為800。每種算法在測試函數上均獨立運行20 次。為保證實驗結果分析的可靠性，采用Wilcoxon[23]和Friedman[24]非參數檢驗方法對實驗結果進行統計分析，顯著性水平設置為5%。其中“+”、“?”分別表示所提算法優于、劣于相比較算法；“≈”表示所提算法與相比較的算法性能相近。

3.3 結果對比

ZLS-SMPSO-MM 與其他5 種比較算法所得PSP 值的平均值和標準方差見表2。同時，由Wilcoxon 得到的統計分析結果也在表2 中顯示。從表2 可以看出，所提算法在14 個測試函數上所得結果都要顯著好于DN-NSGA-II、Omni-optimizer、MO-Ring-PSO-SCD、ZS-MO-Ring-SCD-PSO。相比于SMPSO-MM，除在MMF3函數上取得相似的結果，ZLS-SMPSO-MM 在其他測試函數上都能得到更好的結果。同時，這6 種算法得到的PSP 值排序結果如下表3，在該表中，利用Friedman 非參數檢驗方法對實驗結果進行統計分析時，將所有算法得到的測試函數的PSP 值均取為其相反數，故排序值越小，算法性能越佳。根據表3 結果可得，ZLS-SMPSO-MM 在所有比較算法中性能最佳。這是因為使用多模態多目標進化算法進行搜索前先使用分區策略劃分了決策空間。在各個互不重疊的子空間區域使用相同規模的粒子群分別進行空間搜索，提升種群多樣性的同時也降低了各個子空間的搜索難度；每個子空間內都引入局部搜索算法，在每次全局搜索后的潛力區域用局部搜索能力強的CMA-ES 算法進行精細搜索，因此能夠找到更多高質量的解。

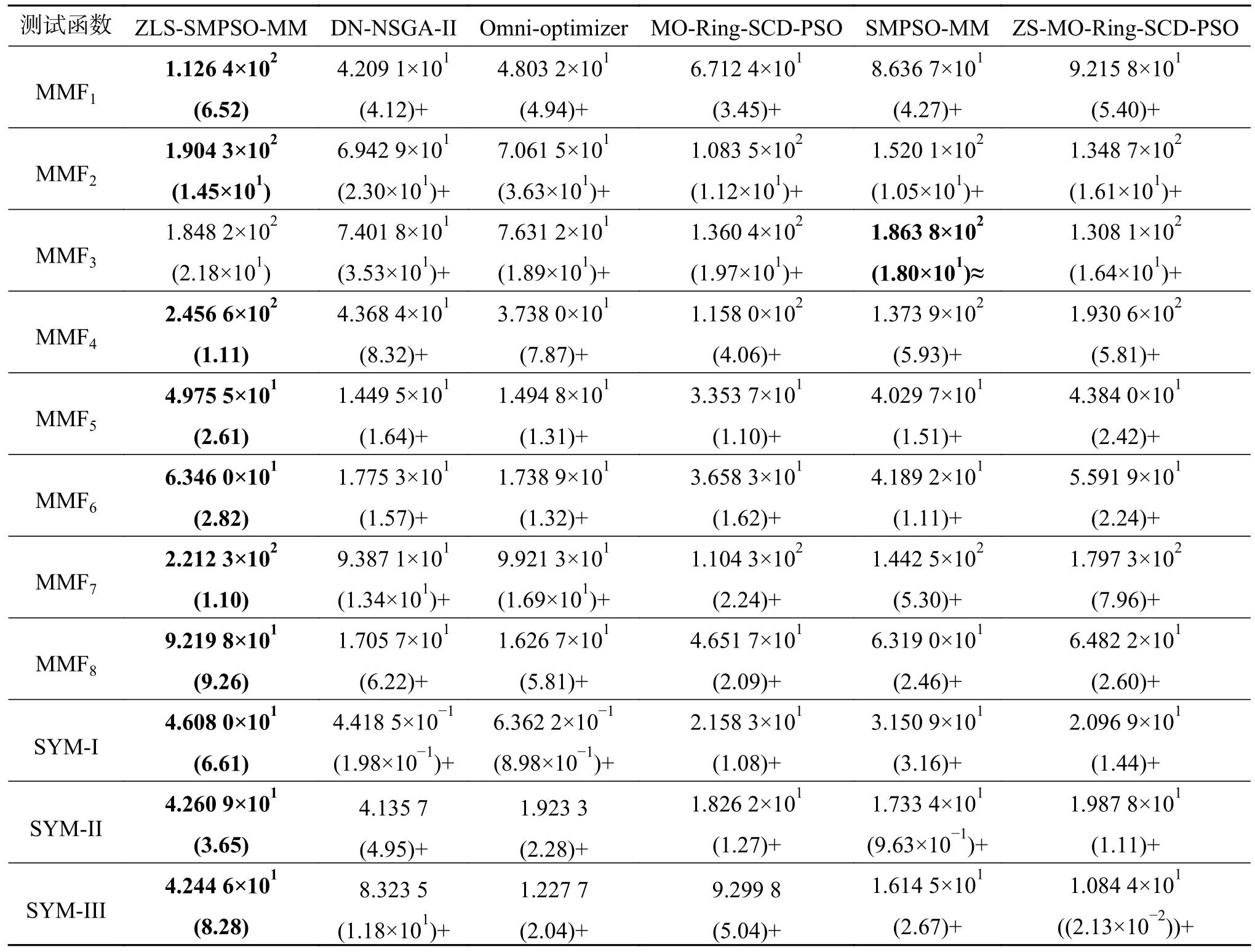
表2 不同算法得到的PSP 平均值與標準方差Table 2 PSP average and standard deviation values obtained by different algorithms

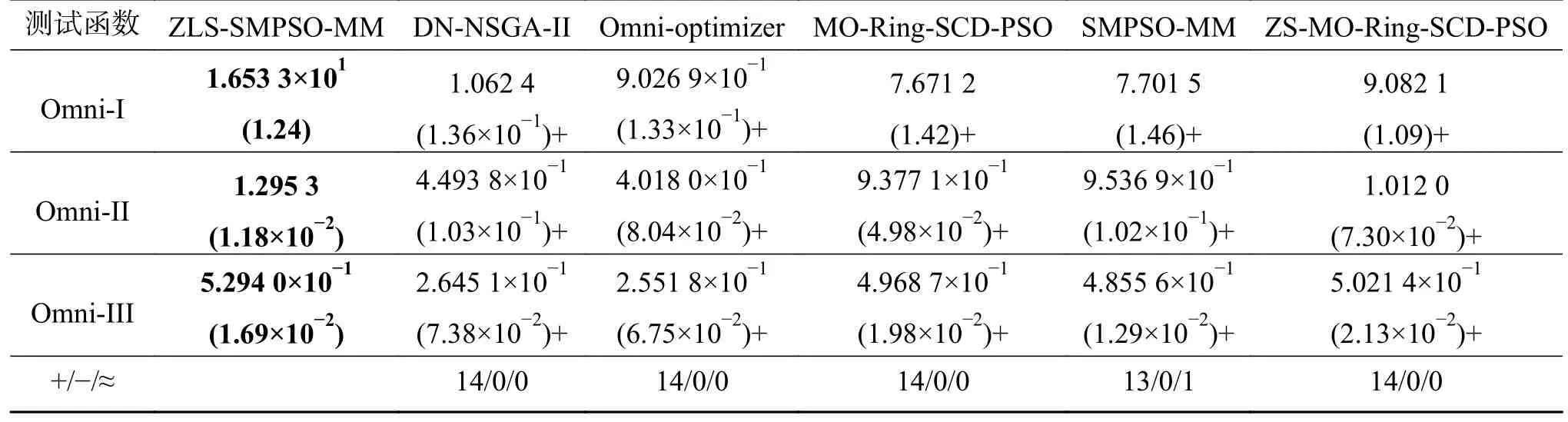
續表 2

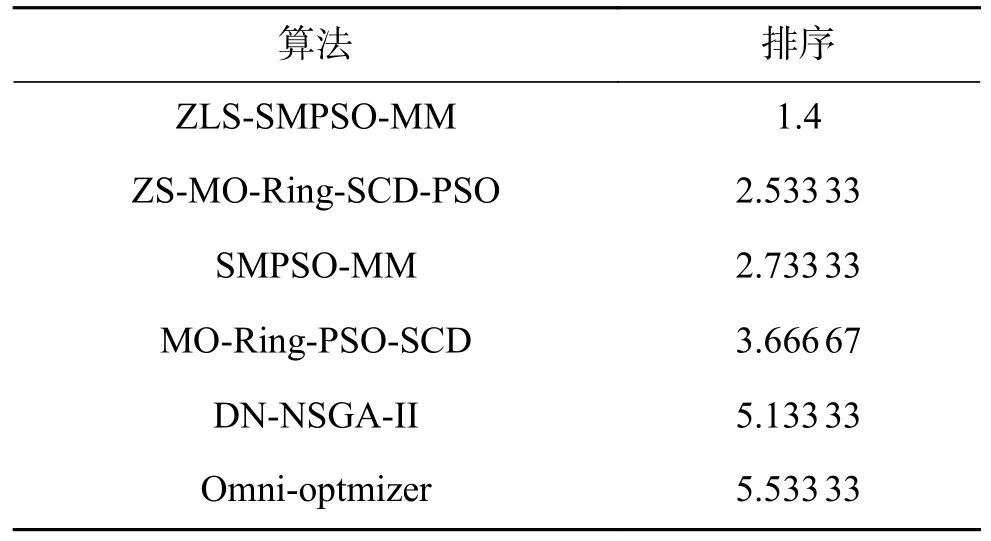
表3 所有比較算法在PSP 上的性能排序Table 3 Performance rankins of all compared algorithms on PSP

ZLS-SMPSO-MM 與其他5 種比較算法所得HV 值的平均值和標準方差見表4。同時，由Wilcoxon 得到的統計分析結果也在表4 中顯示。從表4 中可以看出，ZLS-SMPSO-MM 只在MM7、SYM-I、SYM-II、SYM-III 和OMNI-I 這5 個測試函數中得到較好的結果，Omni-optimizer 則在剩余的9 個測試函數中占優勢，但它們之間的數值差異并不是很顯著。這6 種比較算法得到的HV 值排序結果見表5，ZLS-SMPSO-MM 排在第二位。主要原因是ZLS-SMPSO-MM 中采取的分區策略和局部搜索只能改變算法在決策空間的性能，對目標空間的影響十分有限。目標空間中仍舊采取了之前的選擇策略，因此性能提升效果不明顯，但相對于除Omni-optimizer 外的其他算法，所提算法在目標空間的表現還是要優于其他4 種算法。因此，若是想提升算法在目標空間的性能就必須在目標空間中使用合適的多目標處理技術。

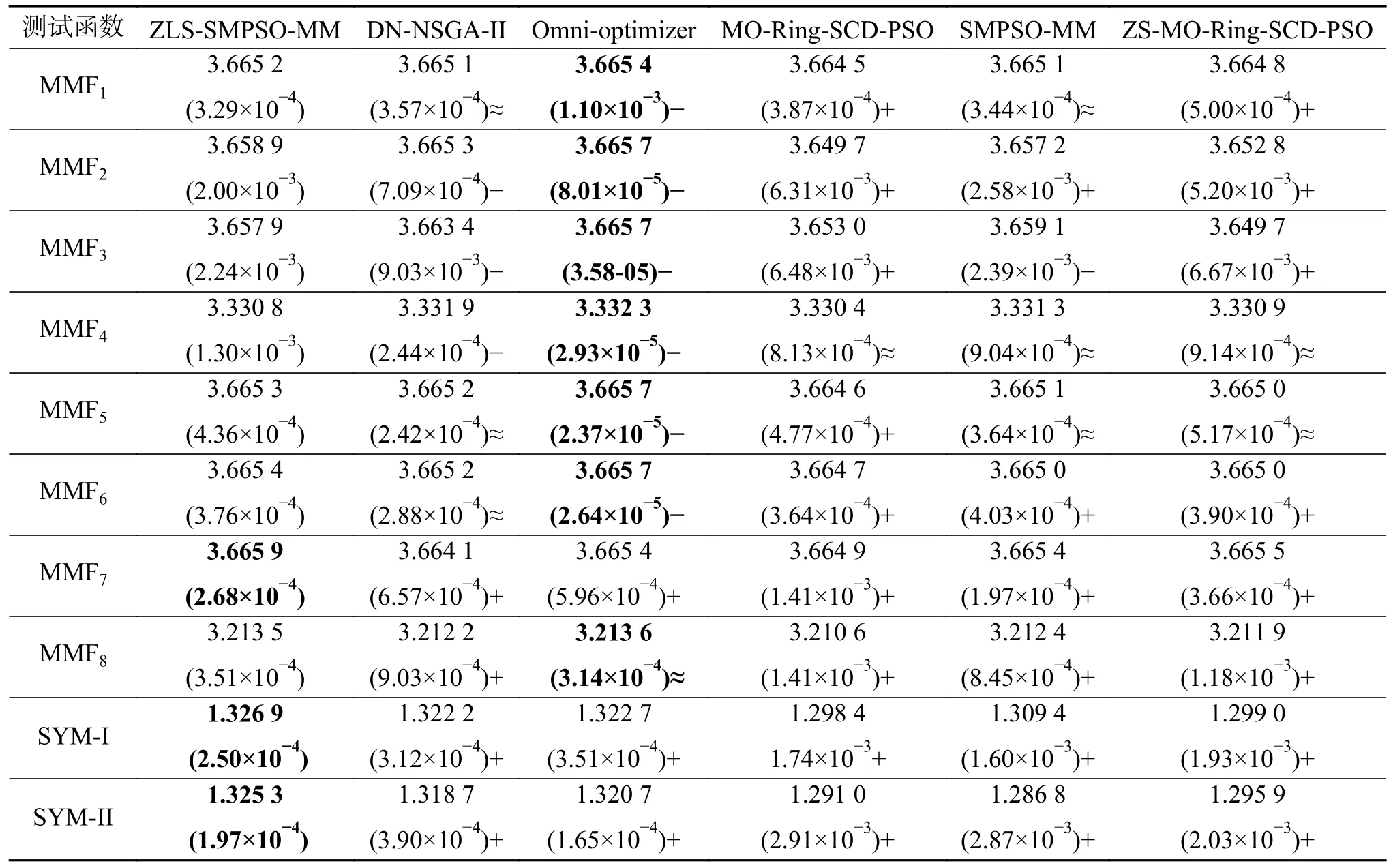
表4 不同算法得到的HV 平均值與標準方差Table 4 HV average and standard deviation values obtained by different algorithms

續表 4

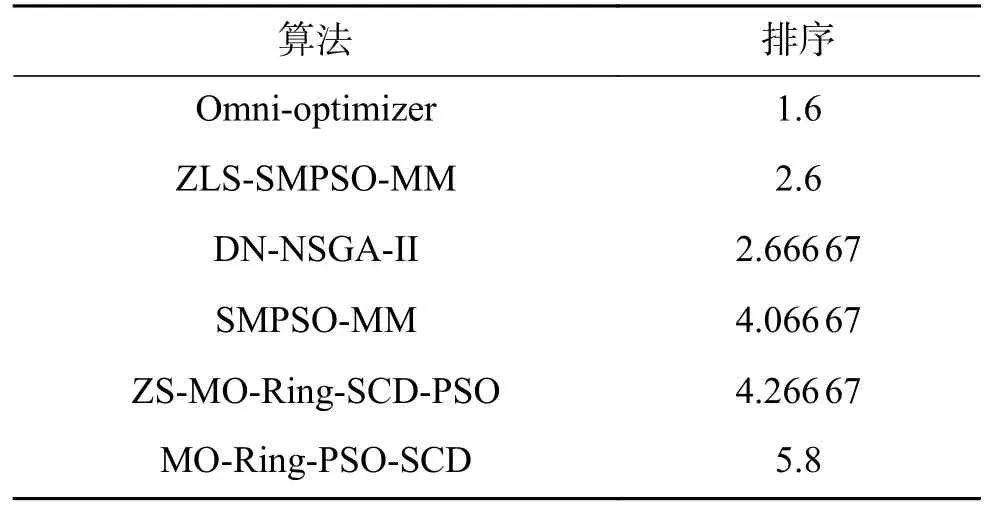
表5 所有比較算法在HV 上的性能排序Table 5 Performance rankins of all compared algorithms on HV

綜合各算法的PSP 值和HV 值實驗結果，所提ZLS-SMPSO-MM 算法獲得的帕累托解集能夠較好地逼近真實帕累托前沿，相比于其他算法具有更好的收斂性和多樣性。

3.4 算法分析

3.4.1 分區搜索與局部搜索對算法的影響

為驗證分區搜索與局部搜索的有效性，該部分實驗分別選取沒有分區搜索和局部搜索的SMPSO-MM、有分區搜索但沒有局部搜索的SMPSO-MM(命名為ZS-SMPSO-MM)來和所提算法進行性能比較。同時，所有算法參數設置與3.2 節一致；并挑選3.2 節14 個測試函數進行實驗，所得結果見表6。

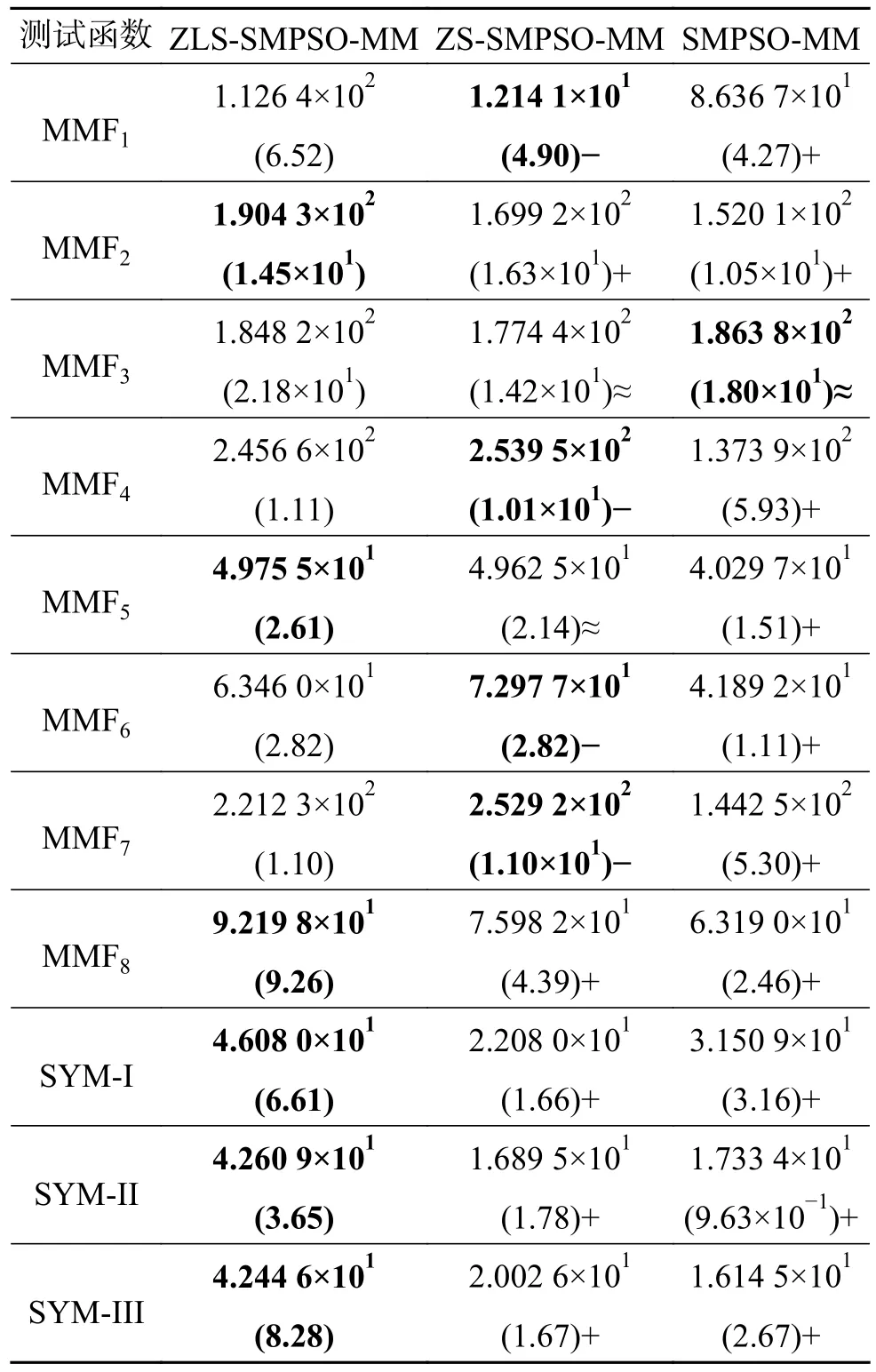
表6 SMPSO-MM 及其變種得到的PSP 平均值與標準方差Table 6 PSP average and standard deviation values obtained by SMPSO-MM and its variant algorithms

續表 6

從ZLS-SMPSO-MM 和ZS-SMPSO-MM 的結果來看，除M M F1、M M F4、M M F6、M M F5、MMF7這5 個測試函數外，ZLS-SMPSO-MM 在其余測試函數上得到的PSP 值均明顯優于ZSSMPSO-MM，尤其是在較復雜的SYM 函數與OMNI 函數上。這說明局部搜索策略能夠有效輔助多模態多目標進化算法找到更高質量和更多的等效解。從ZLS-SMPSO-MM 與SMPSO-MM 的結果來看，除MMF3測試函數外，所提算法能夠在所有測試函數上取得更佳效果。這表明分區搜索和局部搜索能夠有效幫助SMPSO-MM 算法找到更多的等價解。主要是由于分區搜索能夠維持算法種群多樣性和降低問題求解難度，而局部搜索能夠提高搜索精度。另外，從ZS-SMPSO-MM與SMPSO-MM 的結果來看，除MMF3、SYM-I、SYM-II 這3 個測試函數外，其余測試函數的PSP值均顯著優于SMPSO-MM，從實驗結果可知，分區搜索能夠幫助SMPSO-MM 算法定位到更多的等效解，該結論與文獻[7]一致。

由于測試函數的帕累托解在整個決策空間并非均勻分布，因此均衡的分區策略會浪費一些計算資源，如測試函數MMF3，SMPSO-MM 加入分區搜索后，其PSP 值反而下降。但總體來說，同時使用分區搜索與局部搜索能夠提高算法求解多模態多目標問題的能力。

3.4.2 局部搜索評價次數A1敏感值分析

由于局部搜索會消耗一定的計算量，局部搜索過多消耗計算資源可能使算法全局求解能力下降，而過少消耗計算資源則可能導致局部搜索算法能力發揮不足。故本部分對單個粒子進行局部搜索使用的評價次數進行分析，并用PSP 性能指標來對實驗結果進行評價。選取3.1 節的14 個測試函數進行實驗，并將單個粒子進行局部搜索使用的評價次數A1設定為4、8、12、16，其他參數設定同3.2 節。

所得結果使用Friedman 測試來進行性能排序，見圖1。從圖1 中可以看出，一開始隨著局部搜索評價次數的增加，算法的性能也會得到相應的提升，但隨著評價次數增加到一定的程度，算法的性能反而會降低。這是因為合適的局部搜索評價次數能平衡局部搜索能力與全局搜索能力。另外，根據圖1 的結果顯示，當A1=12 時，算法的性能表現最佳，因此在所提算法中將A1設置為12。

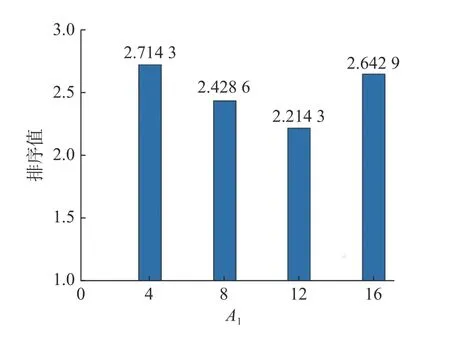
圖1 A1 對所提算法的影響Fig.1 Impact of A1 on the proposed aglroithm

3.4.3 局部搜索評價次數A3敏感值分析

使用局部搜索的時間對算法性能會產生影響。直觀來看，過早使用局部搜索會因為所尋得的區域潛力不足而浪費計算資源，過晚使用則可能無法發揮局部搜索的真正作用。因此，本節對局部搜索的使用時間進行分析，并用PSP 性能指標來對實驗結果進行評價。選取3.1 節的14 個測試函數進行實驗。將局部搜索的使用時間設置為算法已消耗的評價次數。使用時間分為A3=0、A3=2 000、A3=4 000和A3=6 000。除該參數外其余實驗參數設置同3.2 節。

所得結果使用Friedman 測試來進行性能排序，見圖2。從圖2 中可以看出，在種群進化前期加入局部搜索能夠更加有效幫助算法找到更多的等效解。其主要原因是局部搜索能夠在較短時間內輔助多模態多目標進化算法找到高質量的解。當然，這完全取決于算法能否在進化前期就能找到有潛力的搜索區域。另外，圖2 表示當算法已消耗評價次數不小于2 000 時，其能使所提算法性能達到最佳，因此在所提算法中設置A3=2 000。

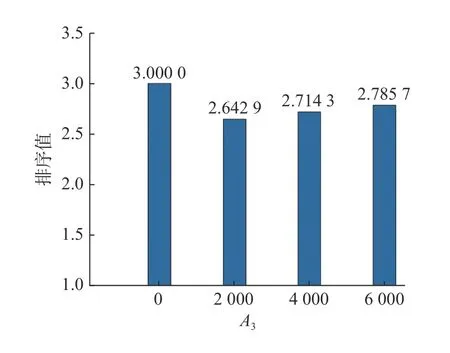
圖2 A3 對所提算法的影響Fig.2 Impact of A3 on the proposed aglroithm

3.4.4 種群規模敏感值分析

為分析種群規模對算法的影響，本實驗選取第3.1 節的14 個測試函數；使用PSP 作為算法性能評價指標；并將種群規模分別設定為400、800、1 200、1 600，其他參數設定同第3.2 節。最大評價次數均為80 000。

所得結果使用Friedman 測試來進行性能排序，見圖3。從圖3 中可以看出，隨著種群規模的增加，算法的性能逐漸降低。其主要原因是，雖然大的種群規模可以提高各個分區的種群多樣性，但在計算資源有限的情況下，搜索代數會減小，這將直接影響算法的搜索效率。同時，當算法種群規模在400 時，算法的性能最佳。但為與第3.2 節中比較算法的種群規模保持一致，所提算法的種群規模仍設置為800。

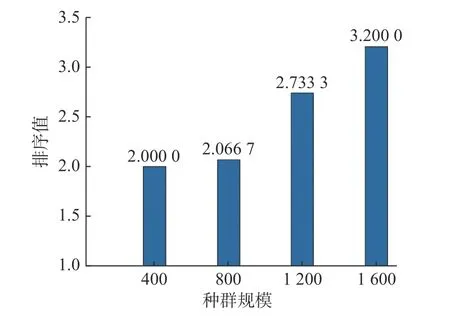
圖3 種群規模對所提算法的影響Fig.3 Impact of population size on the proposed aglroithm

4 結束語

為提高多模態多目標進化算法在搜索過程中的種群多樣性和搜索等價解的能力，本文提出一種融合分區和局部搜索的多模態多目標粒子群算法ZLS-SMPSO-MM。在該算法中，首先將整個搜索空間分成多個子空間，然后使用多模態多目標粒子群算法對各個子空間進行搜索，并使用局部搜索來提高算法的搜索效率，最后將各個子空間所得解集進行合并選擇。為驗證ZLS-SMPSOMM 算法的性能，選取14 個多模態多目標優化問題，并將其與DN-NSGA-II、Omni-optimizer、MORing-PSO-SCD、SMPSO-MM、ZS-MO-Ring-SCDPSO 等多模態多目標算法進行比較。實驗結果表明，分區搜索和局部搜索能夠有效幫助SMPSOMM 找到更多的等價解。