設計有效活動，促進深度學習

周小輝

中圖分類號：G4 文獻標識碼：A 文章編號：（2021）-03-295

隨著新課程改革的不斷深入，教師的教學理念不斷更新，教學技術日新月異，但是依然存在教學方式守舊，脫離學生實際的現象，部分教師缺乏對教學內容的深度理解，只會照本宣科教教材，造成了學生的學習浮于水面，缺乏深度學習。縱觀我們身邊的數學課堂，觀念過于陳舊保守、探究輕描淡寫、忽視知識聯系、輕視思維訓練等問題依然大量存在。

深度學習就是學習者積極主動地學習，積極地探索、反思和創造，學習者在深刻理解的基礎上記憶知識，能掌握知識之間的聯系，并能將知識遷移、應用到新的情境中，做出決策和解決問題。蘇霍姆林斯基曾說：“兒童的智慧在他們的指尖上。”教師在日常教學活動中應設計有效的數學活動，讓學生在動手操作的過程中體驗數學結論與規律的得出過程，親自體驗問題情境，領略數學的奧妙，讓學生學會自覺地運用數學知識去觀察、分析、概括實際問題，揭示其數學本質，并轉化為熟悉的數學問題，從而解決問題。

一、身臨其境，促使深入理解

“綜合與實踐”是一類以問題為載體，以學生自主參與為主的學習活動。在學習活動中，學生將綜合運用“數與代數”、“圖形與幾何”、“統計與概率”等知識和方法解決問題。作為以“問題”為載體的實踐活動，它既不同于具體知識點的學習，也不同于教師在課堂中的直接講授，要突出的是在問題引領下學生全程參與的學習活動。教師要積極創設能讓學生親身體驗的活動，調動學生的多種感官參與，提升學生思維的深刻性，使學生逐步完成數學的抽象，深入理解數學知識的本質內涵。

例如，在教學人教版六年級上冊“確定起跑線”這節課時，可以借助實踐活動讓學生參與給跑道畫起跑線的過程。讓兩位學生分別持手推式測繪輪沿著操場上相鄰的跑道走一圈，發現外圈的長度比內圈的長，通過觀察、測量學生會產生問題：“為了比賽公平，終點要相同，起跑線該如何確定？”教師讓學生觀察相鄰兩條跑道的周長，然后引導學生分析：“跑道是由幾條直道和彎道組成的？造成外跑道比內跑道長的原因是什么？”再讓學生研究這些問題，從而發現：“每條跑道的長度由兩條直道和兩條半圓形跑道組成，第一條半圓形跑道的直徑為72.6m，每條跑道寬1.25m，相鄰跑道直徑的相差數是每條跑道寬度的2倍。”在此基礎上，學生就能抓住問題的關鍵信息與隱藏的數量關系，獲得正確的解決問題路徑，學生會發現直道都是一樣長的，兩條跑道的周長差其實就是兩個圓周長差。其次，教師還可以引導學生根據賽跑時的親身體驗來思考：“為什么在彎道時，運動員們要緊貼內跑道跑？”這樣讓學生走入現實情境，通過親身體驗和實踐，促使學生深度思考，將生活實際與數學知識完美融合，用數學原理來解釋生活中的問題，進而提高發現問題、分析問題、解決問題的能力。

二、層層推進，促進深層建構

通過對比，我們發現修訂教材中新增的教學目標加強了動手操作能力的培養，強調數學基本活動經驗的獲得，提倡自主探索的學習方式，注重了數學思想方法的滲透，彰顯了“做中學”的教學理念。通過研讀，筆者認為一線教師在設計教學時，應以此為準則，安排有效的實踐性活動，讓學生真正“做”起來，在“做”中發現規律，并運用規律解決問題。解決問題不應作為教學的最終目的，我們需要高屋建瓴，通過多種維度深入研究一個問題，從一個問題推向一類問題，不斷建構，促進思維的發展。

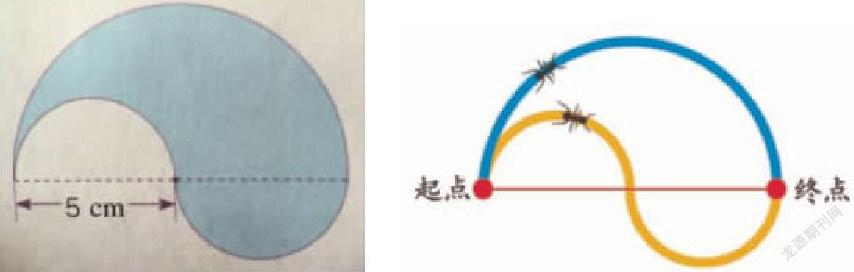
如，在教學周長的內容時，你能認真研讀教材，就會發現修訂教材練習十四中第10題“下面圖形的周長是多少厘米？你是怎樣算的？”和曾經的學生疑惑題“兩只螞蟻賽跑，螞蟻A沿著上面跑道跑，螞蟻B則沿著下面跑道跑。如果兩只螞蟻速度相同，誰會勝出？為什么？”異曲同工。一題是通過探究發現求這個組合圖形的周長即求半徑是5cm的圓周長，一題是探究后發現兩種路線等長。如果只是單純地解決這兩個問題并不是很困難，只需將它們計算出來比比即可。

如果教師在教學時第10題時能從學生感興趣的“螞蟻爬”題出發探究，從疑惑點讓學生“換一組數據再計算”和“用字母代替計算”，結果發現計算的結果都一樣。而且從字母代表的數據中更能發現這個規律。設小圓的直徑為a。那么下面跑道的路徑就是一個直徑為a的圓的周長，就是πa。上面跑道路徑就是半徑為a的半圓周，即2πa÷2=πa。

進而拓展：那如果下面的兩個半圓不一樣大呢？如果再多幾個半圓呢？

學生在探索的過程中，漸漸明白其中的道理，更體會著數學學習的樂趣。最后再出示書本中的習題，從兩種路線的比較中合二為一，求這個復雜圖形的周長其實能化繁為簡，就是求一個圓的周長。在不斷地做中，讓一道看似簡單的問題，由疑問開啟一個不同尋常的意境，讓學生在“做”中經歷思維的成長。

三、瞻前顧后，促進深遠思考

數學教材的編寫是按數學知識的邏輯結構，螺旋上升編排的。但是很多教師卻對教材的整體把握卻沒有引起足夠的重視。筆者認為，教師在進行教學時必須把本單元內容放入整個知識體系，“瞻前顧后”地對比研讀，從整體的角度看問題，較之單一的視角，教師所呈現出來的教學視野肯定是不同的。

解構教材體系，在《圓》單元教學前，學生已經學習過長方形等平面圖形及它們的周長、面積計算，也在一年級下冊直觀地初步認識過圓。本單元是正式學習圓的有關知識，也是小學階段的最后一個認識平面圖形的單元。從研究直線圖形到研究曲線圖形，研究方法的變化和提升對學生而言是一種跨越。他們除了要掌握一些基礎知識，還要感受和學習“化曲為直”、“等積變形”、“極限”等數學思想和方法，進而發展數學思維和問題解決的能力，為后續學習立體圖形“圓柱和圓錐”奠定基礎。

因此，筆者認為在教學設計時，不僅要關注學生原有一維空間和二維空間認知，也要為后續三維空間的培養埋下伏筆。

例如，在教學圓面積公式的推導中，教者不僅可以設計有效的教學活動，通過剪拼、教具或課件等多種手段，讓學生在體驗中發揮想象“等積變形”。利用“無限分割”思想把圓“化曲為直”，轉化成與它面積“無限逼近”的長方形，推導出圓面積計算公式。在體會“無限逼近”的極限思想的同時，為后續圓柱體的體積公式推導積累豐富的活動經驗。還可以設計在課結束前拋出一個探究性問題：你能利用今天學習的知識把圓柱轉化成學過的圖形嗎？在本節課深刻的轉化思想沖擊后，讓學生近距離的遷移和感悟，為后續的學習圓柱的體積計算埋下伏筆，把本課的教學提升到一個新的高度。

借助數學活動將學生引向深度學習，是融合數學課堂教學基本活動與促進學生數學思考的有效手段。在設計教學活動時，教師應有意識地組織學生進行觀察、討論、思考、操作、總結、反思，讓學生感悟數學與生活的聯系，在“做”中積累經驗，在“思”中感悟數學思想，從而理解數學的知識本質，掌握數學的思想方法，積累數學的活動經驗，從而促發深度學習，為學生的可持續發展打下良好的基礎。

（鄞州區邱隘實驗小學）