如何在高中數學教學中培養學生的數學思維能力

丁俊

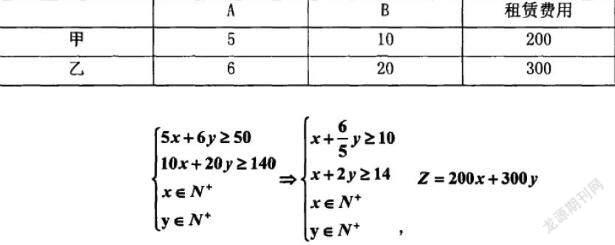
摘 要：隨著新課改的不斷深化，當前的高中數學教育除了培養學生對數學知識內容的了解之外，更將培養學生思維能力作為當前教育的關鍵。教師在引導學生理解數學文化以及數學邏輯思維能力的基礎上，要逐步培養學生的自主創新思維能力，為全面加強高中學生數學核心素養打下堅實基礎。

關鍵詞：高中數學;數學教學;數學思維能力

引言：隨著時代發展以及社會進步，高中教育取得了不少成就，對于青少年的健康發展起到了積極的推動作用，對于高中教學來說，要培養學生的思維能力就要提升學生對數學知識的自主性學習，逐步培養學生的思維能力也是當前高中數學教學最主要的目的之一。

一、高中階段培養學生思維能力的重要意義

一方面，隨著素質教育的提升，人們對于學生思維能力提升給予更多關注。從新課改相關制度開始落實實施開始，素質教育已經獲得當前社會的廣泛認可，與傳統的教育模式對比而言，新的教育模式更能獲得大家的認可。現今高中數學教育不僅需要培養學生對于數學理論知識的認知，還需要培養學生的思維能力，在提升綜合能力的基礎上保障學生全面發展[1]。

另一方面，當前社會也需要具備數學思維能力的人才，因此需要高中課堂加強對學生的培養工作。針對數學學科進行學習時，教師不僅需要注意對于理論知識的引導工作，同時也要加強對實踐能力的培養，數學本身來源于日常生活，在學習過程中要將課堂教學與實踐活動相結合，使得數學成為真正的應用性科學，促使學生自身的思維能力獲得進一步提升。高中數學教學不僅需要重視知識內容的傳授與講解，還需要關注學生自身分析能力、理解能力、抽象思維能力、邏輯思維能力以及創新思維能力等各個方面的發展，同時教師還需要關注學生不同的學習進度以及教學情況，根據不同的學生采用不同的教學方法，切實保障每個學生能在高中數學教學中獲得相應的知識，使得高中數學教學的價值得到更加充分的體現。除此之外，教師本身還需要注意教學模式是否高效，在保障教學內容正確的基礎上帶動課堂教學氣氛，注意學生實際的學習情況，采取更加多元化的教學方式，注意課堂中學生對教學情況的反饋，帶動學生學習數學的熱情，促使學生能夠以更加積極的狀態投入數學學習之中，從而更好地培養學生的數學思維能力。

二、培養高中學生思維能力的主要方法

對數學思維能力的培養很多時候比單純的數學知識更加重要，數學知識是會隨著年齡增長以及職業要求而逐漸被遺忘的，但是數學思維能力則會影響到人們生活的方方面面，要針對數學思維能力進行合理訓練，就能提升人們的生活質量，這同時也是素質教育中最主要的部分之一。因此在高中階段的教學中，教師不僅需要重視數學知識內容的傳授，更需要注意關注對學生數學思維能力的培養。

（一）優化學生認知結構，逐步培養思維能力

1.打破傳統章節限制，重設學生數學知識體系

知識結構是將知識內容與學習經驗進行融合之后形成每個人專屬的知識體系，這也是培養數學思維能力中主要需要落實實踐的內容。高中階段學生學習數學還是以解決問題為主，是較為微觀的角度看待問題，其中涉及的知識點內容則是在宏觀的知識體系中形成的某一個分支，因此要形成宏觀的解題思路，在對數學知識內容有全面認知的基礎上完成自身認知結構的優化，幫助學生厘清思路，尋找與知識點相關的解決方法，解決當前的思路問題，提升學生自身思維的靈活性以及廣闊性。

大部分的高中學生比較重視課前預習，但是在實踐當中卻鮮少有學生針對課程內容進行復習，將題目中蘊含的知識內容以及涉及到的知識點進行歸納總結，這主要就是學生在學習新的數學知識后不會將其納入自身的認知體系中，將知識內容進行規范化梳理，另一部分則是完全依照課本的排序梳理知識內容，無法融入自身認知，打破原有的轉接限制而是以自己的知識體系作為基礎完成順序排列。這就導致不少學生在面對不同數學課程內容是事倍功半且學習效率低下的主要原因[2]。

針對這一現象，高中數學教師應當采取具有針對性的措施，對知識內容進行拆解，培養學生按照知識體系劃分知識內容的應當嵌入的體系內容，優化學生知識結構，提升知識點的有效性，保障學生自身的數學思維能力獲得提升。

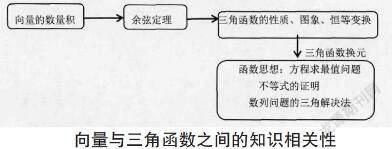
以高中數學必修二中的《第六章平面向量及其應用》為例，如果當前有等腰梯形ABCD，已知AB與DC相平行，同時AC與BD相交于M，AB=2CD=4，，則cos∠BMC是多少？

要解析本題首先需要了解當前知識題目中要用到的建系法以及基底法進行問題求解，教師要在保障學生對向量有全面理解的基礎上進行啟發式的教學，找到與數學知識相關的內容，建立學生自身完善的知識結構體系，在向量數量積相關定理學習基礎上利用余弦定理進行解答，由此可知兩部分的知識內容時存在一定的關聯性的，教師要注意引導學生將各個知識點串聯起來，保障三角函數也能融入向量解題之中[3]。

要形成這樣的知識結構，不僅需要對數學學習內容有全面性認知，還需要教師引導學生打破章節之間的限制壁壘，保障學生理解各項內容之間的相關性，找到切實可行的知識點內容，形成全面性的解題速率，推進學生思維靈活性發展。

2.引導學生針對數學定義、公式進行多角度的思考

高中階段不少學生由于數學學習中定義公式過多，一般都是采取死記硬背的模式進行解題應用，只有很小一部分的學生會關注公式的推演過程。要促進學生數學思維能力的培養，教師就需要引導學生對知識結構有正確的認知，利用架設、猜想以及論證的方式領悟公式或者定義包含的主要內容，改變學生的思維方式，真正找到切實的數學知識立足點，同時能夠借由數學知識之間的關系拓寬學生的數學思考，在提升思維廣闊性的前提下使得學生感受到數學知識內容的魅力[4]。

以高中數學必修二中的《6.4.3余弦定理、正弦定理》為例，三角形ABC中各個角分別是a、b、c，證明余弦定理中的a2=b2+c2-2bccosA，b2=a2+c2-2accosB，c2=a2+b2-2abcosC是否成立，如果教師直接進行證明過程的展示，學生雖然能很快理解題目內容，但是由于缺乏必要的思考過程，很難真正理解其中的思維模式，如果在面對此類問題可能會出現無從下手的感覺，尤其是教學模式中缺乏思維能力培養的過程中，因此就需要以學生作為研究主題，教師作為引導幫助學生找尋探究方向，以達成最終的證明目的。

此處教師可以引導學生采用初中階段就數值的勾股定理對圖形進行變動，根據直角三角形相關內容將其中的證明部分才想出來，針對余弦定理完成永恒最終的證明。由于CD2+BD2=BC2推演出BC2=（c-bcosA）2+（bsinA）2=c2-2bccosA+b2，借此證明余弦定理。

（二）強化學生對實物情境的分析能力

數學問題一般出現的表征方式都是以解題的模式出現的，要調動相應的知識內容診斷題目進行解答是一個思維模式以及符號、圖像轉化的過程，數學問題的表征優劣直接決定了后續學習者對數學內容的認知，在此基礎上教師要設立符合學生自身學習實際的難度，既能夠幫助學生接受更豐富的數學知識，還能夠鍛煉學生自身的數學思維能力。

1.強化學生對實際問題情境化表征問題的解決能力

不少學生在高中數學學習過程中存在認知性錯誤，認為數學的本質就是解決數學問題內容，與現實生活并無緊密的聯系，因此教師在進行教學時要注意引導學生對問題內容有更加深刻的理解。

要落實實物情境完成表征問題教學，一方面要注意針對較為抽象的定理內容教師要加強對學生抽象思維能力的鍛煉。另一方面要促使學生能夠理解高中數學知識內容與實際生活存在的聯系，提升學生自身對于數學模型的構建能力，展示給學生多種多樣的表征問題類型，促使學生參與到解題過程中，從而感知到表征問題的解答對數學思維鍛煉的意義。

2.強化學生對圖形、圖表的表征探究能力

圖像本身有著直觀表述的優勢，但是在高中數學學習中不少問題的提問方式以及最終的解題步驟都需要抽象思維的協助，要將幾何問題與數學問題相結合，從而引導學生進行邏輯思維的正向轉化。

利用圖表進行表征問題的解答，能夠將抽象的數學問題變得更加簡明扼要，學生能夠以圖表規律完成數學問題的解答，形成清晰的邏輯思維能力。

以高中數學必修一中的《第二章二次函數與一元二次方程、不等式》為例，假設某個物流企業分別有甲乙兩款車來源送ab兩種物品，當前甲車能夠運輸a五件貨物以及b八件貨物，乙車每天能夠運輸a六件貨物，b二十件貨物，但是甲每天需要200塊油費，而乙需要300塊油費，如果公司每天至少要送a五十件、b一百四十件才能保障運營，那么一天要花多少油錢？

教師可以引導學生們先將甲類車輛設為x輛，乙類車輛設為y輛，將油費設為z元，列圖表和式子表示當前各項數據之間的關系。

之后教師可以借助公式以坐標系模式列出公式中各項內容，以幾何視角直觀地看出目標函數z所處在焦點位置，從而取值，就能得知最節省油費的運營模式。

（三）提升學生的認知能力，推進思維能力發展

當前大部分高中學生對于課程內容缺乏必要的反思，無法有效推進自身認知能力的進一步發展，尤其是題目之間知識點和邏輯有著強烈聯系，教師應當引導學生重視問題之間的邏輯關系，將指示內容進行匹配，找尋合適的解題方法，舉一反三將問題中涉及到的思維能力進行歸納總結，保障學生自身的知識儲備能夠借此不斷整合優化。

高中階段學生的數學思維能力是需要逐漸培養的，在培養過程中教師要具體分析每個學生的實際情況，根據學生學習特點落實因材施教的教育方針，促使學生自主、自愿地參與到數學學習當中來，保障學生在學習過程中獲取最多的樂趣，從而逐步體會到學習數學的快樂。

參考文獻

[1]吳國升.在高中數學教學中培養學生數學思維能力的策略[J].課程教育研究：學法教法研究，2019，000（005）：119-119.

[2]濮志強.創造性思維能力在高中數學教學中的培養研究[J].科學大眾（科學教育），2018，000（006）：3.

[3]周寶乾.淺談如何在高中數學教學中培養學生的數學思維能力[J].中學課程輔導（教師通訊），2018，000（021）：P.165-165.

[4]楊立睿.高中數學教學中培養學生數學思維能力的實踐探究[J].學周刊，2018，No.363（15）：24-25.