熱負荷作用面為圓形電器件散熱器熱阻數值分析

盧 鑫，張金龍，武振鋒，王良璧

(1. 蘭州交通大學 機電工程學院，蘭州 730070；2. 鐵道車輛熱工教育部重點實驗室(蘭州交通大學)，蘭州 730070)

肋片式散熱器是工程中常見的一種設備，廣泛應用于電子元件，制冷及工業冷卻系統.散熱器上的肋片增大了散熱器與空氣的接觸面積，從而降低了風冷電子元件的熱阻和工作溫度，達到有效散熱的目的.圖1所示的肋片散熱器是目前應用中最常見的一種結構，廣泛應用在電子設備中的功率元器件，如晶閘管、集成電路等，它的結構是由平行的薄板以陣列的形式分布在基板上形成一系列矩形通道，熱負荷作用面形狀普遍為方形結構.

在實際工程應用中，從不同制造商提供的數百種型號的散熱器中為特定設計選擇最佳的散熱器對工程設計者來說是一項比較艱巨的任務.最佳散熱器的選擇往往取決于其綜合性能、尺寸參數、制造成本等多種因素.因此，為了權衡優化多方面的影響因素，需要設計者在選擇過程的早期就能快速容易的預測散熱器的性能.

許多國內外學者針對圖1結構的肋片散熱器散熱特性進行了大量的理論分析與實驗驗證，并得出了許多重要的性能參數和通用性結論.圖1結構散熱器熱源的作用面形狀為方形，熱量的傳遞方式首先從底板通過熱傳導的方式傳遞給肋片，再通過熱對流和熱輻射的形式散去.Muzychka和Yovanovich[1-3]提出了一種適用矩形截面散熱器對流傳熱關聯式.通過關聯式可以求出矩形通道散熱器的摩擦系數f，氣流阻力R及流經整個散熱器的氣流壓力損失，與傳熱學手冊所提供的方法相比較而言，計算結果更接近于實驗數據.Freegah[4]基于CFD數值模擬方法對新設計的半圓銷型板翅式散熱器強化傳熱進行了分析，在平行流和沖擊流作用下比較了不同結構半圓銷翅片的效率、基溫和熱阻，新結構設計為開發電子工業冷卻系統提供很大的潛力.Prajapati[5]對不同翅片高度(0.4 mm～1.0 mm)的矩形并聯微通道散熱器的傳熱和流動特性進行了數值研究，發現翅片高度0.8 mm的傳熱效率最大.Jonsson[6]對七種不同結構散熱片結構進行了綜合研究，散熱片包括板翅、直排式和交錯式板翅，以及交錯式的圓形和方形銷形等.通過研究不同參數對散熱器性能的影響，如風道高度、風道寬度、肋片的高度、厚度和肋片之間的距離等，得出了努塞爾數和無量綱壓降的經驗關聯式.Huang等人[7]提出兩種新型翅片散熱器，即針型翅片和傾斜型翅片散熱器，用于大功率LED燈在自然冷卻條件下的散熱，并對它們的散熱性能進行了數值研究.研究結果表明，兩種新型肋片結構散熱器模型的總熱阻與原模型相比降低了9.0%～15.6%，傳熱系數分別提高了12.6%～35.2%.

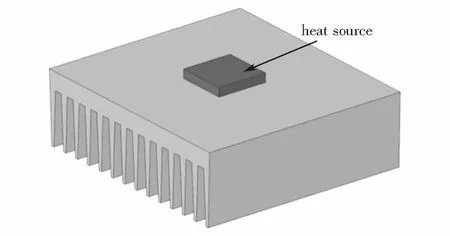
圖1 陣列肋片式散熱器結構 Fig.1 Radiator structure with fin array distribution

Castelan等人[8]建立了平板翅片散熱器在強制對流冷卻條件下的三維分析解模型，求解了散熱器的平均溫度和熱阻，并與數值模擬進行了比較.分析模型與數值模型的平均溫差(ΔT)最大差異為1.4 ℃.該分析解可用于優化設計，以減少現有散熱器的重量，同時驗證了該分析解用于優化冷卻系統的快速性和精確性.趙亮等人[9]對采用數值模擬方法研究了電子器件冷卻常用的平直翅片散熱器及五種針翅散熱器的散熱性能，對比分析了不同來流速度下，不同散熱器的熱阻和流阻特性，得出相比于圓柱針翅、方柱針翅、75°斜柱針翅和60°斜柱針翅，45°斜柱針翅的熱阻最小，但是其流阻增幅更大；增加針翅翅片的厚度能夠有效降低熱阻，但是其流阻增幅也更大；因此在針翅結構設計過程中，應選用較薄的方柱針翅、75°斜柱針翅或60°斜柱針翅結構.

綜上所述，在電子元件肋片式散熱器性能的研究中，國內外學者主要考慮的結構是熱負荷作用面形狀普遍為方形，且電子元件與散熱器的相對關系大多數局限于圖1所示關系.圖2所示結構是一種應用于大功率整流柜散熱結構，功率器件二極管熱負荷作用面形狀為圓形.對于圖2所示熱負荷作用面為圓形的研究很少.為此，本文將對熱負荷作用面為圓形的電器件散熱器散熱性能進行研究，獲得能快速預測散熱器散熱性能的結果，為此類散熱器的結構優化提供指導.

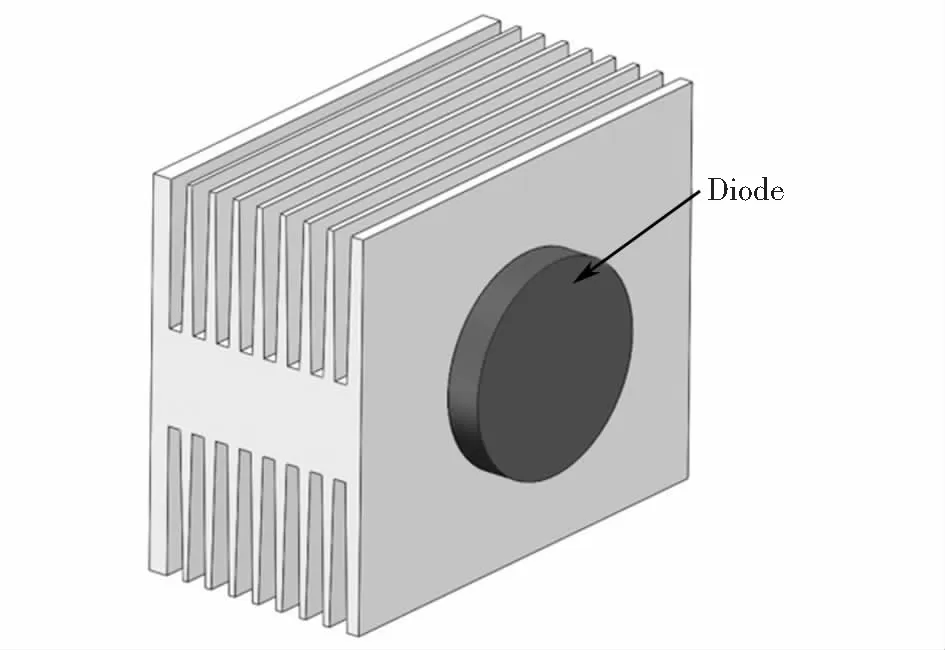
圖2 二極管肋片式散熱器三維簡化模型Fig.2 A three-dimensional simplified model of diode- heated finned structure radiator

1 物理模型

1.1 幾何模型

二極管肋片結構散熱器幾何參數如圖3(a)～(b)所示，為了方便計算，將帶有坡度的肋片厚度t和肋片間距b取平均值，散熱器模型可以看做是由N-1個平行板通道組成.結構參數：翅片數n=9；肋片厚度t(t=3 mm)，肋片間距b(b=5 mm)，肋片高度d(d=46 mm)，肋片長度L(L=140 mm)，肋基厚度S(S=30 mm)，散熱器總高度W(W=71 mm)，總寬度H(H=122 mm).散熱器與二級管相接觸的熱負荷面定義為圓形C面，C面直徑用D表示，在通道氣體進口處指定均勻進口速度U和環境流體溫度Tf.

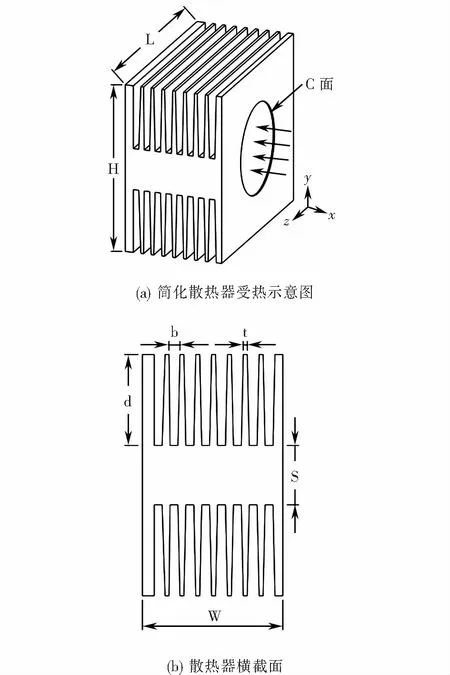
圖3 二極管肋片式散熱器幾何參數Fig.3 Geometric parameters of radiator with diode heating fin structure

1.2 控制方程及邊界條件

散熱器固體區域的導熱微分方程：

(1)

對于強制對流換熱，輻射的熱量比例很小，熱量主要靠空氣對流換熱散發出去，因此，可忽略肋片的輻射換熱，僅考慮其導熱和強制對流換熱.

C面上熱邊界條件

設二極管耗散功率PEH為常數，由導熱第二類邊界條件可得二極管與散熱器接觸面(圓形C面)處的邊界條件為：

(2)

式中:Fc為二極管與肋基接觸位置面積.

除C面以外面上熱邊界條件

(3)

式中:Tw為散熱器壁面溫度，Tf為環境溫度.

1.3 熱阻的定義

(4)

式中:Tmax為散熱器最高溫度.

2 對流換熱系數的確定

要獲得物理模型圖3(a)的熱阻，就得求解方程(1)～(3)，在得到Tmax后就能得到Rf.要求解方程(1)～(3)，先需獲得表面對流傳熱系數h.下面我們介紹一下不求解流動方程獲得該系數的方法.

2.1 邊界層理論估計方法

傳熱學[10]中介紹了經典流體外掠平板層流分析解，雷諾數的定義為：

ReL=UL/ν.

(5)

如果假設肋通道可以用外掠平板近似，則物理模型圖3(a)通道表面的對流傳熱表面傳熱系數近似為：

h=Nu·λ/L.

(6)

式中:L是肋片的全長，U進口風速(m/s)，λ是流體導熱系數，ν流體的運動粘度(m2/s).

2.2 修正邊界層理論直接估計方法

Teertstra[11]等人將圖1形式兩個相同結構的散熱器采取背對背的組合建立了分析模型，對平行平板開口通道中充分發展流動和發展流動兩種極限情況模型分別進行理論求解并得出復合模型解，將肋效率考慮在內，得出了平均努塞爾數與散熱器幾何形狀和流體速度的函數關系以及對強制對流冷卻平板肋片開口通道散熱器的平均換熱率進行了預測.最后在不同的進風速度和發熱功率的情況下對組合散熱器模型進行風洞實驗，將分析模型安裝于緊湊的長方體的玻璃防護罩內以減小旁路效應，分析結果與實驗結果非常吻合，最大誤差為2.1%.

平均對流換熱系數：

h=Nubλ/b.

(7)

平均努塞爾數：

Nub=Nui·η.

(8)

不考慮肋效率時的努塞爾數：

Nui=

(9)

肋效率：

(10)

通道修正雷諾數定義：

(11)

如假設初始環境溫度為40 ℃，在1個大氣壓下干燥空氣的物理參數如表1所示，并對計算進行對比分析.

表1 空氣物性參數

當入口風速U=5 m/s時，ReL=41 273.6小于ReL=5×105層流過渡到湍流的臨界值.因此，入口風速小于5 m/s時，符合流體外掠平板層流解特征數方程適用范圍.進口風速為1 m/s、2 m/s、3 m/s、4 m/s、5 m/s時此類結構散熱器的對流換熱系數h計算結果如圖4所示.

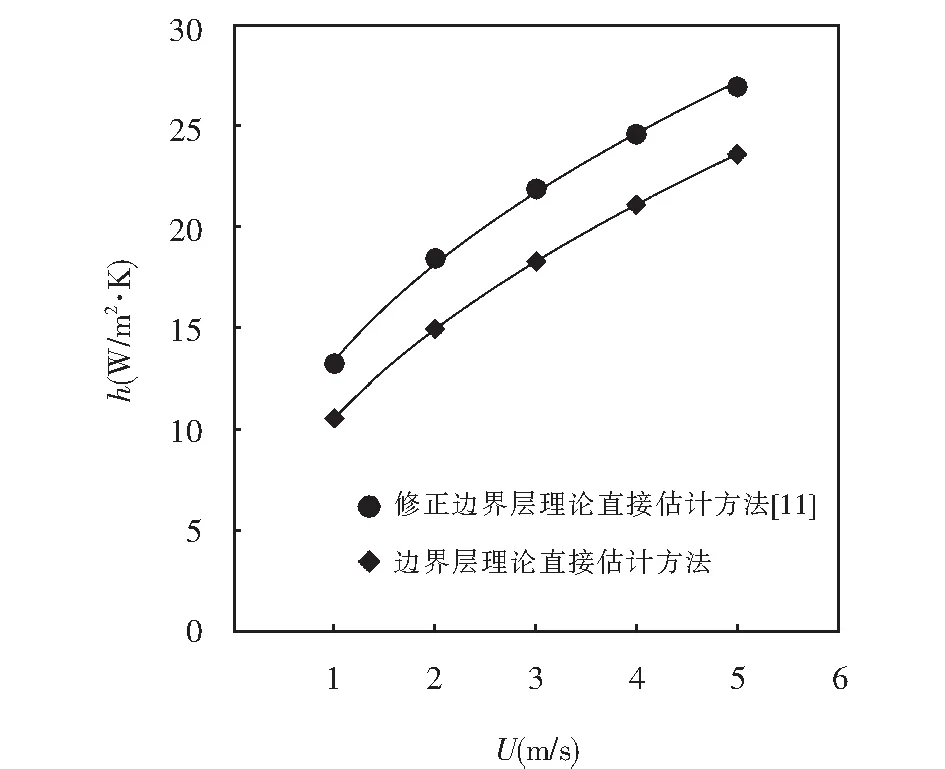
圖4 入口風速對換熱系數的影響Fig.4 Relation between inlet wind speed and heat transfer coefficient

由圖4可以看出，兩種計算方法所得表面傳熱系數變化趨勢一致，最大絕對誤差值為3.5 W/(m·K)，最大相對誤差為16%.由于對流換熱系數的影響因素眾多，散熱器的幾何結構因素是其中之一，將散熱器開口通道結構近似為流體外掠平板進行求解是導致誤差主要的原因.第二種方法針對肋片開口通道結構散熱器，通過理論分析修正與實驗驗證，并且將肋效率考慮在內，比第一種估計方法要準確，從而論文使用第二種方法確定h.

3 數值方法

論文采用FLUENT 17.0軟件進行模型方程(1)～(3)的三維數值模擬計算，為了確保計算結果的精確性，對數值模擬方法進行了網格獨立性考核和可靠性分析.

3.1 網格獨立性考核

網格的劃分方式和類型將對數值模擬的精確解有一定的影響.合適的網格可以更準確地模擬散熱器的熱特性.論文采用多區域方法將整個幾何形狀離散為有限體積的六面體網格[12]，如圖5所示.

圖5 肋片式散熱器計算網格圖Fig.5 Computational grid of a finned radiator

網格單元的數量對數值模擬的結果有很大的影響.為了保證數值計算的準確性，針對數值計算模型采用不同數量的網格進行了網格獨立性考核：論文對加熱功率為500 W，取入口風速U=5 m/s，對流換熱系數值h=26.71 W/m2·K，初始溫度T0=40 ℃，C圓直徑D為66 mm的結構進行了網格獨立性考核，其結果如表2所示.

表2 網格獨立性考核

很明顯所得結果準確性并沒有隨著網格元素數量的顯著增加而顯著提高，這說明使用1.84×106的網格已經能夠獲得網格獨立的結果.

3.2 數值結果驗證

為了確保數值結果的準確性，針對Ong等人[13]對圖1所示結構，熱負荷作用面形狀為方形翅片散熱器所報道的實驗結果，論文采用與實驗件相同結構尺寸的計算模型進行了數值模擬，數值結果與實驗結果的比較如圖6所示.

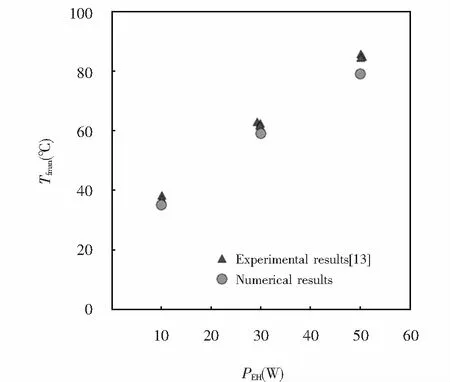
圖6 數值計算結果可靠性驗證Fig.6 Verification of the numerical results reliability

圖6反映了三種輸入功率PEH(10 W、30 W、50 W)的作用下散熱器基板的最大溫度Tfmax實驗結果與數值計算結果.可以看出使用修正換熱系數模擬計算的最大溫度值與實驗值吻合良好.為了提高實驗的準確性，Ong等人在每一個輸入功率PEH下，對實驗重復進行三次，三次試驗結果非常接近.不同功率PEH最大溫度Tfmax的實驗平均值與數值結果的最大相對誤差為6.58%.可見論文中數值方法能獲得可信的結果.

4 結果及分析

4.1 散熱器溫度分布

當散熱器結構參數為n=9，t=3 mm，b=5 mm，d=46 mm，L=140 mm，W=71 mm，H=122 mm，C圓直徑D=66 mm，散熱器材料為鋁，導熱系數λ=202 W/(m·K)，PEH=600 W，U=5 m/s時，熱負荷作用面為圓形二極管散熱器溫度分布如圖7所示.二極管直接作用在散熱器頂板位置，與其他研究文獻中熱源作用在散熱器基板位置不同，因此熱量的傳遞方式也與其他肋片結構散熱器有所不同.二極管產生的熱量由頂板沿肋基和肋高方向逐層進行傳遞，越靠近頂板肋片溫度越高.高溫主要分布在與二極管接觸的頂板肋片表面，最高溫度主要出現在肋基的兩端.如果最高溫度超過器件的節溫，器件失效.因此，掌握該類型結構散熱器溫度分布，對設計者來說，在已知功率器件功率和溫度允許范圍內，對散熱器結構以及數量的選擇有一定的參考意義，使得所選用的散熱器在規定范圍內不容易失效.

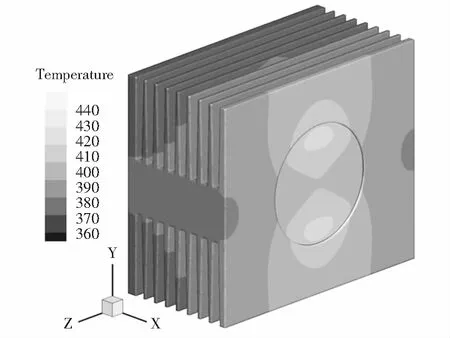
圖7 熱負荷作用面為圓形二極管散熱器溫度分布Fig.7 Temperature distribution of a diode radiator with a circular thermal load acting surface

4.2 Re對熱阻的影響

設定環境溫度為40 ℃，用前述散熱器結構及材質，當二極管輸入功率PEH分別為400 W、500 W、600 W時對不同風速U(即不同雷諾數Re)條件下對散熱器散溫度場進行分析.所得Re和Rf的關系如圖8所示.由圖8可以看出，隨著Re的不斷增大，三組不同輸入功率PEH作用下的熱阻Rf曲線走勢一致，均以一定的規律逐漸減小，Re相同時，不同的輸入功率PEH，熱阻Rf值相等.

4.3 散熱器材質導熱系數對熱阻的影響

設定環境溫度為40 ℃，U=5 m/s，二極管輸入功率PEH分別為400 W、500 W、600 W，散熱器結構參數同前述，用不同材質的散熱器進行溫度場分析.所得導熱系數λ和Rf的關系如圖9所示.可以看出，散熱器的熱阻Rf隨著材料導熱系數的增大逐漸減小.

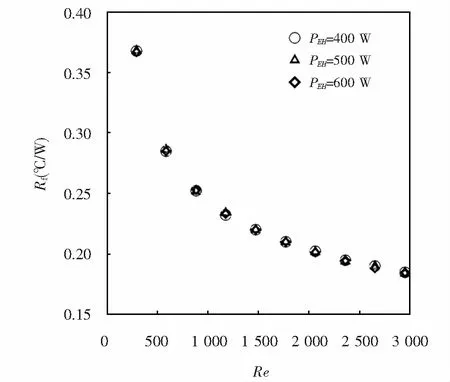
圖8 雷諾數Re對熱阻的影響Fig.8 Influence of Reynolds number on thermal resistance

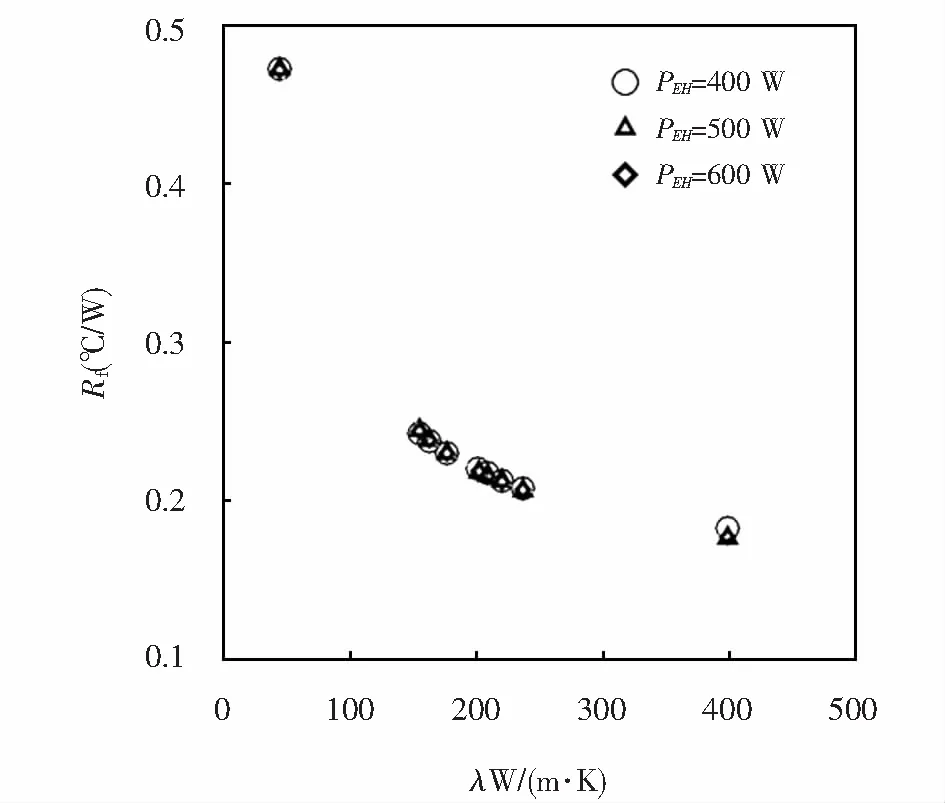
圖9 導熱系數λ對熱阻的影響Fig.9 Influence of thermal conductivity on thermal resistance

4.4 熱負荷作用面直徑D對熱阻的影響

散熱器結構參數同前述，當二極管輸入功率PEH分別為400 W、500 W、600 W，空氣速度U=5 m/s(Re=1 474)，改變熱負荷作用C面直徑D的尺寸對該結構散熱器散熱溫度場分析，所得熱阻如圖10所示.可以看出，三種不同輸入功率PEH作用下，隨著熱負荷作用C面直徑D的增大，散熱器熱阻的變化趨勢基本一致.當熱負荷作用C面的直徑D增加時，散熱器熱阻逐漸減小并趨于穩定，但隨著C面直徑D繼續增加，熱阻又不斷增大.當C面直徑D等于60 mm左右，熱阻值達到最小.說明當熱源通過熱傳導的形式將熱量傳遞給散熱器時，需要考慮熱源與散熱器的接觸面積，接觸面積大小不同時會導致導熱熱阻的變化.

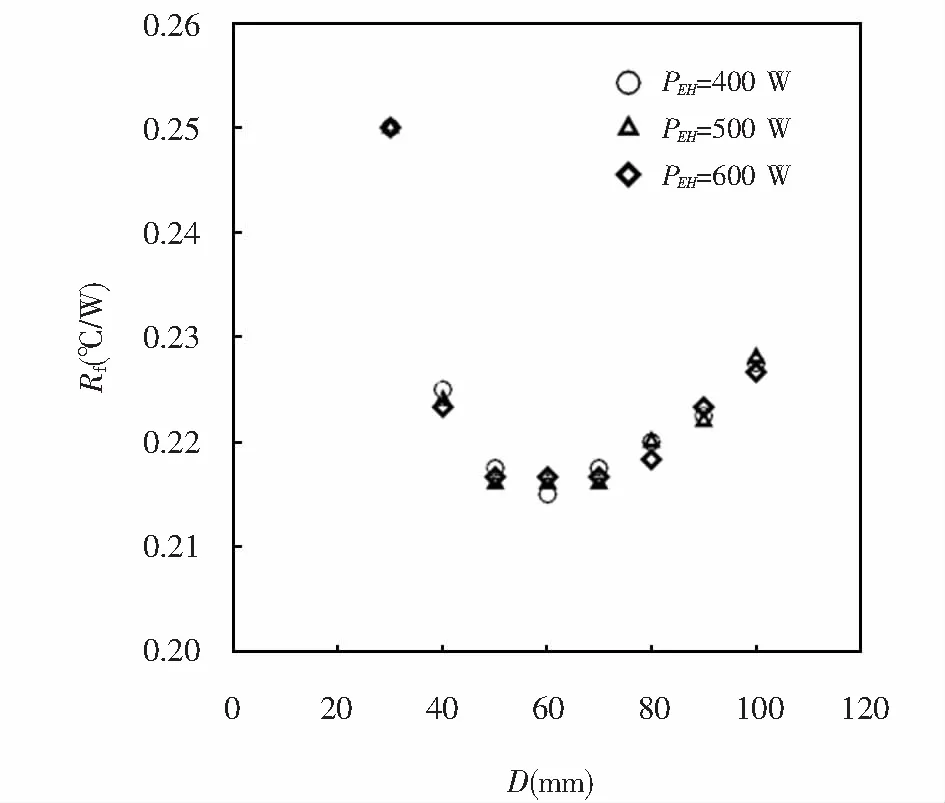
圖10 熱負荷作用C面直徑D對熱阻的影響Fig.10 Influence of thermal load surface diameter D on thermal resistance

圖1所示為常見的散熱器結構，其熱量傳遞方向只沿著肋高方向傳遞.文獻[14]中對這一結構散熱器接觸面積對熱阻的影響進行了研究，得出結論：熱負荷作用面面積與肋片基板面積相等時熱阻值最小.然而本文所研究的散熱器結構熱負荷作用在肋片基板的一側(作用在肋片頂板)，熱量的傳遞方向是先從頂板開始傳遞，同時沿著肋基方向，再沿著肋高方向進行傳遞.熱負荷作用C面面積的大小除了和肋片頂板面積有關之外，更多的和肋基的厚度S有關.計算可得，對于論文中這一結構類型的散熱器，肋基的厚度S與熱負荷作用C面的直徑D的比值等于0.5，即S/D=0.5時，熱量可有效的沿肋基和肋高方向傳遞進行散熱，熱阻值達到最小.

4.5 熱負荷對熱阻的影響

圖8～10表明，C面上加熱功率PEH與熱阻關聯度不大.這主要是在計算Nu時用了固定的特征溫度即初始環境溫度都設定為40 ℃.因此，在散熱器結構參數固定不變的情況下，由式(9)～(13)可得其Nu保持不變.當加熱功率PEH增大時，使得最大溫度Tmax相應增大，但不改變其熱阻的大小.在后續的設計計算中，可忽略熱負荷作用面上加熱功率PEH對熱阻的影響.

5 結論

論文通過理論和數值方法分析了熱負荷作用面為圓形電器件散熱器散熱特性，并且在已知散熱器尺寸參數和來流風速的情況下，能夠快速容易的預測散熱器的對流傳熱系數、肋效率、表面溫度分布以及散熱器熱阻.與大多數文獻研究的熱負荷作用面形狀為方形的翅片散熱器散熱性能有所不同，本文中發熱器件熱負荷作用面形狀為圓形，熱量的傳遞方式由肋片頂板沿肋基和肋高方向逐層傳遞，而大多數文獻中熱量的傳遞是由基板傳向肋高方向.論文結論可總結如下：

1) 求解工程對流傳熱問題時，對設計者而言，在選用類似肋片結構散熱器時，根據Teertstra提出的試驗關聯式能夠快速預測估計其散熱效率和表面傳熱系數.

2) 熱負荷作用面形狀為圓形時，最高溫度分布出現在加熱區域肋基的兩端.

3) 熱阻Rf隨著雷諾數Re和材料的導熱系數λ增大而減小，熱阻Rf與雷諾數Re存在唯一對應關系.

4) 熱阻隨著熱負荷作用C面直徑D的增加呈現先減小后增加的變化規律.研究表明，熱負荷作用C面面積大小對導熱熱阻有較大影響.論文中的散熱器結構，當肋基的厚度S與熱負荷作用C面的直徑D的比值等于0.5時，熱量從頂板有效的沿肋基和肋高方向傳遞進行散熱，熱阻值達到最小.