一種NPC三電平逆變器驅(qū)動PMSM的FCS-MPTC改進(jìn)策略

劉川澤，李彥哲，郭小嘉

(蘭州交通大學(xué) 自動化與電氣工程學(xué)院，蘭州 730070)

相比于傳統(tǒng)兩相拓?fù)浣Y(jié)構(gòu)，中點(diǎn)鉗位型(neutral point clamped,NPC)三電平逆變器具有單個開關(guān)元所承受的電壓應(yīng)力低、輸出電流總諧波失真值小和控制自由度高等優(yōu)點(diǎn)，適用于各種高壓大功率領(lǐng)域[1].但NPC由于電容充、放電時間不同，存在母線電容中點(diǎn)電壓波動的問題，影響系統(tǒng)運(yùn)行的可靠性[2-3].

直接轉(zhuǎn)矩控制(direct torque control,DTC)作為主流高性能的永磁同步電機(jī)(permanent magnet synchronous motor,PMSM)控制算法，在過去幾十年一直是國內(nèi)外學(xué)者關(guān)注的熱點(diǎn)[4-5].然而傳統(tǒng)DTC算法存在穩(wěn)態(tài)性能差和轉(zhuǎn)矩脈動大等固有問題，將NPC逆變器應(yīng)用于DTC算法，由于不同扇區(qū)的電壓矢量往往不能直接切換，需要采用插入過渡電壓的方法來滿足逆變器運(yùn)行需求，由于過渡電壓與磁鏈和轉(zhuǎn)矩相互影響，存在不穩(wěn)定因素，經(jīng)常導(dǎo)致系統(tǒng)控制效果不佳，甚至放大DTC算法的缺點(diǎn)[6-7].近年來，有學(xué)者提出有限集模型預(yù)測轉(zhuǎn)矩控制(finite control set model predictive torque control,FCS-MPTC)算法，因其電磁轉(zhuǎn)矩脈動小和定子電流諧波含量小等優(yōu)點(diǎn)受到廣泛關(guān)注[8].

將FCS-MPTC應(yīng)用于NPC三電平逆變器驅(qū)動PMSM的控制系統(tǒng)，只需根據(jù)切換電壓的要求實(shí)時選擇電壓控制集并預(yù)測中點(diǎn)電壓，通過目標(biāo)函數(shù)增加中點(diǎn)電位控制項，即可實(shí)現(xiàn)中點(diǎn)電壓平衡[9-10]，滿足NPC三電平逆變器的運(yùn)行要求.其缺點(diǎn)是FCS-MPTC算法的運(yùn)算復(fù)雜度隨著電平數(shù)的增加將會呈指數(shù)式爆炸增長，增加了系統(tǒng)的運(yùn)行負(fù)擔(dān)，雖然可以采用延長控制周期的方法進(jìn)行解決，但是由于控制算法開關(guān)頻率的減少，無法抑制較大的轉(zhuǎn)矩脈動[11].文獻(xiàn)[12-13]利用伏秒平衡原理，選擇相鄰矢量按照特定占空比合成有效虛擬電壓矢量得到參考電壓，抑制了輸出電流的低次諧波分量并簡化了算法，但使用合成矢量降低了電壓利用率.

基于此，以三相表貼式PMSM為對象，針對NPC三電平逆變器驅(qū)動系統(tǒng)，采用一種無差拍算法與扇區(qū)細(xì)分方法結(jié)合的電壓矢量優(yōu)化選取策略，以降低FCS-MPTC算法的運(yùn)算量;針對三電平預(yù)測控制中點(diǎn)電壓不平衡問題，構(gòu)建考慮中點(diǎn)電壓均衡問題的目標(biāo)函數(shù)，以實(shí)現(xiàn)中點(diǎn)電壓平衡控制；以誤差率評估代替?zhèn)鹘y(tǒng)的磁鏈和轉(zhuǎn)矩誤差評估，消除權(quán)重系數(shù)，并考慮定子電流限幅問題，最終實(shí)現(xiàn)FCS-MPTC算法的優(yōu)化改進(jìn).

1 NPC三電平逆變器拓?fù)渑cPMSM數(shù)學(xué)模型

1.1 NPC三電平逆變器的拓?fù)浣Y(jié)構(gòu)

NPC型三電平逆變器拓?fù)浣Y(jié)構(gòu)如1所示.

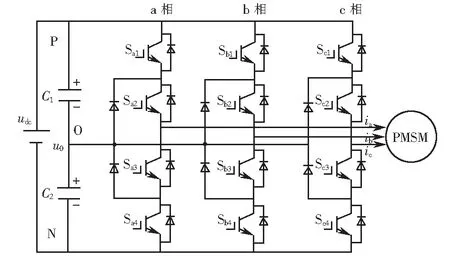
圖1 NPC型三電平逆變器容錯拓?fù)銯ig.1 NPC three-level inverter fault-tolerant topology

每相輸出三種電壓分別為udc/2、0和-udc/2.P代表著連接至母線的正端，O代表著連接至相關(guān)直流側(cè)對應(yīng)的中點(diǎn)，N代表連接到相關(guān)的負(fù)端.

對于NPC三電平逆變裝置，其空間電壓矢量分布區(qū)域如圖2所示.

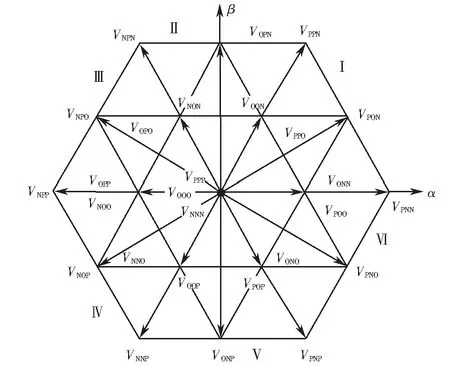
圖2 三電平逆變器的開關(guān)狀態(tài)和空間電壓矢量Fig.2 Switching state and space voltage vector of three- level inverter

1.2 PMSM數(shù)學(xué)模型

本文將表貼式PMSM視作控制對象，將鐵心損耗、阻尼繞組忽略.于是就能得到PMSM在兩相靜止坐標(biāo)系中，相應(yīng)的定子電流與磁鏈方程[14]，依次為：

(1)

(2)

式中：iα和iβ分別為α-β軸電流分量；Ls為定子電感；Rs為定子電阻；ψf為永磁體磁鏈幅值；ωe為轉(zhuǎn)子電角速度；θe為轉(zhuǎn)子位置角；uα和uβ分別為α-β軸電壓分量；ψα和ψβ分別為α-β軸磁鏈分量.

定子磁鏈和電磁轉(zhuǎn)矩表達(dá)式分別為：

(3)

Te=1.5p(ψαiβ-iαψβ).

(4)

式中:ψs和Te分別為定子磁鏈和電磁轉(zhuǎn)矩；p為電機(jī)極對數(shù).

2 PMSM模型預(yù)測控制

2.1 傳統(tǒng)FCS-MPTC

利用歐拉公式對式(1)～(2)進(jìn)行離散得到離散的電流方程和磁鏈方程：

(5)

(6)

式中：Ts為系統(tǒng)采樣時間；k為當(dāng)前采樣時刻；k+1為預(yù)測時刻.

根據(jù)式(5)～(6)可以得到(k+1)Ts時間內(nèi)的定子磁鏈和電磁轉(zhuǎn)矩預(yù)測值為：

(7)

(8)

由此可見，傳統(tǒng)FCS-MPTC根據(jù)當(dāng)前時刻電流、電壓和電角速度預(yù)測下一時刻電流.在其基礎(chǔ)上，將各電壓矢量依次代入電磁轉(zhuǎn)矩和定子磁鏈預(yù)測方程，對各矢量作用下的轉(zhuǎn)矩和磁鏈進(jìn)行預(yù)測.

2.2 改進(jìn)的FCS-MPTC

因為三電平逆變器可以提供的基本電壓矢量為27個，傳統(tǒng)FCS-MPTC需要在單個周期內(nèi)借助枚取的27個開關(guān)狀態(tài)得到該預(yù)測模型的滾動優(yōu)選來獲取所需最佳電壓矢量，會造成很大處理器計算負(fù)擔(dān).對于無差拍控制而言，可以按照磁鏈誤差、轉(zhuǎn)矩來對k時間節(jié)點(diǎn)下的電壓矢量直接進(jìn)行計算[15].

忽略定子電阻壓降，施加電壓矢量所引起的定子磁鏈變化如圖3所示.

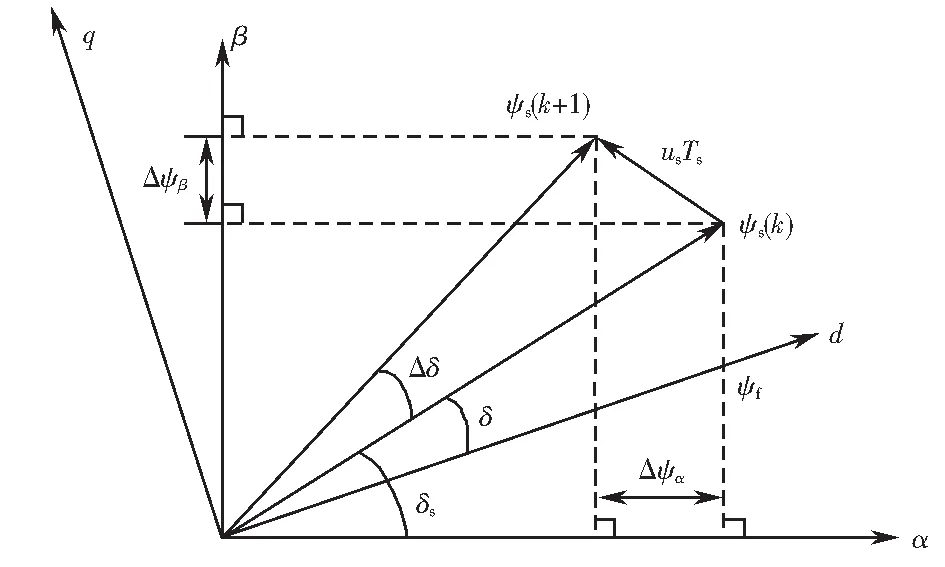
圖3 各參量之間關(guān)系Fig.3 Relationship between the parameters

三相PMSM電磁轉(zhuǎn)矩方程為

(9)

式中，δ為轉(zhuǎn)矩角.

在Ts控制周期內(nèi)，電機(jī)機(jī)械時間常數(shù)要遠(yuǎn)遠(yuǎn)比電氣時間常數(shù)大，轉(zhuǎn)子位置通常有極小的變動，所以可近似認(rèn)為

sinδ≈δ.

(10)

根據(jù)一個控制周期內(nèi)的轉(zhuǎn)矩差值可計算出所需轉(zhuǎn)矩角的變化量Δδ(k)為

(11)

根據(jù)式(11)及圖3所示的空間關(guān)系可以得到一個采樣周期的定子磁鏈誤差為：

(12)

式中：Δψα和Δψβ分別為α-β軸定子磁鏈誤差分量；δs為k時刻定子磁鏈與α軸夾角.

(13)

根據(jù)式(13)可以直接計算出下一時刻需要的電壓矢量，并以此作為當(dāng)前采樣時刻的參考電壓.

2.3 扇區(qū)判斷和最優(yōu)電壓矢量選擇

通過改進(jìn)的FCS-MPTC可以直接計算出下下一時刻的電壓矢量，但是FCS-MPTC基本電壓矢量的選擇依然需要對27個基本電壓矢量進(jìn)行遍歷選取.為了進(jìn)一步減小計算量，可以先對NPC逆變器提供的空間矢量扇區(qū)進(jìn)行預(yù)判.

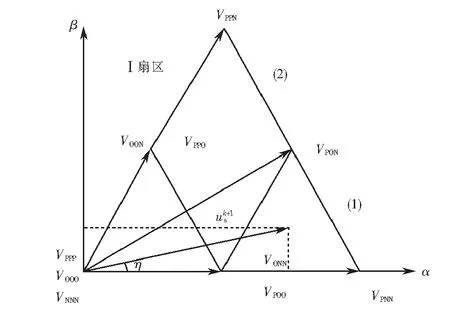
圖4 Ⅰ扇區(qū)各參量之間關(guān)系Fig.4 Relationship between parameters of sector Ⅰ

圖4中，η為電壓矢量與α軸的夾角，根據(jù)相位角η和扇區(qū)分布，可以確定電壓矢量所對應(yīng)的扇區(qū)，這樣就可得到該扇區(qū)的零和非零矢量，并將這些矢量作為待選矢量.將Ⅰ扇區(qū)分為(1)和(2)兩個扇區(qū)，相應(yīng)的其他扇區(qū)采用相同的細(xì)分方法，則總共分為(1)～(12)共12個扇區(qū).

2.4 考慮中點(diǎn)電壓平衡的目標(biāo)函數(shù)優(yōu)化設(shè)計

NPC三電平逆變器相較于傳統(tǒng)兩電平拓?fù)涮峁┝烁嗟碾妷菏噶浚@樣相應(yīng)的諧波含量會隨之下降.然而三電平逆變器存在中點(diǎn)電壓波動的問題.

中點(diǎn)電流不為零是中點(diǎn)電壓波動的本質(zhì)原因.中點(diǎn)電壓u0與三相電流的關(guān)系為[16]

(14)

式中：u0為中點(diǎn)電壓；|Sabc|=[|sa| |sb| |sc|]T為開關(guān)狀態(tài)組合；iabc=[iaibic]T為三相電流；C為直流測電容.

采用歐拉法對式(14)進(jìn)行離散化，可以得到NPC三電平逆變器中點(diǎn)電壓的預(yù)測模型，在目標(biāo)函數(shù)中增加對NPC逆變器中點(diǎn)電壓偏差的約束，可以實(shí)現(xiàn)三電平逆變器中點(diǎn)電壓的預(yù)測控制.

由式(14)可得中點(diǎn)電壓u0在k+1時刻的預(yù)測值為

(15)

同時，在目標(biāo)函數(shù)的設(shè)計中考慮以下兩點(diǎn)問題：

1) 改進(jìn)FCS-MPTC做了一定程度的近似處理，采用均方根差的方法得到更準(zhǔn)確的誤差對其進(jìn)行一定程度的補(bǔ)償，并將電磁轉(zhuǎn)矩和定子磁鏈的誤差改進(jìn)為相對應(yīng)的誤差率的方法，將參量處理為同一量綱，避免了權(quán)重系數(shù)的整定；

2) 考慮定子電流限幅的問題，使定子電流不至于過大，保證控制系統(tǒng)更加安全穩(wěn)定.

根據(jù)式(15)得到的中點(diǎn)電壓預(yù)測值，并將以上兩點(diǎn)期望考慮在內(nèi)的FCS-MPTC目標(biāo)函數(shù)設(shè)計為[17]

(16)

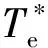
(17)

式中，imax為最大允許定子電流幅值.

2.5 系統(tǒng)延遲補(bǔ)償問題

考慮實(shí)際數(shù)控系統(tǒng)，輸出參量與給定值往往存在相應(yīng)的延遲，為了避免FCS-MPTC受到該延遲的影響，可以引入一個節(jié)拍來對該延時進(jìn)行補(bǔ)償.具體目標(biāo)函數(shù)為

(18)

3 仿真研究

3.1 改進(jìn)系統(tǒng)結(jié)構(gòu)框圖

本文設(shè)計的系統(tǒng)結(jié)構(gòu)框圖如圖5所示，圖中3s/2s表示三相到兩相坐標(biāo)變換.

為了驗證所設(shè)計方案的有效性,本文以Matlab/Simulink為平臺進(jìn)行仿真研究.所用PMSM電機(jī)參數(shù)見表1.

3.2 改進(jìn)系統(tǒng)對比仿真分析

為了驗證所提改進(jìn)FCS-MPTC策略的有效性和優(yōu)越性，將改進(jìn)策略與傳統(tǒng)FCS-MPTC進(jìn)行對比分析，兩套系統(tǒng)采用完全相同的電機(jī)參數(shù)，而傳統(tǒng)FCS-MPTC逆變器采用傳統(tǒng)兩相逆變器.

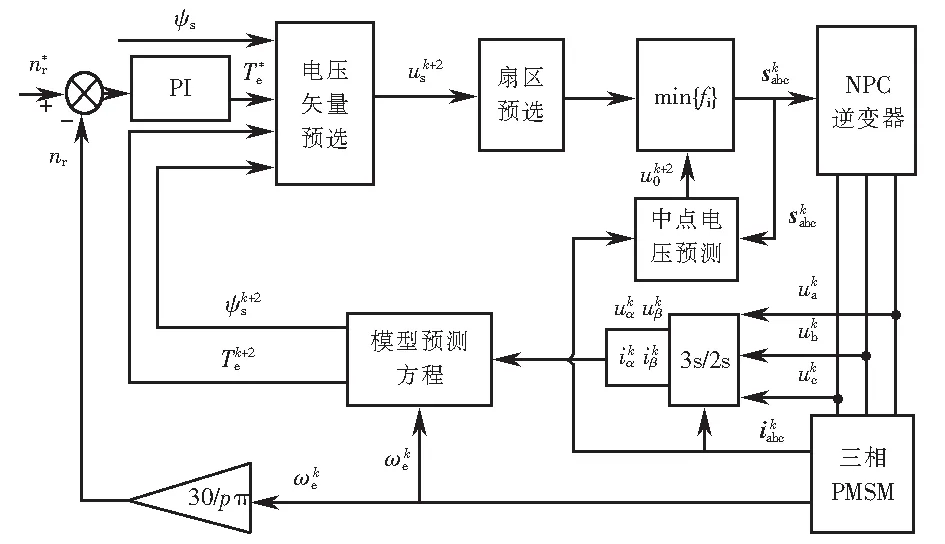
圖5 系統(tǒng)結(jié)構(gòu)框圖 Fig.5 System structure block diagram

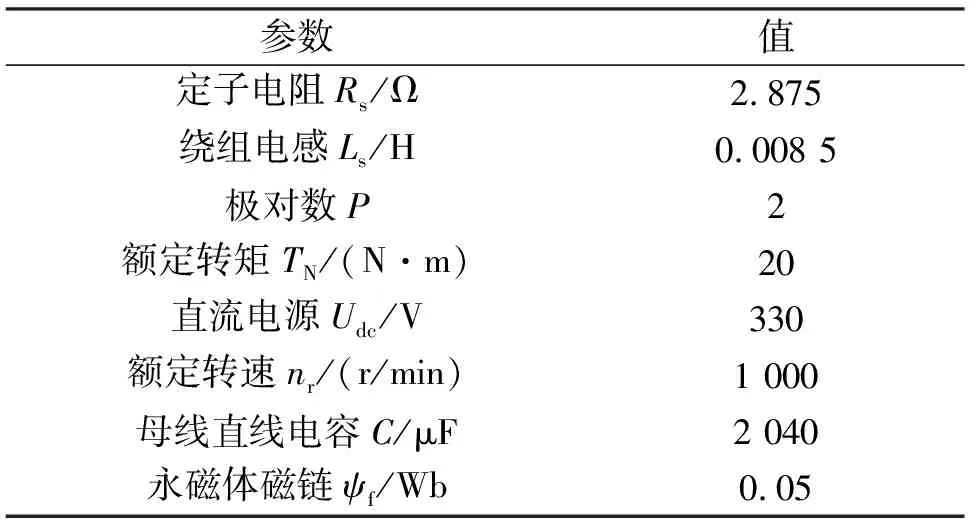
表1 電機(jī)參數(shù)

首先驗證所提策略的中點(diǎn)電壓控制效果.圖6為電機(jī)空載運(yùn)行在1 000 r/min下的中點(diǎn)電壓u0的仿真曲線.系統(tǒng)運(yùn)行至0.2 s，在目標(biāo)函數(shù)中加入母線中點(diǎn)電壓控制，可以看出，0.2 s前u0大幅偏離0 V位置，考慮到逆變器電源為300 V，u0波動最大值達(dá)到了50%，這對于系統(tǒng)是非常不安全的，0.2 s加入中點(diǎn)電壓控制之后，u0穩(wěn)定在零值左右，明顯提高了系統(tǒng)控制性能.

圖6 中點(diǎn)電壓波動曲線Fig.6 Midpoint voltage fluctuation curve

其次，比較兩種策略在負(fù)載突變時的控制效果.兩部電機(jī)均以給定轉(zhuǎn)速為1 000 r/min的情況下空載啟動，在0.2 s時突加1.5 N·m的負(fù)載，各系統(tǒng)轉(zhuǎn)速響應(yīng)如圖7～8所示.可見采用改進(jìn)策略的系統(tǒng)在負(fù)載突變時轉(zhuǎn)速小幅下降后立刻恢復(fù)到穩(wěn)定運(yùn)行狀態(tài)，而采用傳統(tǒng)策略的系統(tǒng)轉(zhuǎn)速降幅和恢復(fù)時間均約為改進(jìn)策略的1.5倍，體現(xiàn)了所提策略應(yīng)對負(fù)載變化良好的魯棒性.

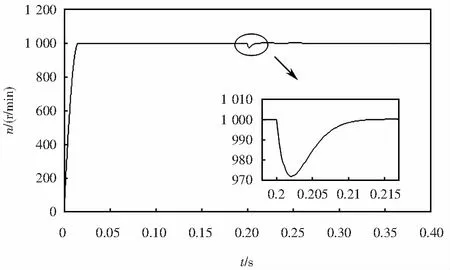
圖7 傳統(tǒng)FCS-MPTC轉(zhuǎn)速響應(yīng)Fig.7 Traditional FCS-MPTC speed response

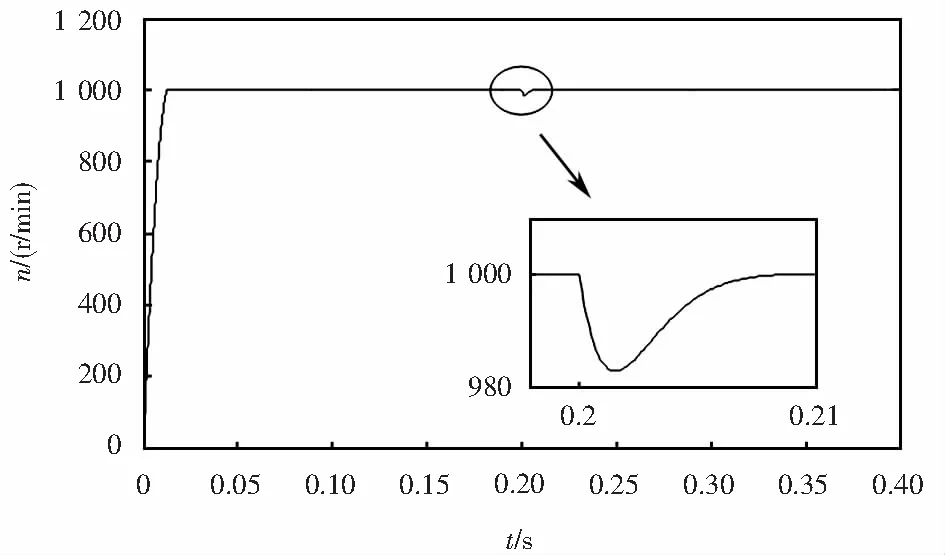
圖8 改進(jìn)FCS-MPTC轉(zhuǎn)速響應(yīng)Fig.8 Improved FCS-MPTC speed response

圖9～10為兩套系統(tǒng)磁鏈幅值變化曲線.可以看出采用改進(jìn)策略的系統(tǒng)磁鏈幅值在負(fù)載突變前后基本保持為給定值，且?guī)谉o波動，而采用傳統(tǒng)策略的系統(tǒng)磁鏈幅值在負(fù)載突變后有明顯上升，且波動幅值較大.

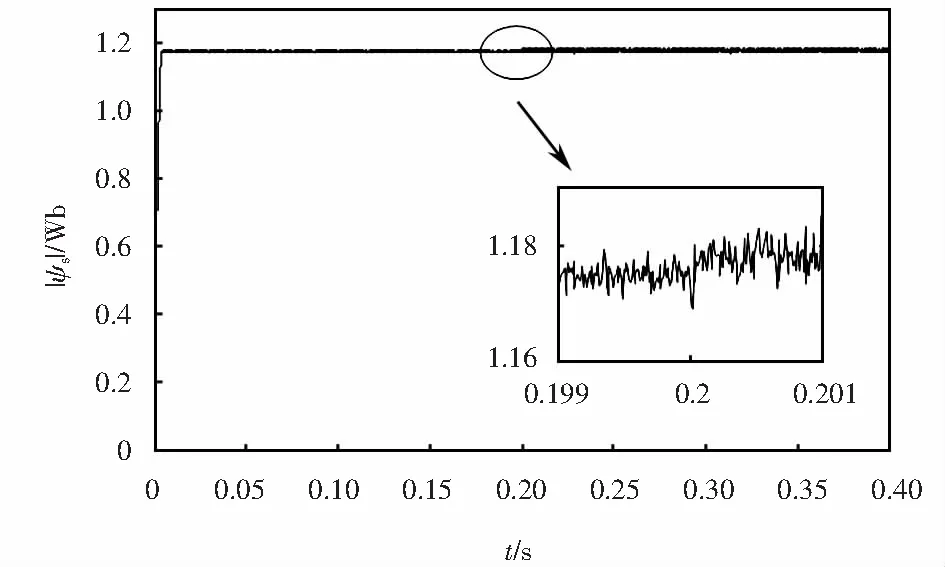
圖9 傳統(tǒng)FCS-MPTC磁鏈幅值變化曲線Fig.9 Traditional FCS-MPTC flux link amplitude change curve

圖11～12為兩套系統(tǒng)的電磁轉(zhuǎn)矩響應(yīng)曲線.可以看出，采用改進(jìn)策略的系統(tǒng)電磁轉(zhuǎn)矩脈動明顯小于采用傳統(tǒng)策略的系統(tǒng)，這對于系統(tǒng)的穩(wěn)定運(yùn)行和節(jié)能問題有重要意義.

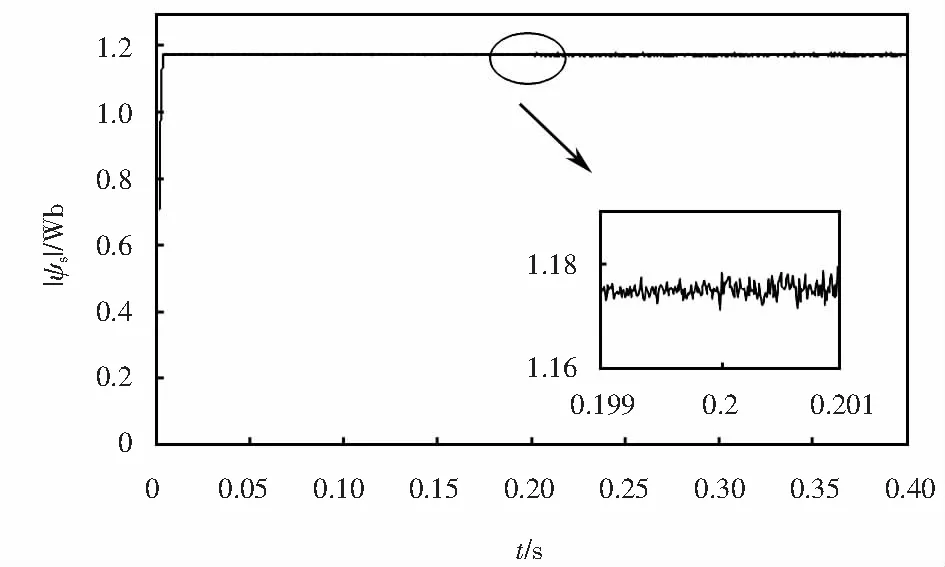
圖10 改進(jìn)FCS-MPTC磁鏈幅值變化曲線Fig.10 Improved FCS-MPTC flux linkage amplitude change curve

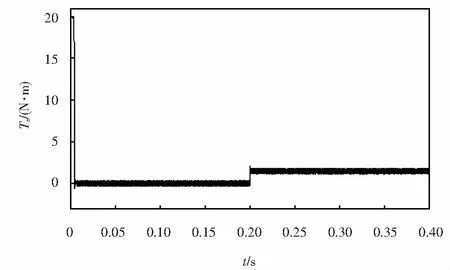
圖11 傳統(tǒng)FCS-MPTC電磁轉(zhuǎn)矩響應(yīng)Fig.11 Traditional FCS-MPTC electromagnetic torque response

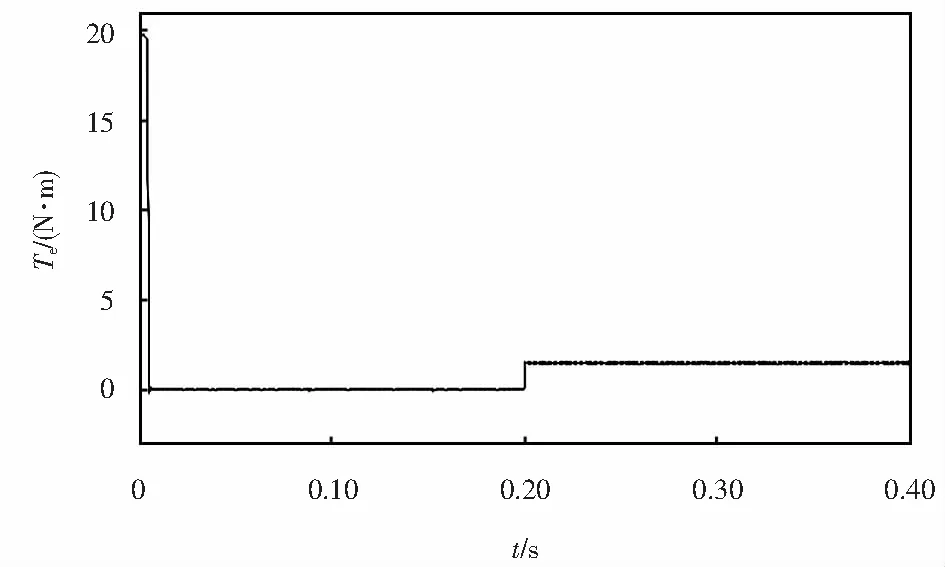
圖12 改進(jìn)FCS-MPTC電磁轉(zhuǎn)矩響應(yīng)Fig.12 Improved FCS-MPTC electromagnetic torque response

圖13～14為兩套控制系統(tǒng)的磁鏈響應(yīng)，可以看出，相較于傳統(tǒng)的FCS-MPTC，通過對其優(yōu)化改進(jìn)，可以將定子磁鏈軌跡與圓形更為相近，相應(yīng)的磁鏈脈動也顯著下降，穩(wěn)定性得到了明顯增長.

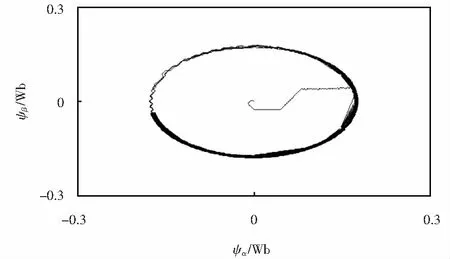
圖13 傳統(tǒng)FCS-MPTC定子磁鏈軌跡Fig.13 Traditional FCS-MPTC stator flux trajectory

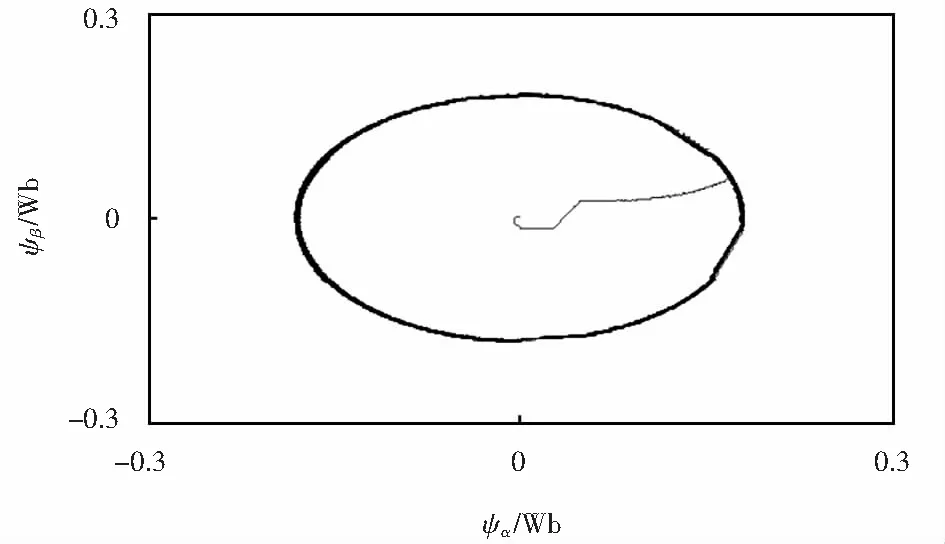
圖14 改進(jìn)FCS-MPTC定子磁鏈軌跡Fig.14 Improved FCS-MPTC stator flux trajectory

圖15～16為兩套系統(tǒng)定子電流響應(yīng)，可以看出，相比于傳統(tǒng)FCS-MPTC算法，改進(jìn)的系統(tǒng)輸出定子電流波形更加穩(wěn)定平滑.由圖15～16進(jìn)行THD分析可知，采用改進(jìn)策略的系統(tǒng)三相定子電流THD均值為7.87%，而采用傳統(tǒng)策略的系統(tǒng)三相定子電流THD均值為13.24%，由此亦說明了NPC三電平逆變器因可提供更多電壓矢量，而呈現(xiàn)出更為精細(xì)的電壓控制效果.

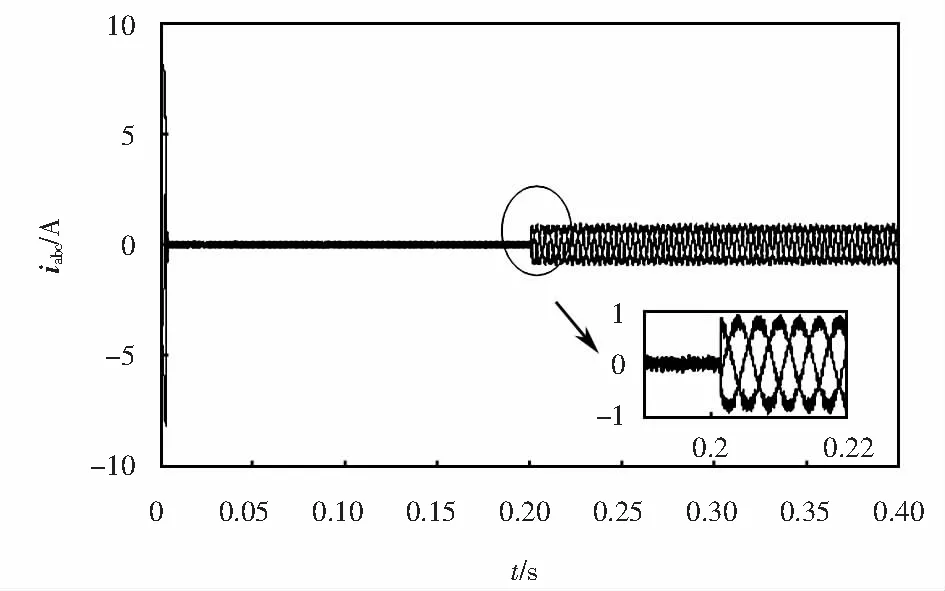
圖15 傳統(tǒng)FCS-MPTC定子電流Fig.15 Traditional FCS-MPTC stator current

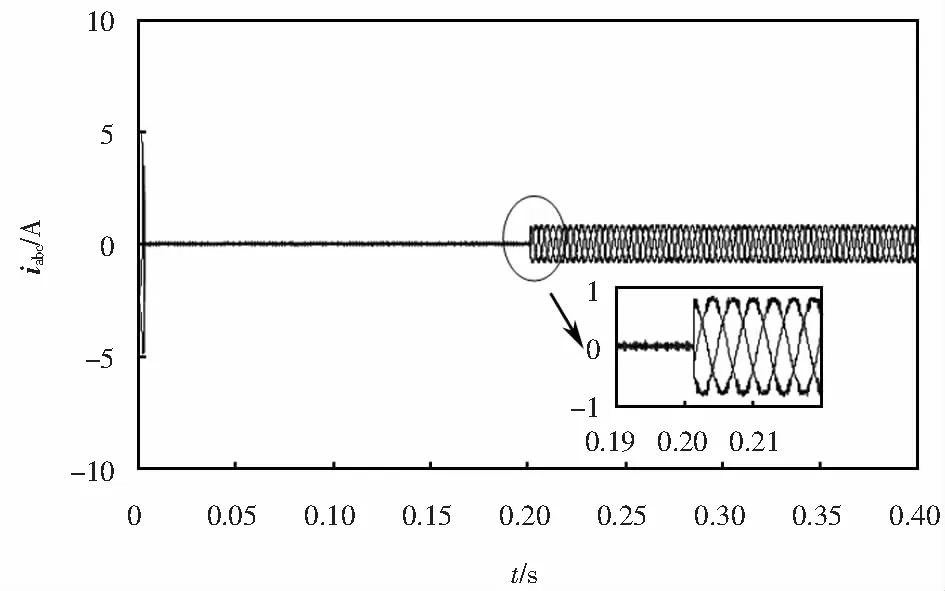
圖16 改進(jìn)FCS-MPTC定子電流Fig.16 Improved FCS-MPTC stator current

4 結(jié)論

本文針對NPC三電平逆變器驅(qū)動的PMSM系統(tǒng)，提出了一種無差拍算法與扇區(qū)細(xì)分判斷方法結(jié)合的電壓矢量優(yōu)化選取策略.與傳統(tǒng)FCS-MPTC算法相比，所設(shè)計的FCS-MPTC改進(jìn)策略能夠?qū)崿F(xiàn)中點(diǎn)電壓平衡控制，有效降低了運(yùn)算量，并使得轉(zhuǎn)矩與磁鏈脈動更小，定子電流諧波失真值降低，具有良好的動靜態(tài)性能.仿真結(jié)果驗證了改進(jìn)策略的可行性和有效性.