不同理論在分析箱形梁畸變效應時的差異

王晨光，張元海

(蘭州交通大學 土木工程學院，蘭州 730070)

高強、薄壁、輕型化是箱形梁橋未來發展的趨勢.薄壁箱梁在偏心荷載作用下的畸變效應顯著，在橋梁設計過程中必須引起足夠重視[1-8].張元海等[9]給出了箱形截面畸變角的一般定義，并提出了一種類似于箱梁約束扭轉分析的畸變效應解析法來分析布置雙層懸臂板箱梁的畸變效應.徐勛等[10]基于廣義坐標法建立位移模式和幾何方程，采用混合變分原理，建立了開閉口混合截面薄壁桿件扭轉和畸變分析理論，以充分考慮剪切變形對箱形梁畸變效應的影響.王兆南等[11]采用板元分析法，通過建立各板元面內矩、相互約束及畸變荷載之間的關系，推導了箱形梁畸變控制微分方程.張文獻等[12]對長懸臂板箱形梁的畸變效應進行了模型試驗研究，通過對實測數據進行回歸分析，得到長懸臂板箱形梁畸變橫向彎矩的實用計算公式.Chidolue等[13]基于符拉索夫廣義坐標法的基本原理求解得到了三室全斜腹板箱梁的畸變控制微分方程，并通過三角級數法計算箱形梁的畸變變形.朱力等[14]通過虛功原理構造了曲線梁的平衡方程,給出了曲梁的剛度矩陣及等效荷載矩陣.張莉[15]通過有限元軟件分析了橫隔板的數量及箱梁的幾何特征參數對鋼箱梁畸變效應的影響.畸變分析理論眾多，不同畸變理論在分析箱形梁畸變效應時既有區別又有聯系.本文通過對板元分析法、能量分析法這兩種不同畸變理論進行比較，進一步探討了兩種理論之間的關系.

1 畸變荷載及畸變變形

在分析箱形梁畸變效應時，可沿箱梁跨度方向截取單位長度的薄片框架，其橫截面簡圖如圖1所示.圖中，A、B、C、D分別為箱室的四個角點.bw、bt、bd分別為箱室腹板、頂板、底板的長度；bf為翼緣板長度；δt、δw、δd分別為頂板、腹板、底板的厚度.θ為頂板與腹板的夾角.偏心荷載P(z)作用在頂板上，偏心距為e.

作用在箱形梁橫截面上的偏心荷載可以分解為正對稱荷載和反對稱荷載，其中反對稱荷載可以繼續分解為剛性扭轉荷載和畸變荷載.正對稱荷載和剛性扭轉荷載不引起箱形梁的畸變變形，在分析箱形梁畸變效應時往往可以忽略.根據畸變荷載的自平衡條件，可得作用在箱形梁橫截面上的畸變荷載如圖2所示，其值分別為

(1)

(2)

(3)

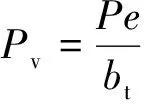
圖1 箱形梁橫截面簡圖Fig.1 Diagram of cross section of box girder

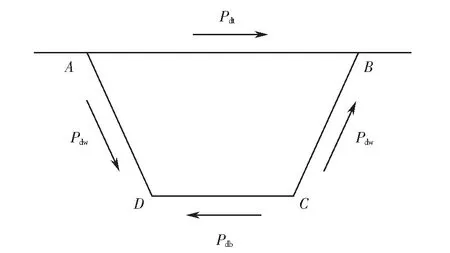
圖2 畸變荷載Fig.2 Distortion Loads

組成箱形梁的各板件在畸變荷載作用下發生了平面內翹曲變形和平面外框架變形，分別如圖3～4所示.定義角點D處腹板與底板夾角的改變量為γD，如圖4所示，則這兩種變形最終可以通過畸變角γD聯系起來.

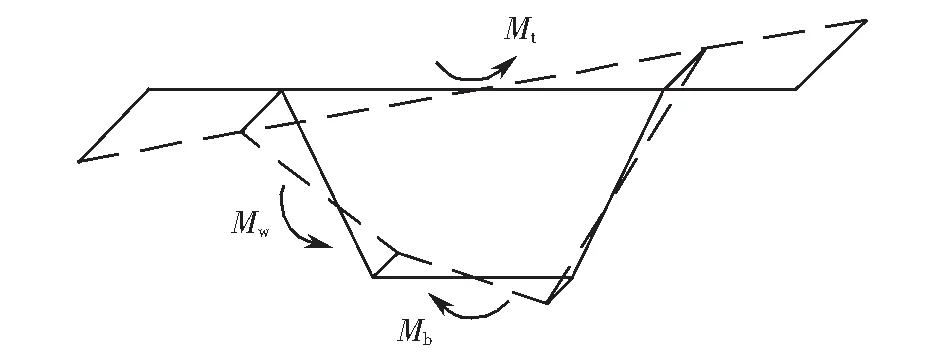
圖3 平面內畸變翹曲變形Fig.3 In-plane deformation due to distortion warping

在分析畸變翹曲變形時，認為組成箱形梁各板件在發生畸變翹曲時滿足平截面假定，此時，各板件平面內的位移滿足初等梁理論，畸變翹曲正應力呈線性分布.由畸變翹曲正應力的自平衡條件可得，頂板、底版、腹板上由畸變翹曲正應力合成的內力矩Mt、Mb、Mw滿足以下條件

(4)

(5)

(6)

式中：E為彈性模量.

圖4 平面外畸變框架變形Fig.4 Out-plane distortion deformation of the frame

當箱形梁框架產生畸變角γD時，頂板水平位移為γDbwsinθ，如圖4所示.通過計算可以得到箱形梁在發生畸變框架變形時角點A、角點D處的橫向彎矩mAB、mDC分別為

(7)

(8)

X1、δh分別為頂板作用單位水平力時的頂板跨中剪力和側向位移，其值為

(9)

(10)

式中：X=X1/2；I1、I2、I4分別為腹板、底板、頂板的面外慣性矩.

2 板元分析法

采用板元分析法分析箱形梁的畸變效應時，將箱形梁頂板、底板、腹板離散為板元進行分析.各板元的面內力系如圖5所示.

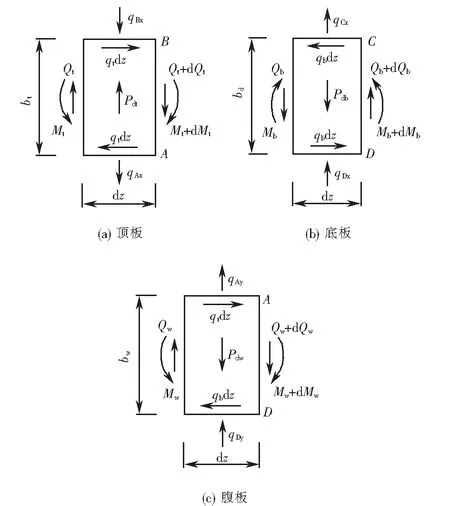
圖5 各板元面內力系Fig.5 In-plane forces of each plate

由各板板元上面內力系的平衡條件，可得

(11)

(12)

(13)

dQt=Pdt-qAx-qBx;

(14)

dQb=Pdb-qCx-qDx;

(15)

dQw=-Pdw+qAy+qDy.

(16)

式中：qt、qb為微段上腹板對頂板、底板的縱向約束荷載集度；qAx、qBx為腹板對頂板的橫向約束反力；qCx、qDx為腹板對底板的橫向約束反力；qAy、qDy為頂板和底版對左腹板的橫向約束反力；Qt、Qb、Qw為作用在頂板、底板、腹板微段上的剪力.

將式(11)、式(12)代入式(13)并微分一次，然后將式(14)、式(15)及式(16)代入，令qy=qAy+qDy；qx1=qAx+qBx；qx2=qCx+qDx可得

(17)

式(17)綜合反映了畸變翹曲變形、畸變框架變形與畸變荷載之間的關系.式(17)等式左邊可以拆解為與畸變翹曲變形、畸變框架變形、畸變荷載有關的三個分項W1、W2、W3，分別為

(18)

(19)

(20)

則式(17)可寫為

W1-W2+W3=0.

(21)

將式(4)～(6)代入式(18)可得

(22)

式中：

箱形梁發生畸變變形時各板元的平面外力系如圖6所示.圖中，mAB=mBA、mDC=mCD、mAD=mDA、mBC=mCB，分別為頂板、底板、左腹板、右腹板的板端彎矩；qBy、qCy分別為框架右腹板對頂板和底板的橫向約束反力.由平面外力系的平衡條件及框架橫向彎矩的反對稱性可得

(23)

(24)

(25)

將式(7)～(8)、(23)～(25)代入式(19)可得

W2=Γ3γD.

(26)

將式(1)～(3)代入式(20)，可得

(27)

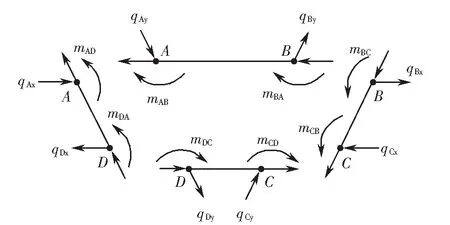
圖6 板元面外力系Fig.6 Out-plane forces of each plate

(28)

(29)

式中：λP為板元分析法中反映箱形梁抵抗畸變變形能力的幾何參數；EIWP為抗畸變翹曲剛度.

3 能量分析法

采用能量分析法分析箱形梁即便效應時，同樣選取畸變角γD為基本未知量，由畸變產生的內力、變形以及總勢能最終均表示為γD的泛函，通過變分得到畸變控制微分方程方程.箱形梁由于畸變翹曲變形和畸變框架變形產生畸變翹曲應變能和框架畸變應變能.由式(7)～(8)可得框架畸變應變能U1為

(30)

式中：

由式(4)～(6)可得角點D處的畸變翹曲正應力σD為

(31)

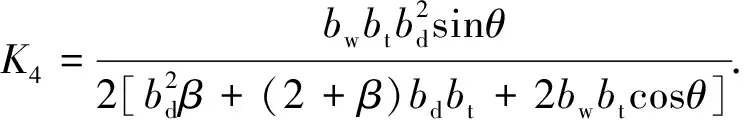
則畸變翹曲應變能U2為

在佛教中，“坐化”是指坐姿逝去。這種背景信息對英語讀者來說很陌生，所以譯者最好加上解釋。這里譯者用普通英語單詞來表達文化負載詞“坐化”，使讀者對中國佛教文化有一個簡單的了解。

(32)

式中：

箱形梁在畸變荷載作用下的外荷載勢能V為

(33)

當不考慮剪切變形時，箱形梁在畸變荷載作用下的總勢能Π=U1+U2+V.Π取極值的必要條件為Π的一階變分為零.由此可得畸變控制微分方程為

(34)

(35)

式中：λE為能量分析法中反映箱形梁抵抗畸變變形能力的幾何參數；EIWE為抗畸變翹曲剛度.

通過計算可以得到，采用板元分析法和能量變分法兩種不同方法計算得到的畸變幾何特性參數λP、λE相等[16]，采用板元分析法計算得到的抗畸變翹曲剛度EIWP為采用能量分析法計算所得值EIWE的兩倍，即滿足

λP=λE.

(36)

EIWP=2EIWE.

(37)

通過對比式(29)及式(35)右邊項可以得出，對于直腹板箱梁，即當bt=bd時，滿足

(38)

式(38)表明，對于直腹板箱形梁，當采用板元分析法和能量變分法分析箱形梁畸變效應時，兩種計算理論所得結果完全一致.

橋梁工程設計中根據不同的約束條件，關于畸變控制微分方程的邊界條件可表示為如下的形式：

1) 剛性固定的支座約束

箱形梁在剛性固定支座處不能發生畸變變形，因此畸變角與畸變位移均為零：

γ=0,γ′=0.

(39)

2) 簡支梁的端部設置有剛性橫隔板

橫隔板的約束使得箱形梁在梁段不能發生畸變變形，即畸變角為零，且在端部橫截面上的畸變翹曲正應力為零:

γ=0,γ″=0.

(40)

3) 自由懸臂端且沒有設置橫隔板

箱形梁在自由懸臂端畸變翹曲正應力與畸變翹曲剪應力均為零：

γ″=0,γ″′=0.

(41)

4 數值算例及參數分析

文獻[1]中的算例為一等截面簡支箱形梁橋，其跨度L=40 m，箱形梁的橫截面尺寸如圖7所示.該箱梁采用彈性模量E=3.4×104MPa的C40混凝土，并在梁端設置厚度為1.2 m的橫隔板.在箱形梁跨中頂板與左腹板交點處作用偏心荷載P=451.0 kN.分別采用板元分析法、能量分析法、ANSYS有限元法對該箱梁進行有限元分析計算.

圖7 箱形梁橫截面簡圖(單位：cm)Fig.7 Cross section of box girder (unit:cm)

本例箱形梁底板與左腹板交點處畸變翹曲正應力γD隨頂、底板長度之比bt/bd的變化曲線如圖8所示.在分析過程中，保持箱形梁頂板長度不變，通過改變箱形梁底板長度來實現頂、底板長度之比的變化.從圖中可以看出，采用板元分析法、能量分析法、ANSYS有限元法三種不同方法計算所得的畸變翹曲正應力均隨頂、底板長度之比bt/bd的增大而減小，采用有限元法計算時時降低幅度最大，采用板元分析法計算時降低幅度最小.當bt/bd=1時，板元分析法和能量分析法的計算結果相同.

不同頂、底板長度之比下畸變翹曲正應力γD的計算結果如表1所列.由表1可以得到，對于本例箱梁，當bt/bd<1.4時，采用板元分析法計算所得的畸變翹曲正應力與ANSYS有限元法計算所得結果更為接近；而當bt/bd>1.8時，采用能量分析法計算所得的畸變翹曲正應力與ANSYS有限元法計算所得結果更為接近.

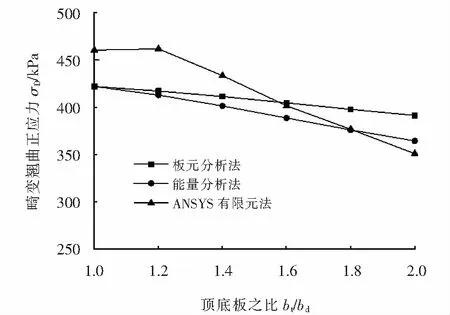
圖8 畸變翹曲正應力隨bt/bd的變化曲線Fig.8 Variation curve of distortion warping normal stress with bt/bd

表1 不同頂、底板長度之比下的畸變翹曲正應力

5 結論

1) 本文對比了板元分析法、能量分析法在分析箱形梁畸變效時的不同，從理論上證明兩種不同方法計算得到的畸變幾何特性參數λP、λE相等，且對于直腹板箱梁，兩種理論計算結果完全相同.

2) 采用板元分析法、能量分析法、ANSYS有限元法三種不同方法計算所得的畸變翹曲正應力均隨頂、底板長度之比bt/bd的增大而減小，采用有限元法計算時降低幅度最大，采用板元分析法計算時降低幅度最小.

3) 當bt/bd<1.4時，采用板元分析法計算所得本例箱梁的畸變翹曲正應力與ANSYS有限元法計算所得結果更為接近；而當bt/bd>1.8時，采用能量分析法計算所得的畸變翹曲正應力與ANSYS有限元法計算所得結果更為接近.