混合梁-塔斜拉橋力學特性及參數敏感性

張紫辰，王根會

(蘭州交通大學 土木工程學院，蘭州 730070)

混合梁斜拉橋主跨一般采用自重較輕的鋼箱結構，邊跨則用自重和剛度較大的預應力混凝土箱梁作為配重，從而有效減小梁體自身引起的內力和變形，具有跨越能力大和穩定性好等優點[1]，目前，國內已建成具有代表性的混合梁斜拉橋有萬州長江公路三橋、岳口漢江特大橋、深茂鐵路潭江特大橋等.其中，絕大多數斜拉橋索塔以鋼筋混凝土為主，少數有鋼索塔[2-3].近年來，鋼-混凝土混合索塔在大跨斜拉橋的建設中具有良好應用前景，如南京長江三橋、蘇通長江大橋和杭州灣主航道橋等斜拉橋的索塔都采用了混合結構，與鋼筋混凝土及鋼索塔相比，混合索塔下塔柱采用混凝土結構能夠承受較大的豎向壓力，而上塔柱鋼結構使拉索錨固區受力明確、構造簡單，并實現索塔輕量化[4]，中間用鋼混結合段把二者連接形成整體.

隨著混合橋梁結構的發展，學者們針對混合梁斜拉橋結構體系、力學性能和設計參數敏感性等方面都進行過深入研究，揭示了該類斜拉橋的力學特點及合理參數的取值[5-10].而對混合塔的研究則主要以鋼混結合段及下塔柱混凝土的受力特性為主[11-13].混合梁-塔斜拉橋具有混合梁和混合塔的雙重優勢，為高次超靜定結構，幾何非線性行為突出，受力復雜，結構整體剛度與傳統混合梁斜拉橋相差較大，同時參數敏感性分析在斜拉橋設計和施工階段都有著至關重要的作用.目前，國內關于混合梁-塔斜拉橋的研究較少.鑒于此，以海東大道1號斜拉橋為例，基于有限元法仿真分析，研究該類斜拉橋的力學特性，選取拉索張拉力、混凝土梁剛度、混凝土梁容重和鋼梁容重等參數進行結構敏感性分析.

1 工程背景

青海省海東大道1號斜拉橋全長243 m，寬44 m，是一座雙索面混合梁-塔斜拉橋，跨徑布置為158 m+45 m+40 m.其中輔跨45 m+40 m，為預應力混凝土結構，主跨長158 m，為鋼箱梁，梁高均為3 m；斜拉索采用扇形雙索面布置，每側有12對斜拉索.鋼梁采用正交異性流線型扁平鋼箱，斷面為單箱九室，腹板間距5 m左右.鋼混結合段長度為2.5 m，混凝土梁采用等截面預應力箱梁，C50混凝土.主塔由混凝土塔、鋼-混結合段、鋼塔三部分組成，塔高107 m.鋼塔和混凝土塔分別采用單箱雙室和單箱單室矩形截面.橋梁立面布置如圖1所示.

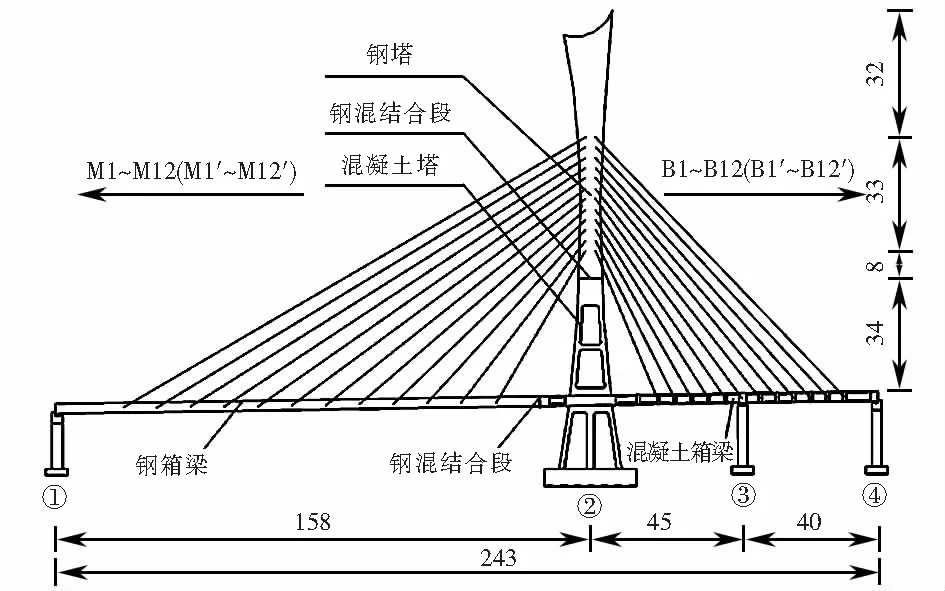
圖1 海東大道1號斜拉橋立面布置(單位：m)Fig.1 Elevation layout of No.1 Bridge on Haidong Avenue (unit:m)

2 結構有限元模型

利用有限元軟件Midas Civil建立分析模型，全橋共341個節點，梁單元205個，48個索單元，且充分考慮大位移效應和梁柱效應；墩頂與蓋梁之間采用剛性連接，拉索與主梁及橋塔間的連接采用彈性連接中的剛性模擬，塔墩梁固結部位采用剛性連接；考慮到樁-土相互作用對橋梁自振特性的影響，采用樁基模式模擬樁基礎，土彈簧使用節點彈性支撐[14].全橋有限元模型如圖2所示.

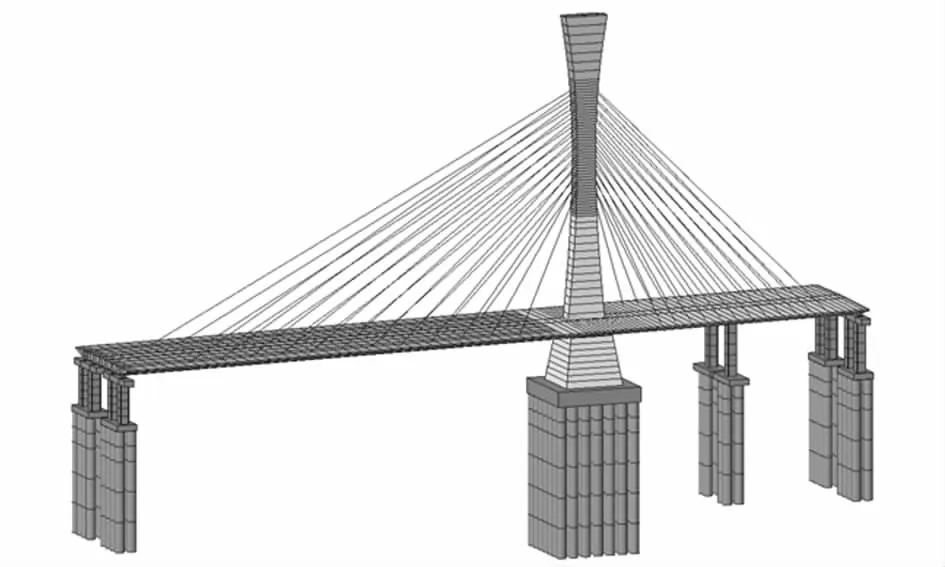
圖2 全橋有限元模型Fig.2 Finite element model of the whole bridge

3 混合梁-塔斜拉橋力學特性

3.1 斜拉索無應力索長計算

斜拉索無應力長度指拉索處于零應力狀態下的長度.實際工程中，常采用懸鏈線與拋物線法分析斜拉索的無應力索長，由于混合梁-塔斜拉橋受混凝土收縮徐變的影響較全鋼箱梁斜拉橋大，所以輔跨拉索無應力長度需考慮混凝土收縮徐變影響，運用懸鏈線與拋物線法求得海東大道1號斜拉橋的部分拉索無應力長度如圖3所示.

由圖3可知，懸鏈線與拋物線法計算結果分布規律基本一致，但懸鏈線法無應力索長計算值偏大，二者最大差值在M8號索，為3.3 mm，結合青州航道橋計算結果可知[15]，當混合梁-塔斜拉橋跨徑小于500 m時，采用拋物線法計算拉索無應力長度可滿足工程要求.

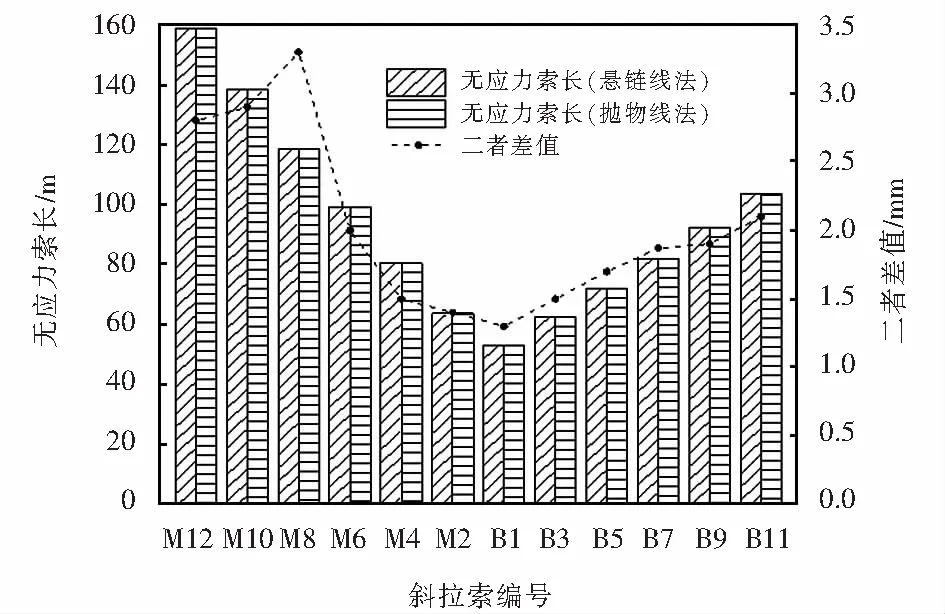
圖3 不同計算方法所得無應力索長對比Fig.3 Comparison of unstressed cable length obtained by different calculation methods

3.2 施工成橋狀態靜力特性

基于施工過程跟蹤，分別按照考慮和不考慮幾何非線性計算得到混合梁-塔斜拉橋施工成橋狀態下的結構彎矩、位移和索力對比如圖4所示.

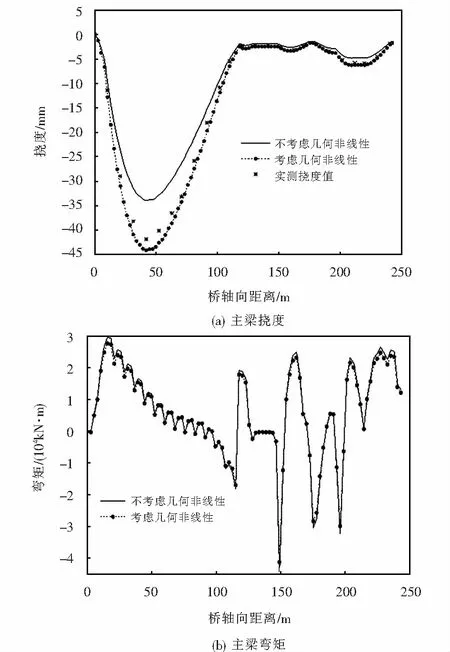
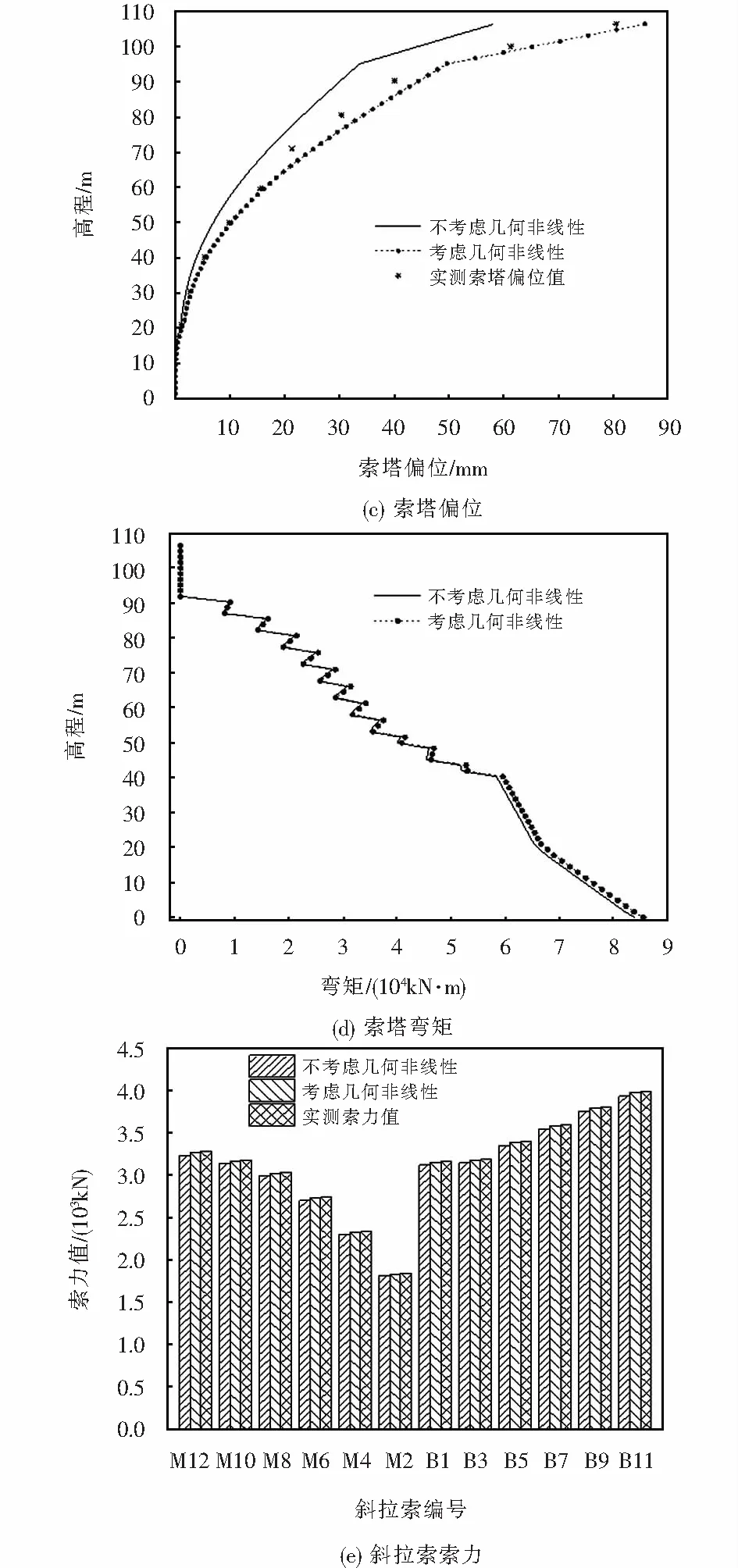
圖4 幾何非線性對結構施工成橋狀態受力性能的影響Fig.4 Influence of geometric nonlinearity on mechanical performance of completed bridge under construction

由圖4可知，幾何非線性對混合梁-塔斜拉橋變形影響較大，考慮幾何非線性時，主梁撓度和塔頂偏位與實測值吻合良好，且較不考慮幾何非線性分別增大9 mm和27 mm，達26.5%和45.8%；幾何非線性對主梁彎矩和索力的最大影響程度分別為0.78%和1.21%，對索塔彎矩的影響最大為3.2%，說明幾何非線性對結構內力影響較小，但由于索塔自身彎矩較大，微小的偏差也會造成較大的絕對誤差，因而建議設計和施工模擬中應充分考慮該類斜拉橋的幾何非線性.

3.3 運營階段靜力特性

在考慮幾何非線性計算得到施工成橋狀態的基礎上，結合汽車荷載和人群荷載等因素分析結構靜力特性，斜拉橋控制截面的最大內力和位移值如表1所列，相應的結構內力和位移包絡圖如圖5所示.計算時，汽車荷載按照公路-I級雙向六車道加載，依據規范[16]，荷載組合形式為1.0永久荷載+1.4汽車荷載+1.05人群荷載.

表1 結構最大內力和位移值

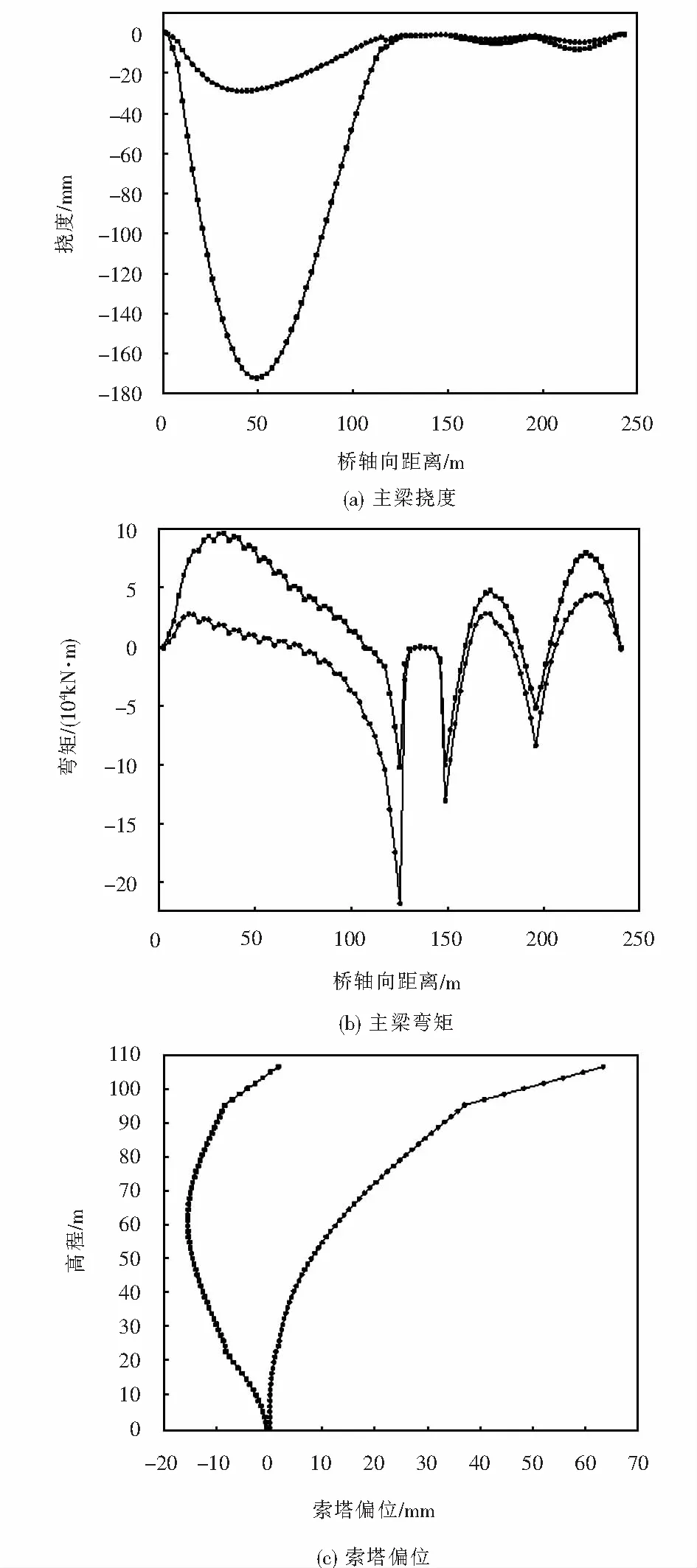
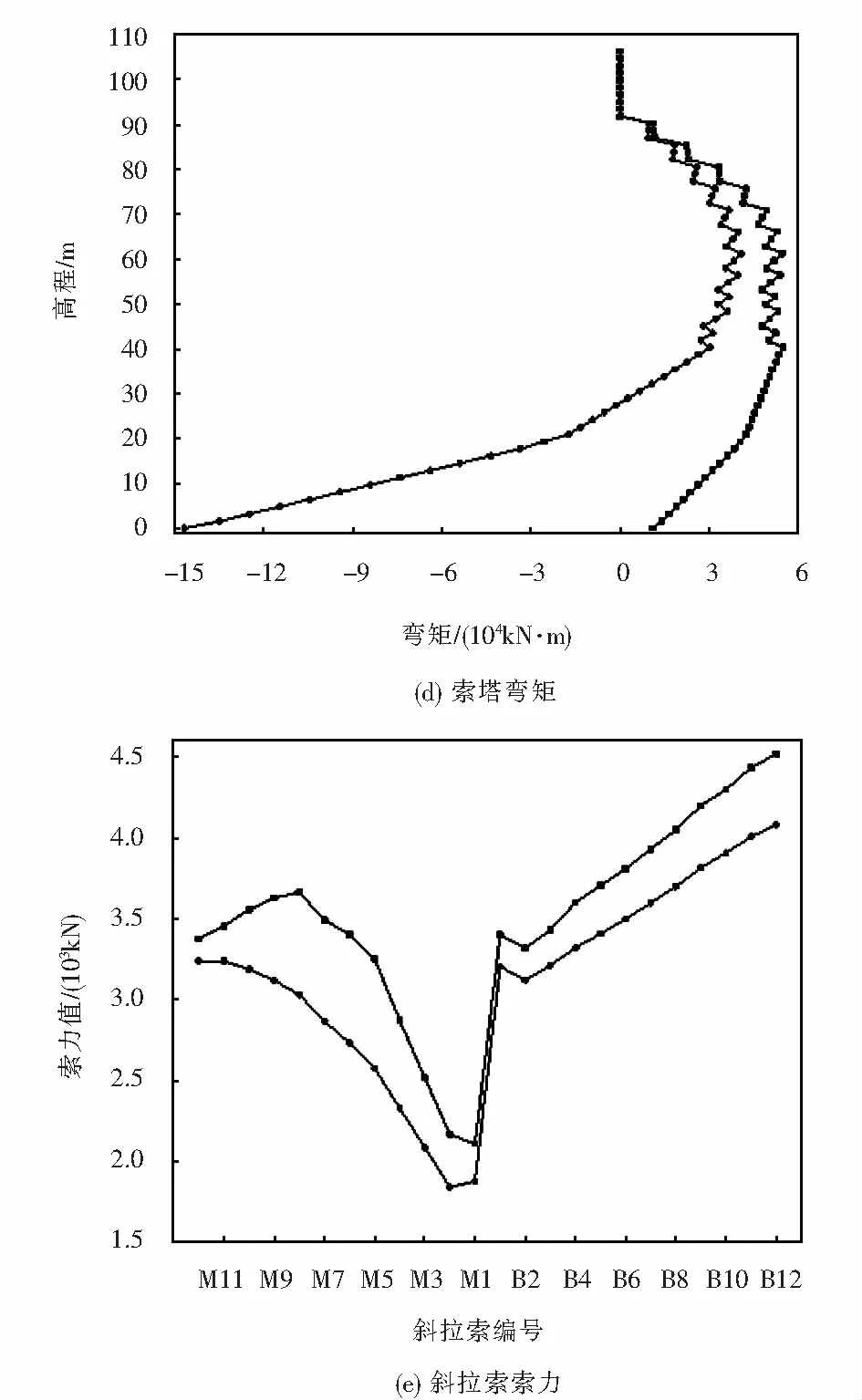
圖5 結構內力和位移包絡圖Fig.5 Envelope diagram of structural internal force and displacement

由表1和圖5可知，主梁在恒活載作用下的最大豎向位移為17.2 cm，小于規范規定的最大限值，說明主梁剛度滿足設計要求，塔頂偏向主跨側最大位移為6.3 cm，說明混凝土梁對索塔和主跨鋼梁的變形控制較好；恒活載作用下主梁最大正彎矩為96 759.22 kN·m，最大負彎矩-218 303.45 kN·m，均出現在鋼梁上，受混凝土主梁剛度的影響，中跨主梁的彎矩變幅明顯減小.

3.4 混合梁-塔斜拉橋動力特性

在結構有限元分析中，為簡化計算，多數情況下會對橋墩底部做固結處理而忽略樁土之間的相互作用.由文獻[17]可知，樁土相互作用會使橋梁的自振特性、阻尼和地震反應等發生改變，本文將分別計算考慮和不考慮樁土作用下海東大道1號橋的自振特性，分析樁土相互作用對混合梁-塔斜拉橋動力特性的影響.海東大道1號橋的前十階頻率及振型對比如表2所列.

表2 海東大道1號橋頻率及振型對比

由表2可知，考慮樁土相互作用后，結構的動力特性變化明顯，多維耦合振型增多，高階振型相差較大，對應階數的頻率值減小，但頻率值分布較不考慮樁土相互作用的承臺底固結模型密集；結構一階振型表現為索塔橫彎，說明索塔采用混合結構后剛度減小，主梁豎彎以鋼結構為主，體現了混凝土主梁剛度大的特點；同時，其高階振型出現了過渡墩縱彎，主要是由于過渡墩處安裝了雙向活動支座造成的.

4 參數敏感性分析

結合海東大道1號橋斜拉橋監控情況可知，輔跨側混凝土梁在澆筑施工時，由于混凝土密度誤差和脹模等原因，導致混凝土梁段自重和強度普遍偏大，超出設計值的幅度在4.6%以內，而主跨鋼箱梁梁段在工廠預制時精度較高，誤差相對較小；同時，該斜拉橋拉索分兩次張拉，施工時受風力、溫度和結構振動等因素的影響，很難保證張拉力值剛好等于設計值.因此，考慮施工階段幾何非線性的影響，選取斜拉索初張力、主梁剛度和主梁容重等參數作為變量，以設計值作為基準狀態，通過單因素變量法進行敏感性分析[18].上述參數變化時，施工成橋階段的結構狀態控制目標包括主梁豎向位移、主梁彎矩和斜拉索索力.

敏感性分析時，假定主跨鋼箱梁剛度與設計值一致，分別讓輔跨混凝土梁段容重和剛度增大5%、鋼主梁梁段容重增大2%及每根拉索最后一次張拉控制力增大5%，分析單參數變化對施工成橋狀態下結構主梁豎向位移、主梁彎矩和斜拉索索力的影響.

4.1 主梁位移參數敏感性

混合梁-塔斜拉橋主梁在成橋階段的位移大小反映了結構的整體剛度，各參數變化對斜拉橋施工成橋階段主梁豎向位移的影響如圖6所示.

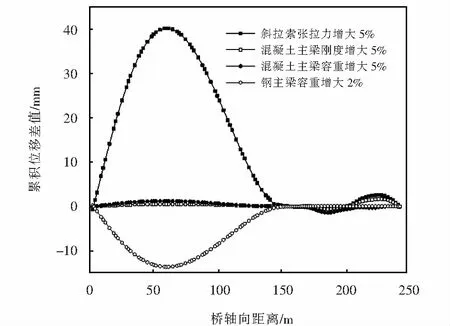
圖6 主梁豎向位移影響圖Fig.6 Influence diagram of vertical displacement of main girder

由圖6可知，主梁豎向位移受拉索張拉力的影響較大，當拉索張拉力增大5%時，主跨鋼梁標高明顯變大，跨中累積位移差達到41.3 mm，但輔跨側混凝土梁位移變化較小，最大位移差為4.6 mm；鋼主梁容重增大2%時，主跨鋼梁跨中下撓15.2 mm，而輔跨側混凝土梁位移幾乎沒有變化；同時，混凝土梁容重和剛度的變化對主梁豎向位移的影響相對較小，保持在3.4 mm以內.所以，基于主梁線形考慮，拉索張拉力和鋼梁容重對主梁豎向位移影響顯著，為主要影響參數，輔跨混凝土梁主要其錨固作用，其容重和剛度的變化對主梁線形影響較小，為次要影響參數.

4.2 主梁彎矩參數敏感性

各參數變化對混合梁-塔斜拉橋施工成橋階段主梁彎矩的影響如圖7所示.

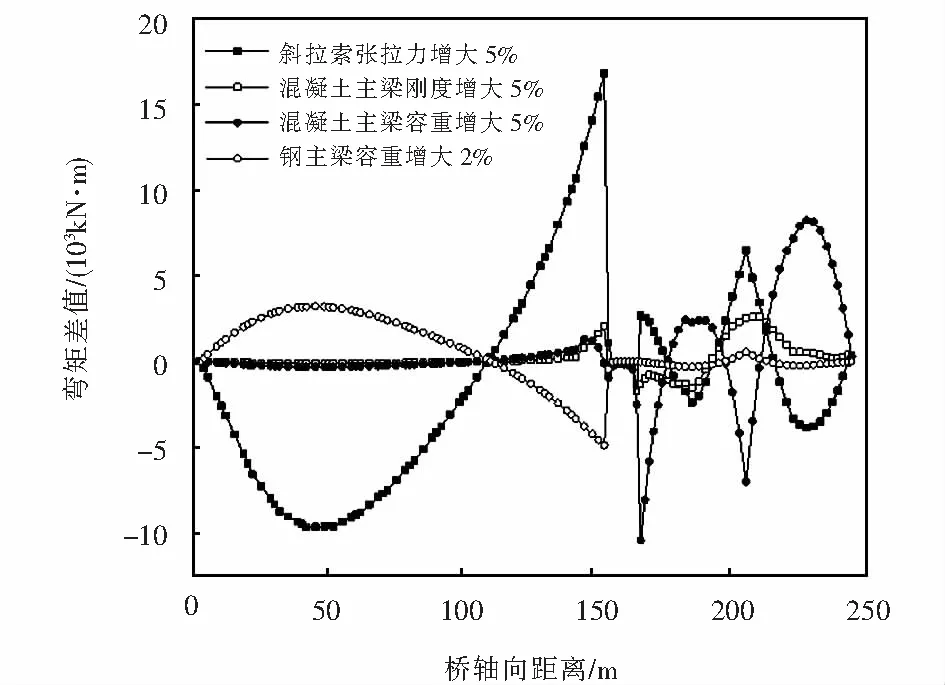
圖7 主梁彎矩影響圖Fig.7 Influence diagram of main girder bending moment

由圖7可知，當拉索張拉力增大5%時，主梁彎矩變化明顯，最大彎矩差出現在塔梁固結端左側位置，其值為16 829.1 kN·m；鋼梁容重的變化主要影響鋼梁主的彎矩，對輔跨側混凝土梁彎矩的影響較小；混凝土梁容重和剛度變化時輔跨側混凝土主梁彎矩有較大變化，而鋼梁主彎矩的變化則較小；但總體而言，混合梁-塔斜拉橋主梁彎矩對拉索張拉力、鋼梁容重、輔跨混凝土梁容重和剛度的變化都是較敏感的.

4.3 斜拉索索力參數敏感性

各參數變化對混合梁-塔斜拉橋施工成橋索力的影響如圖8所示.

由圖8可知，拉索張拉力的變化對其施工成橋索力的影響顯著，當張拉力增大5%時，斜拉索成橋索力普遍增大，其中輔跨側拉索B12成橋索力變化值達151.2 kN；鋼主梁容重對結構主跨側拉索成橋索力的影響大于輔跨側拉索的成橋索力，而混凝土梁容重和剛度的變化對成橋索力的影響很小，即拉索張拉力和鋼主梁容重為結構成橋索力的主要影響參數，輔跨混凝土梁容重和剛度的變化對成橋索力影響不大，為次要影響參數. 綜合四種參數影響指標而言，拉索張拉力對斜拉橋施工成橋階段的主梁豎向位移、彎矩和成橋索力影響最大，其次為鋼主梁容重，二者為主要影響參數，在橋梁模型計算時需要進行修正；混凝土主梁容重和剛度的變化對結構力學性能的影響較小，為次要影響參數，在橋梁模型修正時可以忽略.

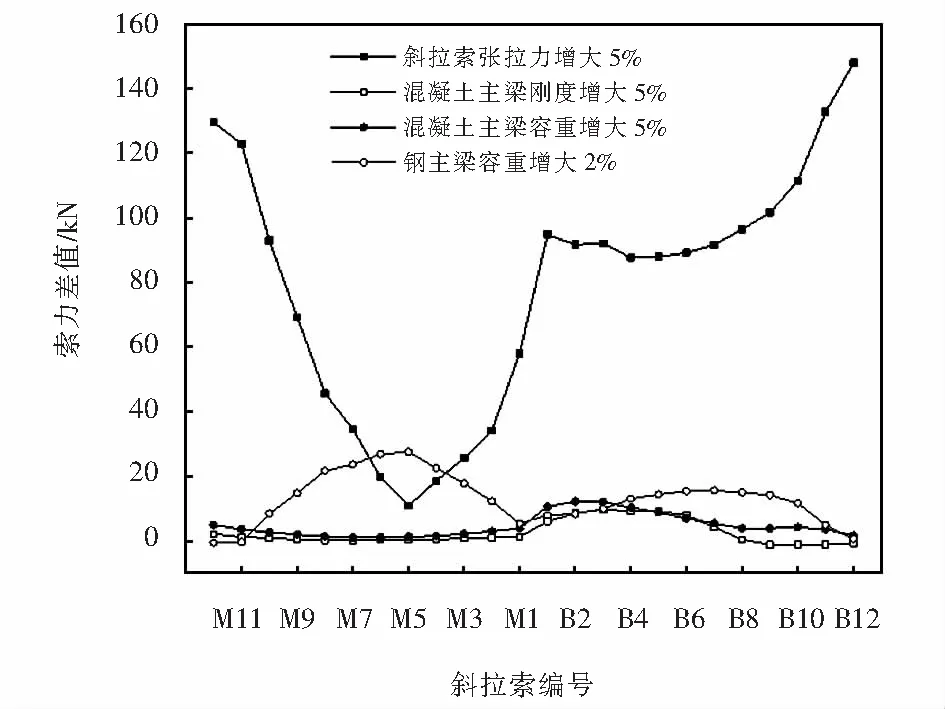
圖8 斜拉索索力影響圖Fig.8 Influence diagram of stay cable force

5 結論

本文以海東大道1號斜拉橋為工程背景，建立了空間有限元模型，研究了該類斜拉橋的力學特性，分析了拉索張拉力、混凝土梁剛度、混凝土梁容重和鋼梁容重等參數對其施工成橋階段力學性能的敏感性.得出以下結論：

1) 幾何非線性對混合梁-塔斜拉橋內力影響較小，但對其變形影響很大，考慮幾何非線性時，該斜拉橋主梁撓度和塔頂偏位分別增大了26.5%和45.8%，因而設計和施工模擬中必須充分考慮該類斜拉橋的幾何非線性；且斜拉橋跨徑小于500 m時，采用拋物線法計算拉索無應力長度可滿足工程設計要求；

2) 考慮樁土相互作用后，結構多維耦合振型增多，對應階數的頻率值減小，但頻率值分布較不考慮樁土相互作用的承臺底固結模型密集；結構一階振型表現為索塔橫彎，主梁豎彎振動以鋼結構為主，體現了混凝土主梁剛度大的特點；

3) 綜合四種參數影響指標，拉索張拉力對混合梁-塔斜拉橋施工成橋階段的力學性能影響最大，其次為鋼主梁容重，在該類橋梁模型計算時需要對二者進行參數修正.