兩個重要恒等式在同構法中的應用
廣東省佛山市第一中學 (528000) 劉振興
在解決指對數混合不等式時,如恒成立求參數取值范圍或證明不等式,如果用隱零點代換或某種意義上求根,計算復雜,同構法會給我們的解題帶來極大的便利.在成立或恒成立問題中,有一部分試題是命題者利用函數單調性構造出來的,如果我們能找到這個函數模型(即不等式兩邊對應的同一函數),無疑大大加快解決問題速度,找到這個函數模型的方法,我們稱為同構法.
先來看2021年廣東四校聯考第22題.
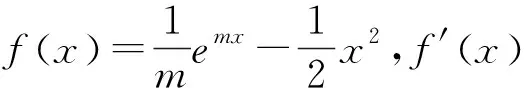
(1)若m=1,x∈R,求函數g(x)=f(x)+f(-x)的最小值;

證明:(1)略.
(法二)法一中的等價變換也可以如下變化:
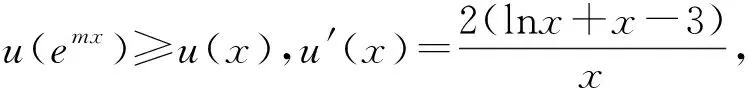
評注:本題學生得分很低,很多學生對同構法不熟悉,不會應用.法一中①式利用了恒等式a=elna,法二中②式利用了恒等式a=lnea,這兩個恒等式也是在指對數同構中經常用到的恒等式.
在處理具體指對數同構題時,利用恒等式a=elna和a=lnea可以產生如下常見的五個變形.
一、五個常見變形
例1 (2021年湖北宜昌市聯考)若不等式x-4ex-alnx≥x+1對任意x∈(1,+∞)恒成立,求實數a的取值范圍.
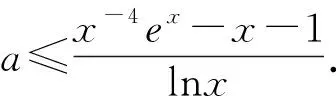
利用恒等式a=elna和a=lnea,可以用同構法解決如下三種題型的導數題.
二、幾種常見題型
題型1積型
三個常見的能化成積型的變形:
(1)λxeλx≥xlnx?λxeλx≥(lnx)·elnx→構造f(x)=xex或f(x)=xlnx;
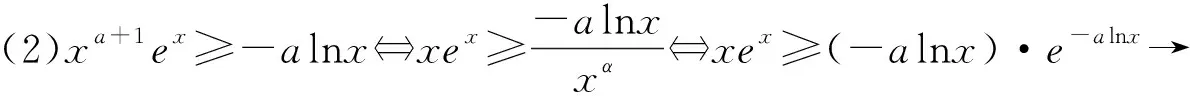
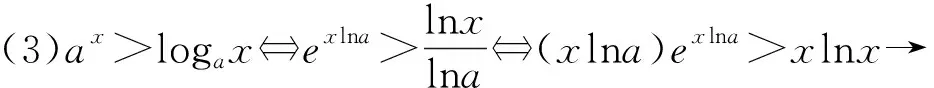
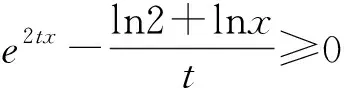
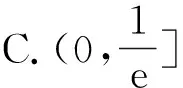
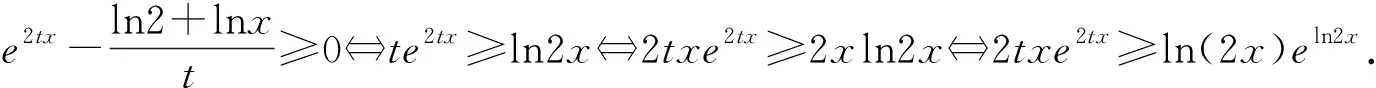
題型2商型
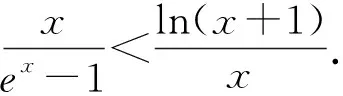
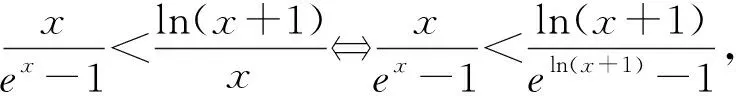
題型3和差型
1.兩個常見的能化成和差型的變形.
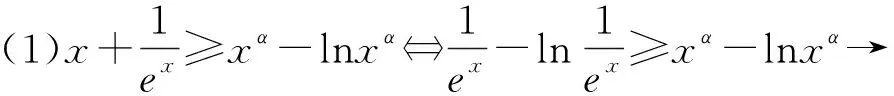
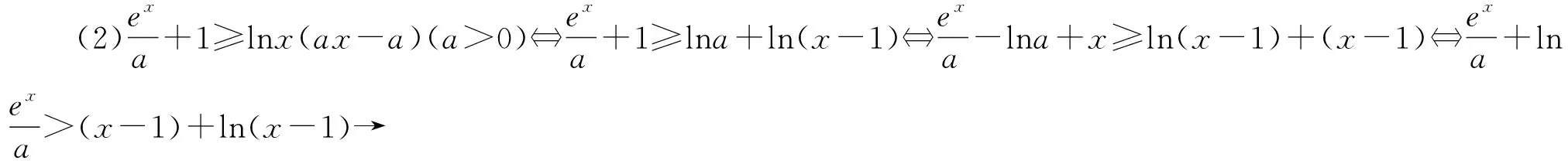
例4 (2019年武漢市江岸區模擬題)已知函數f(x)=ex-aln(ax-a)+a(a>0),若關于x的不等式f(x)>0恒成立,則實數a的取值范圍為( ).
A.(0,e2] B.(0,e2) C.[1,e2] D.(1,e2)
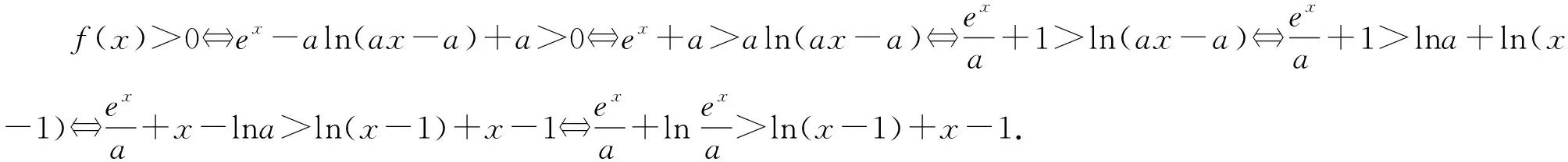
2.積型轉化成和差型,商型轉化成和差型
積型aea 例5 (2020年新高考山東)已知函數f(x)=aex-1-lnx+lna. (1)當a=e時,求曲線y=f(x)在點(1,f(1))處的切線與兩坐標軸圍成的三角形的面積;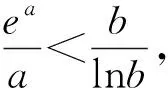
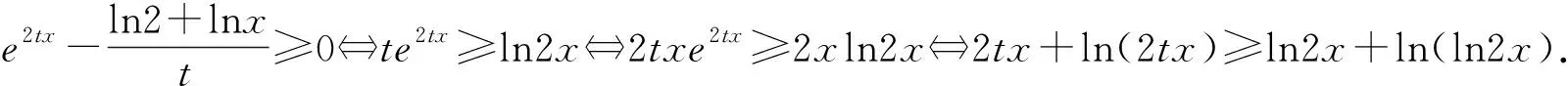
三、高考中的應用

