例談三角函數(shù)周期性問題

江蘇省無錫市第一中學(xué) (214100) 吳明飛

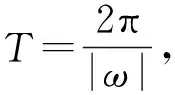
一、教學(xué)分析

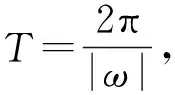
二、教學(xué)過程

(一)解三角函數(shù)的周期問題時(shí)如何思考

教學(xué)片斷1

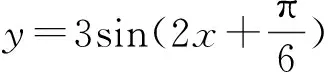
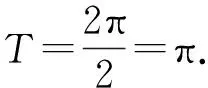
教學(xué)目的：鞏固學(xué)生對(duì)常規(guī)三角函數(shù)周期性問題的求解，學(xué)會(huì)通性通法.

教學(xué)片斷2

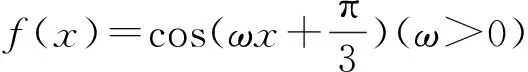
A.最小值為2 B.最大值為2

C.最小值為1 D.最大值為1

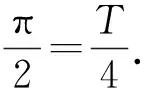
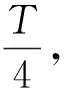
(二)學(xué)習(xí)三角函數(shù)的周期性需要注意什么

教學(xué)片斷3

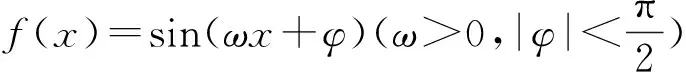
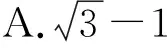
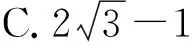
這是一道新高考模擬題，學(xué)生們的做題思路還是比較明確，其大部分同學(xué)的做法大是這樣的：

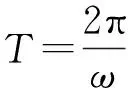
反思辨析：仔細(xì)分析發(fā)現(xiàn)，這里有個(gè)概念性的錯(cuò)誤，由f(x+2π)=f(x)得到2π為f(x)的一個(gè)周期，但是不一定是最小正周期，但后面的運(yùn)算學(xué)生們都是默認(rèn)為最小正周期的，所以上述做法不對(duì)，所以在處理三角函數(shù)的周期問題時(shí)，一定要區(qū)分開周期與最小正周期，所以此題值得深入研究.

分析：既然由f(x)=-f(x+π)得不到最小正周期，但f(x)=-f(x+π)肯定是有意義的，即對(duì)任意x∈R，f(x)=-f(x+π)恒成立，直接代入解析式得，通過代數(shù)變形得到sin(ωx+φ)=-sin(ω(x+π)+φ)=sin(-ωx-ωπ-φ)=sin(π+ωx+ωπ+φ)，sin(ωx+φ)=sin((ωx+φ)+(π+ωπ))，所以π+ωπ=2kπ,k∈Z，即ω=2k-1,k∈Z，又因?yàn)棣?0，此時(shí)發(fā)現(xiàn)ω可以取無窮多個(gè)數(shù)，這與出題人想展示的不是一個(gè)意思，所以此題是有問題的，不能確定ω，若把“ω>0”改為“0<ω<2”即可確定ω的值為1，最終答案選A.

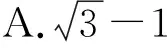
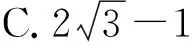
還可以繼續(xù)如下分析：

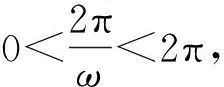
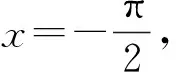
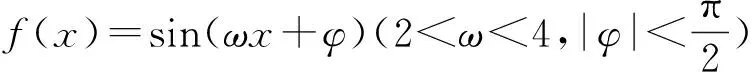
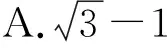
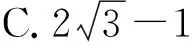
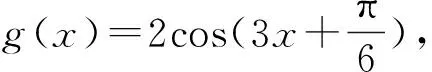
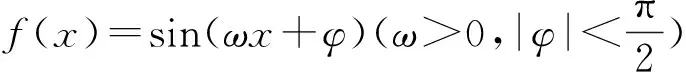
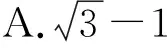
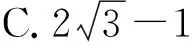
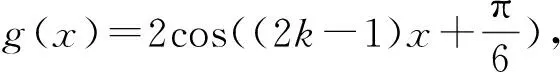
反思總結(jié)：在學(xué)習(xí)三角函數(shù)的周期時(shí)，我們要注意周期與最小正周期的區(qū)別，容易混淆而導(dǎo)致錯(cuò)誤.對(duì)于三角函數(shù)中的代數(shù)變形含義的理解，要做到準(zhǔn)確，如例3中，化簡(jiǎn)完之后是一個(gè)恒成立問題，所以要做到對(duì)問題的深入理解.在做選擇題時(shí)可以大膽的假設(shè)，通過合理論證可以解決問題；或者可以通過特殊值方法，通過檢驗(yàn)來說明選項(xiàng)的正確性.……