基于Canopy-K-means算法的半掛汽車列車行駛數據分析

李 兵， 屈亞洲， 熊 樂， 王曉亮， 趙晨光

(中汽研汽車檢驗中心(寧波)有限公司， 浙江 寧波 315336)

近年來，隨著物流運輸業的快速發展，半掛汽車列車在商用車市場的占比逐年增加。據統計[1]，2013—2017年國內半掛牽引車年銷量整體呈遞增趨勢，且2016和2017兩年的年銷量較上一年同比增長了55%和50%。而半掛汽車列車作為誘發重大交通安全事故的主要源頭之一，其數量的增加勢必會給其他交通參與者帶來更多的潛在危險，因此，如何提高汽車列車行駛安全性一直是行業的研究熱點。

Singh[2]利用相平面法提出了一定初始條件下半掛汽車列車系統相軌跡趨近和背離平衡點的變化規律，由此判定車輛的穩定和不穩定區域。關志偉等[3]采用線性系統穩態轉向特性、非線性系統穩態轉向特性和能量相平面3種方法對車輛轉向穩定性進行了分析。李西濤[4]建立了半掛汽車列車非線性動力學模型，分析了其在極限工況下各狀態變量平衡點的分岔現象，探討了極限操縱工況下車輛的橫向失穩機制。Ding等[5]利用分岔理論分析了恒定運行工況下半掛汽車列車非線性模型的穩定性，采用數值求解得到系統的穩定平衡點和不穩定平衡點，解釋了常見的不穩定現象，并對狀態空間中的穩定域進行了劃分。陳林[6]基于卡爾曼濾波算法建立了以半掛牽引車的側向加速度和橫擺角速度為觀測變量的狀態估計器，并選擇雙移線和方向盤角階躍工況試驗對半掛汽車列車狀態進行了估計分析。劉煥[7]建立了半掛汽車列車三自由度線性和非線性動力學模型，探究了車輛在不同行駛條件下的運動響應和失穩形式，并從能量變化角度對車輛的失穩機理進行解釋，為判定車輛失穩提供了新的依據。彭濤等[8]基于Lyapunov法分析了車輛極限狀態下的能量和能量變化閾值，求解得到半掛汽車列車高速變道穩定域，為車輛高速轉向時的穩定性判定提供依據。綜合以上文獻可知，現有對半掛汽車列車穩定性分析大多是基于簡化動力學模型進行的研究，存在所建模型不精確的問題。

為了解決這一問題，徐強[9]提出了一種基于K均值聚類分析的車輛橫向穩定性判定方法，通過對車輛仿真數據進行聚類分析，劃分了4種不同行駛狀態，并設計仿真試驗驗證了該方法在雙半掛汽車列車穩定性判定上的有效性，但是其聚類算法中的K值由經驗確定，具有一定的主觀性，影響對車輛行駛狀態的準確劃分，同時未進行實車試驗驗證該算法的有效性。翟德[10]利用K均值聚類算法對半掛汽車列車側翻和折疊工況進行了研究，進一步驗證了該方法在不同失穩形式下應用的有效性，但其缺點與文獻[9]類似。基于以上考慮，本文首先采用Canopy算法對車輛行駛數據進行“粗”聚類分析，確定k值和初始狀態聚類質心，然后在此基礎上利用K-means算法對車輛行駛狀態進行精確劃分，并將仿真試驗和實車試驗結果相結合驗證該方法的有效性。

1 系統建模

1.1 整車建模

由于本文主要從數據層面對半掛汽車列車行駛穩定性進行分析，需要大量的車輛行駛數據作為研究支撐，因此為了采集多工況下的行駛數據，選擇TruckSim軟件進行車輛動力學建模仿真，仿真所使用的車輛類型為3A Cab Over w/3A Euro Trailer。

1.2 仿真工況設計

依據《營運車輛抗側翻穩定性試驗方法 穩態圓周試驗》(JT/T 884—2014)和《商用車輛電子穩定性控制系統性能要求及試驗方法》(GB/T 8185—2019)試驗工況要求進行仿真工況設計，見表1。

表1 仿真工況設計

表1中，定半徑變車速選擇速度為30～70 km/h，以5 km/h的間隔依次進行仿真工況設計，這里只以速度為變量，不考慮方向盤轉角變化的影響；定車速變轉角選擇車速為40～60 km/h，方向盤轉角為30°、60°、90°、120°，速度間隔為5 km/h依次進行仿真工況設計；J轉向試驗選擇速度30～45 km/h，間隔為5 km/h，同樣不考慮方向盤轉角的影響。

2 車輛行駛數據分析

2.1 傳統的K-means算法

K-means是一種簡單的迭代型聚類算法，由于簡單易修改、運行速度快，在數據挖掘領域應用非常廣泛。其基本原理是：首先給定包含n個對象的樣本集和聚簇個數k，然后從樣本集中隨機選擇k個對象作為初始聚類質心，計算剩余樣本集與初始聚類質心的歐氏距離，并將它們分配給與其歐氏距離最小的聚簇，再重新計算每個聚簇中各數據對象的均值作為新的聚類質心，不斷重復這一過程直到各個聚簇的聚類質心不再變化或滿足停止條件，從而實現同一聚簇中的對象相似度較高，而不同聚簇中的對象相似度較小，完成對樣本集的劃分。

由于K-means算法中的聚簇個數k必須預先給定，且初始聚類質心的選擇是隨機的，容易在迭代過程中形成大量冗余，使聚類結果陷入局部最優解[11]。因此，針對上述問題以及縮短聚類時間周期，采用Canopy-K-means聚類算法[12-13]對車輛行駛數據進行聚類劃分。

2.2 基于Canopy優化的K-means算法

Canopy算法也是一種常見的聚類算法，是采用快速近似距離度量和兩個距離閾值比較方式，實現快速粗聚類[14]，由于其無須提前預設聚簇個數，因此可以在預處理階段對車輛行駛數據進行“粗”聚類，確定聚簇個數k和初始聚類質心，然后再利用K-means算法進行“細”聚類，提高聚類結果的準確性。

Canopy-K-means算法流程如圖1所示，可知在聚類工作開始之前，只需確定Canopy算法中的兩個距離閾值T1、T2(T1>T2)，K-means算法的迭代次數和目標函數的終止條件即可。

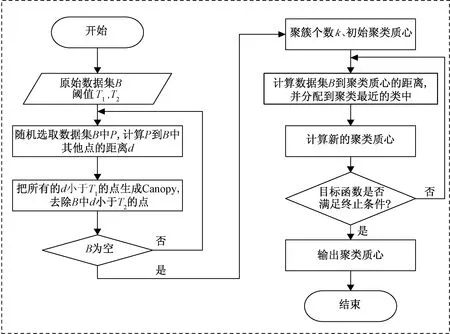
圖1 Canopy-K-means算法流程

2.3 數據挖掘分析

根據1.2節設計的仿真工況進行仿真，得到各個工況下的車輛行駛數據。考慮到實車試驗測試設備的可測變量，這里選取牽引車和掛車橫擺角速度(w1、w2)、質心側向加速度(ay1、ay2)和車身側傾角(ψ1、ψ2)6個狀態變量作為表征半掛汽車列車行駛穩定性的評價參數。結合各個工況的行駛特性，截取抗側翻穩定性試驗工況穩定時10 s的數據，截取J轉向試驗工況30 s的數據，采集共20 500組數據。為了便于對數據進行批量處理，將各個工況下采集的數據記為同一矩陣B=[w1i、w2i、ay1i、ay2i、ψ1i、ψ2i]，其中，角標i代表矩陣B的行數，也即是某運行工況下某一時刻的車輛狀態參數。

通過Canopy算法對矩陣B進行預處理，得到聚簇個數k=4，初始聚類質心

然后將Canopy的聚類結果代入K-means算法，得到的聚類結果如圖2所示，每種聚類質心代表車輛的一種行駛狀態。

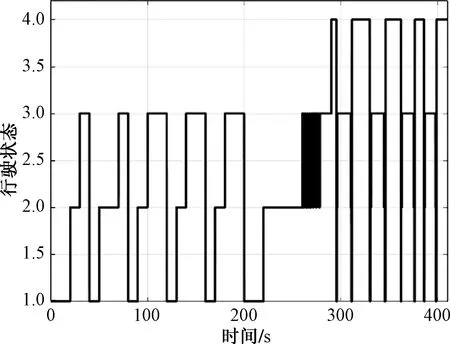
圖2 離線聚類結果

由圖2可知，經過聚類之后，這些數據被自動化分為4個行駛狀態，其中0～200 s為定車速變轉角工況，0～40 s表示速度為40 km/h，方向盤轉角為30°、60°、90°、120°時車輛的行駛狀態變化，可以發現車輛在方向盤轉角為30°和60°時為1狀態，當轉角增加到90°和120°時，車輛由1狀態到2狀態再變為3狀態；40～200 s表示速度為45～60 km/h，在相同方向盤轉角變化下，車輛行駛狀態變化，其與 40 km/h 的狀態變化類似，可知不同行駛狀態的危險性高低依次為3、2、1。200～290 s是定半徑變車速工況，隨著車速的增加，車輛側向加速度越來越大，穩定性降低，此時車輛的行駛狀態也呈現1-2-3變化。290～410 s是J轉向試驗工況，表征30～45 km/h 下車輛的行駛狀態，由于截取的是車輛剛進入彎道到駛出彎道的數據，車輛主要在3和4行駛狀態變化，且當車輛在彎道行駛時，此時車輛處于4狀態。綜合以上分析可以得到：車輛不同行駛狀態的危險性高低依次為4、3、2、1。

最后通過分析各聚類質心的特征值大小以及圖2分析的行駛狀態危險性高低，對聚類結果進行排序，結果見表2。

表2 基于Canopy-K-means算法得到的聚類質心

為了便于后續分析以及考慮到各特征值大小，這里參照文獻[15]的方法對各行駛狀態概括為3種危險等級狀態。其中，行駛狀態1和2統稱為安全的行駛狀態，行駛狀態3為危險演化階段，行駛狀態4為潛在危險。

3 在線仿真平臺搭建

3.1 工況設計

2.3節對車輛行駛數據進行了聚類分析，得到4種行駛狀態類型，并根據各工況行駛特點，對各行駛狀態下車輛的穩定性進行分析，獲得各行駛狀態的危險性高低依次為4>3>2>1。由于上述結論是基于不同工況下的行駛數據離線聚類得出的結果，因此這里選擇抗側翻穩定性和方向盤斜階躍輸入兩種試驗，來驗證聚類結果的有效性，其中抗側翻穩定性試驗工況參數設置見表3，方向盤斜階躍輸入工況設計如圖3所示。

表3 抗側翻穩定性試驗仿真工況設計

圖3為方向盤轉角隨時間的變化曲線，其中0～2 s，方向盤轉角為0°，車輛保持直線行駛，在2～10 s 方向盤轉角勻速增加，在第10 s時達到180°，并保持180°不變，直至仿真結束。

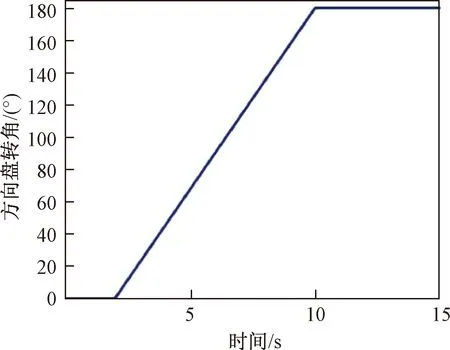
圖3 方向盤斜階躍輸入

3.2 在線識別

利用TruckSim和Simulink搭建了聯合仿真平臺，編寫了計算歐氏距離的MATLAB Function函數，根據表3和圖3所示工況依次進行仿真，其中表3所示工況只截取穩態行駛狀態下10 s內的行駛數據進行分析，共500組數據，具體仿真處理結果如圖4、圖5所示。

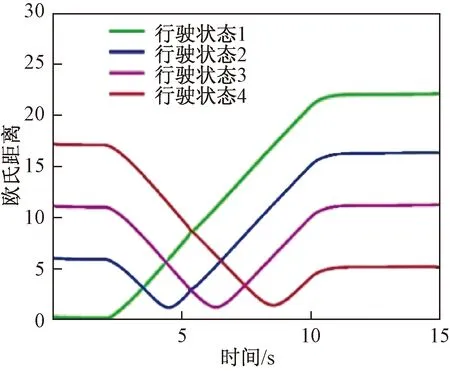
圖5 方向盤斜階躍輸入工況的歐氏距離在線識別

由圖4可知，在0～10 s，車速為40 km/h時，處于第2行駛狀態，此時車輛為安全狀態；在10～20 s，車速為45 km/h時，車輛在第2和3行駛狀態之間變化，表明車輛此時處于安全狀態向危險演化狀態的過渡階段；在20～50 s，速度為50～60 km/h時，車輛一直維持在第3行駛狀態，表明此時車輛處于危險演化狀態。

由圖5可知，在0～2 s直線行駛時，處于第1行駛狀態，此時車輛為安全狀態；在2～10 s方向盤轉角勻速增加時，由第1、2行駛狀態向3、4行駛狀態變化，此時車輛逐漸由安全狀態向危險演化狀態和潛在危險狀態過渡；在10～15 s保持方向盤轉角為180°不變時，處于第4狀態，此時車輛處于潛在危險狀態。

綜合以上兩種試驗工況的分析結果可知，在已知車輛行駛穩定性變化趨勢的情況下，與根據離線聚類結果在線計算歐氏距離判定得到的行駛狀態基本一致。因此，利用離線聚類結果對抗側翻穩定性試驗和方向盤斜階躍輸入工況的行駛穩定性判定是有效的。

4 實車驗證

為了進一步驗證聚類結果的準確性，這里以3.1節所列的試驗工況進行實車試驗，抗側翻穩定性試驗工況下行駛數據的選取方式與3.2節相同，同樣只截取穩態行駛狀態下10 s內的行駛數據，計算其與離線得到的聚類質心的歐氏距離。但考慮到實車試驗的安全性以及內容研究的側重點，半掛汽車列車選擇在空載的試驗條件下進行，試驗樣車如圖6所示。

圖6 試驗樣車

圖7所示為根據車輛不同速度下的行駛數據與離線聚類質心計算得到的歐氏距離曲線，從各行駛狀態的變化趨勢來看，與圖4所示的仿真結果基本一致，都是在0～10 s，車速為40 km/h時，處于第2行駛狀態，10～20 s，車速為45 km/h時，車輛在第2和3行駛狀態之間變化，20～50 s，速度為50～60 km/h 時，車輛一直維持在第3行駛狀態，能明顯表現出隨著車速增加，車輛由安全向危險演化再向潛在危險狀態的過渡過程。

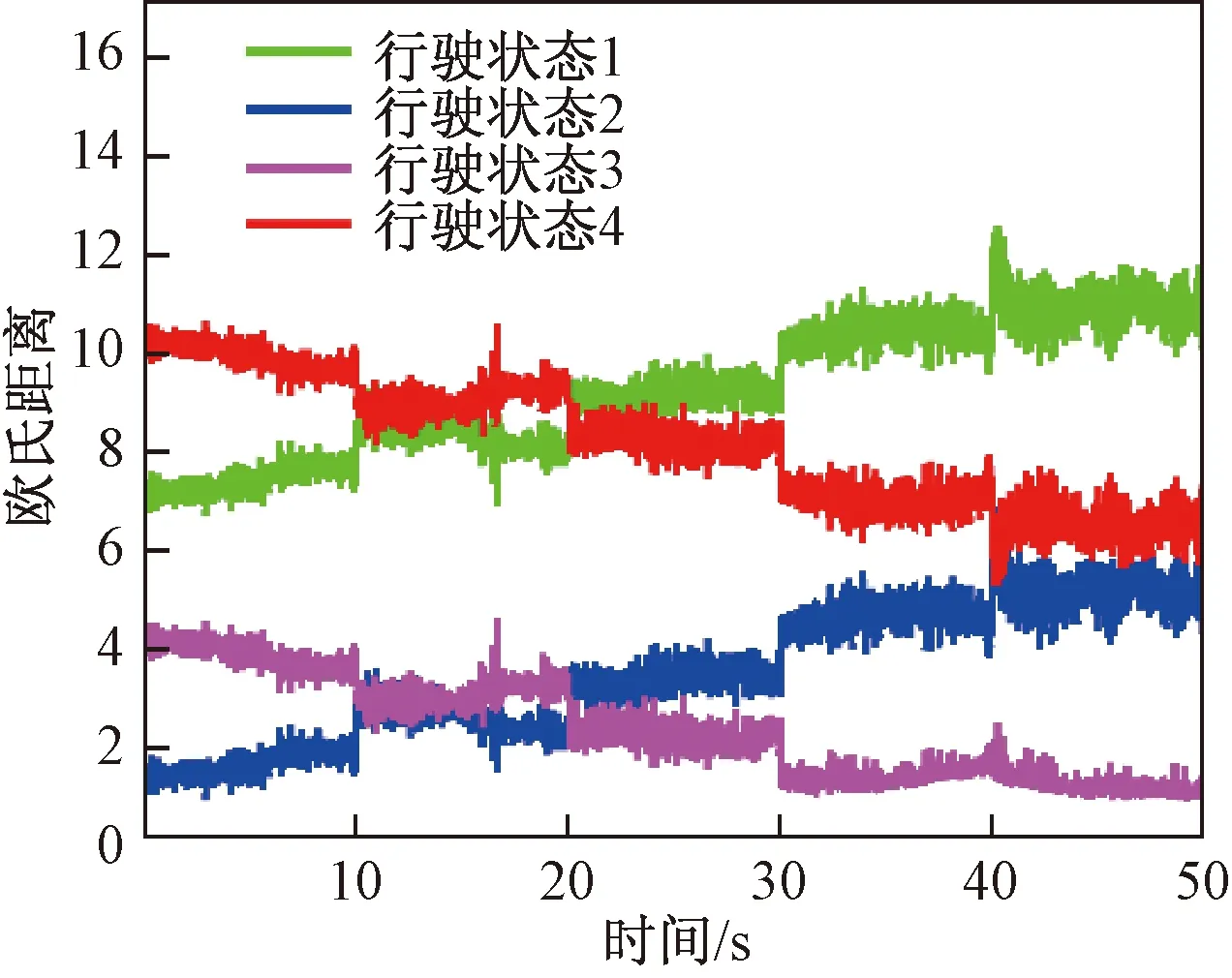
圖7 定半徑變車速試驗工況的歐氏距離

為了更清晰地表征車輛的行駛穩定性變化，繪制了不同速度下牽引車、半掛車側向加速度及橫擺角速度變化曲線，并采用12極無階巴特沃斯濾波器對原始數據進行濾波處理，如圖8所示。

圖8 牽引車和半掛車側向加速度、橫擺角速度變化曲線

圖8(a)和圖8(b)為側向加速度變化曲線，在0～10 s，也即為40 km/h時，牽引車和半掛車的側向加速度大小約為0.1g；在10～40 s，隨著速度的增加，兩者的側向加速度逐漸增大；當在40～50 s時，也即速度為60 km/h時，半掛車的側向加速度大小相較于牽引車波動較大，且有明顯的甩尾趨勢，表明此時車輛的穩定性與之前相比較差。圖8(c)和圖8(d)為橫擺角速度變化曲線，其整體變化趨勢側向加速度基本一致，都是隨著速度的增加，數值逐漸增大，車輛的穩定性逐漸變差。

圖9所示為在車輛速度為40 km/h、方向盤轉角斜階躍輸入下的行駛數據與離線聚類質心計算得到的歐氏距離曲線，從各行駛狀態的變化趨勢來看，與圖5所示的仿真結果基本一致。在0～20 s直線行駛時，處于第1行駛狀態，此時車輛為安全狀態；在20～35 s方向盤轉角勻速增加時，由第1、2行駛狀態向3、4行駛狀態變化，此時車輛逐漸由安全狀態向危險演化和潛在危險狀態過渡；在35～40 s保持方向盤轉角為180°不變時，處于第4行駛狀態，此時車輛處于潛在危險狀態。

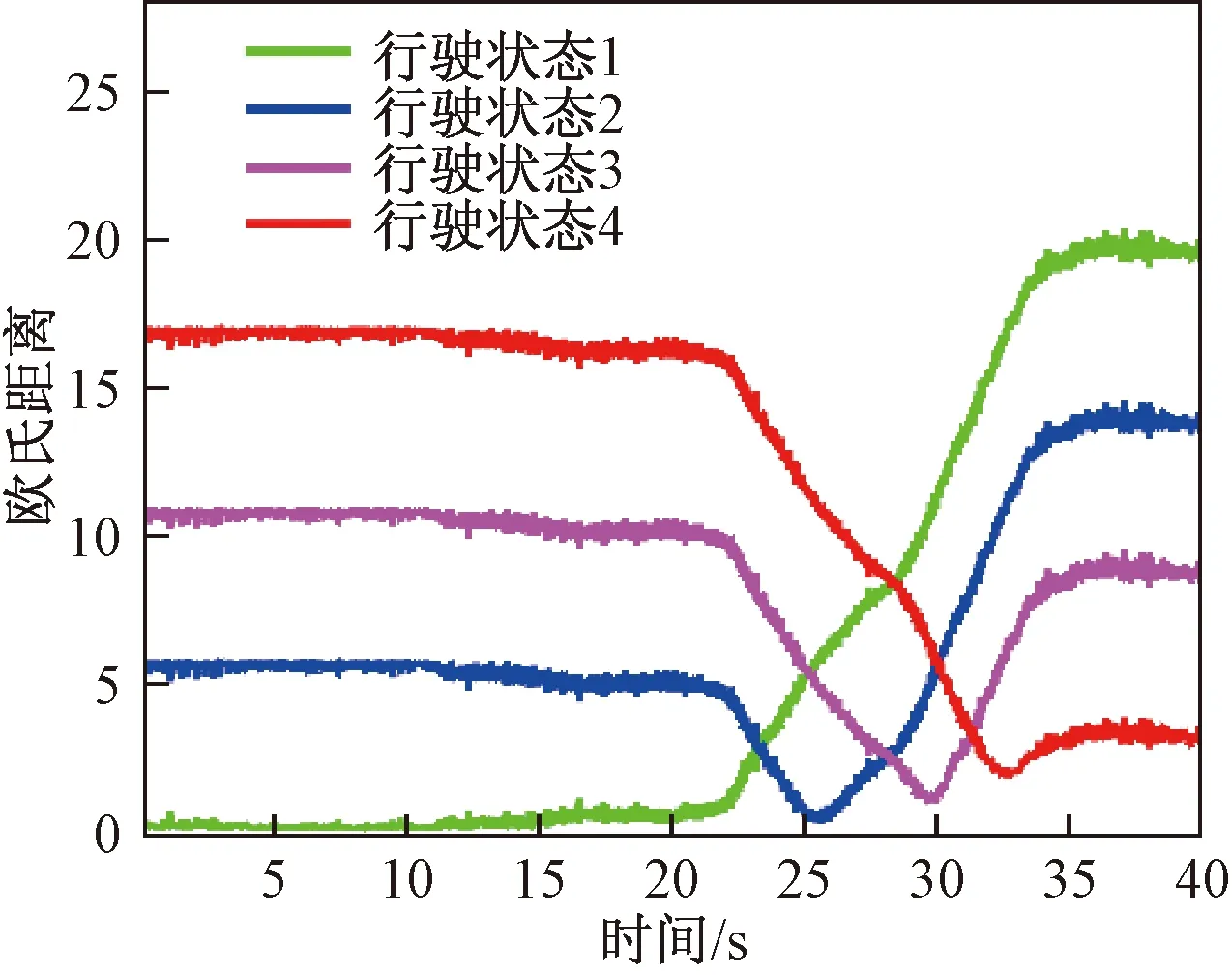
圖9 方向盤斜階躍輸入工況的歐氏距離

為了更清晰地表征車輛的行駛穩定性變化，采用與定半徑變車速試驗工況的處理方法，繪制了牽引車、半掛車側向加速度及橫擺角速度變化曲線，如圖10所示。

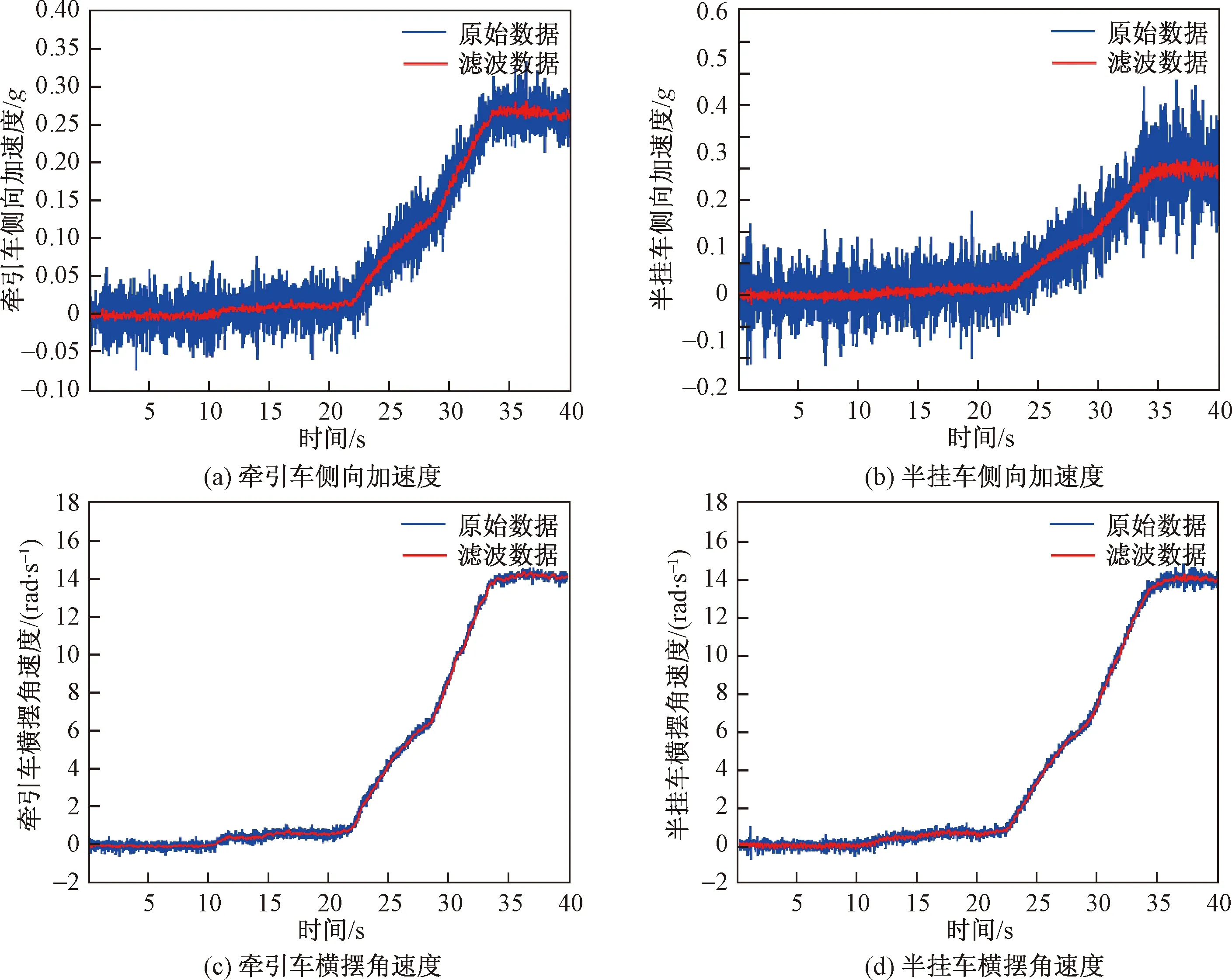
圖10 牽引車和半掛車側向加速度、橫擺角速度變化曲線

圖10(a)和圖10(b)為側向加速度變化曲線，在0～20 s，車輛以40 km/h的速度直線行駛，此時牽引車和半掛車的側向加速度大小近似為0；在20～35 s，隨著方向盤轉角的勻速增加，兩者的側向加速度逐漸增大；當在35～40 s時，也即方向盤轉角達到180°并保持不變時，半掛車的側向加速度大小相較于牽引車波動較大，表明此時車輛的穩定性與之前相比較差。圖10(c)和圖10(d)為橫擺角速度變化曲線，其整體變化趨勢與側向加速度基本一致，且都是隨著方向盤轉角的勻速增加，數值逐漸增大，車輛穩定性變差。

綜合以上兩種試驗工況的分析結果可知，根據實車采集的行駛數據和離線聚類質心進行計算歐氏距離，判定得到的行駛狀態與表征車輛行駛穩定性指標的變化基本一致。因此，從實車試驗層面，驗證了利用離線聚類結果對抗側翻穩定性試驗和方向盤斜階躍輸入工況的行駛穩定性判定也是有效的。

5 結語

選用TruckSim構建了半掛汽車列車整車模型，依據JT/T 884—2014和GB/T 38185—2019試驗標準設計仿真工況并采集了車輛行駛數據，基于Canopy-K-means算法對行駛數據進行聚類分析，并搭建了在線聯合仿真平臺和實車試驗驗證平臺，從仿真和實車試驗兩個層面驗證該算法在車輛穩定性判定領域的可行性。結果表明，采用Canopy-K-means聚類算法可以對不同行駛狀態數據進行分類，能夠獲得表征不同行駛安全特征的聚類質心，通過將定半徑變車速、方向盤斜階躍輸入兩種試驗工況采集的行駛數據和聚類質心進行歐氏距離計算，判定得到的行駛狀態與車輛所處工況下的行駛穩定性基本一致，能在一定程度上對車輛穩定性進行評價，因此可以使用表征不同行駛安全特征的聚類質心為車輛的控制和預警提供判定依據。