Hilbert空間中的廣義K-框架

陶 蕊， 李春艷

(重慶科技學院 數理與大數據學院， 重慶401331)

1 引言與預備知識

1946年，Gabor在文獻[1]中討論了信號關于基本信號的分解問題.1952年，Duffin等人[2]對Gabor的思想進行了推廣，在非調和Fourier分析中引入了框架的概念.但是，他們的工作并沒有引起太多學者們的重視. 直到1986年，Daubechies等[3]將框架理論應用到小波分析和Gabor變換中，才引發(fā)了大量學者關于框架理論的深入研究.隨后，框架理論被廣泛地應用于信號處理、圖像處理、數據壓縮以及抽樣理論等領域.

最近20年來，在Hilbert空間中，各種不同的框架概念被相繼提出，例如，一般框架，子空間框架，廣義框架和K-框架等等.關于這些框架的主要研究工作，可以參見文獻[4-9].在上述的框架概念中，Sun等[6]提出的廣義框架和Gavruta[7]提出的K-框架將算子理論與框架理論進行了結合，極大地延伸了框架理論的研究范圍.本文將在Hilbert空間中引入廣義K-框架及其對偶框架的概念.廣義K-框架是廣義框架和K-框架的一種自然推廣.利用廣義K-框架及其對偶框架可以實現對算子K的值域的重構.

本文將采用如下記號：F表示復數域或實數域，H表示定義在數域F上的可分Hilbert空間，L(H1,H2)表示從Hilbert空間H1到Hilbert空間H2上全體有界線性算子的集合.特別地，當H=H1=H2時，記為L(H). 對H中的任意兩個元素f,g，利用〈f,g〉表示f與g的內積.

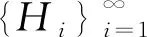
且其內積為

顯然，⊕Hi在此內積下仍然是一個Hilbert空間.特別地，對任意的i，當Hi=H時，記l2(H)=⊕Hi.

下面，先回顧廣義框架和K-框架的概念.

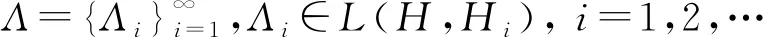
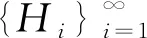
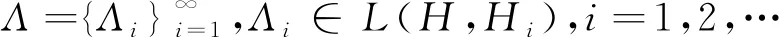
由廣義Bessel序列的定義可知RΛ是一個有界線性算子.此時，稱RΛ為Λ的解析算子.此外，通過計算可以得到算子RΛ的伴隨算子為

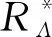
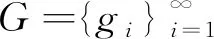
則稱G為H的K-框架.其中，常數A,B分別稱為G的框架下界和上界.

2 廣義K-框架與廣義K-原子系統

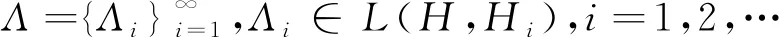
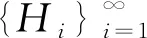
則稱Λ是緊的廣義K-框架.

由上述定義可知，廣義框架一定是一個廣義K-框架，其中K=IH，IH是定義在Hilbert空間H上的恒等算子.

在文獻[10]中，Neyshaburi等已經討論了Hilbert空間中K-框架的構造問題，給出了K-框架的一些具體例子.下面，利用K-框架構造一個廣義K-框架.

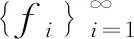
Λi∶H→Hi，Λif=〈f,fi〉ei， ?f∈H，i=1,2,…

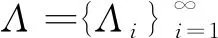
事實上，對任意f∈H，有

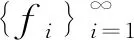
下面，給出廣義K-原子系統的概念.

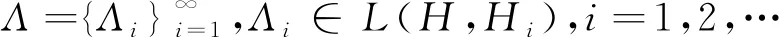
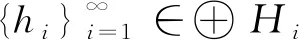
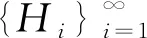
下列結論表明，可分的Hilbert空間總是存在一個關于l2(H)的廣義K-原子系統.

定理1設H是一個可分的Hilbert空間，且K∈L(H)，則H存在一個關于l2(H)的廣義K-原子系統.

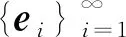
此時，令fi=Kei，且定義算子：

Λif=〈f,fi〉ei， ?f∈H.

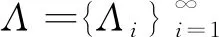
且

因此，Λ是H關于l2(H)的一個廣義K-原子系統.

注 上述定理證明過程中得到的算子序列Λ也可以成為H的一個關于l2(H)的緊的廣義K-框架. 事實上，對任意的f∈H，有

因此，Λ成為了H的一個緊的廣義K-框架.

下面，討論廣義K-原子系統與廣義K-框架之間的關系.

引理1(R.G. Douglas[11]) 設H,H1,H2為Hilbert空間，L1∈L(H1,H),L2∈L(H2,H),則下列命題等價：

(i)R(L1)?R(L2);

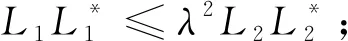
(iii) 存在有界算子C使得L1=L2C.

定理2設H,H1,H2,…,Hi,…是一列可分的Hilbert空間，且K∈L(H)，Λi∈L(H,Hi),i=1,2,…，則下列命題等價：

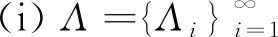
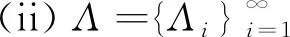
證(i) ? (ii) 設Λ是一個廣義K-原子系統，則下列算子：

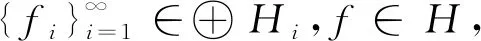
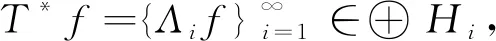
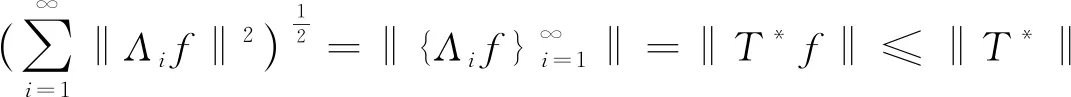
另一方面，?f∈H，有

因此，Λ是一個廣義K-框架.

其中T是Λ的合成算子.因此，有

A〈K*f,K*f〉=A〈KK*f,f〉≤〈T*f,T*f〉=〈TT*f,f〉.

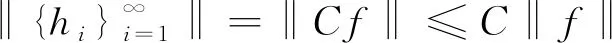
下面定理表明，任意一個廣義Bessel列，都可以成為一個廣義K-框架.

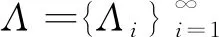
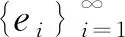
(1)

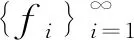
3 廣義K-框架的對偶性

為了建立基于廣義K-框架的元素重構理論，本節(jié)將討論廣義K-框架的對偶性.

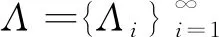
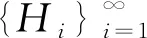
命題1如果(Γ,Λ)是一個廣義K-對偶對，則Λ是一個廣義K-框架，且Γ是一個廣義K*-框架.

證設Bessel列Λ的界為B1，Bessel列Γ的界為B2，則

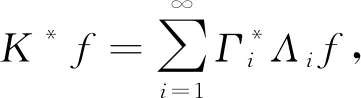
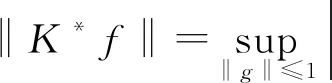
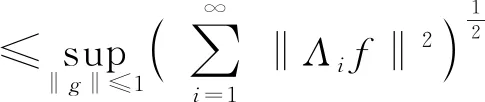
即

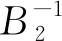
這就證明了Λ是一個廣義K-框架.

同理可證，Γ是一個廣義K*-框架.

注 由命題1的結論，也稱一個廣義K-對偶對(Γ,Λ)為一個廣義K-對偶框架對.此時，稱Γ為Λ的K*-對偶框架，稱Λ為Γ的K-對偶框架.

設Λ是一個廣義K-框架，文獻[7]中定義了算子S：

且S是一個有界線性算子，即S∈L(H)，且S是自伴的，稱算子S為Λ的框架算子.設R(K)是算子K的值域，當R(K)是閉子空間時，記P為從H到R(K)的正交投影算子.

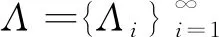
證設S為Λ的框架算子，并且記SR(K)為S在R(K)上的限制.因為算子K具有閉值域，所以,算子K的伴隨算子K*是下有界的，即存在ε>0，使得

‖K*f‖≥ε‖f‖， ?f∈H.

因為

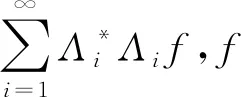
和

所以有

A‖K*f‖2≤〈Sf,f〉≤B‖f‖2.

同時有

Aε2‖f‖2≤A‖K*f‖2≤〈Sf,f〉≤‖Sf‖·‖f‖，

即Aε2‖f‖≤‖Sf‖. 這就說明算子S是一個單射且具有閉值域R(S). 又因為S是自伴算子，所以S是可逆的.

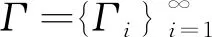
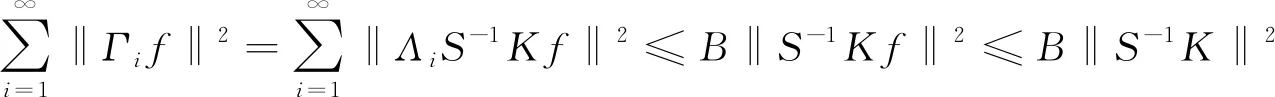
這說明Γ是一個廣義Bessel列.此外，對任意的f∈H，還有

和

因此，(Γ,Λ)是一個廣義K-對偶對，即Γ是Λ的一個K*-對偶框架.

盡管命題2表明，在算子K有閉值域的前提下，任意一個廣義K-框架的對偶框架總是存在的，但是，要精確地算出對偶框架是件非常困難的事情.早在2011年，Christensen等就在文獻[13]中對Hilbert空間中一般框架的對偶框架的近似問題進行了研究，提出了逼近對偶的概念.下面，給出廣義K-框架的逼近對偶的概念.

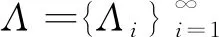
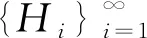
注 上述定義中，用常數ε來刻畫對偶的逼近程度.通常假設ε是一個小于1的常數，即ε<1. 此時，可以利用廣義Bessel列Λ,Γ的解析算子和合成算子定義廣義逼近K-對偶對.

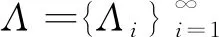
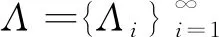
(2)

且滿足對任意的自然數n，有

(3)

則 (r,Λ)是一個廣義逼近K-對偶對.

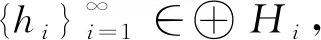
即有

當n→∞時，有

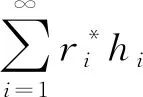
則容易驗證Tr是一個有界線性算子，且

設Rr是r的解析算子，則‖Rr‖=‖Tr‖.

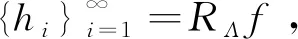
4 結 論

本文推廣了Hilbert空間中的廣義框架和K-框架的概念，引入了一種新的框架——廣義K-框架，從而給出了Hilbert空間上線性有界算子K的值域的一種新的重構方式.這種重構方式與基于一般K-框架的元素重構方式不同，它是一種基于算子序列的重構.同時，本文引入了廣義K-原子系統的概念，討論了廣義K-框架與廣義K-原子系統之間的關系.此外，為了建立基于廣義K-框架的重構理論，我們還引入了廣義K-對偶對和廣義逼近K-對偶對的概念，并給出了廣義K-對偶對存在的充分條件，研究了廣義K-對偶對和廣義逼近K-對偶對之間的關系.

致謝作者非常感謝編輯和審稿人對本文提出的修改建議，并且感謝相關文獻對本文的啟發(fā).