基于雙耦合電感高增益二次型Boost變換器

田東豪，榮德生

(遼寧工程技術大學電氣與控制工程學院，遼寧 葫蘆島 125105)

1 引言

近年來，光伏、風能等可再生能源發展迅速，其核心部件高增益DC-DC變換器備受關注。理想的Boost電路理論上在極限占空比的情況下可以達到很高的增益，如果占空比工作在接近于1的極限狀態下，輸出二極管的導通時間極短，將會導致嚴重的反向恢復和電磁干擾問題，而且由于電路寄生參數的存在，升壓增益特性受限[1-3]。因此高穩定性、高增益、高效率的DC-DC變換器受到國內外學者的廣泛關注。

傳統的Boost變換器一般采用倍壓單元[4]、開關電容(Switched Capacitor，SC)[5,6]或開關電感[7]、電壓乘法單元(Voltage Multiplier Cell,VMC)、級聯等方式提高電壓增益。針對傳統Boost變換器電壓增益受限的問題，文獻[8-14]提出了一系列基于耦合電感的高增益非隔離直流變換器，通過合理地設計耦合電感的匝比，變換器可以獲得很高的電壓增益。但存在漏感能量利用率低、開關管電壓尖峰高、漏感和開關管寄生電容諧振等問題。文獻[15]在基于耦合電感Boost變換器的基礎上通過添加無源鉗位電路和有源鉗位電路，用以吸收漏感能量，減少電路諧振現象，從而提出了一系列具有鉗位電路的耦合電感Boost變換器。但輸出二極管電壓應力高的問題沒有得到改善。文獻[16]提出了一種耦合電感高增益雙管升壓變換器，該變換器具有電壓增益大及開關管電壓電流應力低的特點，但該結構使用了兩個開關管，增加了控制的復雜度。

文獻[17]提出了單管高增益Boost變換器，所提變換器具有控制難度低、二極管電壓應力低等優點，但輸出功率較低，僅為38 W，且由于使用一個耦合電感，電壓增益受限。文獻[18]采用了雙耦合電感的結構，進一步提升電壓增益、減小二極管電壓應力，但引入了一組二極管電容無源吸收回路，增加了電路的復雜度。本文受文獻[17，18]的啟發，對其提出的拓撲進行改進，提出了一種基于雙耦合電感高增益二次型Boost變換器，在變換器輸入端采用兩級Boost，并引入兩個耦合電感倍壓單元，兩個耦合電感副邊串聯，以提高變換器的電壓增益。與輸出端共用二極管和電容實現無源吸收回路，抑制了開關管電壓尖峰，同時提高了電路的功率密度。文中詳細分析了所提變換器的工作原理和工作特性，并制作了一臺180 W、18 V/180 V的實驗樣機，驗證了理論分析的正確性。

2 工作原理分析

2.1 電路拓撲

圖1(a)為雙耦合電感Boost高增益DC-DC變換器拓撲，電路由輸入電源Vin，耦合電感L1、L2，電容C1、Co1、Co2、Co3,二極管VD1、VD2、VDo1、VDo2和VDo組成。圖1(b)為拓撲等效電路，耦合電感L1、L2等效為由勵磁電感Lm1、Lm2，漏感Lk1、Lk2和匝比為np1:ns1、np1:ns2的理想變壓器構成，假設n=ns1/np1=ns2/np2。輸出二極管VDo和輸出電容Co1構成無源吸收電路，當開關管S關斷后，耦合電感L1原邊的漏感Lk1通過VD2向電容C1釋放能量；耦合電感L2原邊的漏感Lk2通過二極管VD2向電容Co1釋放能量，從而提升了漏感能量的利用率。VDo、VDo1、VDo2為輸出二極管，Co1、Co2、Co為輸出濾波電容，C1為中間儲能電容，Ro為負載電阻。為簡化分析，提出如下假設：

(1)開關管S和二極管VD1、VD2、VDo1、VDo2、VDo為理想器件。

(2)電容C1、Co1、Co2、Co3的容值足夠大，其端電壓保持恒定。

(3)設兩個耦合電感的耦合系數k相等，并且設k=Lm/(Lm+Lk)。

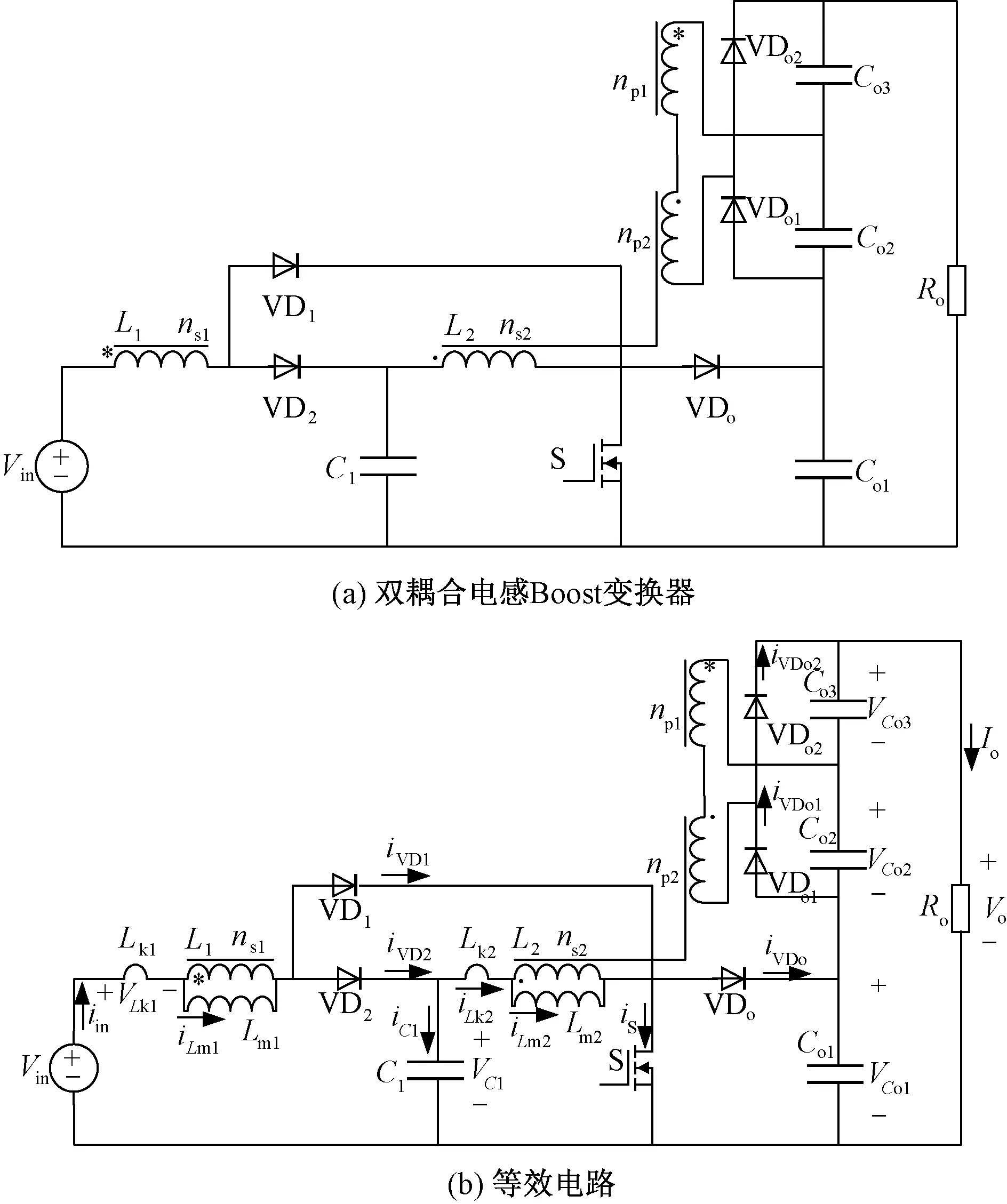
圖1 所提變換器拓撲結構Fig.1 Proposed converter topology

2.2 連續工作模態分析

假設勵磁電感Lm1和勵磁電感Lm2的電流均連續，即工作在連續工作模式(Continuous Conduction Mode,CCM)。如圖2為該變換器工作在CCM下的關鍵工作波形，在一個開關周期內，該變換器存在如圖3所示的5種工作模態。

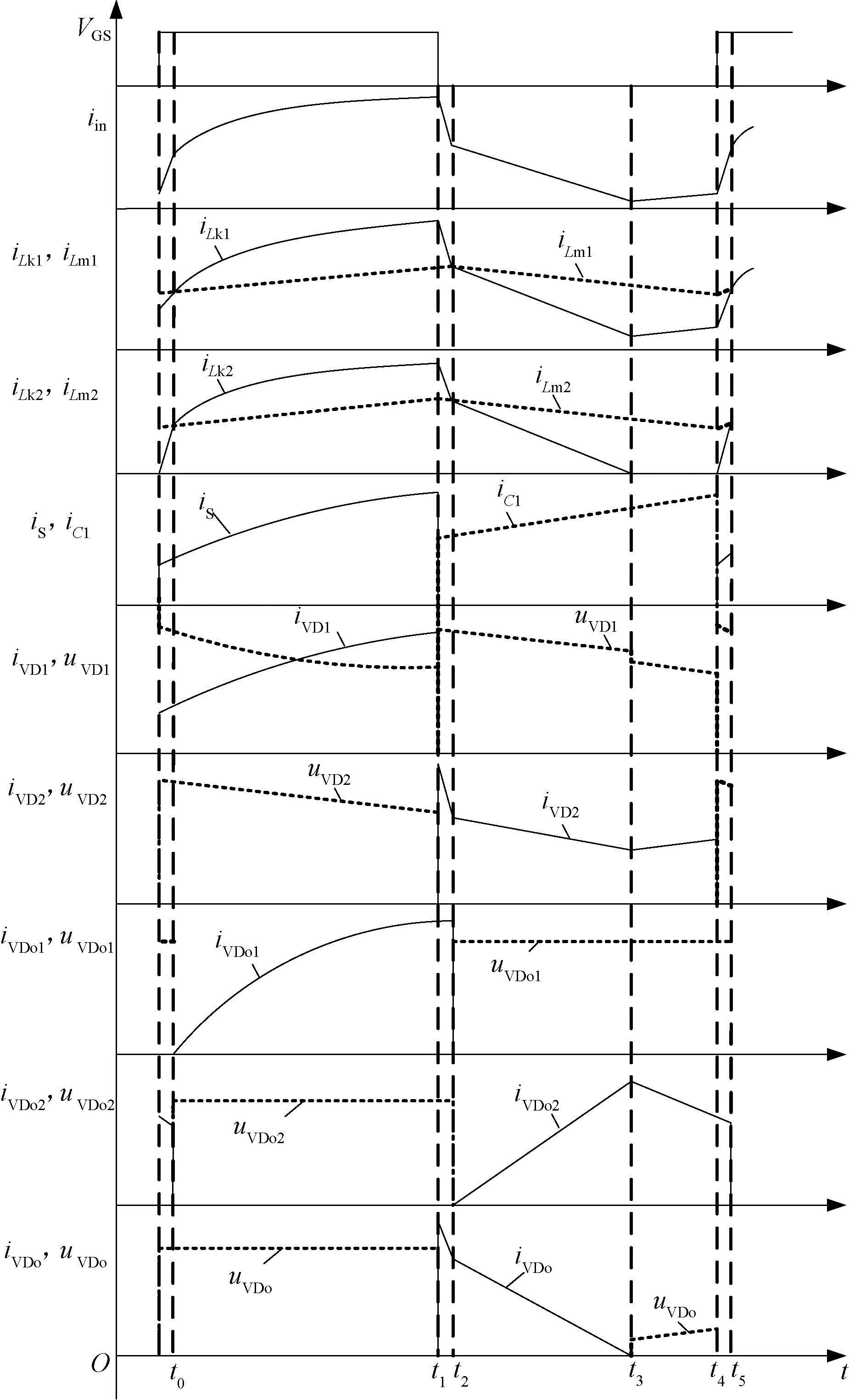
圖2 變換器的主要波形圖(CCM)Fig.2 Main waveforms of converter (CCM)

模態Ⅰ[t0～t1]：如圖3(a)所示，開關管S處于導通狀態，二極管VD1和VDo1因承受正向壓降導通，二極管VD2、VDo2和輸出二極管VDo關斷。輸入電壓作用在勵磁電感Lm1上，勵磁電感Lm1儲能，勵磁電感電流iLm1線性上升。電容C1通過開關管S給勵磁電感Lm2儲能，電感電流iLm2線性上升。耦合電感L1的漏感電流即輸入電流線性上升。耦合電感副邊串聯給輸出電容Co2充電，輸出電容Co1、Co2和Co3串聯給負載供電。當開關管S關斷時，此模態結束。在此階段，根據基爾霍夫電壓定律，iLm1、iLm2和iin可以表示為：

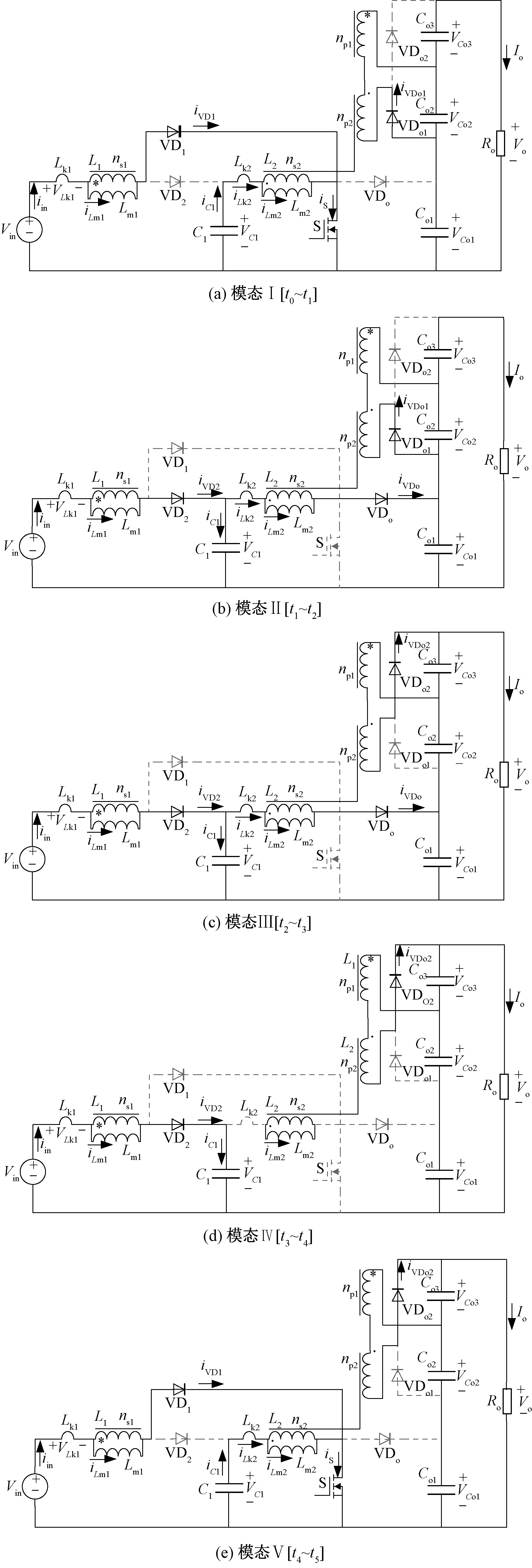
圖3 所提變換器各個工作模態等效電路圖(CCM)Fig.3 Equivalent circuits of switching modes(CCM)

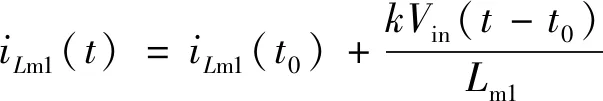
(1)

(2)

(3)

模態Ⅱ[t1～t2]：如圖3(b)所示，t1時刻，二極管VD1關斷。為提供耦合電感L1原邊線圈的電流通路，二極管VD2和VDo因承受正向電壓而開通，二極管VDo1和VDo2維持上一模態狀態不變。輸入電壓Vin、勵磁電感Lm1和漏感Lk1串聯給電容C1充電，漏感Lk2的能量釋放給輸出電容Co1，耦合電感副邊串聯繼續給輸出電容Co2充電。由于此模態過程極短，可認為勵磁電感電流基本不變。二極管VDo1承受反向電壓關斷時，此模態結束。

模態Ⅲ[t2～t3]：如圖3(c)所示，開關管S保持關斷，二極管VDo1關斷，為提供耦合電感副邊線圈的電流通路，二極管VDo2因承受正向電壓而導通；二極管VD1和VD2維持上一模態狀態不變。輸入電壓Vin和耦合電感L1的原邊串聯給中間電容C1充電。輸出二極管VDo導通，輸入電源Vin、耦合電感L1原邊和耦合電感L2原邊經過VDo給輸出電容Co1充電。同時漏感電流iLk1向C1釋放，iLk2向Co1釋放，輸出電容Co3通過勵磁電感副邊儲能。勵磁電感電流iLm1和iLm2線性下降。輸出電容Co1、Co2和Co3串聯為輸出負載供電。輸出二極管VDo電流下降，當iVDo=0時，VDo自然關斷，此模態結束。勵磁電感Lm1和Lm2的電流表示如下：

(4)

(5)

模態Ⅳ[t3～t4]：如圖3(d)所示，t3時刻，二極管VDo實現零電流關斷，其余二極管維持上一模態狀態不變。漏感Lk2的能量釋放完畢，勵磁電感Lm2能量通過耦合電感傳遞到副邊，勵磁電感電流iLm1和iLm2繼續線性下降。輸入電源和耦合電感L1原邊串聯給電容C1充電，耦合電感副邊串聯給輸出電容Co3充電。輸出電容Co1、Co2和Co3串聯為輸出負載供電。直到下一個開關周期驅動脈沖的到來，此模態結束。

模態Ⅴ[t4～t5]：如圖3(e)所示，t4時刻，驅動信號VGS加在開關管S的兩端，開關管S導通。二極管VD1和VDo2因承受正向壓降而導通。二極管VD2、VDo1和VDo關斷。當開關管S導通時，輸入電壓作用在耦合電感L1原邊，電容C1釋放能量給耦合電感L2原邊。勵磁電感電流iLm1和iLm2線性上升，副邊通過二極管VDo2給輸出電容Co3充電，輸出電容Co1、Co2和Co3串聯給負載Ro提供能量，當二極管VDo2因承受反向電壓而關斷時，此模態結束。

2.3 非連續工作模態分析

當勵磁電感Lm1電流連續，Lm2的電流斷續，電路工作在連續-非連續工作模式(Continuous Conduction Mode-Discontinuous Conduction Mode,CCM-DCM)模式下；當勵磁電感Lm1和Lm2的電流均斷續，電路工作在DCM-DCM下。在一個開關周期內，所提變換器在CCM-DCM下存在5個工作模態，圖4為變換器工作的主要波形，各個模態的等效電路如圖5(a)～圖5(e)所示。

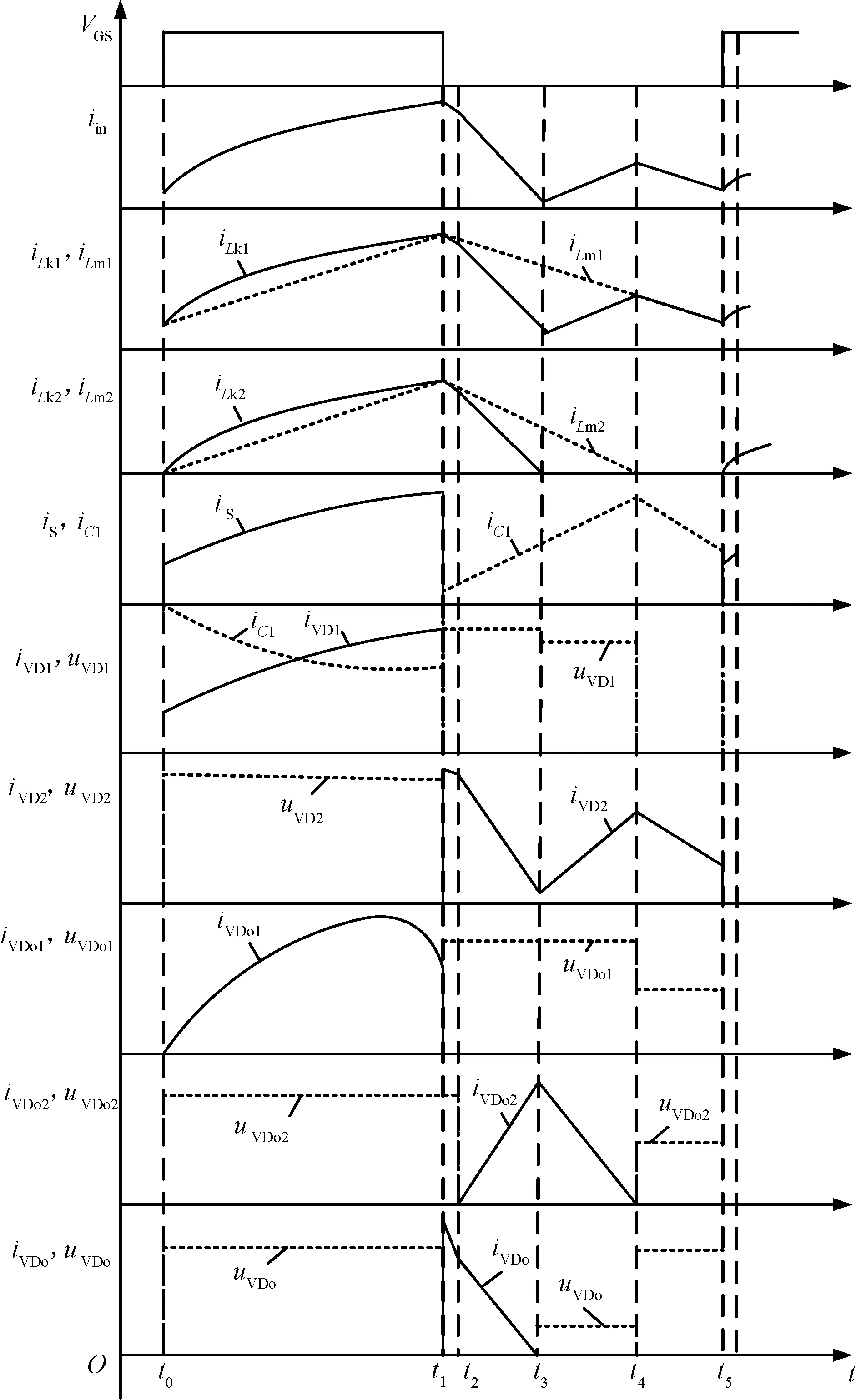
圖4 變換器的主要波形圖(DCM)Fig.4 Main waveforms of converter (DCM)

模態Ⅰ[t0～t1]：如圖5(a)所示，在t0時刻，開關管S開通，二極管VD1和VDo1導通，二極管VD2和VDo2關斷，輸出二極管VDo關斷。電源電壓加在耦合電感L1原邊Lm1上，耦合電感L2原邊電壓VLm2等于C1兩端電壓。電流iLm1和iLm2線性上升。耦合電感副邊串聯給Co2充電。當開關管S關斷時，此模態結束。

模態Ⅱ[t1～t2]：如圖5(b)所示，在t1時刻，開關管S關斷，二極管VDo、VD2和VDo1導通，二極管VD1和VDo2關斷。漏感電流和勵磁電感電流緩慢下降。耦合電感副邊給電容Co2充電。電容C1和Co1吸收漏感能量。負載能量由輸出電容Co1、Co2和Co3串聯提供。此模態持續時間極短，當二極管VDo1關斷，二極管VDo2導通時，此模態結束。

模態Ⅲ[t2～t3]：如圖5(c)所示，開關管S保續關斷，二極管VDo2導通，二極管VDo1關斷，其他二極管狀態與上一模態相似。耦合電感L1和L2原邊漏感電流快速下降，漏感能量繼續被電容C1和Co1吸收，耦合電感副邊串聯給輸出電容Co3儲能，原邊勵磁電流iLm1和iLm2線性下降，當耦合電感L2原邊漏感電流iLk2降至零時，此模態結束。

模態Ⅳ[t3～t4]：如圖5(d)所示，在t3時刻，開關管保持關斷，漏感Lk2的能量已經釋放完畢。二極管VD2和VDo2保持導通，二極管VD1、VDo1和VDo截止。輸入電流即勵磁電感Lm1的電流線性下降，且電壓為k(Vin-VC1)，電容Co3繼續充電儲能。當勵磁電感Lm2中的電流iLm2為零時，此模態結束。

模態Ⅴ[t4～t5]：如圖5(e)所示，在這個模態中，勵磁電感Lm2電流為零，耦合電感L1的漏感電流iLk1和勵磁電感電流iLm1相等。二極管VD2導通，開關管S和二極管VD1、VDo、VDo1、VDo2均關斷，VD2中的電流線性下降。電容C1充電儲能。負載能量由輸出電容Co1、Co2和Co3串聯提供。當開關管S導通時，此模態結束，下一周期開始。

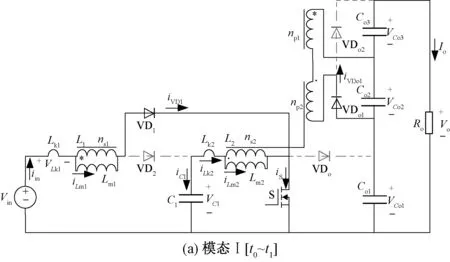
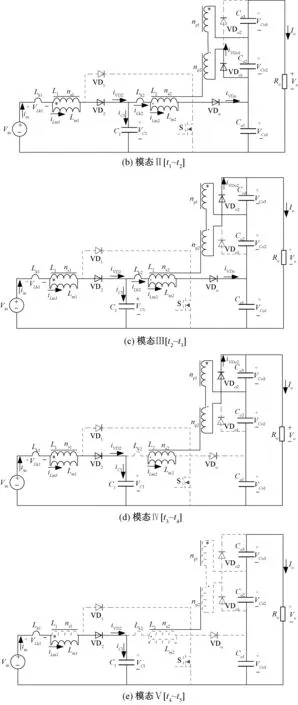
圖5 所提變換器各個工作模態等效電路圖(DCM)Fig.5 Equivalent circuits of switching modes(DCM)

3 變換器穩態性能分析

3.1 CCM工作模態模式

為了便于穩態分析，忽略過渡模態Ⅱ和Ⅴ，僅討論分析模態Ⅰ、模態Ⅲ和模態Ⅳ。假設耦合電感的耦合系數相同且為k，耦合系數k為：

(6)

假設耦合電感的匝比相同且為n，匝比n可以表示為：

(7)

當變換器工作在模態Ⅰ時，根據圖3(a)，有：

(8)

(9)

(10)

當變換器工作在模態Ⅲ時，由圖3(c)有：

(11)

(12)

(13)

當變換器工作在模態Ⅳ時，由圖3(d)有：

(14)

(15)

對耦合電感L1、L1原邊勵磁電感Lm1和勵磁電感Lm2使用伏秒平衡原理，有：

(16)

(17)

結合式(8)、式(11)、式(14)和式(16)得到電容C1的電壓為：

(18)

根據式(10)可以得到Co2的電壓為：

(19)

由式(9)、式(12)、式(14)、式(15)和式(17)可以得到Co1的電壓為：

(20)

根據式(13)可以得到Co3的電壓為：

(21)

結合式(19)～式(21)可以得到輸出電壓Vo的表達式為：

(22)

根據式(22)可以得到變換器工作在CCM下的電壓增益表達式為：

(23)

根據式(23)可知，變換器的電壓增益和耦合電感的匝比n、耦合系數k有關。圖6是變換器電壓增益和耦合電感匝比n、耦合系數k的關系曲線。從圖中可以看出，耦合電感匝比n越大，變換器的電壓增益越高；而隨著兩耦合電感漏感的增加，所提變換器的電壓增益有一定的減小，故在實際設計中，應盡可能地使耦合電感緊耦合。

為了簡化分析，令耦合電感耦合系數k=1，忽略漏感對變換器的影響。此時變換器的電壓增益為：

(24)

開關管S的電壓應力為：

(25)

二極管VD1和VD2的電壓應力為：

(26)

(27)

二極管VDo的電壓應力為：

(28)

二極管VDo1和VDo2的電壓應力為：

(29)

3.2 DCM臨界條件

假設勵磁電感Lm1的電流連續，勵磁電感Lm2電流斷續，即工作在CCM-DCM下。并假設所提變換器為理想變換器，有：

VoIo=VinIin

(30)

對于勵磁電感Lm1工作在CCM下需滿足以下條件：

2ILm1>ΔiLm1

(31)

式中，ILm1為勵磁電感Lm1的電流平均值；ΔiLm1為勵磁電感Lm1的電流紋波。

ILm1可以表示為：

(32)

勵磁電感Lm1的電流紋波可以表示為：

(33)

假設等效電感時間常數τLm1表示為：

(34)

由式(30)～式(34)可以得到勵磁電感Lm1電流連續的臨界條件為：

(35)

當τ<τLm1時，變換器工作在CCM-DCM模式。

假設模態Ⅲ持續的時間為DX，模態Ⅳ持續的時間為DY。在每一個開關周期中，二極管VDo的平均值可以表示為：

(36)

二極管VDo2的電流平均值可以表示為：

(37)

假設輸出電容Co1、Co2、Co3足夠大，則可以認為在變換器穩定工作時流過輸出電容的電流為零，所以可近似認為IVDo1、IVDo2、IVDo三者電流相等。根據式(36)和式(37)可以得到：

(38)

(39)

設開關管的開關頻率為fs，勵磁電感Lm2的時間常數τLm2可以表示為：

(40)

圖7展示了當耦合電感匝比n=1時，所提變換器勵磁電感Lm1和Lm2的電流臨界連續的時間常數與占空比D的關系。當τ>τLm2時，變換器工作在CCM-CCM模式；當τLm1<τ<τLm2時，變換器工作在CCM-DCM模式；當τ<τLm1時，變換器工作在DCM-DCM模式，即流過勵磁電感Lm1和Lm2的電流斷續。

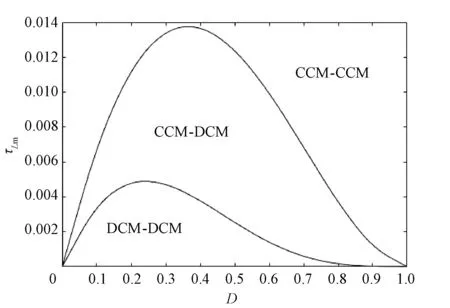
圖7 臨界等效電感時間常數與占空比D的關系曲線圖Fig.7 Relationship between critical parallel equivalent inductance time constant and duty cycle D

3.3 變換器性能對比

將本文所提變換器與文獻[17-19]所提變換器的各項性能指標進行對比，各項參數對比見表1。本文所提變換器當匝比n=1，k=1時，開關管S的電壓應力僅為輸出電壓的2/5，具有開關管電壓應力低的優點。

表1 不同變換器性能參數Tab.1 Different converter performance parameters

在匝比n固定的情況下，給定耦合電感匝比n=1，變換器的增益對比曲線如圖8所示。從圖8中可以看出，當n和k固定的情況下，所提變換器的電壓增益明顯更高。

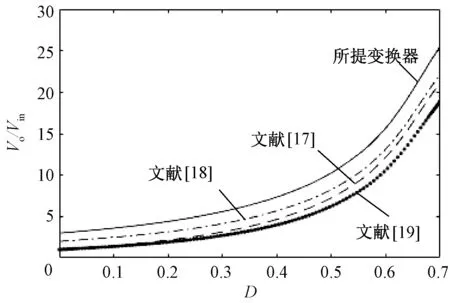
圖8 變換器增益對比曲線Fig.8 Converter gain comparison curves

圖9為變換器開關管電壓應力對比曲線，盡管在占空比大于0.4的時候文獻[19]比所提變換器的開關管電壓應力小，但在相同增益的情況下，所提變換器仍比文獻[19]開關管電壓應力小。

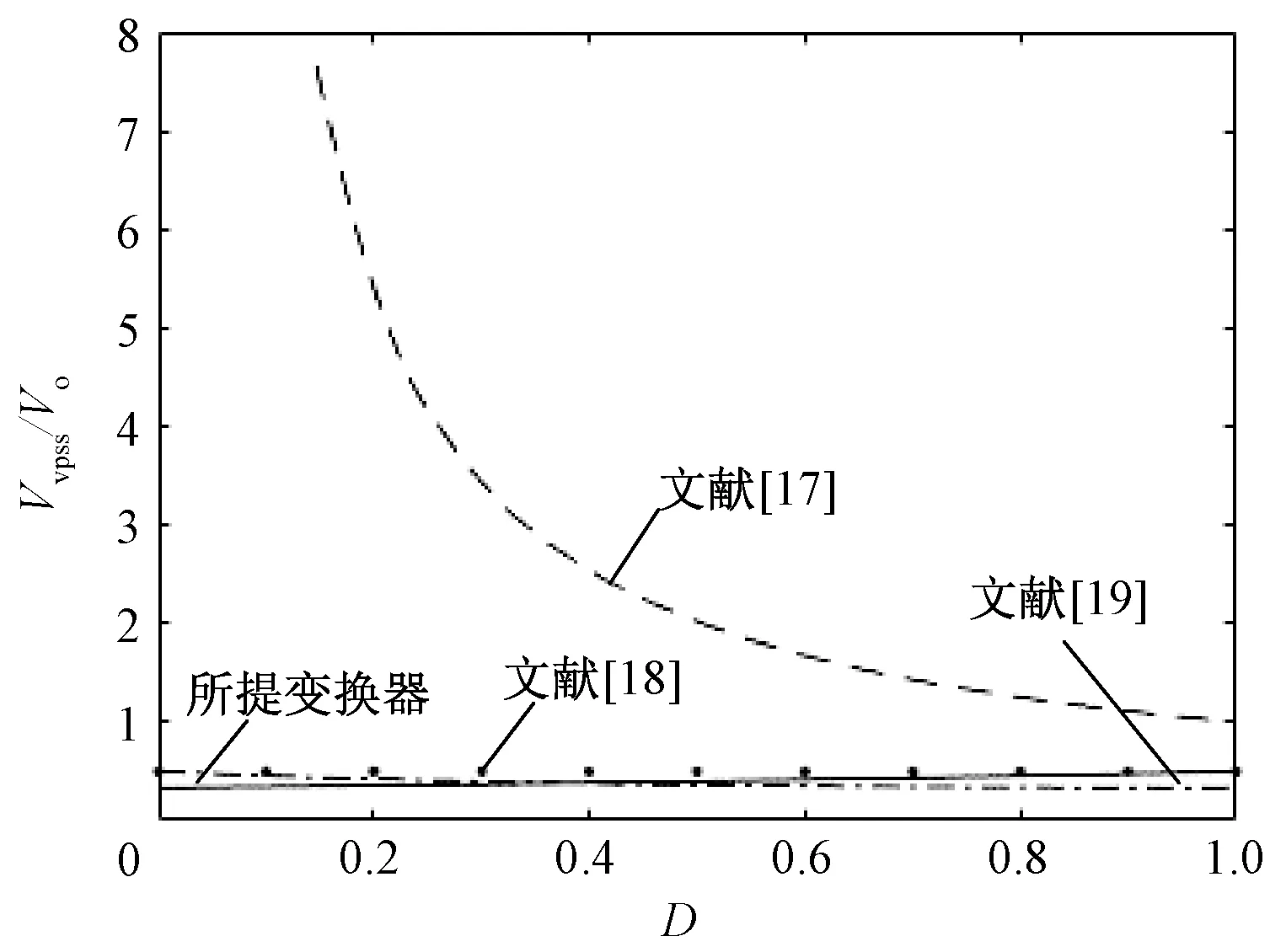
圖9 變換器開關管電壓應力對比曲線Fig.9 Comparative converter switch voltage stress curves

4 實驗結果與分析

為驗證本文所提出的高增益DC-DC變換器原理的正確性，制作了一臺試驗樣機以驗證理論分析的正確性，主電路的主要參數見表2。實驗樣機如圖10所示。

表2 主電路參數Tab.2 Main circuit parameters

圖10 試驗樣機Fig.10 Experimental prototype

圖11為變換器的輸入輸出電壓波形，可以看出，變換器實現了輸入18 V，輸出180 V的高增益變換。圖12為開關管S的電流波形及電壓波形圖。圖13為兩個耦合電感漏感Lk1和Lk2的電流波形圖。

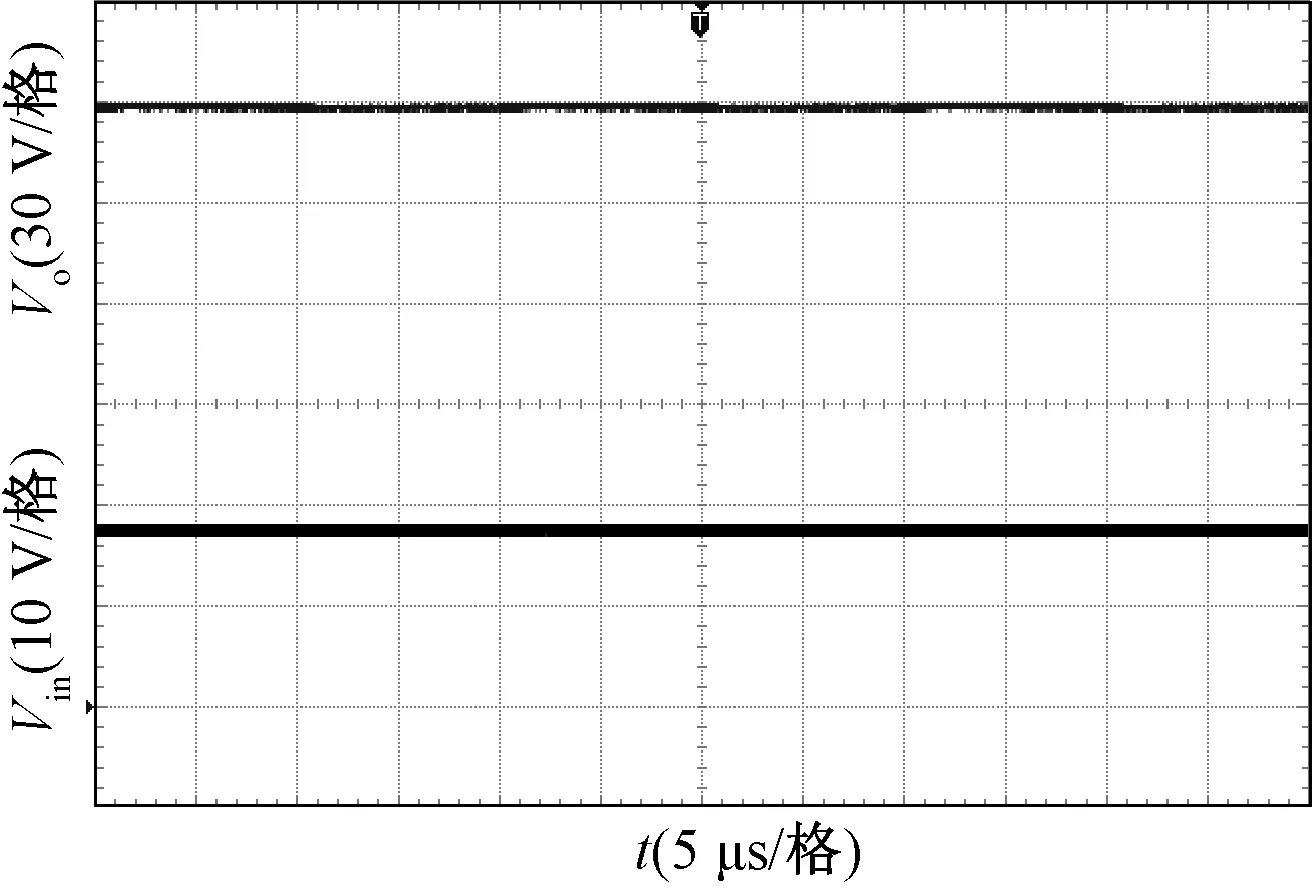
圖11 Vin,Vo波形Fig.11 Waveforms of Vin and Vo

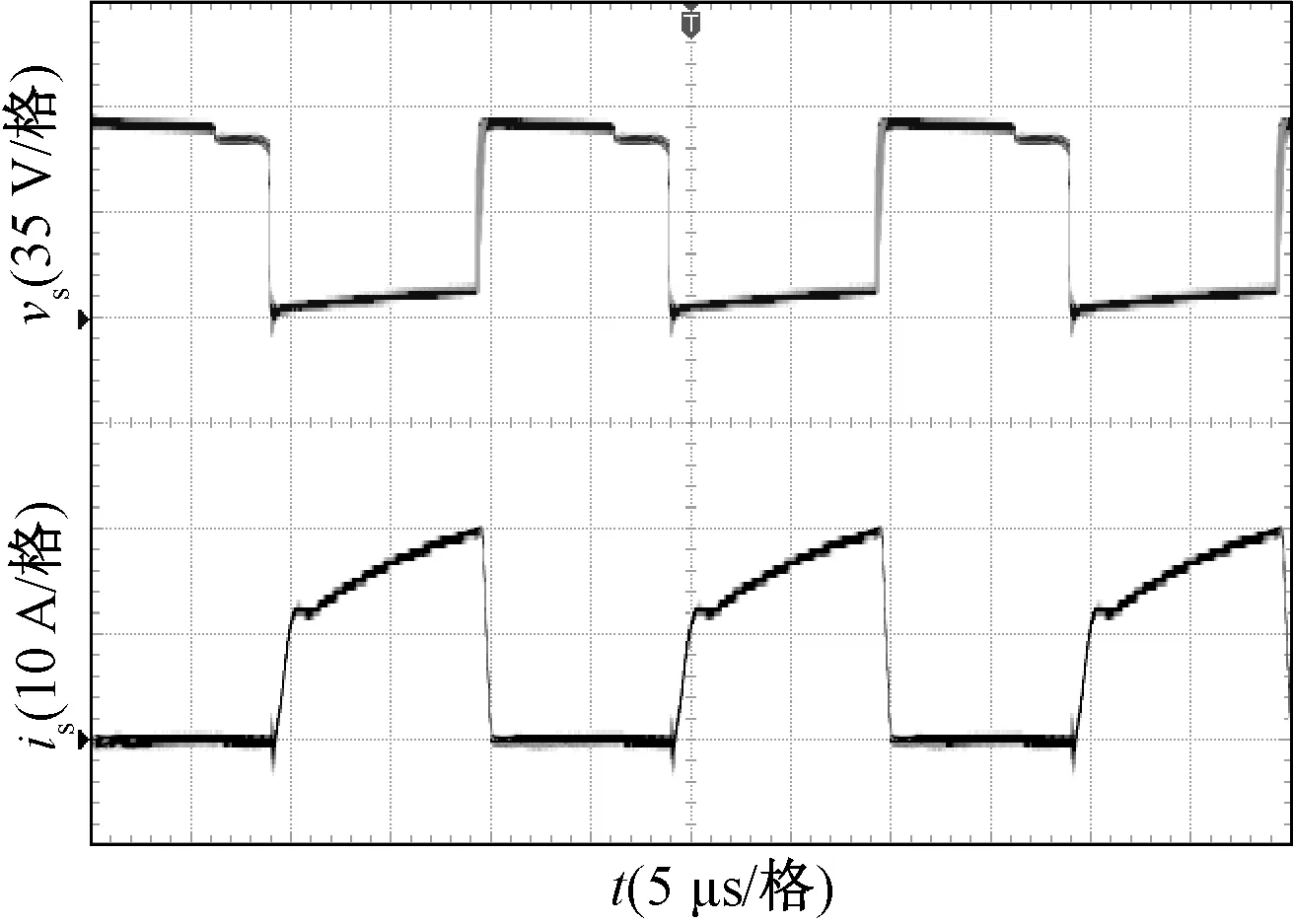
圖12 開關管S的電流和電壓波形Fig.12 Waveforms of us and is

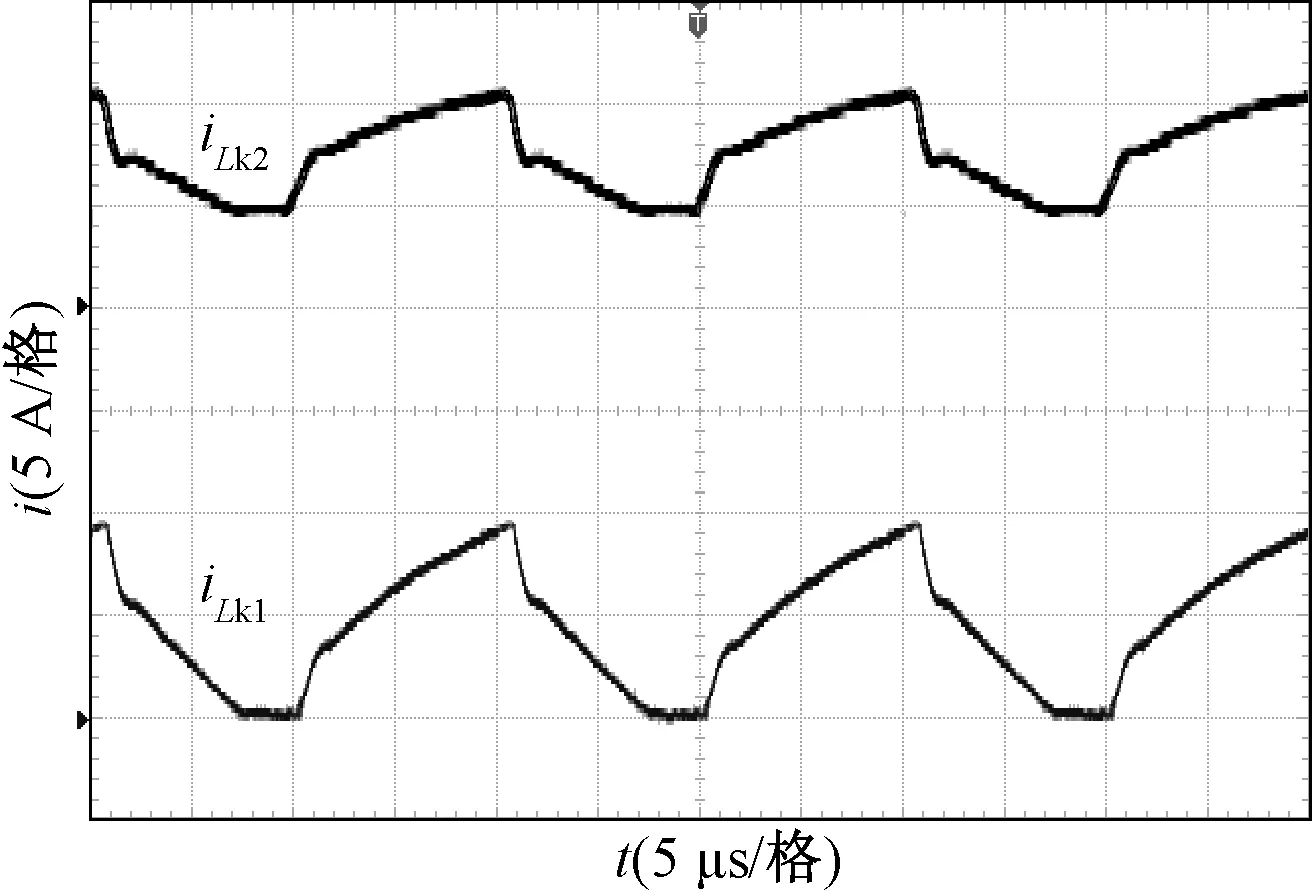
圖13 Lk1和Lk2的電流波形圖Fig.13 Waveforms of iLk1 and iLk2

圖14為輸出二極管VDo電流和電壓波形圖，VDo的電壓約為80 V低于輸出電壓。圖15和圖16分別為二極管VD1和VD2的電流和電壓波形圖，兩個二極管的電壓約為40 V。圖17和圖18分別為輸出二極管VDo1和VDo2的電流和電壓波形圖，兩個輸出二極管的電壓約為90 V，電流約為3 A。

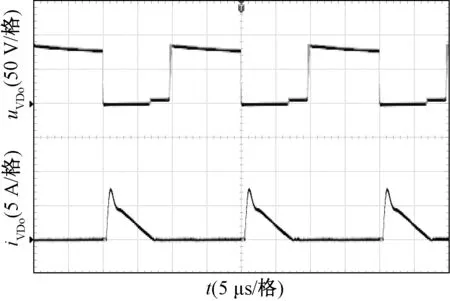
圖14 二極管VDo的電壓和電流波形Fig.14 Waveforms of uVDo and iVDo

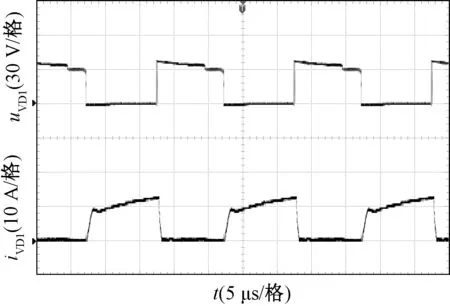
圖15 二極管VD1的電壓和電流波形Fig.15 Waveforms of uVD1 and iVD1

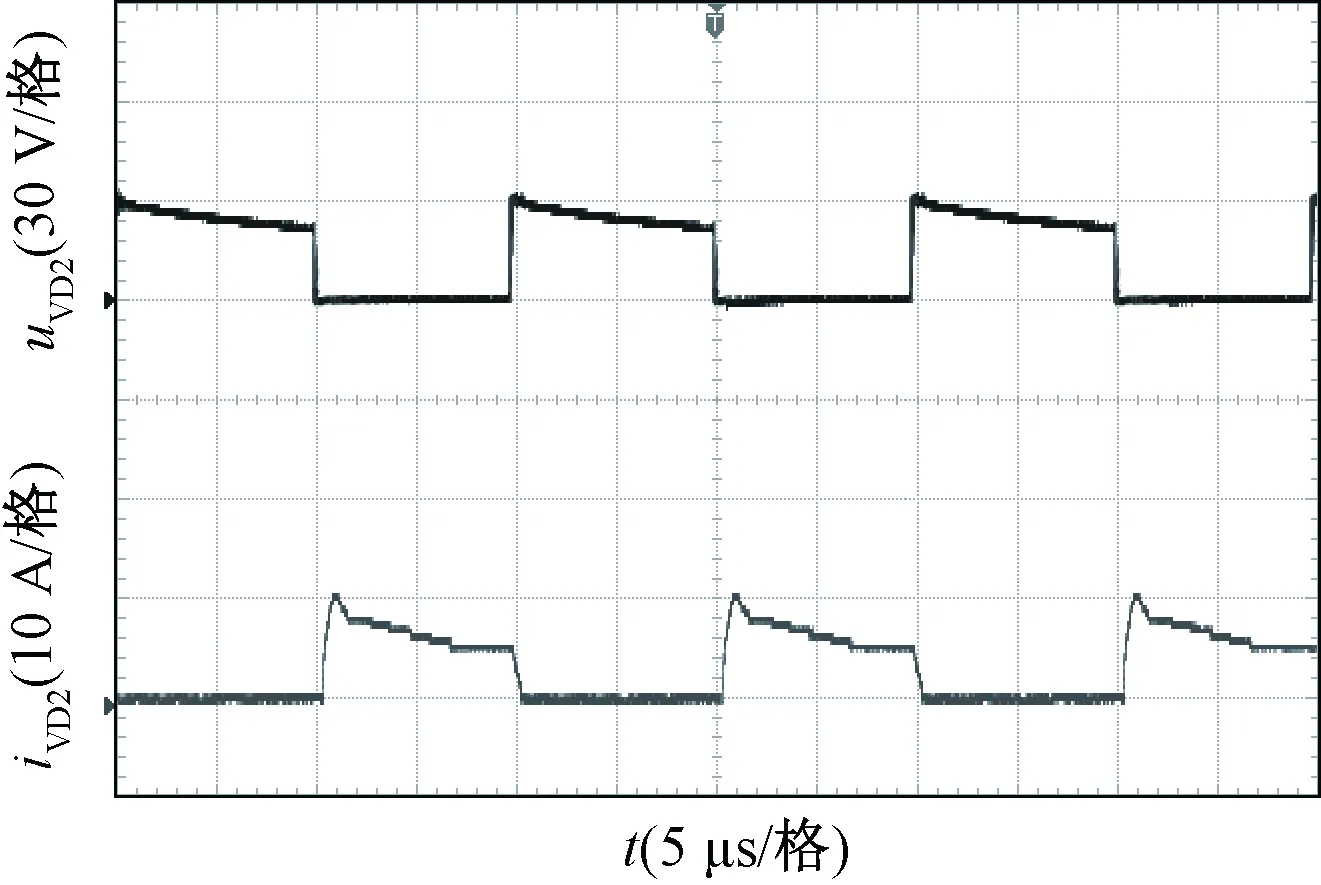
圖16 二極管VD2的電壓和電流波形Fig.16 Waveforms of uVD2 and iVD2

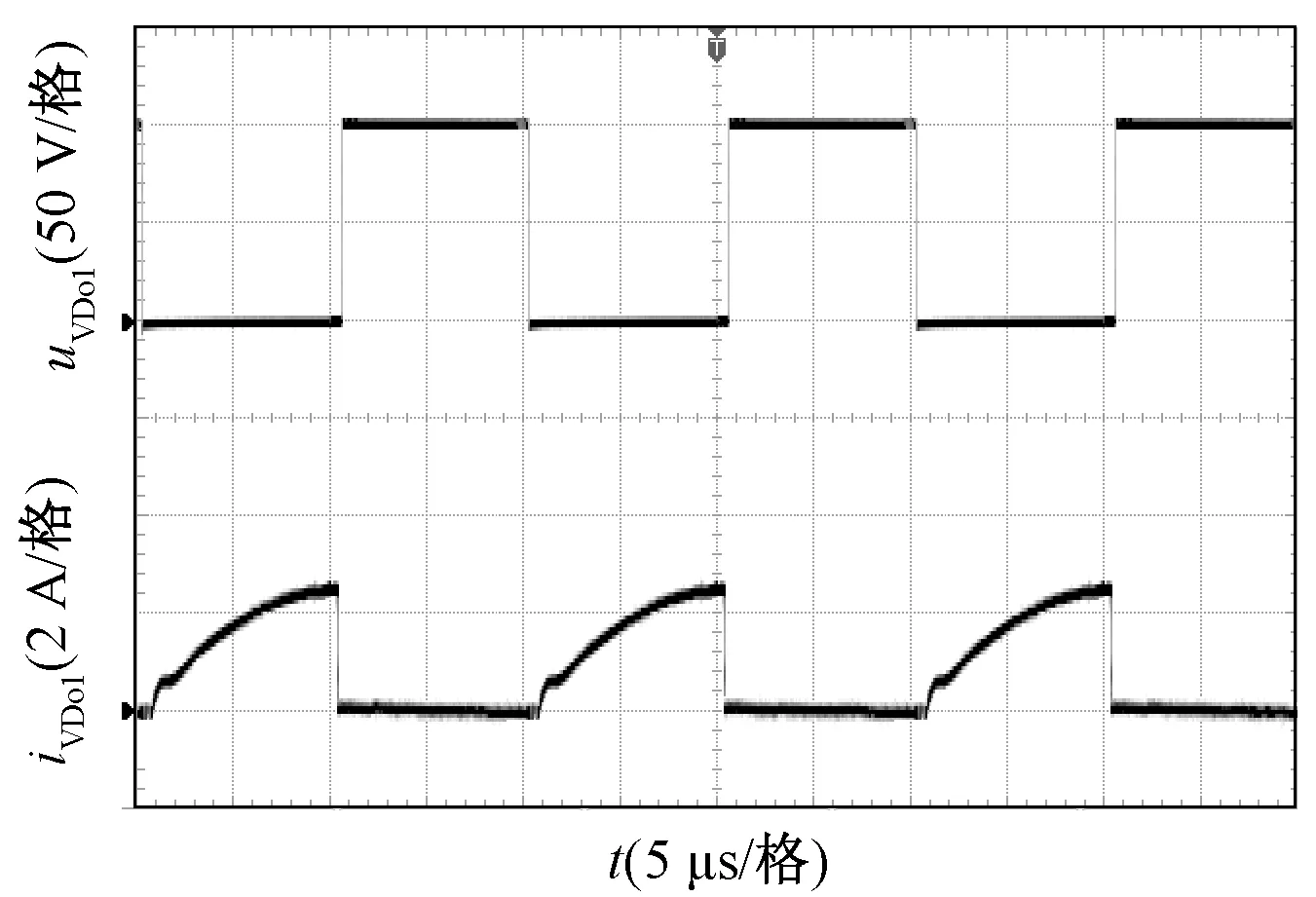
圖17 二極管VDo1的電壓和電流波形Fig.17 Waveforms of uVDo1 and iVDo1

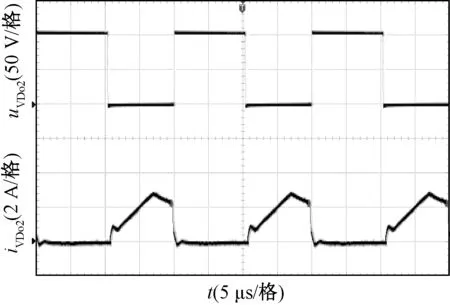
圖18 二極管VDo2的電壓和電流波形Fig.18 Waveforms of uVDo2 and iVDo2

為進一步證明所提變換器高增益和二極管低電壓應力等特點，將輸入電壓設置為12 V，測得其耦合電感漏感電流波形、開關管電壓波形、二極管VDo1、VD1、VD2電壓和輸入輸出波形，如圖19所示。從圖19中可進一步驗證本文所提拓撲理論的正確性。

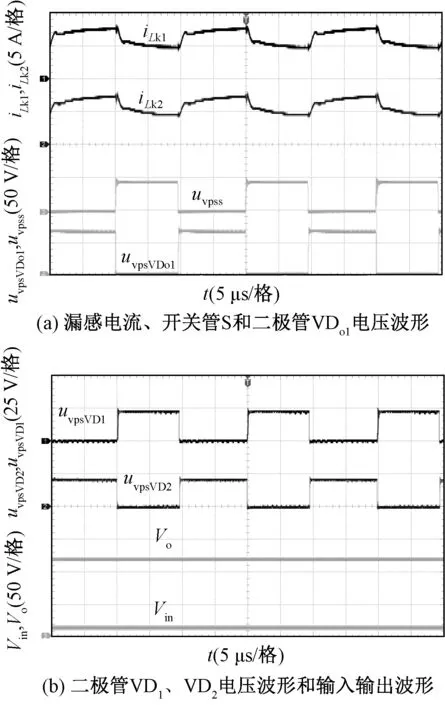
圖19 Vin=12 V時關鍵波形圖Fig.19 Waveforms of Vin=12 V

圖20為所提變換器在180 V輸出不變的情況下，效率隨輸出功率變化的曲線。當輸出功率為90 W時，輸出功率最大，最大效率為94%，在額定功率180 W條件下效率可達92.5%。

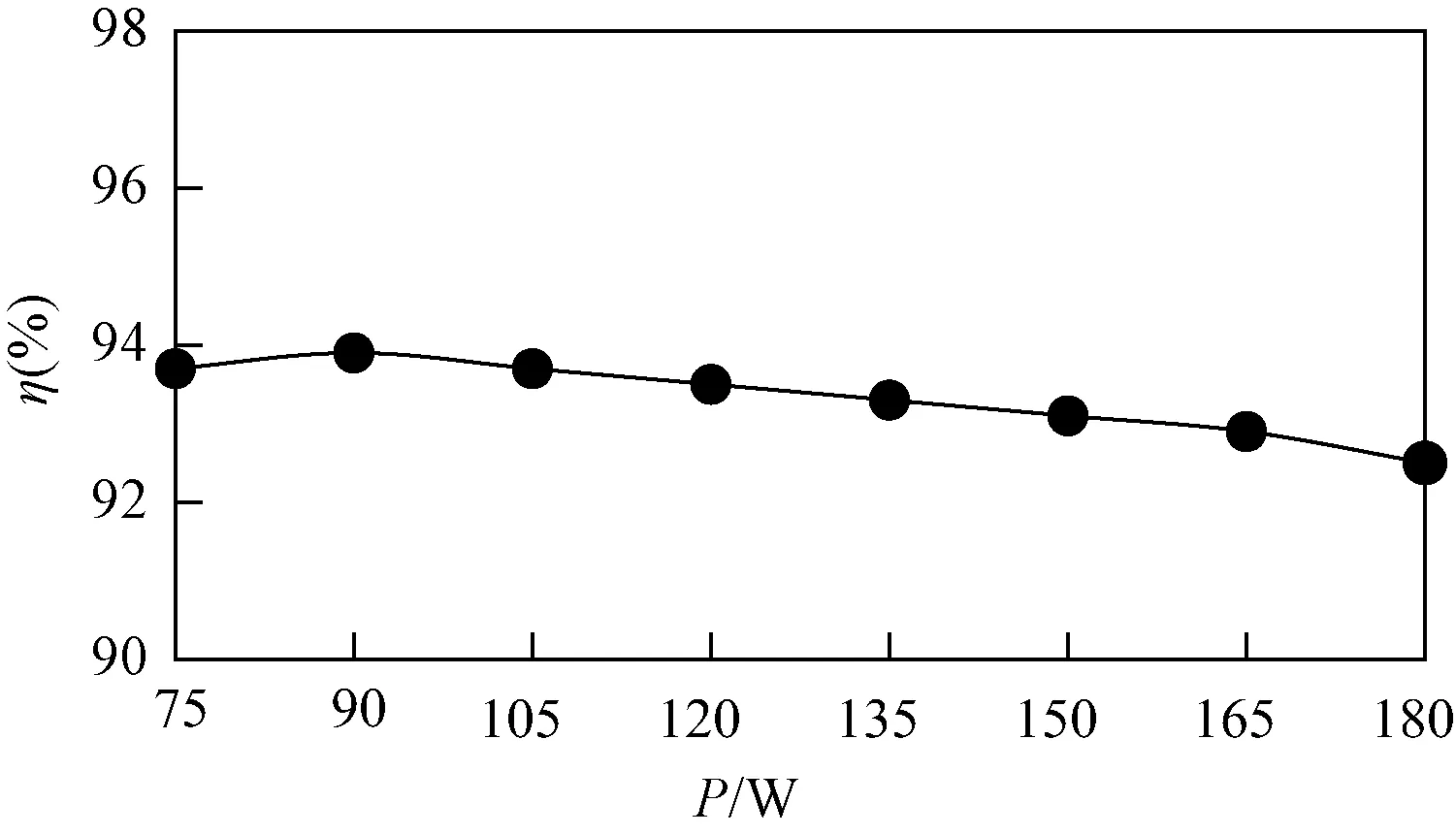
圖20 效率曲線Fig.20 Efficiency curve

5 結論

為進一步提升DC-DC變換器的增益，提出了一種雙耦合電感非隔離高增益變換器拓撲，分析了其CCM-CCM、CCM-DCM和DCM-DCM狀態下的工作原理，與傳統的直流變換器相比，具有如下優點：

(1)在相同占空比下，所提拓撲具有更高的電壓增益，更低的開關管電壓應力，且使用單管控制，降低了控制的復雜度。

(2)輸出電容和輸出二極管同時作為無源吸收回路，充分利用漏感能量，提高變換器的功率密度。

(3)對于雙耦合電感結構，可以通過調節占空比D和耦合電感匝比靈活調節變換器的電壓增益，有效地避免變換器工作在極限占空比的情況。