新型RISE-LADRC逆變器電壓控制策略

劉 勇，沈貴妃，章 兢,2，盤宏斌，馬士翔

(1.湘潭大學自動化與電子信息學院，湖南 湘潭 411105；2.湖南大學電氣與信息工程學院，湖南 長沙 410082)

1 引言

傳統化石能源短缺和環境污染問題成為制約世界經濟發展的兩大阻礙[1]。具有污染少、可靠性高、能源利用效率高等優點的可再生能源和分布式發電成為應對能源、資源短缺的有效途徑[2，3]。目前，微電網技術作為可再生能源和分布式發電的有效利用形式已成為研究的熱點[4]。在微電網中，逆變器是連接分布式電源(Distributed Generation,DG)和各種負載的樞紐，其對系統的穩定起到關鍵作用。當離網逆變器中出現非線性負載和不平衡負載等強擾動時，傳統自抗擾控制(Active Disturbance Rejection Control，ADRC)的抗擾性能還有待提升。因此，研究如何提高微網逆變系統的抗擾能力具有現實意義。

近年來，為了提高微網逆變器的抗擾性能，很多學者都提出了針對含擾動系統的控制方法，如自適應控制[5，6]、魯棒控制[7，8]、滑模控制[9-11]等。自適應控制能通過自適應控制律來設計參數，可較好地處理參數不確定性，但擾動很大時的抗擾能力不足。魯棒控制可以較好地解決未建模動態和擾動的問題，但魯棒控制是高增益控制，可能受到高頻噪聲的影響。滑模控制能有效地抵抗未建模動態、參數攝動引起的干擾和不確定，實現系統在滑模面上的漸進穩定，但是傳統滑模控制包含不連續控制會產生抖振。在處理擾動帶來的不確定性時，這些方法因為特定的局限性不利于工程實用[12]。ADRC是韓京清先生針對比例-積分-微分(Proportion Integral Derivative,PID)控制器中存在的問題而提出的一種非線性控制策略，ADRC可以將系統中未建模動態、不確定動態和外部擾動全部視為總擾動，通過擴張狀態觀測器(Extended State Observer,ESO)對總擾動進行實時估計及補償，從而消除擾動對系統的影響[13-15]。因此，ADRC不依賴于精確的數學模型，具有算法簡單、魯棒性強、動態性能好等優點[16]。而ADRC中非線性結構的理論分析困難，計算復雜度高，控制器需要調節的參數多[17]。將ESO和狀態誤差反饋律(State Error Feedback,SEF)這兩個主要部分進行線性化處理，提出了線性自抗擾(Linear Active Disturbance Rejection Control，LADRC)，通過對觀測器帶寬和控制器帶寬進行調節就能確定控制器的參數，方法簡單，效果較好[18，19]。擴張狀態觀測器(Linear Extended State Observer,LESO)是LADRC的核心部分，其能實時估計系統中的總擾動，總擾動的反饋補償環節也依賴于LESO，因此，LESO的觀測能力直接決定了LADRC系統的控制精度。為了保證足夠高的觀測精度，需要盡可能地增大觀測帶寬[20]。但是，高觀測帶寬可能帶來初始尖峰現象，估計尖峰會導致系統動態性能下降[21]。另外，文獻[12]分析了增大觀測器帶寬可提高跟蹤性能，但是也會放大高頻噪聲，導致系統控制量受噪聲的影響產生大幅度的高頻振顫。因此，在系統中出現強擾動時，不能只靠增大觀測帶寬來提高控制性能。為了增強抗擾能力，有很多學者提出了不同的改進方案。文獻[22]和文獻[23]通過設計時變增益觀測器來保證觀測誤差收斂，并且有效抑制ESO高觀測帶寬帶來的“初始微分峰值”現象，提高了觀測精度。文獻[24]設計改進二階LADRC，在LESO中引入輸出電壓誤差微分項，增加觀測帶寬以提高LESO的擾動觀測能力，并在LESO中引入一階慣性環節，增強高頻噪聲抑制能力，改進的LADRC具有較好的抗擾能力。上述文獻都是從ESO層面來提高系統的抗擾能力，較少有文獻對控制律進行研究。

綜上，本文針對存在強擾動的離網逆變器系統，提出誤差符號魯棒積分(Robust Integral of the Sign of the Error，RISE)控制律和LADRC相結合的電壓控制策略。首先，對離網逆變器建立數學模型，根據逆變器模型建立被控對象為輸出電壓的LADRC模型。然后，分析了當系統中出現強擾動時，有限的觀測帶寬不能準確地估計擾動，LADRC的控制精度會受其影響。其次，為了減小控制器對LESO的依賴，本文通過設計抗擾能力更強的RISE控制律來代替線性誤差反饋律，RISE控制中的反饋增益能有效地抑制擾動對系統的影響[25，26]，提高系統的控制性能，并利用Lyapunov理論證明了所提控制策略的穩定性。最后，仿真和實驗結果表明，相比傳統LADRC控制，本文所提的RISE-LADRC控制對輸出電壓的跟蹤精度更高，增強了逆變器系統的抗擾能力。

2 微網逆變器建模及LADRC控制器設計

2.1 微網逆變器建模

離網逆變器系統的結構如圖1所示，本文中逆變器采用LC型濾波器進行濾波，DG是分布式電源；Lf、Cf、rf分別為濾波電感、濾波電容和濾波電感寄生電阻；uabc是逆變器橋臂側三相輸出電壓；uoabc是逆變器三相輸出電壓；iLabc是濾波電感三相輸出電流；iCabc是濾波電容三相輸出電流；ioabc是逆變器三相輸出電流；uodq是逆變器輸出三相電壓在dq軸的分量；vodq分別是三相參考電壓在dq軸的分量。

圖1 離網逆變器控制框圖Fig.1 Block diagram of off-grid inverter control

根據圖1的離網逆變器結構，建立LC型離網逆變器在dq坐標系下的數學模型。

dq坐標系下逆變器的數學模型為：

(1)

(2)

式中，ud、uq分別為逆變器橋臂側電壓在d、q軸分量；uod、uoq分別為逆變器輸出電壓在d、q軸分量；iLd、iLq分別為濾波電感電流在d、q軸分量；iod、ioq分別為輸出電流在d、q軸分量；ω為電網電壓的角頻率。

2.2 基于LADRC的電壓控制

對式(2)求導后將式(1)代入得二階微分方程：

(3)

根據式(3)中逆變器系統的輸出電壓uod和uoq來設計LADRC控制器，由于d、q軸方程具有對偶關系，下文中只對d軸進行分析，q軸的分析類似[27]。

由式(3)可知，離網逆變器系統的LADRC被控對象模型表示如下:

(4)

式中，uod為被控目標；b0為控制增益，b0=KPWM/LfCf；KPWM為逆變器增益；u為電壓控制信號d軸分量；f為系統總擾動。

(5)

將式(4)中的f作為擴張狀態變量，根據式(4)建立擴張系統的狀態空間表達式：

(6)

式中，x1、x2、x3為系統的狀態變量；y為系統輸出；x1=uod為逆變器輸出電壓；x2為逆變器輸出電壓的微分；x3=f為系統總擾動；h為總擾動f的微分。

建立LESO擴張狀態觀測器：

(7)

可以求出式(7)的特征方程：

λ(s)=s3+β1s2+β2s+β3

(8)

根據文獻[19]，當特征方程為理想狀態時，λ(s)=(s+ωo)3。

β1=3ωo,β2=3ωo2,β3=ωo3

(9)

取前饋控制為：

(10)

將式(10)代入式(6)，可得

(11)

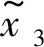
LSEF設計如下：

u0=kp(vod-z1)-kdz2

(12)

式中，kp和kd為控制增益，都是正數。

傳統LADRC控制器由跟蹤微分器(Tracking Differentiator,TD)、LESO、LSEF組成。本文中不使用TD，最終可以得到，傳統LADRC控制器的整體結構如圖2所示。

圖2 傳統LADRC整體控制圖Fig.2 Block diagram of traditional LADRC control

3 設計RISE-LADRC控制器

3.1 設計RISE控制律

(13)

定義RISE控制律的誤差變量為：

(14)

式中，α1和α2是RISE控制的控制增益。

將式(13)代入式(14)中得：

(15)

結合式(13)～式(15)得：

(16)

結合式(14)對式(16)做變換，可得：

(17)

將式(11)、式(15)代入式(17)中：

(18)

對式(18)求導，結合式(14)和式(15)，可得

(19)

(20)

假設擾動Nd存在如下關系：

‖Nd‖≤ξ1

(21)

(22)

式中，‖·‖為2范數。

引理1[28]：定義輔助變量L(t)為

L(t)=r(Nd-βsgn(e2))

(23)

如果符號函數增益β滿足以下條件：

(24)

定義的輔助函數P(t)為：

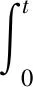
(25)

則有P(t)恒大于0。

輔助函數P(t)的導數為：

(26)

定義李雅普諾夫函數為：

(27)

對式(27)求導，結合式(14)、式(15)和式(26)得出：

(28)

令

(29)

對式(29)進行積分，結合式(14)，則可以得到RISE控制律為：

(30)

式中，α1、α2、ks為控制增益；β為符號函數增益。

3.2 設計RISE-LADRC控制器

本文中的RISE-LADRC控制器由LESO和RISE控制律組成。根據式(7)、式(10)、式(14)和式(30)可以得到RISE-LADRC控制器的結構如圖3所示。

圖3 RISE-LADRC控制結構圖Fig.3 RISE-LADRC control structure diagram

4 穩定性分析

定理1給定一個系統如式(11)所示，若在滿足式(24)的前提下，通過調節控制增益α1、α2和ks使其滿足如下關系：

(31)

則式(30)中提出的RISE控制律能夠保證e1、e2和r有界。

證明：根據穩定性分析，選取李雅普諾夫函數如式(27)所示。

將式(29)代入式(28)可得出：

(32)

文獻[29]中證明被控對象的動態模型未知且擾動有界時，ESO的估計誤差是有界的，即存在：

(33)

?為一個有限正數。

z=[e1e2r]T

(34)

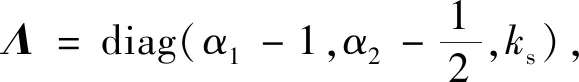
(35)

根據式(31)、式(34)和式(35)，定義如下緊集：

(36)

實現e1、e2和r有界的前提是控制增益α1、α2和ks滿足式(31)，且根據式(36)可知，控制增益α1、α2和ks的取值越大則收斂速度越快，故控制增益α1、α2和ks的值可適當取大一點。

5 仿真及實驗驗證

5.1 仿真驗證

為了驗證本文提出的RISE-LADRC電壓控制策略的可行性和有效性，基于Matlab/Simulink仿真平臺，搭建三相離網逆變器系統仿真模型。表1～表3分別為逆變器仿真參數、二階RISE-LADRC控制器參數、二階傳統LADRC控制器參數。

表1 逆變器仿真參數Tab.1 Inverter simulation parameters

表2 二階RISE-LADRC控制器參數Tab.2 Second-order RISE-LADRC controller parameters

當離網逆變器系統出現不平衡負載和非線性負載工況時，分別采用RISE-LADRC、傳統LADRC兩種不同控制策略對上述工況進行仿真對比分析。

表3 二階傳統LADRC控制器參數Tab.3 Second-order traditional LADRC controller parameters

工況1：不平衡負載

0～0.1 s系統僅接入P=10 kW、Q=200 Var的公共負載，在0.1s時在負載端a相和c相間接入一個電阻Rb模擬不平衡負載。

圖4(a)、圖4(b)分別為兩種不同控制策略下的三相輸出電壓波形圖，0.1 s前負載端只接有公共負載，RISE-LADRC和傳統LADRC中三相電壓波形都比較平滑；0.1 s接入Rb=30 Ω的不平衡負載后，圖4(a)中RISE-LADRC的三相輸出電壓波形發生微小抖動，迅速恢復到較好的平衡狀態；圖4(b)中傳統LADRC的三相輸出電壓波形出現明顯的不平衡現象。圖4(c)和圖4(d)分別為0.1 s時接入20 Ω、30 Ω、40 Ω、50 Ω的不平衡負載情況下的輸出電壓不平衡度對比圖；圖4(c)和圖4(d)分別為兩種不同控制策略下，不同阻值的負載對應的輸出電壓的不平衡度圖，由圖4(c)可知，RISE-LADRC輸出電壓的不平衡度受不平衡負載的影響較小，達到穩態時輸出電壓不平衡度皆低于0.5 %；由圖4(d)可知，傳統LADRC控制時，接入的不平衡負載阻值越小，對輸出電壓不平衡度的影響越大，達到穩態時輸出電壓不平衡度都高于0.5 %，最高達到1.9 %。綜上分析，RISE-LADRC控制能更有效地抑制不平衡負載帶來的電壓不平衡現象。

圖4 接入不平衡負載結果對比Fig.4 Comparison of results with two-phase unbalanced load

不平衡負載Rb=30 Ω的情況下，圖5(a)為兩種不同控制策略下d軸輸出電壓響應時間圖，其中，RISE-LADRC輸出電壓的響應時間為0.002 8 s，而傳統LADRC輸出電壓的響應時間為0.014 s；圖5(b)為兩種不同控制策略下d軸輸出電壓的跟蹤誤差對比圖，RISE-LADRC輸出電壓標幺值的波動范圍為0.996～1.005 pu；傳統LADRC輸出電壓標幺值的波動范圍為0.979～1.022 pu。綜上可知，RISE-LADRC的快速性更好、跟蹤誤差更小、跟蹤精度更高。

圖5 不平衡負載條件下的動態性能圖Fig.5 Dynamic performance graph under non-linear load conditions

工況2：非線性整流負載

0～0.1 s系統僅接入P=10 kW、Q=200 Var的公共負載，在0.1 s時在負載端接入一個整流負載Rf模擬三相非線性負載。

圖6(a)、圖6(b)分別為兩種不同控制策略下三相輸出電壓波形圖，0.1 s前負載端只接有公共負載，RISE-LADRC和傳統LADRC中三相電壓波形都比較平滑，波形畸變較小；0.1 s接入Rf=30 Ω的非線性負載后，兩種控制策略都能使系統保持穩定運行。但是，由圖6(c)和圖6(d)可知，RISE-LADRC的三相輸出電壓總諧波失真(Total Harmonic Distortion，THD)為2.58 %，傳統LADRC的三相輸出電壓THD為4.52 %，傳統LADRC的三相輸出電壓波形發生更加嚴重的畸變。圖6(e)為0.1s時分別接入25 Ω、30 Ω、35 Ω、40 Ω、45 Ω、50 Ω、55 Ω、60 Ω的非線性負載，不同阻值對應RISE-LADRC的三相輸出電壓THD分別為2.96 %、2.58 %、2.28 %、2.08 %、1.88 %、1.73 %、1.59 %、1.51 %，不同阻值對應傳統LADRC的三相輸出電壓THD分別為5.17 %、4.52 %、3.99 %、3.57 %、3.28 %、3.04 %、2.79 %、2.61 %。綜上分析，在接入不同阻值的非線性負載情況下，RISE-LADRC對諧波的抑制能力強于傳統LADRC。

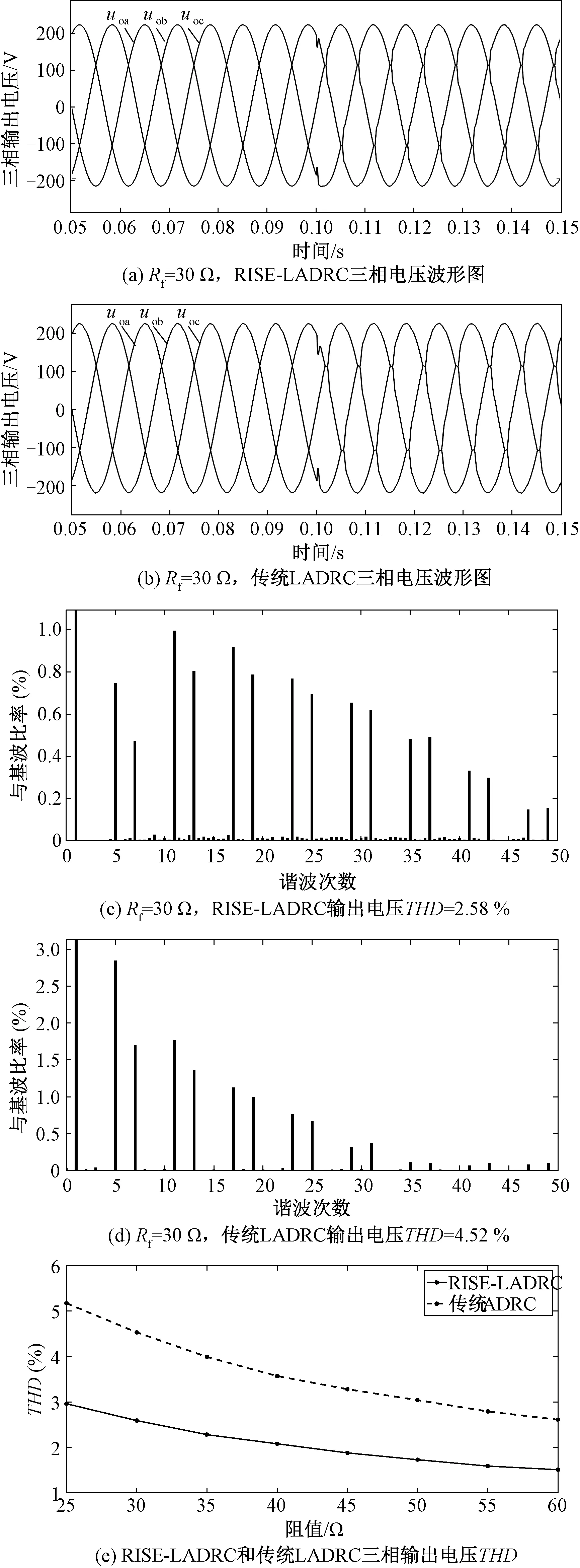
圖6 接入三相非線性負載結果對比Fig.6 Comparison of results with three-phase nonlinear load

非線性負載Rf=30 Ω的情況下，圖7(a)為兩種控制策略下d軸輸出電壓響應時間圖，其中，RISE-LADRC輸出電壓的響應時間為0.003 5 s，而傳統LADRC的響應時間為0.015 s；圖7(b)為兩種不同控制策略下d軸輸出電壓的跟蹤誤差對比圖，RISE-LADRC輸出電壓標幺值的波動范圍為0.991～1.005 pu，傳統LADRC輸出電壓標幺值的波動范圍為0.982～1.015 pu。綜上可知，RISE-LADRC的快速性更好、跟蹤誤差更小、跟蹤精度更高。

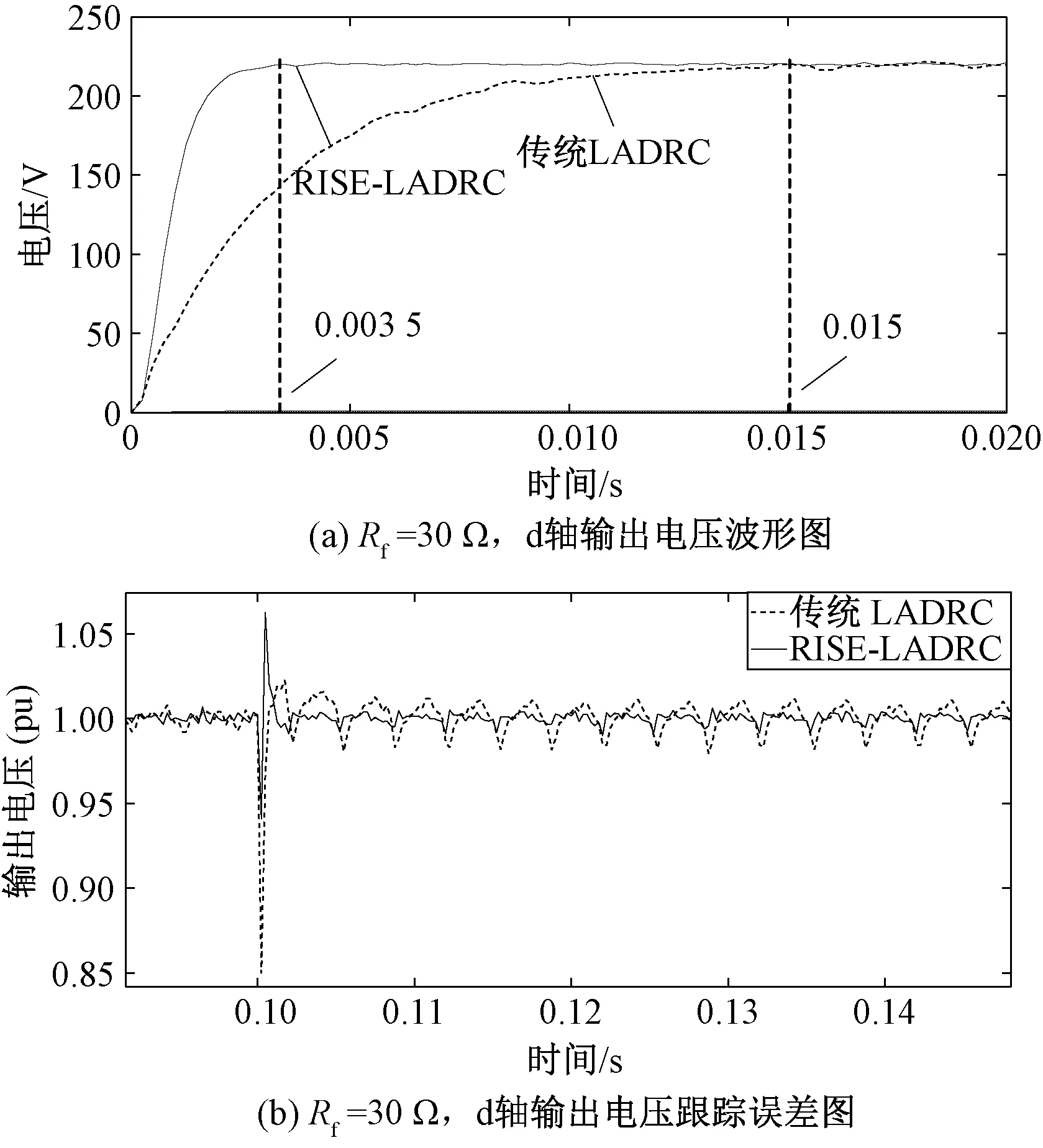
圖7 非線性負載條件下動態性能圖Fig.7 Dynamic performance graph under non-linear load conditions

5.2 實驗驗證

為了進一步驗證所提控制策略的正確性和可行性，使用青銅劍科技公司實驗設備搭建了LC型離網逆變器系統樣機，如圖8所示。逆變器系統采用三相全橋電路，硬件包括控制器、驅動保護電路和采樣電路。實驗控制芯片采用TI公司生產的TMS320F28335芯片，PWM波由TMS320F28335芯片的ePWM模塊生成，主電路和控制器的參數與仿真保持一致。

圖8 實驗樣機Fig.8 Experimental prototype

為了驗證本文提出的RISE-LADRC控制策略對帶不平衡負載擾動的抑制能力，在負載端接入50 %線性平衡負載，再在ac相跨接30 Ω電阻模擬不平衡負載，實驗結果如圖9所示。圖9(a)、圖9(b)分別為不平衡負載工況下的三相輸出電壓、電流波形。可以看出，在不平衡負載條件下，本文提出的RISE-LADRC控制策略能保證逆變器三相輸出電壓保持平衡。

圖9 帶不平衡負載的輸出電壓、電流波形Fig.9 Output voltage and current waveforms with unbalanced load

圖10 帶非線性負載的輸出電壓、電流波形Fig.10 Output voltage and current waveforms with nonlinear load

為了驗證本文所提控制策略對帶非線性負載擾動的抑制能力，在負載端接入三相整流橋，三相整流負載電阻為60 Ω，實驗結果如圖10所示。圖10為三相整流非線性負載工況下的逆變器三相輸出電壓和a相輸出電流波形，受非線性負載的影響，三相輸出電壓均發生畸變，本文提出的RISE-LADRC控制策略的電壓波形THD為2.31 %。

圖11 線性負載由空載到滿載的輸出電壓、電流波形Fig.11 Output voltage and current waveforms of linear load from no load to full load

圖12 線性負載由滿載到空載的輸出電壓、電流波形Fig.12 Output voltage and current waveforms of linear load from full load to no load

圖11和圖12分別為逆變器線性負載從空載變化到滿載、滿載變化到空載時a相輸出電壓和電流波形，由此可知，所提控制策略在負載切換過程中輸出電壓大小基本保持不變，輸出電流始終保持穩定，且無超調現象。

綜上分析可得，在不平衡負載、非線性負載以及負載切換等擾動情況下，本文所提的控制策略表現出較好的抗擾能力。可以說明，所提控制策略能有效地加強擾動抑制能力，使得系統具有較好的抗擾性能，驗證了本文提出的控制策略的可行性。

6 結論

當離網逆變器中出現不平衡負載和非線性負載等強擾動時，傳統LADRC的抗擾能力不足，針對此問題，本文提出一種新型RISE-LADRC控制策略，其中LADRC和RISE都不依賴精確的數學模型。所提RISE-LADRC控制策略通過LESO實時估計系統中的總擾動，結合RISE控制有效地抑制擾動，提高系統的跟蹤性能，并通過李雅普諾夫穩定性定理驗證了系統的穩定性。在LESO觀測帶寬一定的情況下，對RISE-LADRC控制策略和傳統LADRC控制策略進行仿真對比分析。仿真結果表明，系統中存在強擾動時，RISE-LADRC控制策略的輸出電壓畸變率更低，輸出電壓能準確地跟蹤參考輸入，達到穩態時的快速性更好，有效地降低了強擾動對跟蹤性能的影響。因此，本文提出的RISE-LADRC控制策略具有更好的抗擾能力和動態響應性能。