架構課程期待與學生學習之間的橋梁
——浙教版《市場里的數》單元整合實踐與反思

文|陳敏 邊 聰 王俊

為了方便研究，“QUASAR”區分出課程任務發展的不同階段，分別為“期望的課程”“實施的課程”和“實現的課程”。“期望的課程”指教學大綱中規定、教材編寫中預設的課程；“實現的課程”是指最終學生實際的學習收獲。從期望的課程到實現的課程，轉化的關鍵在于實施的課程：即由教師主導的、在課堂中實際發生的教學過程。

數學任務框架

圖1 數學任務在課堂教學中的展開過程示意圖

“單元整合”是當下的一個熱點議題。如果用上述框架來理解單元整合的問題，我們認為：教師所做的單元整合，仍屬于“實施的課程”范疇。即，教師做單元整合的根本目的不是要創編一套新的學習材料（“期望的課程”），而主要是如何利用好現有的學習材料（即教材），比照本班學生的學習實際，做針對性的增補、刪減、重構，以促進學生的學習，更好地實現課程預設的目標。簡單地說，是對教材的“班本化”“師本化”。

我們按以下三個步驟開展單元整合設計：第一，分析教材設定的單元目標及預設的學習路徑；第二，結合經驗和實測，明確本班學生的認知基礎和潛能、偏好；第三，對比前兩點，發現期望課程與學生實際學習能力之間的差異和距離，進行整體的單元整合和個別的環節重構。

圖2 單元整合流程示意圖

下面以浙教版一年級下冊第三單元《市場里的數》為例，作具體闡述。

一、教材分析

1.單元內容分析。

浙教版教材是國家審定的、適合部分較發達地區（學校）使用的實驗教材，在學習內容組織方面獨具特色。

圖3 浙教版一年級下冊第三單元目錄

認真審讀本單元的目錄，可以發現，前三課均圍繞數的意義：第一課時聚焦計數單位的認識；第二課時主要是對百以內數的單位構成進行分析，從基數角度理解數的意義；第三課時通過尋找“百數表”規律的活動，引導學生感知數序，從序數角度進一步體會十進計數結構、數與數之間的關系，完善數的概念。后三課則可以理解為數的概念在不同問題情境中的應用，具體包括：數的大小比較（單位大小比較或同單位個數比較）、不進位加（單位累計或繼續數數）、不退位減（單位消減或倒數）。從而，可概括出教材預設的本單元目標是圍繞“單位”的概念，在靈活多變的情境中，建構和理解數的意義。教材預設路線是：先“明理”后“應用”，是一種演繹的路徑。

2.知識點序列分析。

好的教材往往具有知識內容螺旋上升的編排特點。我們進一步尋找與本單元直接相關的基礎內容和發展章節。結果發現：在整數的認識這個序列上，本單元之前，教材已安排有“10 與幾”（一年級上冊）、“40以內數的認識”（一年級下冊）。即，從教材邏輯講，本課之前，學生已經具有兩位數單位意義的分析經驗（只不過數的大小在40 以內而已）。

而本單元之后，學生還將繼續認識“三位數、四位數的讀寫”（二年級下冊），“十進制計數法”和“萬以上數的讀寫”（四年級下冊）。關鍵仍在計數“單位”的概念。任何一個數的意義都可分析為兩層：（1）以什么單位計數？（2）有幾個這樣的計數單位？（有時可能只用一個單位計數，有時會用幾個單位復合計數）這樣的理解還可以進一步推廣到小數、分數。

二、學生調研

1.設計前測試卷。

學生對數的認識情況如何？為探明教學的實際基礎，我們設計了單元前測卷，以“單位”的思想為核心，主要測試兩方面：（1）數的意義的基礎認識；（2）應用數的意義解決問題。

前測卷“數的意義”部分，安排了多元表征的問題。

前測卷“數的應用”部分，設計了兩位數與一位數以及兩位數與兩位數的加減法（加法不進位、減法不退位），包括直接計算問題和應用問題，應用問題又涉及加減法的各種情境意義，如合并、增加、減少、相差等。

2.學生實測結果。

杭州市勝利小學一年級共125 名學生參加了前測。實施時，學生在自然狀態下，以課堂作業的形式完成前測。時間在30 分鐘以內。期間，教師不做任何提示和點評。

結果發現：

（1）關于數的意義。

①對計數單位的認識掌握得不錯。

如圖4，前測卷第1 題、第5 題和第7 題，正確率分別達97.6%，96.8%和90.4%，從中可以發現學生對于計數單位的認識掌握得不錯，能夠通過語言、圖像等準確表征23 的含義。說明浙教版教材前期對計數單位的強調，以及分段學習兩位數的安排是有效的。

圖4 兩位數的多元表征考查題

②對數的抽象表征仍有困惑。

如圖4，前測卷第4 題、第7 題和第8 題的正確率分別為80.8%，90.4%和88.8%，部分學生對數軸和算式這樣數學化的表征仍存在困難和誤會。

③自主表征的能力弱，數概念的結構化程度不高。

在“用圖畫出23”這道題目中，學生的作品可分類為——

計數器或數位表人數百分比（%）34.412.832.011.2表征方法散點圖 以2，3，5 為計數單位的圖像以10 為計數單位的圖像請你用畫圖的方式表示23。請你用畫圖的方式表示23。請你用畫圖的方式表示23。請你用畫圖的方式表示23。樣例images/BZ_14_1551_2250_1608_2444.pngimages/BZ_14_1718_2260_1866_2403.pngimages/BZ_14_1957_2257_2079_2412.pngimages/BZ_14_2137_2252_2272_2372.png

說明學生雖能看懂他人（教材、問卷）所提供的具有單位結構的各種數的表征，卻沒有內化為其自身的、自覺的對數的認識和把握，亦即學生自身的數概念還沒有結構化。

（2）關于應用數概念解決加減法問題。

①對加法運算意義的掌握優于減法運算意義。

如圖5，第10 題和第11 題是加法情境問題，正確率都是95.2%；第12 題和第13 題是減法情境問題，正確率下降為83.2%和90.4%。可以發現，學生對加法意義的認知優于減法，特別是減法中“相差比較”的問題，出現錯誤的情況最多。

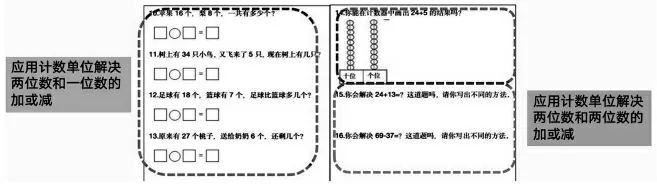
圖5 兩位數加減計算考查題

②加法計算的正確率亦優于減法計算。

對第15 題兩位數加兩位數不進位的加法題，學生用到的計算策略有：a.先湊十，再繼續加，如24+6+7，占33.6%；b.根據數的意義，相同計數單位直接相加，如：20+10=30，4+3=7，24+13=37，占36.8%；c.標準豎式計算，15.2%。對第16 題兩位數減兩位數不退位的減法題，學生用到的計算策略有：a.先減整十數部分再繼續減，如69-30－7，占16%；b.根據數的意義，相同計數單位直接相減，如：60-30=30，9-7=2，69-37=32，占30.4%；c.標準豎式計算，15.2%。

學前加法的正確率為84%，減法的正確率為61.6%。在未學的情況下，初步能夠利用數的意義自主尋求加減計算方法，但算理不自覺，算法不穩定。加法計算的正確率優于減法。

（3）關于數的規律問題。

在前測卷的最后，我們還安排了兩個發現數規律的任務，如下圖6。第17～20 題是數列規律的概括和推理，第21、22 題是數表規律的概括和推理。

圖6 數列和數表規律推理

各題的正確率如下表——

題號171819202122正確率（%）99.270.472.882.475.246.4

可以看到，找規律問題的正確率整體低于前面的常規問題，特別的，學生雖然能夠填出正確的數，但在表達規律時，能同時答到按不同方向“橫看、豎看”和按不同維度觀察“數位、數值”變化的人非常少。可知學生限于表面數字形式的感知，還沒有能夠深入到數的關系、計數的結構等層面深刻理解規律。

三、單元整合與重構

綜上，我們考慮在實際教學中，對目前的教材編排做到一個“堅持”和一個“變化”。

1.堅持：突出“單位”的思想。

（1）堅持計數單位單獨設課教學。

（2）充分展開計數單位計數的過程分析。

將整十數理解為以“10”為單位計數，而一般的兩位數（幾十幾）是綜合“10”和“1”為單位計數。注意對這樣的認識過程及結果展開多元化的表征，發揮學生在表征過程中的自主性，并借助表征之間的比較、溝通和轉換，幫助學生理解數學化的表征的意義，進而形成對數的結構化的認識。

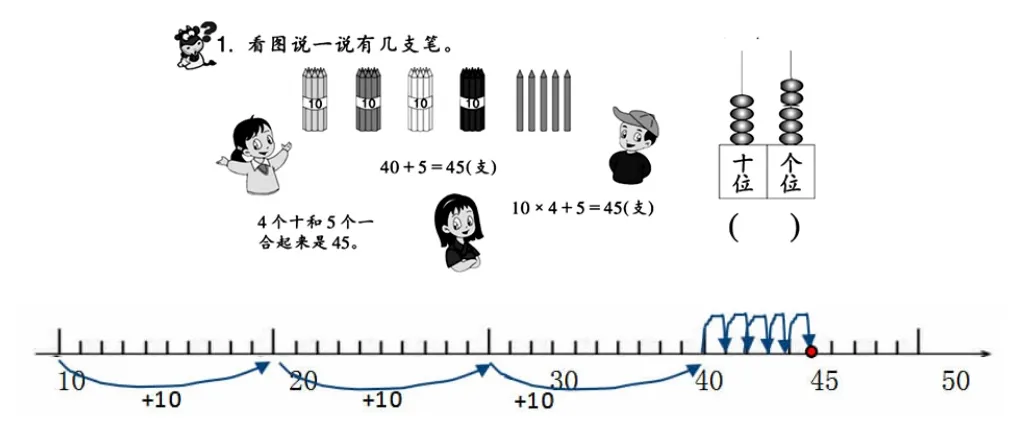
圖7 關于45 的各種結構化表征

（3）引導學生基于數的構成和運算意義，理解加減運算的基本算理。

利用學生目前“朦朧”的算法創造，引導學生基于數的單位去反思和分析各種算法的合理性、關聯性，理解運算意義，對接計數規則，揭示運算原理，從而使學生的計算方法具有自覺性和靈活性，為今后進一步兩位數進位加法、退位減法、多位數加減，甚至分數、小數加減等提供堅實的算理基礎。

2.變化：增加學習的層次。

教材勾畫的是最為理想的且條理清晰、層層遞進的學習過程，而實際上學生需要在個人良莠混雜的認知內容中去偽存真、去粗取精，需要更多的學習時間，更豐富的學習活動去體會材料意圖，反思活動經驗，達到預定的目標。所以擬增加“我認識的100”“生活中的兩位數加減問題”共兩節活動課，貫通校內外的學習，賦予兩位數認識以兒童的視角和個人的意義；另外對百數表“找規律填數”一課進行重構，突出規律表象與計數及計數規則之間的聯系，引導學生感悟規律背后的數學本質。