工字形薄壁梁翼緣彎曲切應力的進一步分析1)

馬志敏 黃昆濤 黃志強 胡畢華

(武漢工程大學機電工程學院，武漢430073)

工字形薄壁梁腹板和外伸翼緣上與翼緣平行的彎曲切應力，現有的材料力學教材[1-6]中已有較為經典和通用的計算公式，但翼緣和腹板交接區域與剪力垂直的切應力和翼緣上與剪力平行的切應力公式，各文獻中給出的結論，值得進一步探討。文獻[2]和文獻[3]中，考慮到腹板很薄，翼緣和腹板交接區域與剪力垂直的切應力近似地沿用了翼緣外伸部分的切應力計算公式。根據這一公式，翼緣對稱軸上與剪力垂直的切應力最大。這一結論顯然與對稱性分析的結果相矛盾。文獻[4]中給出了翼緣上與剪力相平行的切應力計算公式，它沿用了矩形截面梁上的彎曲切應力公式，關于這一公式的正確使用，文獻[5]和文獻[7]中均作了詳細的討論。根據討論的結果，由于翼緣較寬，翼緣上與剪力相平行的切應力沿寬度方向并非均勻分布，直接套用矩形截面梁上的彎曲切應力公式，是不妥當的。本文在現有工字形薄壁梁腹板和外伸翼緣上經典彎曲切應力計算公式的基礎上，利用梁相鄰兩橫截面間的平衡條件，對工字形薄壁梁翼緣上的切應力作進一步分析。

1 理論分析

1.1 工字形薄壁梁上腹板和外伸翼緣上經典彎曲切應力公式的應用

工字形薄壁梁的腹板和外伸翼緣均可視為狹長矩形，根據文獻[3]給出的腹板和外伸翼緣上的彎曲切應力公式，對圖1(a)所示的懸臂梁，1-1截面腹板上的任一位置k-k處(距中性軸距離為y，圖1(b)所示)的切應力可表示為

圖1 工字形截面梁腹板和外伸翼緣上的切應力分析

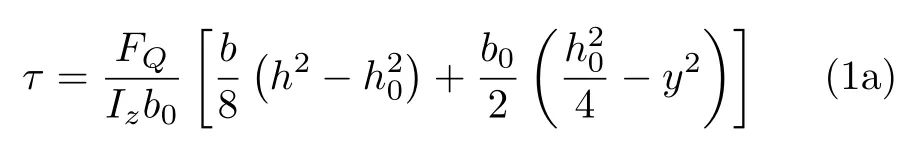
式中，FQ為橫截面上的剪力，Iz為橫截面對中性軸的慣性矩，b0為腹板厚度，h0為腹板高度，h為整個橫截面高度，b為整個橫截面寬度。

在中性軸y=0處有最大切應力，其值為

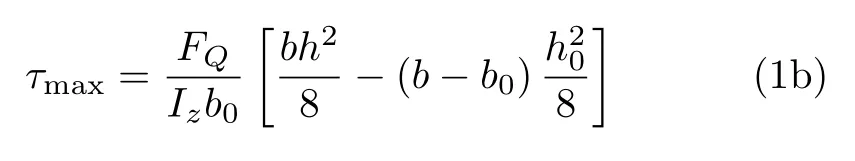
在y=±h0/2腹板上切應力最小，為

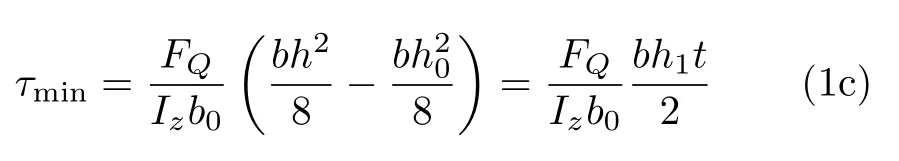
式中，h1為上下翼緣中線間的距離，t為翼緣的厚度。

類似地，截面1-1外伸翼緣任一位置a-a處(距翼緣端點的距離為η)與剪力垂直的切應力可表示為

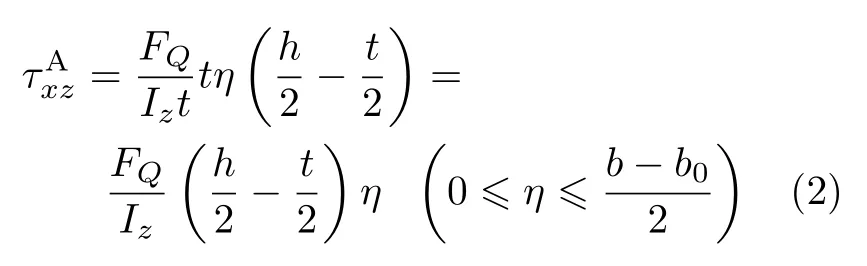
切應力的方向如圖1(c)所示。由式(2)可知，下翼緣右側(外伸部分)橫截面上的切應力大小與到右端點距離成正比。

1.2 翼緣上腹板和翼緣交接區域垂直于剪力方向的切應力

圖2(a)所示為從圖1(a)的懸臂梁中由1-1和2-2截面截出的dx微段，本文中翼緣與腹板交接區域是指該微段上標注為M的陰影部分(下翼緣處未標出)。為求翼緣上腹板和翼緣交接區域垂直于剪力方向(即沿翼緣方向)的切應力，從圖2(a)中取陰影部分B進行分析，受力如圖2(b)所示。

圖2 翼緣和腹板交接區域垂直于剪力方向的切應力分析(續)

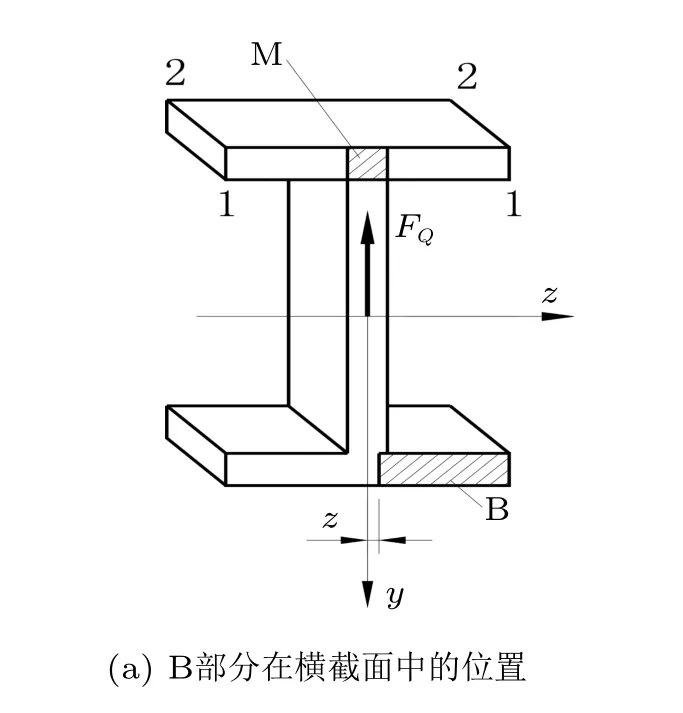
圖2 翼緣和腹板交接區域垂直于剪力方向的切應力分析

由切應力互等定理可知切應力τByx與腹板上最小切應力相等，由式(1c)可知

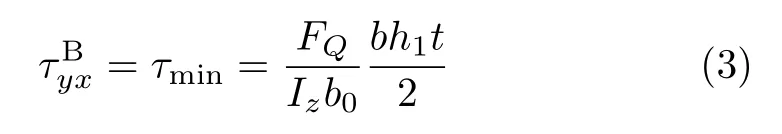
參與B部分x方向上力平衡的，有y和z兩個方向面上的切應力，以及1-1截面和2-2截面上的正應力，由于翼緣很薄，可假設翼緣上垂直于剪力(即平行于翼緣)的切應力τBxz依然沿厚度t方向均勻分布，則有

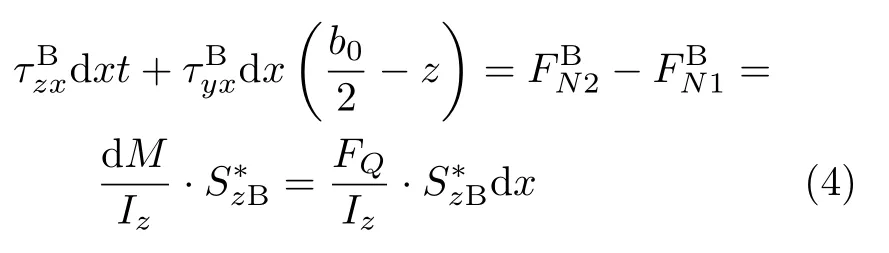
將

和式(3)代入式(4)求解，可得

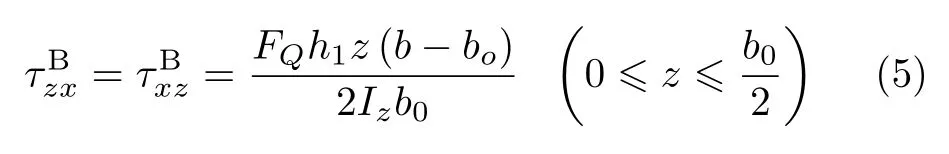
下翼緣左側部分和上翼緣的切應力，同樣可采用上述方法進行分析，只是在分析上翼緣切應力時，要注意截面1-1和2-2的翼緣處，正應力合力為壓力。

1.3 翼緣上平行于剪力的切應力

對于工程中常見的工字形截面，統計數據表明腹板所承擔的剪力，占到整個橫截面上剪力的95%～97%[6]，另外3%～5%的剪力由翼緣承受。由力系的合成關系可知，翼緣上必定存在與剪力方向相同的切應力[4,6]。為得出該切應力的計算公式，依然從圖1(a)所示懸臂梁中截取dx微段進行分析，為方便表達所要分析的區域，重新繪制如圖3(a)所示。由于圖3(a)所示微段上陰影部分C和翼緣外伸部分E和D處的應力邊界條件不一樣，故下面分兩種情況進行考慮。

圖3 翼緣與腹板交接區域平行于剪力的切應力分析

對陰影部分C，其受力如圖3(b)所示。利用切應力互等定理，畫出各面上沿x方向上的切應力，由于腹板很薄，假設在連接處，翼緣上與剪力相同的切應力也是均勻分布的，則由x方向面上的受力平衡條件，可得

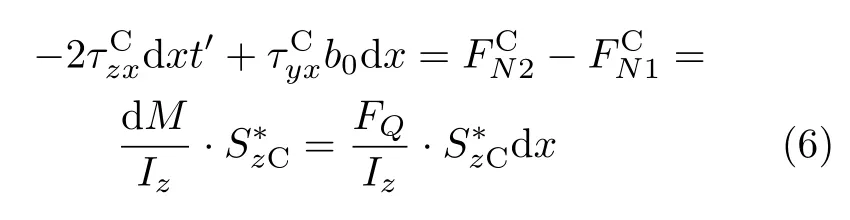
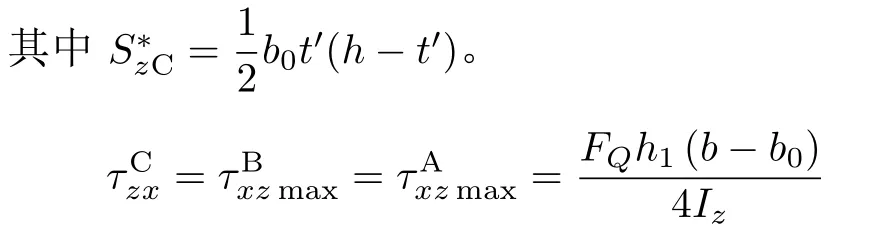
由式(6)可得

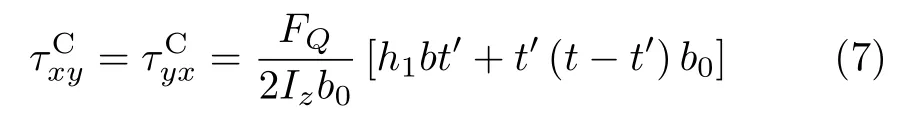
由于b0和t-t′都是關于厚度的一階量，其乘積為厚度的高階量，遠小于h1b，故式(7)中第二項可略去，即有

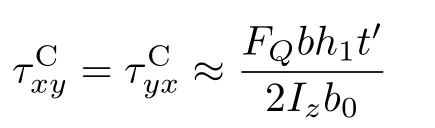
可見，腹板和翼緣交接區域，不同高度處與剪力平行的切應力是不同的，靠近腹板處切應力大，越靠近自由邊，切應力值越小。

對翼緣上的外伸部分(圖3(a)中的D和E部分)，取D部分進行分析(圖3(c))，有

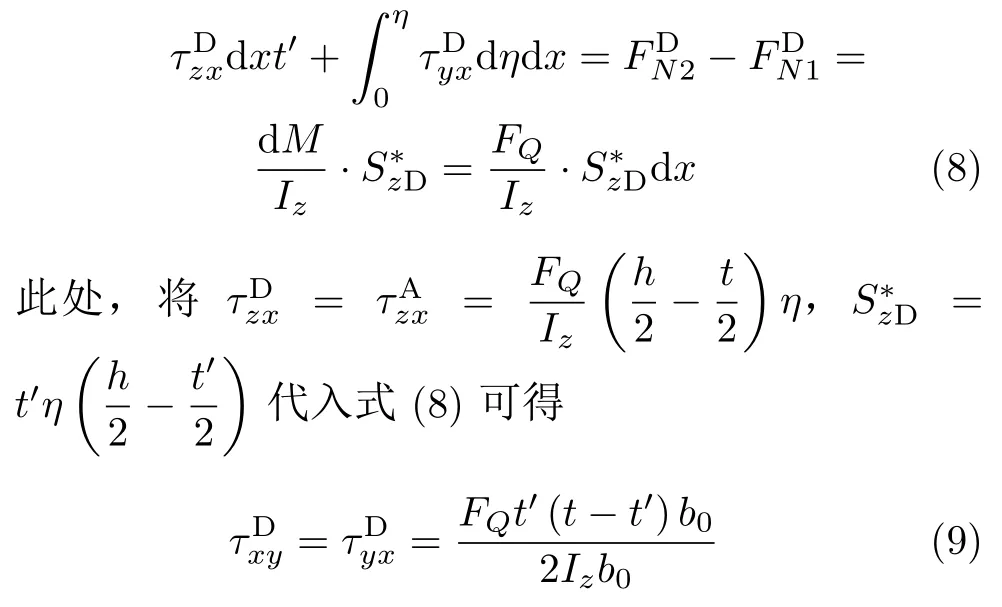
在翼緣同一高度處，沿翼緣寬度b方向的平均切應力為

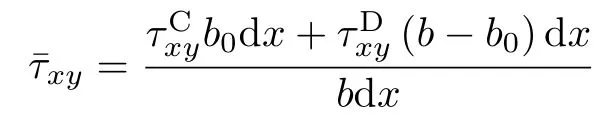
將式(7)和式(9)代入可得

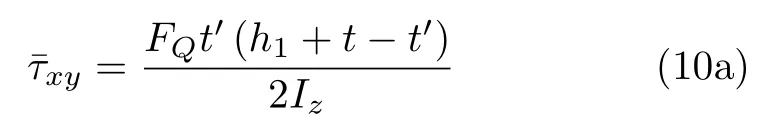
即翼緣上的同一高度處，沿寬度方向的平均切應力沿高度方向亦呈拋物線分布。

在t′=t的位置，有

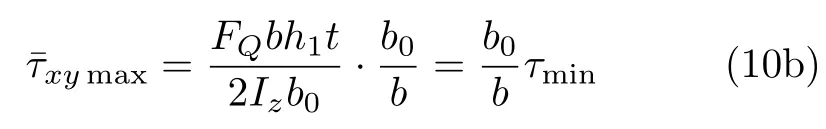
將式(10a)與文獻[4]中第127頁所給出的翼緣上平行于剪力的切應力公式比較，兩者完全相同。因此，文獻[4]中所給出的公式，應視為翼緣上的平均切應力，而不能作為任一點切應力的計算公式。

2 邊界應力的計算分析

2.1 翼緣上與剪力垂直的切應力

腹板和翼緣交接區域，翼緣上與剪力垂直的切應力的表達式為式(5)。將z=0代入，可得

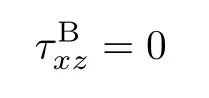
由結構的對稱性亦可知，外力正對稱時，在對稱軸y處，切應力為零，說明式(5)滿足橫截面上的對稱性條件。

在右邊界上，即z=b0/2處，有

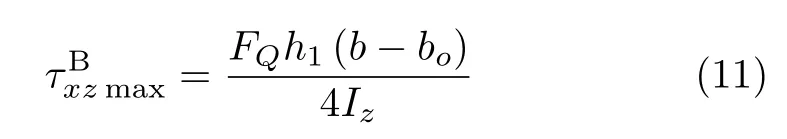
按文獻[3]中結論，在式(2)中，令η=(b?b0)/2，有

說明在外伸翼緣根部，這一切應力是單值連續的。

2.2 翼緣上與剪力平行的切應力

2.2.1 翼緣與腹板交接區域

在式(7)中，令t′=t，有

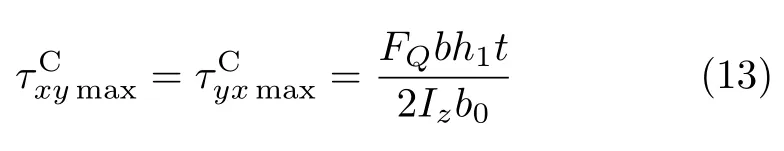
將式(13)和式(1c)進行比較，可知τCyxmax=τmin，說明腹板上的切應力在與翼緣交接邊界處，是連續過渡的。

將t′=0代入式(7)，有

這一結果與外表面無應力的情況相吻合。

2.2.2 外伸翼緣處

在式(9)中，令t′=0和t′=t時，則切應力=0，這與自由表面切應力為零的情況相符。

2.3 翼緣上與剪力垂直切應力和與剪力平行切應力最大值的比較

由上述分析可知，在翼緣與腹板交接處J*點上，如圖4所示，有與剪力平行切應力和與剪力垂直切應力的最大值，由式(11)和式(13)，可得

圖4 工字形梁橫截面翼緣和腹板上的切應力分布圖

工程上常見的工字型鋼截面，b?b0，t≈(1～1.5)b0，故有這兩類切應力的數量級相同，因此，在分析翼緣與腹板交點J*點的應力狀態時，建議同時考慮上述兩種切應力。

3 工字形薄壁梁橫截面切應力分布圖的重新繪制

根據式(2)，式(5)，式(11)和式(12)，可繪制工字形薄壁梁橫截面上，與剪力方向垂直的切應力分布；根據式(1a)，式(10a)和式(10b)，可繪制工字形薄壁梁橫截面上，不同高度處，與剪力方向相同的切應力分布，如圖4所示。由圖可見，與剪力方向垂直的切應力的最大值出現在外伸翼緣根部，在對稱軸y上，這類切應力為零；腹板中部有與剪力方向相同的切應力最大值。需要說明的是，由于翼緣上，與剪力方向相同的切應力在翼緣外伸部分和交接區域的表達式不一樣，故沿高度y方向，其分布圖是由平均切應力公式(10a)繪出。

4 結語

本文在現有工字形薄壁梁經典彎曲切應力理論的基礎上，利用梁相鄰兩橫截面間的平衡條件，深入分析了工字形截面翼緣上平行于剪力的切應力和翼緣與腹板交接區域垂直于剪力的切應力，得出了滿足工字形截面對稱性條件和應力邊界條件的切應力計算公式，繪制了工字形薄壁梁新的切應力分布圖。同時，通過比較，給出了文獻[4]中關于翼緣上平行于剪力的切應力計算公式的準確含義。

需要指出的是，本文所給出的公式是未考慮應力集中的理想化結果，其分析過程沿襲了工字形截面上腹板彎曲切應力的經典分析方法，有助于學生深入理解橫力彎曲中切應力產生的原因，熟悉切應力互等定理，理清彎曲切應力與梁相鄰橫截面中彎曲正應力的平衡關系，確定橫截面上可能危險點的應力情況，于強度分析有一定指導意義，可作為工字形薄壁梁上彎曲切應力分析學習的重要補充。

但須注意的是，工程實際中，腹板和翼緣交接區域一定存在應力集中且應力分布不再均勻[7]，交接處應力會有較大的增大，實際應用中要加以考慮，相關的理論研究值得進一步探討。