計及油缸作用的起重機伸縮臂參數振動分析

劉士明，趙越贏，孟麗霞

（沈陽建筑大學機械工程學院，遼寧 沈陽 110168）

1 引言

伸縮臂是輪式起重機最重要的承載部件，當吊臂起升、下降或突然卸載的過程中，伸縮臂結構可能發生參數共振現象。在我國《起重機設計規范》GB∕T3811-2008中，將起重機伸縮臂靜力穩定性分析模型等效為變截面階梯柱，經研究證明是符合工程實際的[1-2]。因此，在計及油缸作用的起重機伸縮臂參數振動分析中，根據受力特點起升平面內伸縮臂簡化為根部彈性支撐、上端自由的變截面階梯柱模型，起升平面外伸縮臂簡化為根部固支的變截面階梯柱模型。文獻[3]提出了解決周期載荷作用下的動力穩定性問題，以結構動力不穩定區的形式進行表達。文獻[4]通過梁柱的動力微分方程，研究了直桿在周期載荷作用下的動力穩定性。文獻[5]研究了周期載荷下復合材料懸臂梁的動力不穩定性，推導其動力學方程，并對不同參數組合成的組合梁進行參數振動分析。文獻[6]應用Hamilton原理研究了雙柱懸索拉線塔塔柱參數共振，根據Bolotin提供的方法建立臨界頻率方程，從而得到塔柱的主要動力不穩定區。然而，上述方法只適用于一些簡單且截面連續變化的結構，不適用復雜桿系結構。因此一些學者嘗試應用有限單元法求解結構的動力穩定性問題。文獻[7]釆用有限元方法研究空間桿系結構的動力失穩區域，通過Ansys和Matlab軟件進行編程模擬，并將分析結果與Bolotin方法進行對比。文獻[8]采用有限單元法建立了空間網殼結構動力失穩的主動控制方程，通過研究發現可以通過主動控制避開或減小結構動力失穩區域。文獻[9-10]采用有限單元法研究了起重機在周期載荷作用下起升平面外的伸縮臂的動力穩定性，對起升平面內沒有研究，且忽略了變幅油缸的影響。

因此，將考慮變幅油缸的影響，運用Hamilton原理結合有限單元法，建立以Mathieu方程形式表達的伸縮臂參數振動方程，研究起重機伸縮臂動力不穩定區域，為起重機伸縮臂的設計計算提供依據，以指導工程實際應用。

2 伸縮臂參數振動的等效模型

在以往的伸縮臂穩定性分析中，為了方便計算，都忽略了變幅液壓缸的影響，得到的結果很難符合實際工程中的需求。為充分考慮變幅油缸的影響，建立計及變幅油缸的伸縮臂平面內的受力模型，如圖1所示。在起升平面內液壓油缸提供轉動的自由度，假設油缸的剛度為無窮大，則伸縮臂油缸以下的基本臂即l0段連同變幅油缸可以等效為一個轉動剛度為K1的彈性支撐。

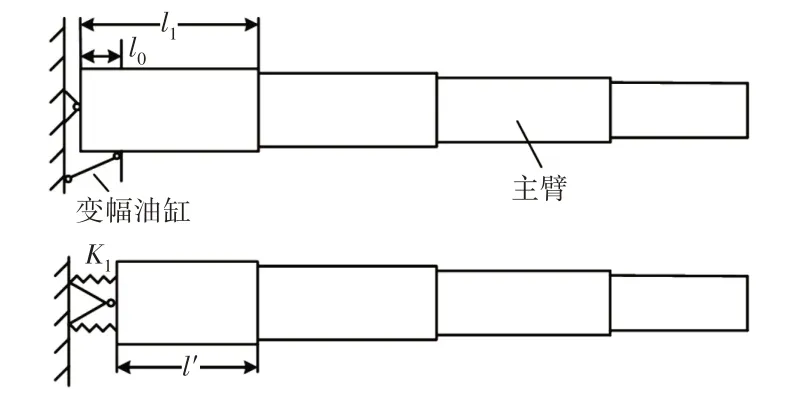
圖1 油缸轉動剛度計算模型Fig.1 Cylinder Rotational Stiffness Calculation Model

文獻[11]給出了K1的計算方法，長度為l0的兩端鉸接柱在頂端受力矩M時其柱段轉角為：

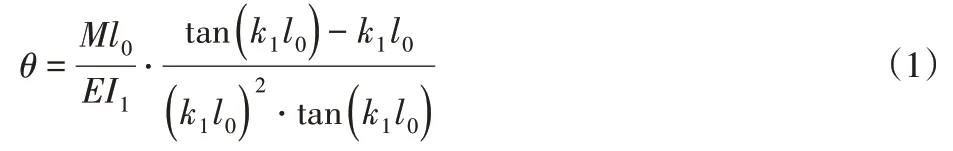
當令M=1時，得到柱端柔度，其倒數就是所求的液壓油缸的轉動剛度：

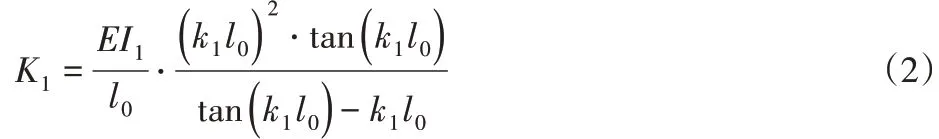
因此，起重機伸縮臂在軸向周期載荷P（t）作用下起升平面內動力穩定性分析等效模型，如圖2所示。即為根部彈性支撐的多級階梯柱模型。

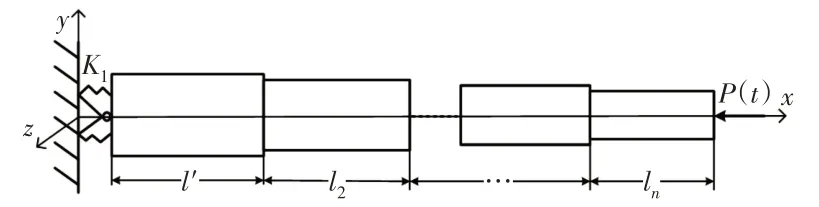
圖2 平面內伸縮臂的動力穩定分析模型Fig.2 Dynamic Stability Analysis Model of Telescopic Arm in Plane

在起升平面外變幅油缸不能承受載荷，因此，根據受力特點將起重機伸縮臂在軸向周期載荷P（t）作用下起升平面外動力穩定性分析模型等效為伸縮臂根部固定的懸臂階梯柱模型，如圖3所示。

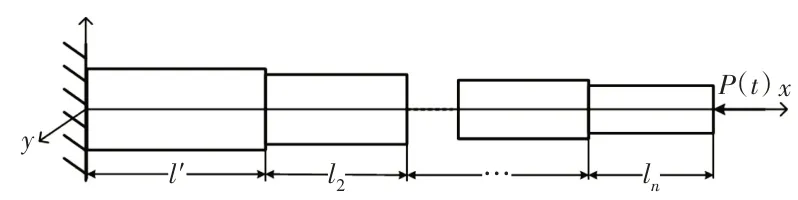
圖3 平面外伸縮臂的動力穩定分析模型Fig.3 Dynamic Stability Analysis Model of Out-of-Plane Telescopic Arm

3 參數振動方程和臨界頻率方程

由參考文獻[9]可知，忽略軸力P（t）引起的軸向位移，根據能量原理，單元的動能T e、彎曲應變能、外力做功的值為：

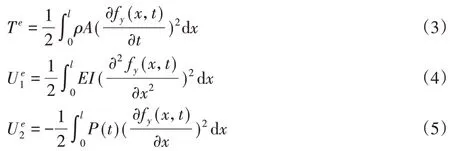
式中：f y(x，t)—單元的橫向位移；l—單元長度；E—彈性模量；A—截面面積；I—慣性矩；ρ—密度。

令梁單元的質量矩陣為M e，線性剛度矩陣為K e0，單位幾何剛度矩陣為S e，根據非線性有限元理論得到：

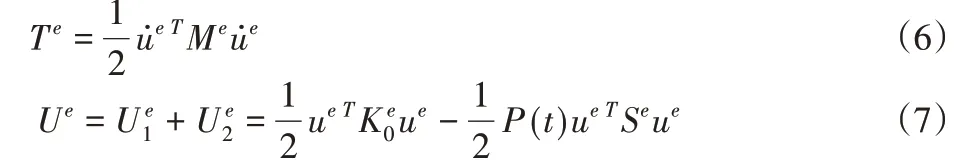
設周期載荷P(t)=P0+P tcosθt，將式（6）和式（7）代入拉格朗日方程，得到無阻尼時系統的參數振動方程：

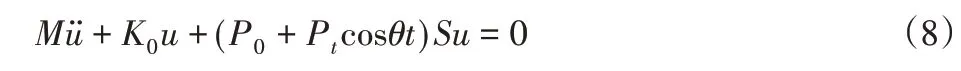
在組裝系統的整體剛度矩陣時，考慮到液壓油缸提供轉動剛度的影響，應將油缸的等效彈簧剛度K1加到剛度矩陣K0中：

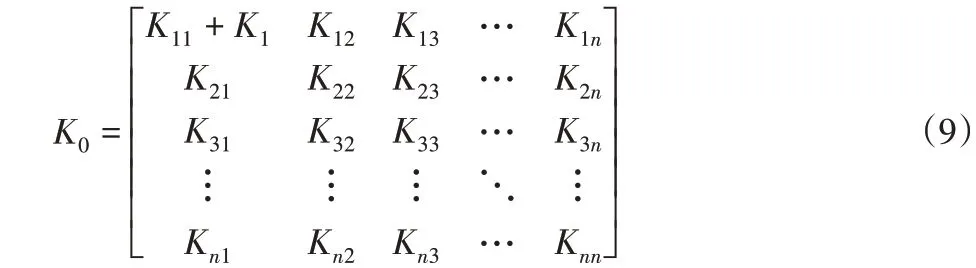
考慮阻尼時，整個系統的參數振動方程變為：

在工程上常將其它形式的阻尼按照它們在一個周期內能量耗損相等的原則，折算成等效粘性阻尼，則此時系統的阻尼矩陣的表達式為：

式中：α—頻率無關的常數。

將式（11）代入式（10）得到考慮阻尼時伸縮臂的參數振動方程為：

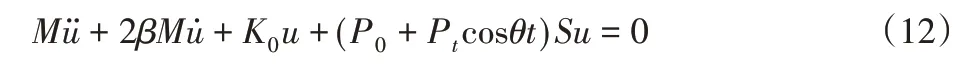
式中：β—無量綱阻尼系數

式（10）和式（12）是Mathieu方程，由方程性質可知，方程的解具有周期性，周期分別為2T和T。令其解的表達式分別為：

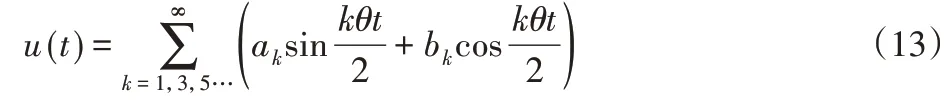
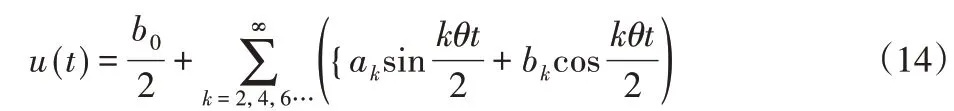
將式（13）和（14）分別代入式（12）中。令sin(kθt∕2)和cos(kθt∕2)的同類項系數等于零，得到兩個齊次線性方程組，令矩陣的系數行列式為零，則可得到有阻尼時的臨界頻率方程：

工程實際中最危險的是k=1（第一動力不穩定區域）和k=2（第二動力不穩定區域），所以令k=1、2，則有阻尼時第一和第二動力不穩定區域的臨界頻率方程分別為：

令β=0，可得無阻尼時的第一和第二動力不穩定區域的臨界頻率方程：

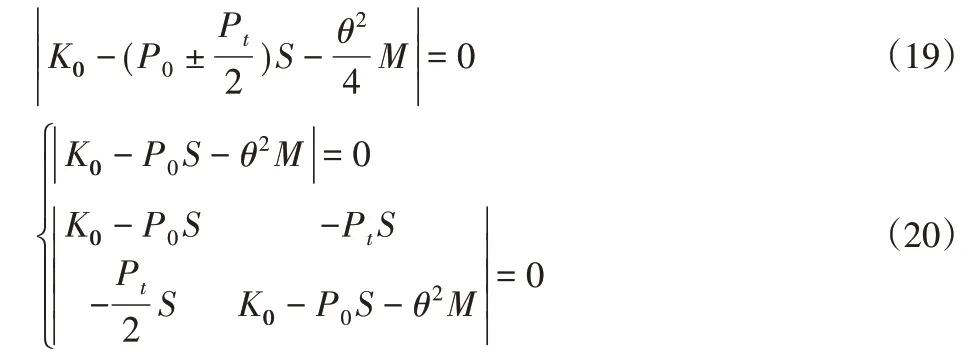
4 算例分析

以工程中常見的五節起重機伸縮臂為例，研究伸縮臂在周期載荷P(t)=P0+P tcosθt作用下伸縮臂的動力穩定性即參數振動，其平面內和平面外動力穩定性計算模型，如圖4、圖5所示。

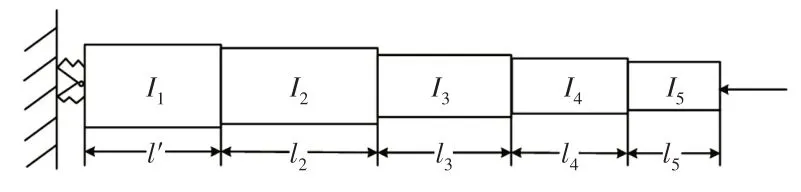
圖4 平面內五節臂計算簡化模型Fig.4 Simplified Model for Plane Five-Section Arm Calculation

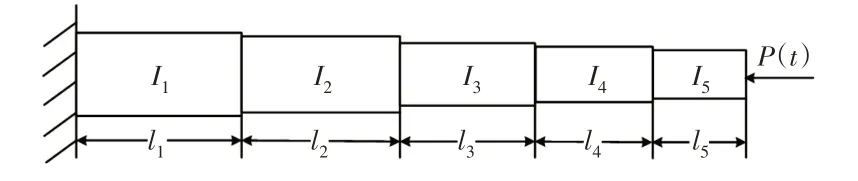
圖5 平面外五節臂計算簡化模型Fig.5 Simplified Model for Out-of-Plane Five-Section Arm Calculation

變截面階梯梁的總長度為L=30m，各段長度分別為l1=0.24L，l2=0.19L，l3=0.19L，l4=0.19L，l5=0.19L。彈性模量E=200GPa，截面慣性矩I1=1.1786×10-2m4，I2=I1∕1.3，I3=I2∕1.3，I4=I3∕1.3，I5=I4∕1.3，密度ρ=7800kg∕m3，變幅油缸上鉸點以下基本臂的長度l0=3m，圖中l′=l1-l0。為了便于分析動力不穩定區域，設P0=0，主要研究其第一、二動力不穩定區。橫坐標定為載荷幅值P t，縱坐標定為臨界振動頻率θ*，做出伸縮臂在平面內和平面外的動力穩定性分析曲線，如圖6、圖7所示。將平面內外的第一動力不穩定區疊加比較，如圖8所示。

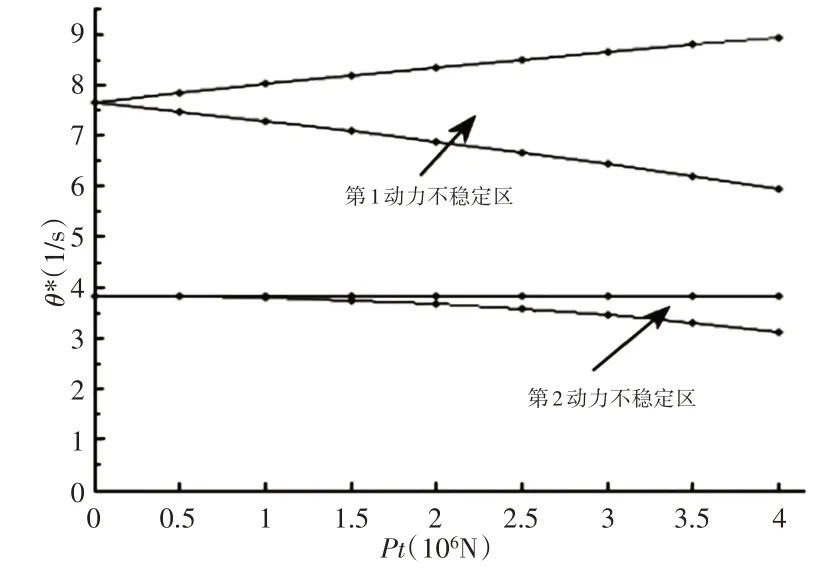
圖6 平面內動力穩定性曲線Fig.6 In-Plane Dynamic Stability Curve

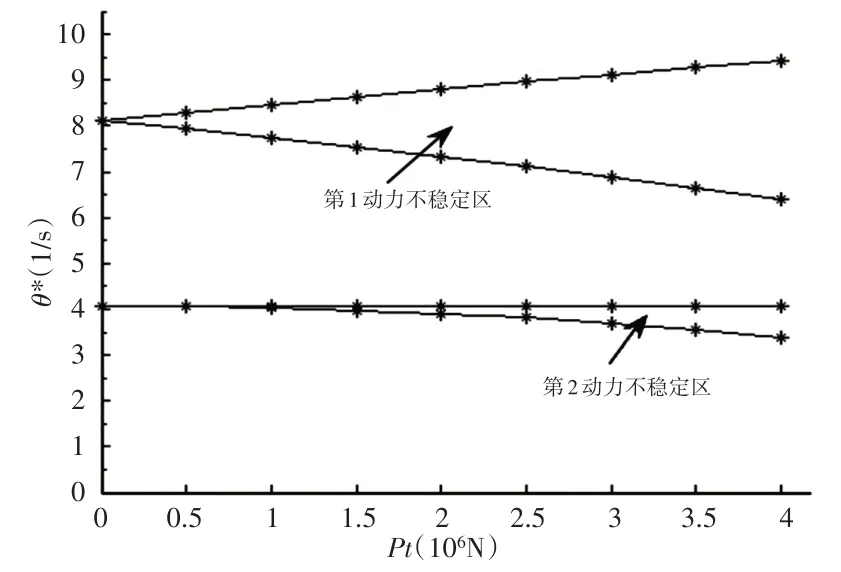
圖7 平面外動力穩定性曲線Fig.7 Out-of-Plane Dynamic Stability Curve

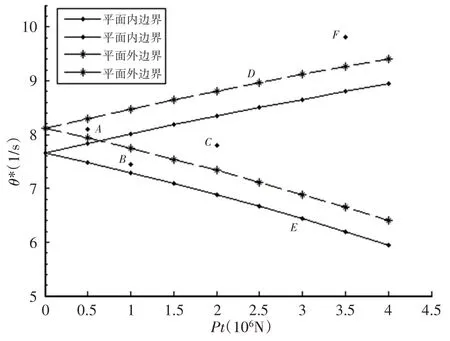
圖8 平面內和平面外動力不穩定區比較Fig.8 Comparison of In-Plane and Out-of-Plane Dynamic Instability Regions

使用Newmark積分獲得圖8中A、B、C、D、E、F六個位置的動力學響應，以此來驗證結構的動力不穩定區域。這6個點的振動頻率和幅值，如表1所示。當阻尼為零時，平面內點A～F的動力響應，如圖9～圖14所示。

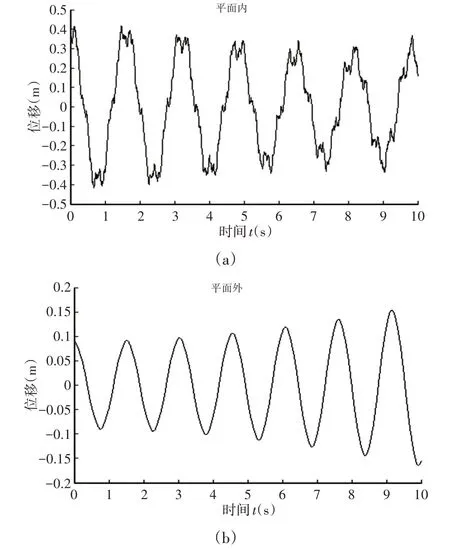
圖9 A點平面內和平面外的動力響應Fig.9 Dynamic Response in and out of Plane A

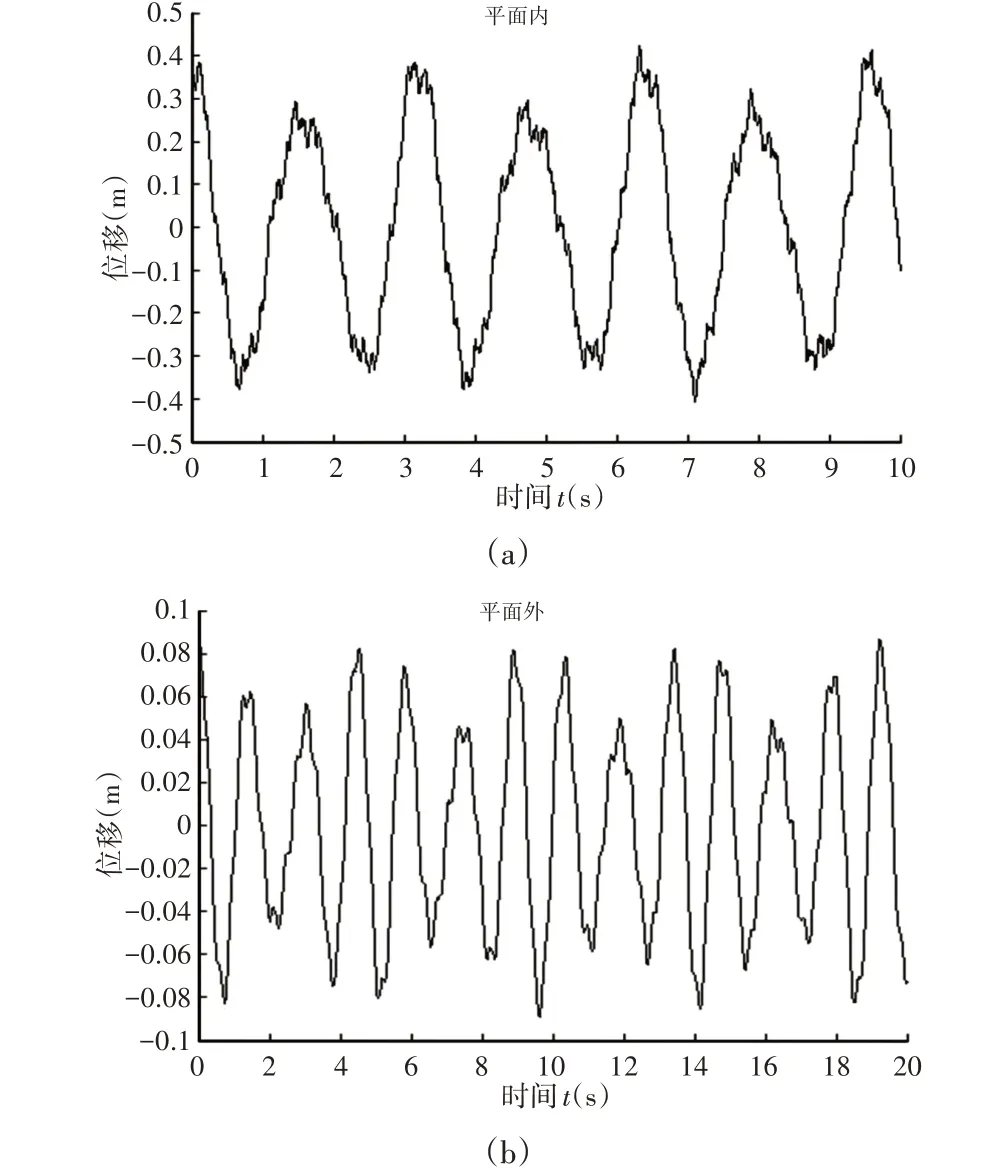
圖14 F點平面內和平面外的動力響應Fig.14 Dynamic Response in and out of Plane F

表1 A～F 6個點的振動幅值和頻率Tab.1 Vibration Amplitude and Frequency of 6 Points from A to F

由圖9可以看出，A點在平面內是有限位移的穩定振動，在平面外振動幅值隨時間的增長逐漸增大，所以A點在平面內是穩定的，在平面外是不穩定的；由圖10看出，B點在平面內是不穩定的，在平面外是由頻率不同但振動幅值相差很小的兩個簡諧振動合成的，是穩定的；由圖11看出，C點在平面內外的振動幅值均隨時間成指數增長，是不穩定的；由圖12看出，D點在平面內是穩定的，在平面外振幅由相對穩定逐漸減小，因此在平面外處于動力穩定和不穩定區的邊界上。

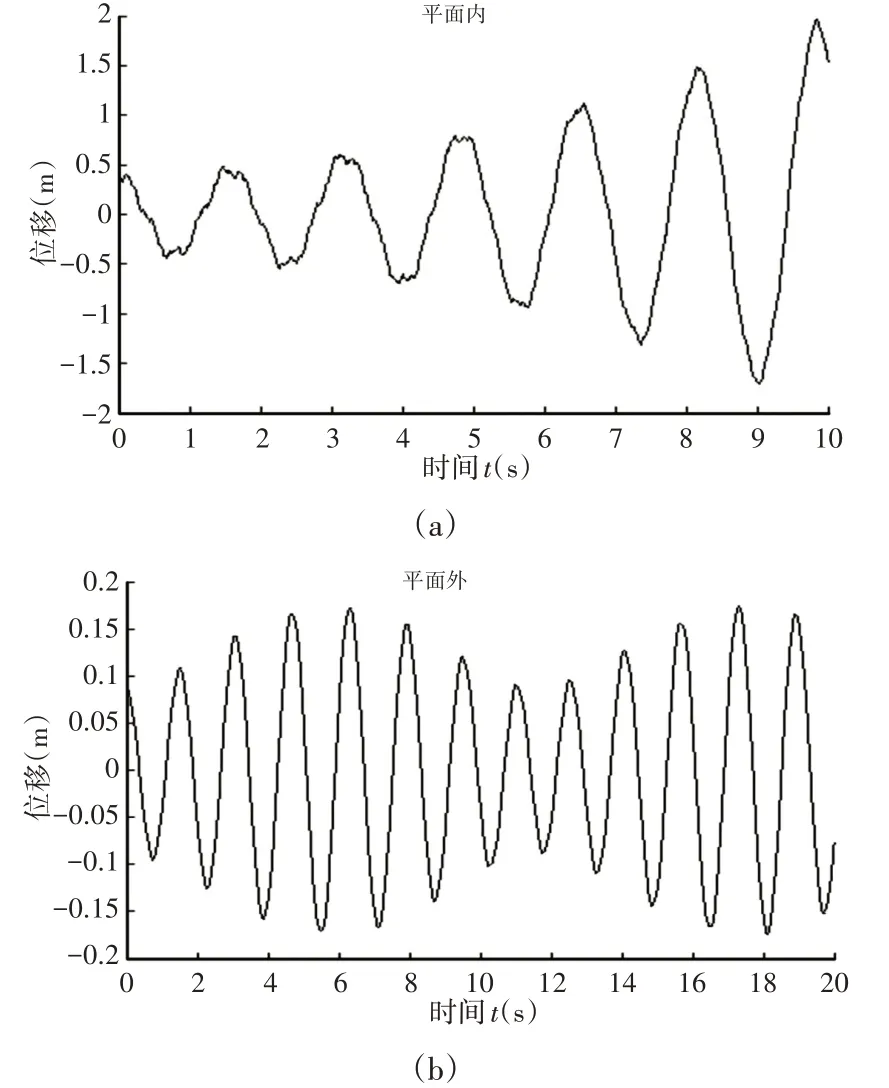
圖10 B點平面內和平面外的動力響應Fig.10 Dynamic Response in and out of Plane B

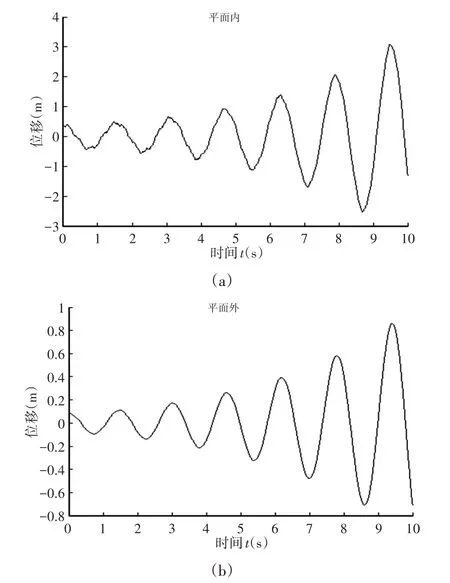
圖11 C點平面內和平面外的動力響應Fig.11 Dynamic Response in and out of Plane C

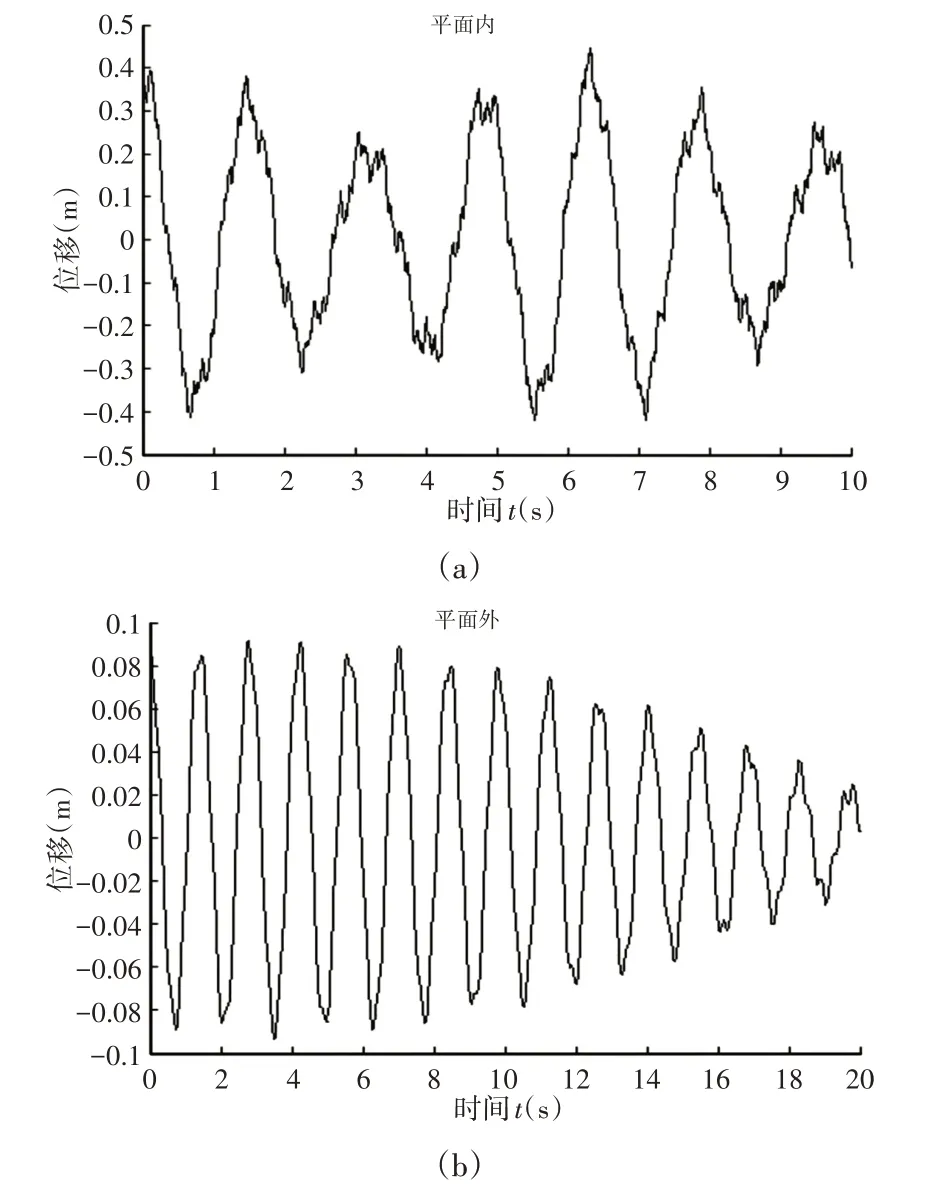
圖12 D點平面內和平面外的動力響應Fig.12 Dynamic Response in and out of Plane D

由圖13看出，E點與F點的情況正好相反，E點在平面內處于動力穩定和不穩定區邊界上，在平面外是穩定的；由圖14看出，在平面內外，F點均為穩定的；由上述結論可以得出，結構在平面內和平面外的穩定情況是不完全相同的，為了安全施工，應同時考慮平面內和平面外的穩定性。當存在阻尼時，動力不穩定區發生改變，如圖15所示。將平面外有阻尼和無阻尼的第一動力不穩定區比較，可以看出虛線部分（阻尼為0.2）的面積小于實線部分（無阻尼）的面積，說明阻尼使動力不穩定區的面積減小即系統更穩定。

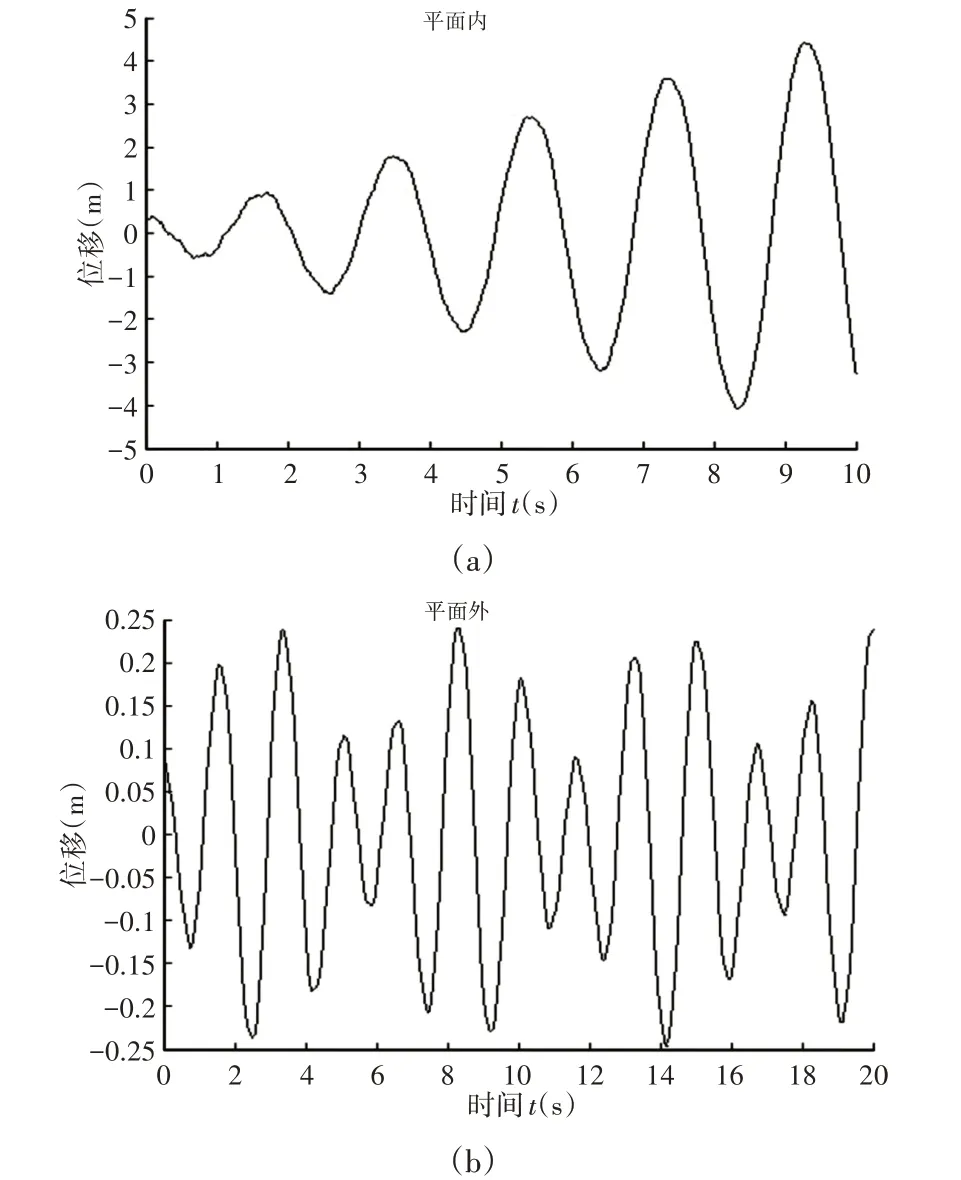
圖13 E點平面內和平面外的動力響應Fig.13 Dynamic Response in and out of Plane E

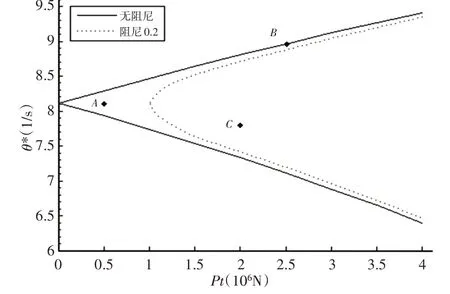
圖15 五節臂平面外第一動力不穩定區Fig.15 Five-Section Arm First Dynamic Instability Zone

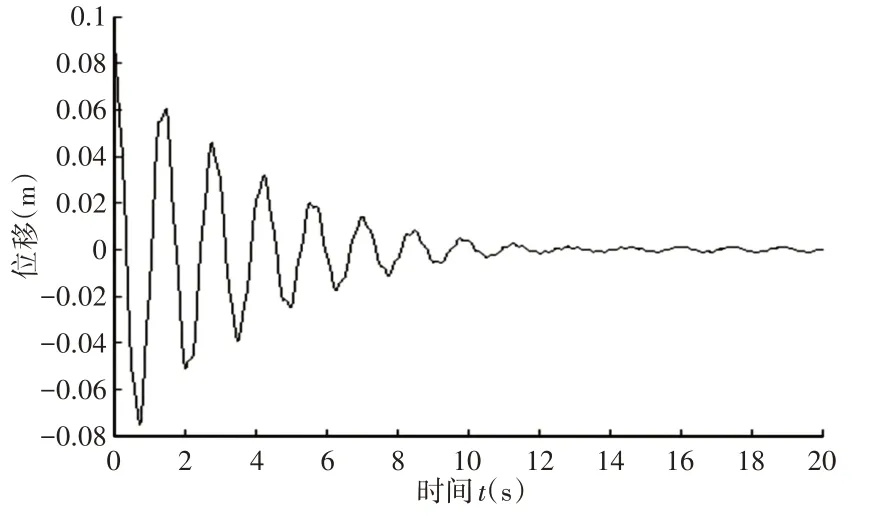
圖17 有阻尼B點動力響應Fig.17 Damped B-Point Dynamic Response

當阻尼為0.2時，對圖中3個點進行動力響應分析，如圖16～圖18所示。對比發現，A，B兩點振動幅度隨時間減小最終趨于穩定，得出阻尼使A點由動力不穩定變為動力穩定狀態，B點從邊界變為穩定狀態，C點的動力穩定性沒有變化。由上述結論可以看出，阻尼的存在會改變動力不穩定區，使動力不穩定區域減小。

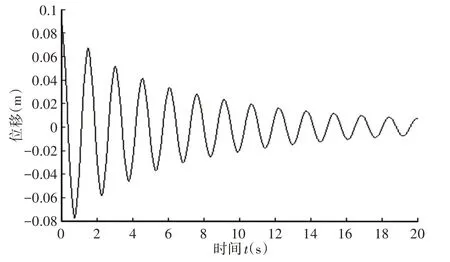
圖16 有阻尼A點動力響應Fig.16 Damped A-Point Dynamic Response

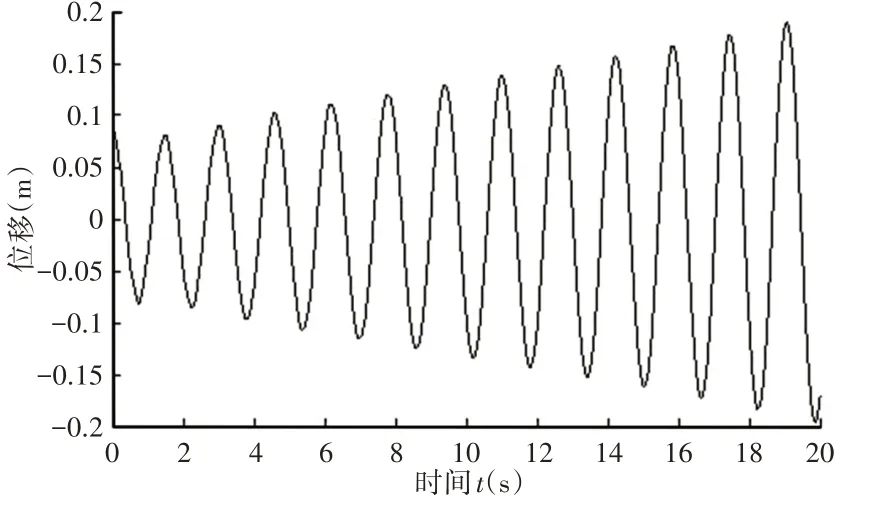
圖18 有阻尼C點動力響應Fig.18 Damped C-Point Dynamic Response

5 結論

（1）建立了計及變幅油缸作用下伸縮臂起升平面內和平面外參數振動分析模型，推導了起重機伸縮臂的參數振動方程和臨界頻率方程。

（2）以典型的五節起重機伸縮臂為例，繪制了伸縮臂動力穩定和不穩定區域，并取六點進行動力響應分析。分析結果表明：伸縮臂起升平面內和平面外可同時發生參數共振現象，平面外的臨界頻率略高于平面內的臨界頻率。6個特殊點的動力學響應結果表明，伸縮臂參數振動分析的結果是正確的。

（3）通過分析阻尼對伸縮臂動力穩定性的影響可知，阻尼的存在能減小動力不穩定區域，且在振動幅值Pt較小的情況下伸縮臂不會出現參數共振現象。